基于Zernike矩和熵的图像感知哈希算法

张大兴，陈娟娟，邵伯仲

(杭州电子科技大学 计算机学院，浙江 杭州310018)

图像感知哈希是基于图像内容的哈希算法，是一种由内容信息到感知摘要的单向映射［1］。图像感知哈希在基于内容的检索、内容篡改认证、数字水印、模式识别等领域有广泛的应用。图像感知哈希的研究得到学术界的重视，出现了如NMF［2］、R＆ASCH［3］、RIFJLT［4］等具有重要影响的代表性算法。

区别于传统密码学的哈希算法，图像感知哈希更强调针对图像内容，而不是图像数据进行哈希。简单地说就是内容相似的图像产生相似的哈希，内容不同的图像产生不同的哈希。本文利用Zernike矩的相位作为角度参考，利用熵作为图像特征来构建新型感知哈希算法。实验结果表明，该算法对不同图像具有较好的区分度，同时对加性噪声、JEPG压缩、旋转等常规操作具有较好的稳健性。

1 Zernike矩和图像熵

1.1 Zernike矩

Zernike矩是一组定义在单位圆x2+y2=1上的复数函数集{Vpq(x，y)}，Zernike多项式定义如式(1)所示［5－6］

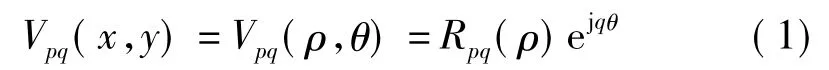
其中，ρ为点(x，y)到原点的矢量长度;θ为矢量ρ与x轴逆时针方向的夹角;Rpq为实直径多项式，其定义如式(2)所示

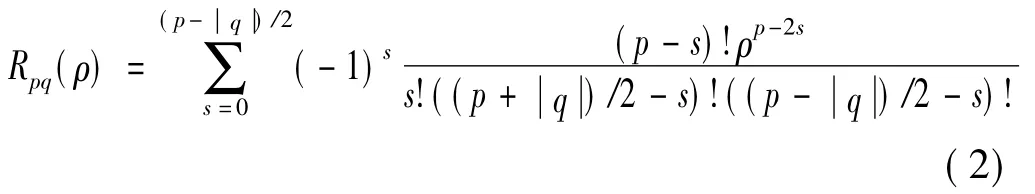
对于离散的数字图像来说，Zernike矩［6］的定义如式(3)所示，x2+y2≤1

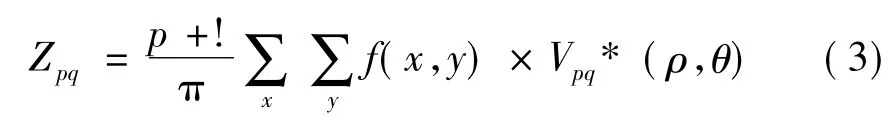
Zernike矩的相位具有旋转不变性，利用这个不变性可构建归一化的参考角度。

1.2 图像熵

图像熵表示图像灰度级集合的比特平均数，描述了图像信息源的平均信息量。熵的定义如式(4)所示

式中，E为输入的图像;ei表示像素值;p(ei)表示像素值为ei在图像中出现的概率。对于灰度图像，则N的取值为256。

2 哈希算法的过程

2.1 预处理

首先，将图像用双线性插值法归一化到256×256。然后计算归一化后图像的Zernike矩，从而得到相位角度作为图像的参考角度。在本文中，将图像旋转多个角度后，取相位的平均值作为参考角度，目的是使相位角更稳定。

2.2 环状分割和扇形分割

按等面积环块和等角度扇形块对图像进行分区［7］是产生哈希序列常用的两种方法。图1表示以图像中心为原点，将图像分割成径向等面积的环块。图2是以图像中心为原点，将图像分割成等角度扇形块。本文的哈希算法通过在半径方向划分环和角度方向划分扇形块将归一化后图像各均分为64等份。

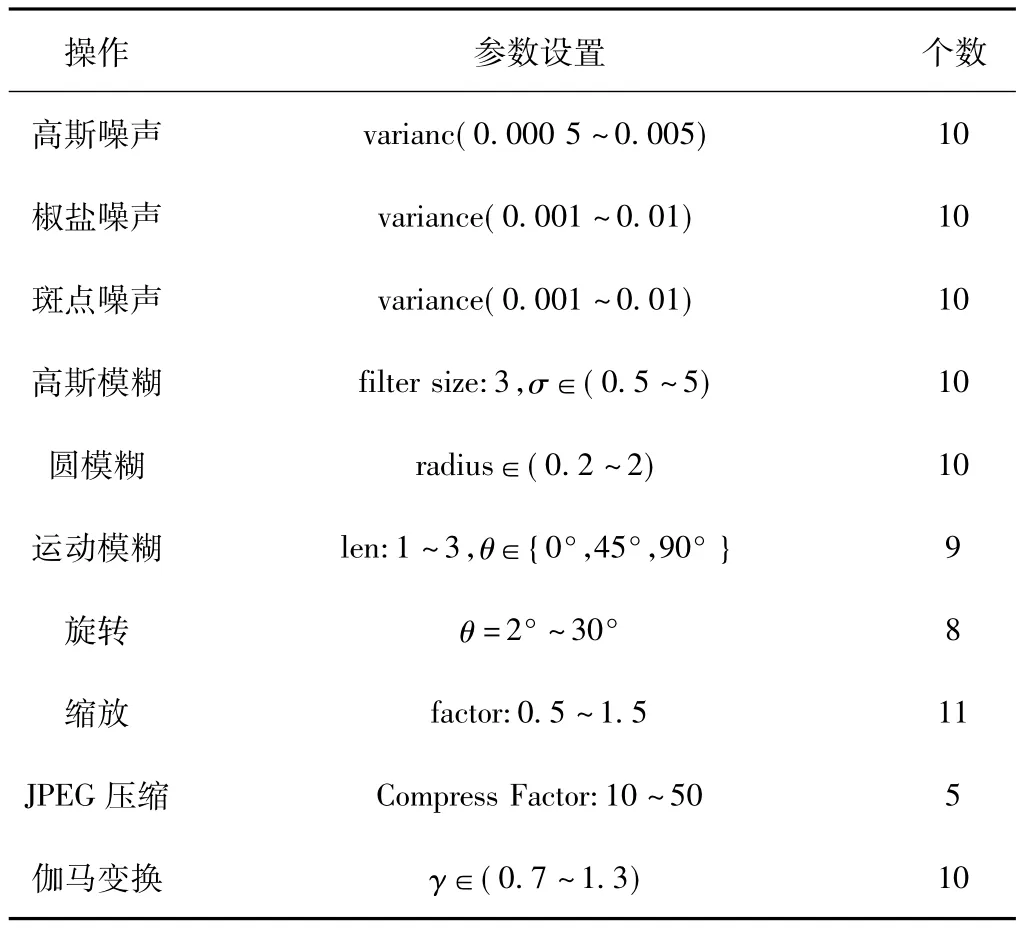
表1 内容保持类操作及参数

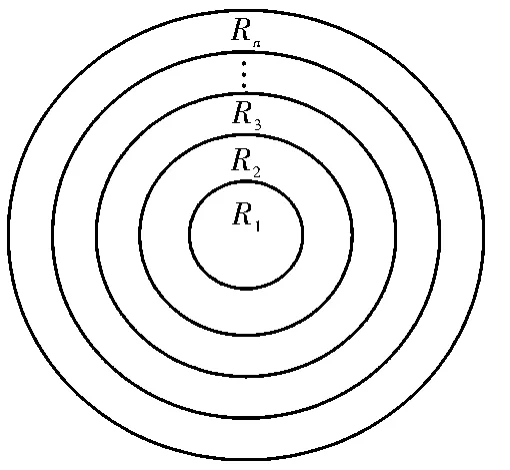
图1 等面积划分环块

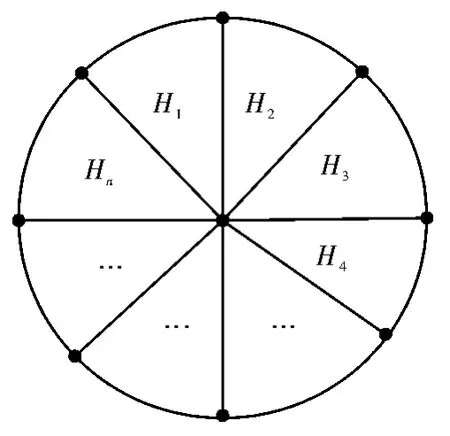
图2 等角度划分扇形块

2.3 熵的提取

取平均值后的Zernike相位角在本文中被用作等角度划分的起始位置，设计意图在于保持旋转的稳健性。计算每个环块和扇形块内的熵值，即hl=H(Rl)，l=1，2，3，…，n，作为图像内容的特征来生成感知哈希。

2.4 哈希序列的欧氏距离

将环块和扇形块的熵值进行串接，最后得到长度为128的哈希序列。通过计算两幅图像哈希序列之间的欧氏距离来判定图像内容的相似性。欧氏距离计算公式为

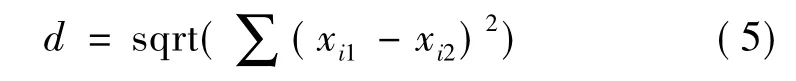
在此i=1，2，…，n，xi1表示第一个点的第i维坐标，xi2表示第二个点的第i维坐标。用欧氏距离来衡量图像内容的相似程度，要求和人类视觉的主观感知相一致:即人眼感知两幅图像越相似，得到的欧氏距离值就越小。

3 区分度和鲁棒性

本文主要从区分度和鲁棒性两个方面对这个哈希算法进行性能测试。本文算法所用的测试样本来自麻省理工学院媒体实验室的公开测试图库。通过大量的数据实验，选取欧氏距离4.5作为判定阈值。在该阈值下，算法的综合区分度达到94.1%。

鲁棒性检测是在保持感知内容不变的前提下，算法对常规有损操作的稳健性。本文的测试项目包括噪声、模糊、几何变换和压缩等。具体参数如表1所示，各项实验结果如表2所示，算法对常规有损操作有较好的稳健性。

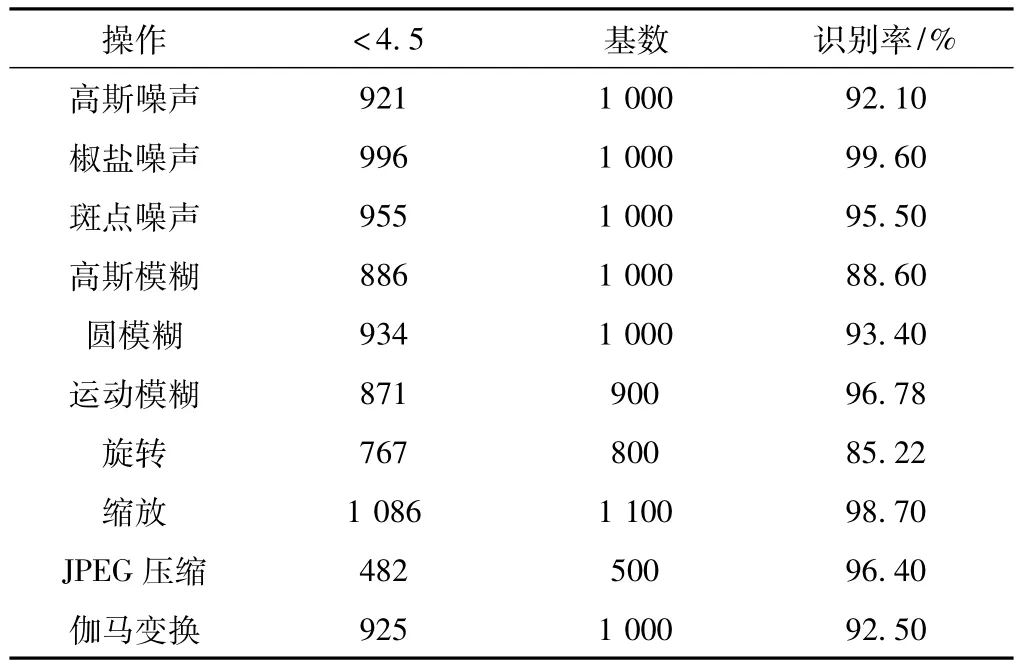
表2 对内容保持类操作的识别率

图3是将内容保持类操作结果图与其他样本图的欧氏距离放在一起的实验结果。图中包含12个样本图像与其他样本图像的欧氏距离，以及100个样本图像与各自10种内容保持类操作结果图的欧氏距离。所用到的内容保持类操作的参数分别为:高斯噪声0.000 6;椒盐噪声0.005;斑点噪声0.005;高斯模糊size=3 sigma=0.5;圆模糊radius=0.6;斑点模糊theta=45;旋转r=20;压缩QF=30;缩放s=0.8;伽马变换gamma=1.1。从图3可看出，不同图像的哈希值的欧氏距离多数大于阈值4.5，而内容保持类的近似图像的哈希值的欧氏距离基本均小于阈值4.5。

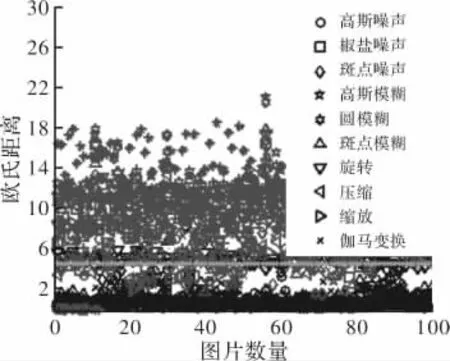
图3 图像之间的欧氏距离

4 ROC曲线

为进一步更直观地展示实验数据，用ROC曲线来展示各种操作下算法性能。ROC曲线横轴表示错误的接受率，即原本不是相同的图像而被识别为相同图像的概率。纵轴表示正确的识别率，即原本就是相同的图像也被正确地识别是相同的图像的概率。

图4是加噪后的ROC曲线图;图5是模糊操作后的ROC曲线图;图6是旋转、缩放、JPEG压缩、伽马变换的ROC曲线图。数据表明算法具有较好的整体性能。

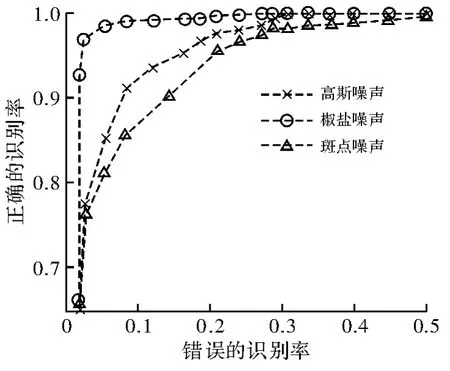
图4 加噪的ROC曲线

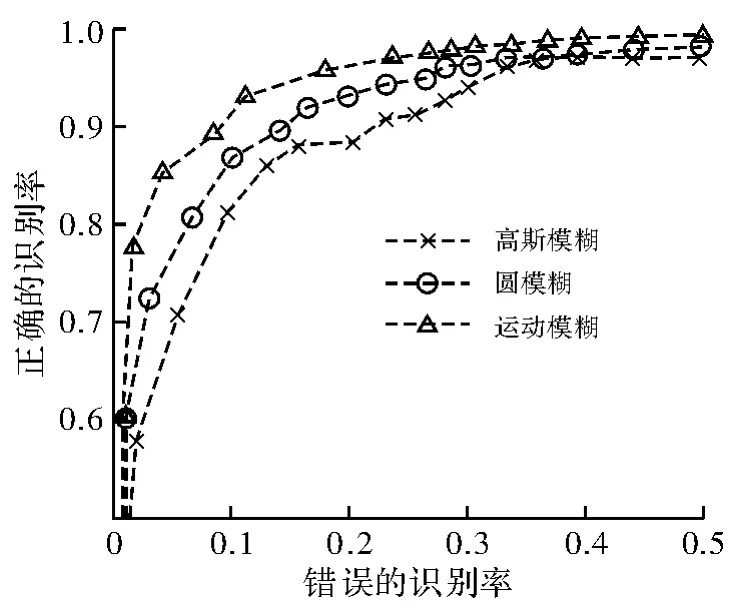
图5 模糊操作的ROC曲线

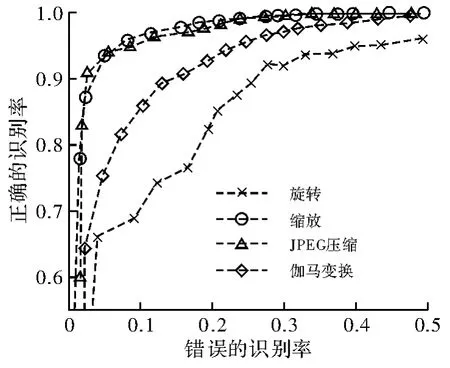
图6 旋转等操作的ROC曲线

5 算法对比分析

本文选择NMF［2］和R＆ASCH［3］这两个经典算法进行比较。NMF算法是基于非负矩阵分解的算法，对压缩、滤波等操作对其他算法有明显优势，但对旋转较敏感;R＆ASCH利用SIFT特征构造哈希，将图像进行等半径环状分割和等角度间隔区域分割，环状数和角度数均为10，和本算法分块划分上具有相似性。实验结果如表3所示(R＆ASCH算法数据直接采用原文数据［3］)。从实验数据可见，NMF算法整体表现优秀，但对旋转较为敏感，对伽马变换适应性较差。R＆ASCH算法与本文算法整体性能相似，但该算法计算复杂，难以满足大尺度图像在速度上的要求。

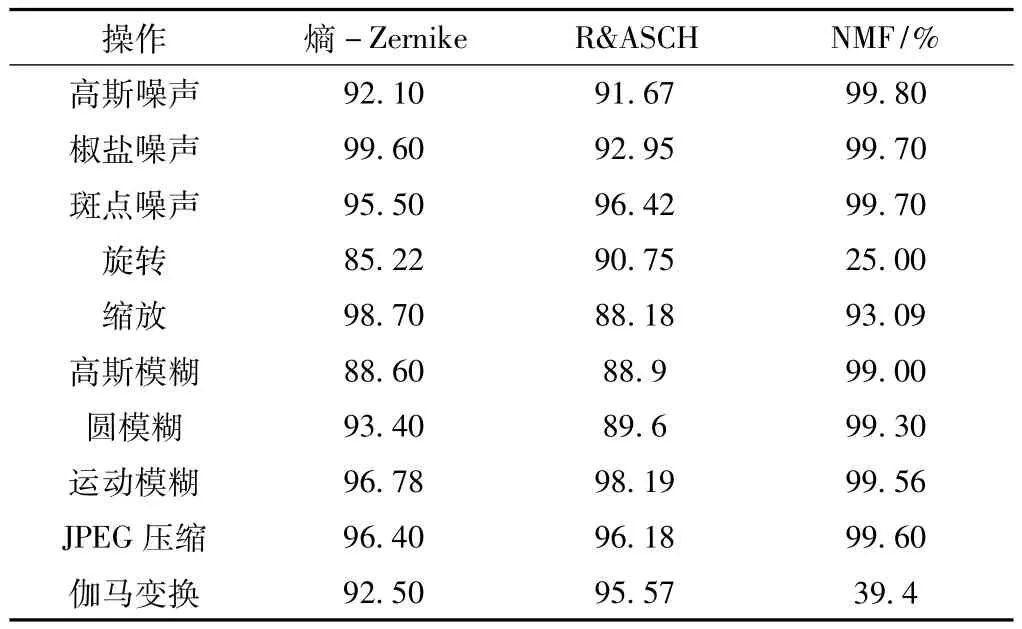
表3 算法对比

6 结束语

图像感知哈希技术应用广泛，本文提出了基于Zernike矩和熵的哈希算法。实验表明，算法兼具常规操作的稳健性和图像内容的区分能力。本文算法相比NMF、R＆ASCH等经典算法具有自身的优势。

［1］ 牛夏牧，焦玉华.感知哈希综述［J］.电子学报，2008，36(7):1405－1411.

［2］Monga V，Mhcak M.Robust and secure image hashing via non－negative matrix factorizations［J］.IEEE Transactions Information Forensics and Security，2007，2(3):376－390.

［3］Lv X，Wang Z J.Perceptual image hashing based on shape contexts and local feature points［J］.IEEE Transactions on Information Forensics and Security，2012(3):1081－1093.

［4］Lv X，Wang Z J.An extended image hashing concept:content based finger printing using FJLT［J］.Eurasip Journal of Information Security，2009(6):1－17.

［5］Hyung Shin Kim.Invariant image watermark using zernike moments［J］.IEEE Transactions on Circuits and Systems for Video Technology，2003，13(8):766－775.

［6］Zhao Y，Wang S，Zhang X，et al.Robust hashing for image authentication using zernike moments and local features［J］.IEEE Transactions on Information Forensics and Security，2013，8(1):55－63.

［7］Tang Z，Zhang X，Huang L，et al.Robust image hashing using ring－based entropies［J］.Signal Processing，2013，93(7):2061－2069.