一种基于二分法的LFM调制斜率估计算法

崔 刚，李 涛

(国防科学技术大学ATR国防重点实验室，湖南 长沙410073)

LFM信号在雷达、无线电通信、地质勘测与地震探测、生物医学成像、物理学、声呐等领域都有着广泛应用［1－4］。作为电子侦查的重要环节，需要对LFM信号的参数进行估计，调制斜率是LFM信号中较为关键的一个参数。对LFM信号估计的主要方法包括解线调、Radon－Wigner变换［0］和分数阶傅里叶变换［0］、最大似然估计(MLE)［0］等方法。其中，最大似然估计具有较高的精度，其估计精度接近卡拉美罗下界，但由于这种方法需进行二维联合搜索，运算量大，不利于实时处理。Radon－Wigner变换方法相对于最大似然估计的方法，减少了大部分的运算量，但由于这种方法算法较为复杂，在具体实现中存在较大难度。通过解线调的方法估计LFM信号的调制斜率能获得较高的精度［0］，但精度受制于试解线条的步进，步进选择过大，无法达到要求的精度，步进选择过小，则搜索的次数相应的增加，不利于算法的实时实现，本文通过对自相关方法解线调误差的分析，在合理的区间范围内使用基于二分法的估计方法，获得了较高的精确度和较快的处理速率。

1 自相关参数估计方法

通过延迟自相关方法得到的调制斜率的框图如图1所示。

图1 自相法框图

输入信号经过一定时间延迟后与原输入信号进行相关运算，通过低通滤波器后得到窄带正弦信号，通过估计该信号的频率，进而得到LFM信号的调制斜率。

LFM信号的一般表达式为

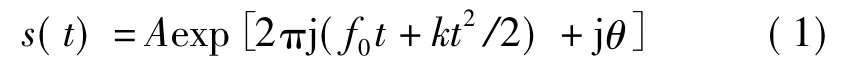
式中，A为LFM信号的幅度;f0是初始相位k为调制斜率;θ为初始相位。

接收信号是叠加了加性高斯白噪声的信号

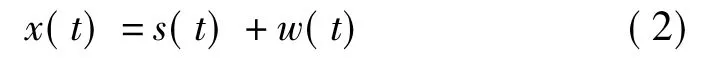
其中，w(t)是高斯白噪声;x(t)是接收到的信号。对信号延迟τ，并与原始信号做自相关，得到的信号为

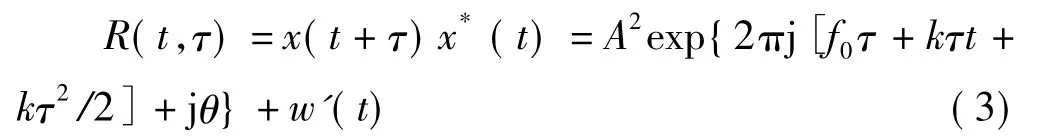
可见，若固定τ，经过相关后的信号为单频正弦波信号。提到的方法对正弦信号频率进行估计，若正弦信号频率的估计值为，则调制斜率k的估计值。

对自相关后的信号产生的噪声进行分析，则有

假设原噪声功率为e2，则此时的噪声功率为

若输入信号的信噪比SNRin，则输出信号信噪比可写作

由文献［0］可知，为了得到最优的估计结果，延迟为信号持续宽度的0.4倍，此时调制斜率估计的克拉美罗下限为［0］

其中，N为信号的采样数;Δt为采样间隔，文献［0］同时证明，实际计算的信号的均方误差不超过克拉美罗下限的两倍，下面的算法根据这一结果选择试解调的频率范围。

2 试解调原理

对式(1)计算信号的功率，有能量定理

对于LFM信号，具有近似矩形的幅频特性，若信号带宽为B，且B=kT，频谱的幅度均值为式(8)可简化为

可见，当信号的能量固定时，信号的带宽与信号的幅度值呈反比。若构造信号g(t)=exp(－jπktet2)与s(t)相乘，可得

由式(9)和式(10)可知，kte与k越接近，信号的带宽越小，则对应的信号功率均值越大。若以一定的步进对整个可能的调制斜率进行扫描，则可得到较为精确的信号调制斜率，传统的试解调算法流程如表1所示。

表1 传统试解调法流程

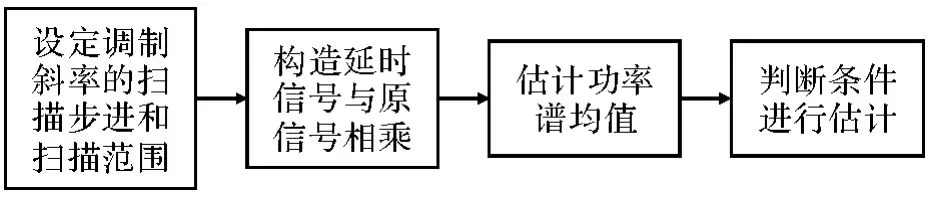
图2 传统试解调流程图

3 二分法试解调算法

传统试解线调流程存在比较明显的缺陷，当搜索范围较大时，需进行大量的试解调的运算，且由于对调制斜率没有先验信息，会造成由于噪声污染，出现局部的大值，产生误判。

为解决这一问题，考虑第二节描述的方法。首先，通过自相关的方法，计算出调制斜率的粗略估计值，根据文献［0］给出的计算结果，选择两倍的卡拉美罗限2D()作为统计的估计均方误差上限，由3σ理论，搜索范围可被限定在［－6D()，+6D()］区间内。

为进一步降低搜索的次数，使用二分法对区间进行搜索，首先，选择－6D()、+6D()分别按照式(3)计算相乘以后的信号，并分别计算信号的频谱均值，若左端点的频谱均值大于右端点的频谱均值，则实际的调制斜率在左半区间，反之，调制斜率在右半区间，重复上述过程，直到达到要求的精度为止。

表2 基于二分法的试解调算法

图3 基于二分法的试解调算法

4 仿真验证

为了验证算法的有效性和实时性，分别对传统的试解调算法和本文提到的算法进行了仿真，仿真环境酷睿双核2.4 GHz CPU，Windows7 SP1操作系统，2 GB内存，Matlab 2012a版本。构造的线性调频信号起始频率100 MHz，带宽50 MHz，采样频率100 MHz，信号时长4μs，在信噪比－10～10 dB的条件下各进行了1 000次蒙特卡洛仿真，其中估计精度误差要求≤1 000。

为了验证算法的实时性和可靠性，比较了自相关方法，传统试解调方法，本法所述方法在不同信噪比下的运行时间和估计正确率。

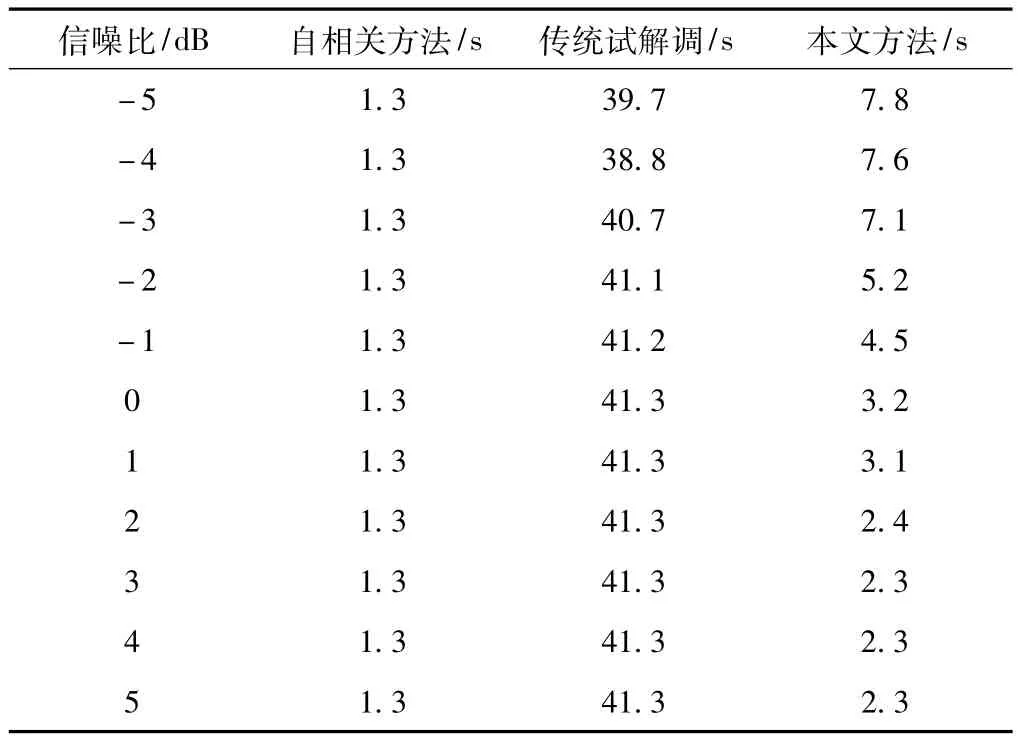
表3 几种算法运行时间对比

图4 3种算法时间对比

表4 几种算法正确率对比

图5 几种算法正确率对比

从表3可看出，本文方法相比于传统的试解调算法具备更快的运行速度，从表4可看出，本文方法比传统试解调算法具备更好的性能，从表3发现一个反常现象，在信噪比较低时，传统算法的运行时间反而较少，这是因由于噪声的影响，可能在真实的估计频率之前就已出现了算法结束的条件，于是停止搜索，联合表3和表4可发现，出现搜索时间短的情况下，正确率均不是100%。比较表4中两种算法的正确率可发现，本文方法的性能优于传统试解调算法，通过自相关法大致确定了范围，使得发生错误的概率减小。综合两个表所列出的实验结果，可证明本文算法具备更好的实时性和有效性。

5 结束语

本文通过将自相关算法和试解调结合，提出了一种基于二分法的LFM信号调频斜率估计方法，与传统的试解调算法相比，具备更优的估计性能和更快的运算效率，为工程化的精确估计线性调频信号调制斜率提供了参考。

［1］ 李尧辉.噪声环境下线性调频信号参数估计技术研究［D］.广州:华南理工大学，2013.

［2］ 牛萌，李钊，朱晓光，等.LFM信号参数估计的最大似然改进算法［J］.无线电通信技术，2009，35(3):59－61.

［3］ 张容权，杜雨洺，杨建宇，等.一种LFM信号最大似然估计模型与参数估计快速算法［J］.电波科学学报，2005，20(5):651－655.

［4］ 胥嘉佳，刘渝，邓振淼.LFM信号参数估计的牛顿迭代方法初始值研究［J］.电子学报，2009，37(3):598－602.

［5］Raveh I，Mendlovic D.New properties of the radon transform of the cross wigner/ambiguity distribution function［J］.IEEE Transactions on Signal Processing，1999，47(7):2077－2080.

［6］Xia X G.Discrete chirp－fourier transform and its application to chirp rate estimation［J］.IEEE Transactions on Signal Processing，2000，48(11):3122－3133.

［7］Abatzoglou T J.Fast maximum likelihood joint estimation of frequency and frequency rate［J］.IEEE Transactions on Aerosp Electronic System，1986，AES－22(6):708－715.

［8］ 张华.低信噪比下线性调频信号的检测与参量估计研究［D］.成都:电子科技大学，2004.

［9］Rife D C，Boorstyn，Robert R.Single tone parameter estimation from discrete－time observations［J］.IEEE Transactions on Information Theory，1974(20):1918－1927.

［10］刘渝.快速解线性调频技术［J］.数据采集与处理，1999，14(2):175－178.