一种改进的基于舰船目标SAR图像的超分辨率方法

贾洪辰，于 勇，张 彬

（北京遥测技术研究所 北京 100076）

引 言

在对舰船目标进行SAR成像的实际项目与工程应用中，常常需要考虑大斜视、前视等极端情况，此时SAR图像的分辨率难以得到保证。为达到目标识别和精确定位的目的，SAR图像的分辨率需要达到一定的精度，因此提高SAR图像分辨率是实际工程应用中的一项重要任务。

关于SAR图像的超分辨率技术国内外学者已提出多种算法，主要有正则化方法、稀疏表示方法等。1985年，Poggio T等[1]在Nature上撰文阐述图像处理正则化方法的有关理论后，随着对图像超分辨率问题的研究，该方法逐渐成为SAR图像超分辨率技术的主要方法之一。稀疏表示法与近些年来兴起的压缩感知理论有着密切联系，已相继出现了一批优秀的图像稀疏表示工具，如离散余弦变换（DCT）、小波变换（WT）、曲波变换（curvelet）和复数小波（complex wavelet）等[2～4]。这些图像表示工具的相同之处在于，利用变换域中少量显著非零的系数来表示图像，实现图像的稀疏表示。

现有的超分辨率方法在实际应用中存在一些问题，例如，正则化方法对于点目标密集的图像处理结果较差，稀疏表示法得到的结果杂波较多并且对噪声的抑制较差。本文通过研究现有SAR图像超分辨率方法之间的联系，基于舰船目标的模型特点，提出一种基于Fourier字典的稀疏表示方法与正则化方法结合使用的SAR图像超分辨率方法。首先通过理论分析证明了该方法可以有效地解决现有方法在提高舰船目标SAR图像分辨率应用中存在的问题，然后分别对点目标和舰船目标的SAR图像仿真数据进行处理，验证了本文方法提高舰船目标SAR图像分辨率的可行性。

1 舰船目标的先验信息及模型

由于目标对入射波的调制，雷达接收的散射电磁波具有不同于雷达发射的电磁波的性质。这种因调制效应产生的电磁波差异是由目标本身的物理结构性质决定的，因此散射波中必然包含关于目标物理结构的信息。根据几何绕射理论，如果入射波的波长小于目标尺寸，那么目标的后向散射场可认为是由多个孤立散射中心组成，每个散射中心的散射场表示为[5]：

对于舰船目标，其背景是海面，雷达波束与海面的作用主要有两种——镜面反射和Bragg散射。当海面比较平静时，雷达波束与海面的作用主要是镜面反射，雷达几乎接收不到回波，即在SAR图像中，海面相对很暗；当海面风浪较大时，雷达波束与海面的作用主要为Bragg散射，即会产生较强的后向散射，这种散射主要是布拉格散射（布拉格散射是一种共振散射，入射电磁波与波长在其同一量级的海面波发生共振，此表面波称为布拉格波）[6]，此时雷达接收到的回波较强，SAR图像中海面呈现出较亮的像素点。

舰船主要由金属制成，对雷达波具有极强的后向散射能力，它在SAR图像上表现为几个乃至数十个像素的高亮度点目标。一般情况下，即使海面风浪很大，舰船目标的后向散射回波也要远远强于海杂波。因此，舰船目标的SAR成像模型可以认为是在较大海杂波背景下的密集点目标模型，这种模型对应于式（1）中的情况。

2 稀疏表示法与正则化法结合的超分辨率方法

SAR成像的理想点散射模型即基于几何绕射理论的目标模型中的情况。因此对于含有p个理想点散射中心的目标而言，在频率f和方位角φ观测下，目标后向散射场表示为：

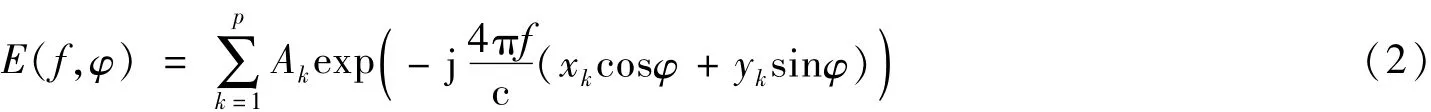
式中，Ak、（xk，yk）分别表示第k个散射中心的复振幅和在散射场中所处的位置坐标。如果将式（2）中的指数项看成一组基函数的话，那么在一定程度上可认为复振幅Ak是稀疏的。

令fx=fcosφ，fy=fsinφ，可得出SAR的相位历史域点散射模型：

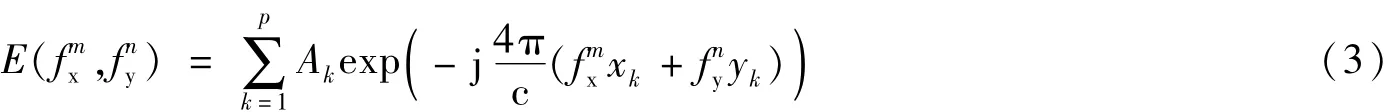
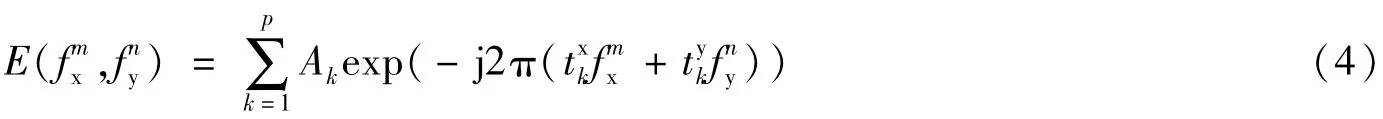
并且在直角频率域进行均匀采样，则有

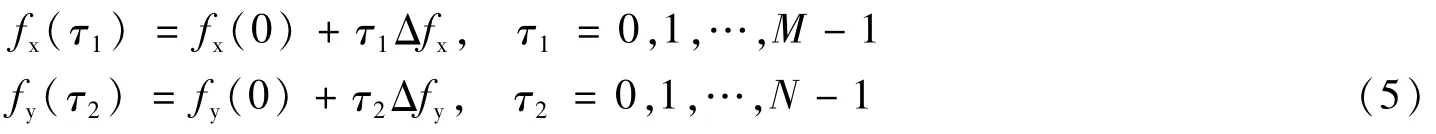
又

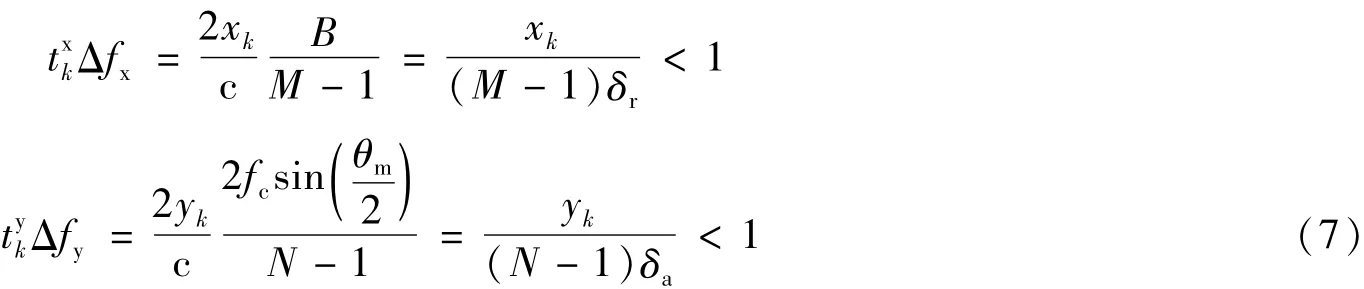
式中，δr和δa分别为距离向和方位向分辨率，由分辨率的定义容易得出和小于1。此时取

有

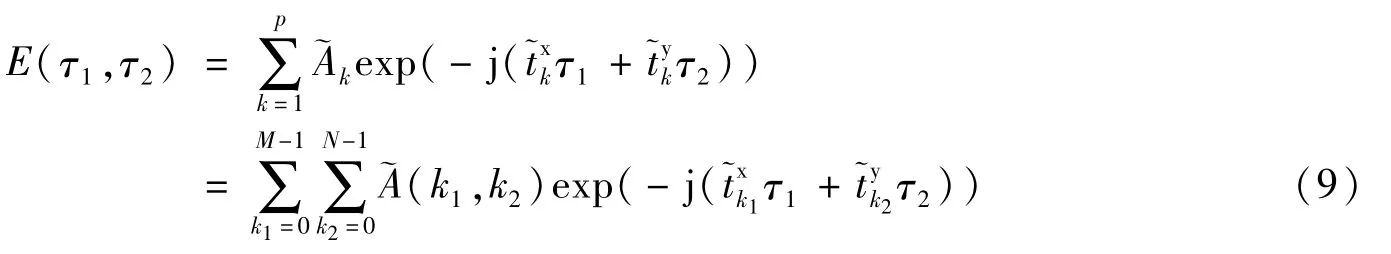
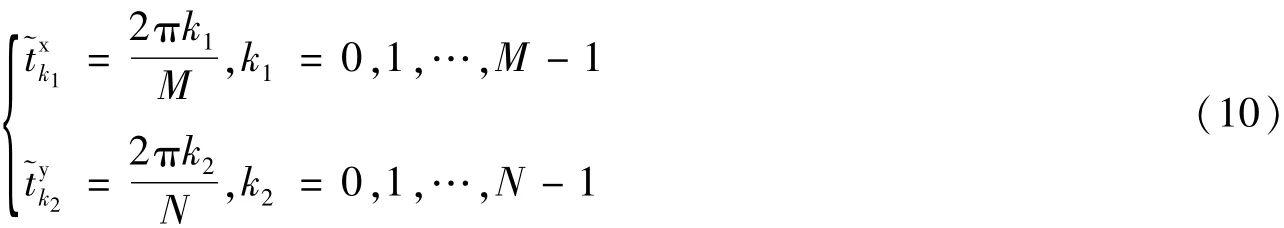
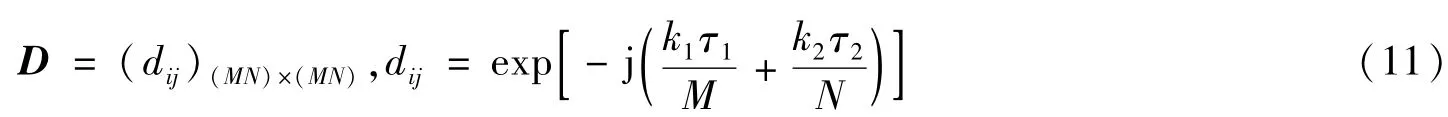
它实际上是标准的Fourier字典。对M×N网格进一步采样加密，即令

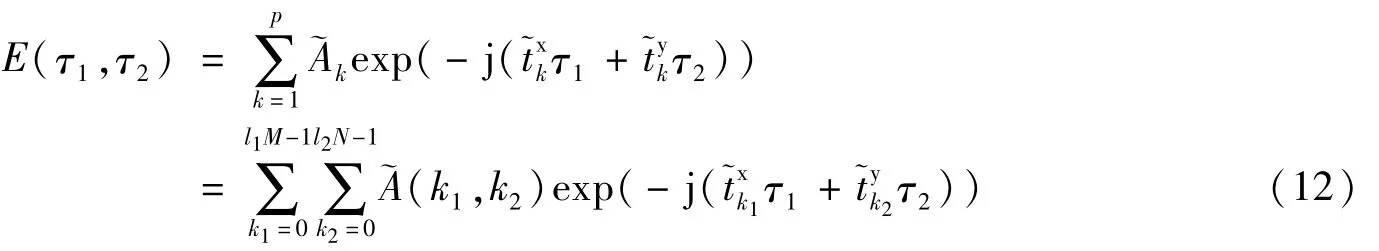
式中，l1、l2定义为超完备率，且有l1、l2大于1，此时做同样的采样，则参数网格取为（l1，l2）重超完备网格：

此时根据稀疏表示理论，可以取字典形式为：

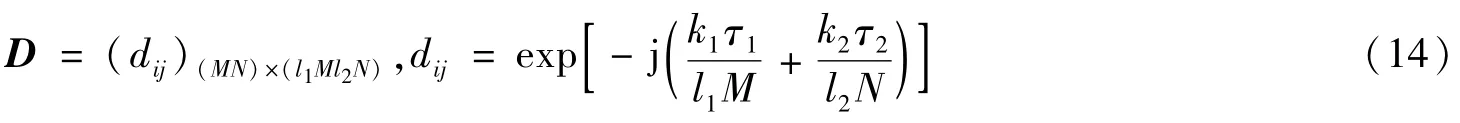
式（14）即是超完备的Fourier字典。SAR的超分辨率成像问题应采用超完备的Fourier字典。考虑到噪声，在超完备的 Fourier字典下，观测数据的分解形式为：

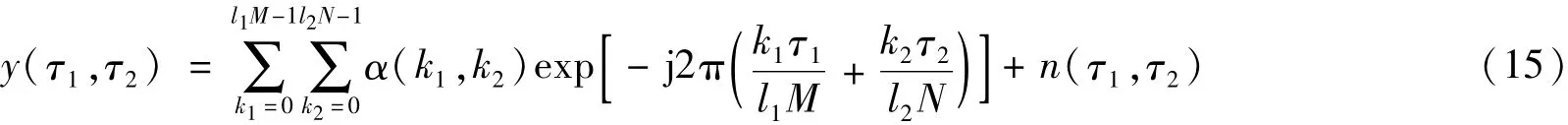
其中，α（k1，k2）为网格上各点的幅度矩阵，n（τ1，τ2）为噪声。这里先假设网格上每个点都为散射中心，当它确实是散射中心时，其对应的系数α（k1，k2）不为0，当它确实不是散射中心时，对应的系数α（k1，k2）为0。由舰船目标SAR图像的稀疏先验特性可知，矩阵α中只有少数元素不为零。求解超分辨率问题，就是由已知的y（τ1，τ2）求解α，即：

Donoho等人证明了在稀疏条件下式（16）和式（17）的等价性[7～9]。由Lagrange乘数法可将式（17）转化为求解下述复数域的最优化问题：

式中，λ为Lagrange参数，表示l2范数。对Fourier字典进行降阶可以大大减少运算量，具体过程如下：

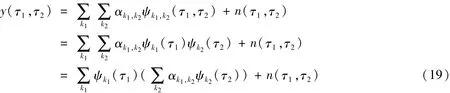
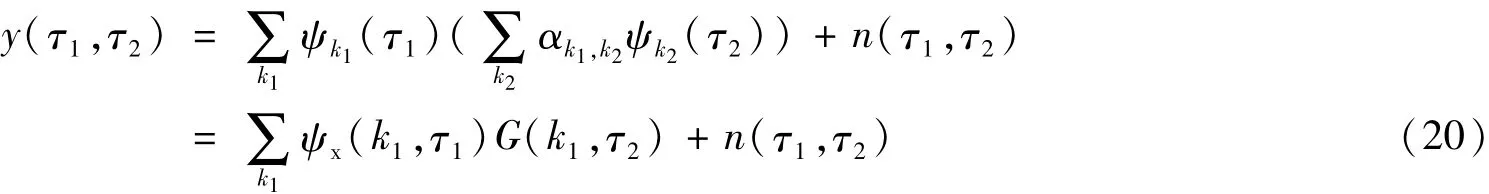
或

对于稀疏信号来说，α只有少数元素不为零，显然G=αψy的每一列也只有少数元素不为零，因此可以先构造行方向的字典，依据，对图像矩阵的每一列进行类似一维信号的基追踪处理，得到G；再构造列方向的字典，依据，对G的每一行进行类似一维信号的基追踪处理，即可得到α的估计值。

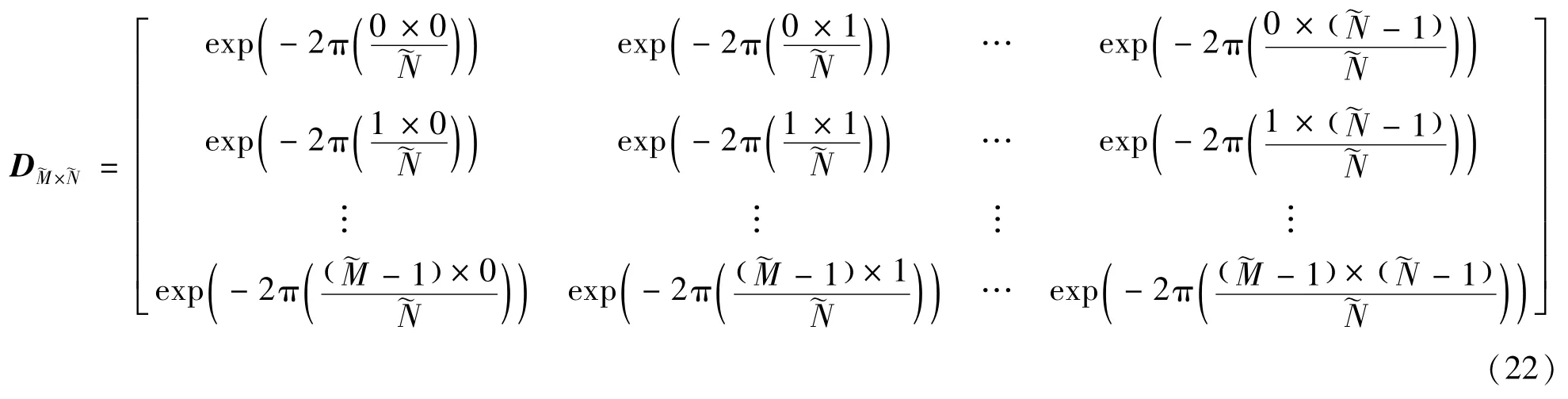
上述过程中，基追踪处理即求解式（18），可利用式（23）迭代求解：

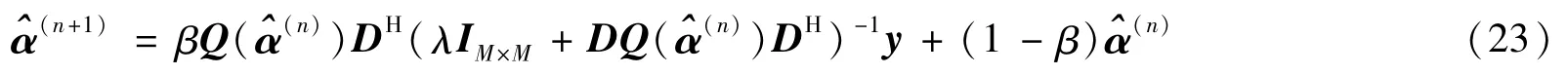
式中β为迭代步长，0＜β≤1，初值取，其中D+为D的广义逆矩阵。迭代的终止条件由控制，δCG为一足够小常数（这里可取δCG=10-3）。将得到的优化解代入中可得外推的相位历史数据，再进行IFFT变换即可得到高分辨率重构图像。

在上述处理过程中，式（18）中的λ取值较为困难，其大小代表了稀疏先验在约束条件中的重要性；λ值过小，会导致解的稀疏性较差，从而产生一些旁瓣和杂波，同时由于稀疏先验在约束条件中所占比例较小，使得结果对噪声的抑制能力较差；λ值过大，会导致迭代收敛很慢。因此，稀疏表示的结果可写成式（24）的矩阵形式。

式中，y为稀疏表示法得到的结果，f是场景真实散射系数，n1表示稀疏表示法残余的噪声，v表示稀疏表示法中产生的杂波和旁瓣，w=n1+v。显然，去除稀疏表示结果中的杂波、旁瓣以及残余噪声就是在已知y的情况下，利用SAR图像的稀疏先验信息，得到尽可能不失真的场景真实散射系数f，此问题可采用正则化方法进行处理。正则化方法可以对感兴趣的特征点进行增强，从而在一定程度上抑制旁瓣和杂波，同时使原SAR图像中的噪声得到一定程度的抑制。正则化方法的原理如下：

J（f）表达式的第一项称为数据逼近项，用于度量数据的逼近程度，第二项为正则化项，反映了对所采用先验信息的某种度量。超分辨率的结果依赖于使用的限制条件（先验信息），因而ψ（f）的选择非常重要。选择ψ（f）的一个主要原则是减少不希望出现的伪目标，同时增强有用的图像特征。

由于待处理的数据具有稀疏性特征，由稀疏表示原理可知表示目标真实信息的参数要尽量少，参数个数少的先验信息可以表示为min‖β‖0。l0范数不具有稳健性，对分析噪声污染信号不具有自适应能力。Donoho等提出采用较稳健的lk范数代替l0范数。这样SAR图像的超分辨率问题可以转化为如下的多目标优化问题：

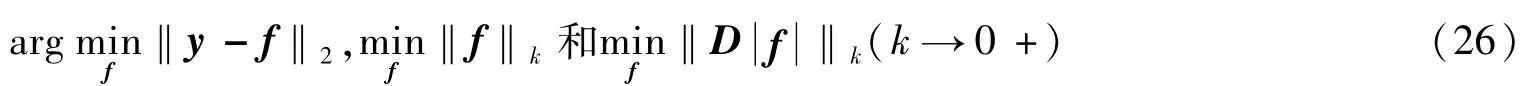
式中，D为二维微分算子（梯度）的离散近似，为复值向量的幅度向量。式（26）中第二项反映目标的稀疏先验，第三项反映目标边缘的稀疏先验。

如此便将SAR成像处理问题转化为求解式（27）的最优化问题[10]。

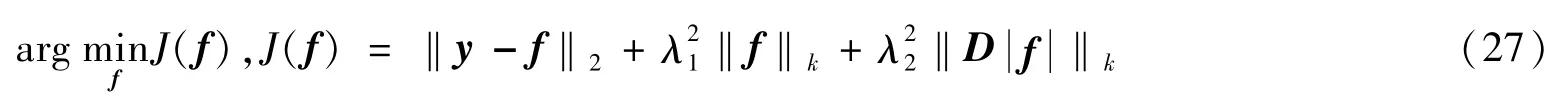
式中，λ1和λ2为正则化参数，其大小取决于两类特征（图像目标的点特征和图像的区域特征）的相对重要性，对于本文来说可以取λ2=0。关于f的最优化问题可通过Newton迭代算法求解，具体过程参见文献[10]，这里不再详述。

3 仿真及实测数据结果

为验证本文方法对SAR图像的超分辨率处理效果，分别对5个点目标和舰船目标的仿真图像进行处理。其中5个点目标是利用式（3）建立的，并且加入均方差为20的高斯白噪声，其振幅和坐标如下：

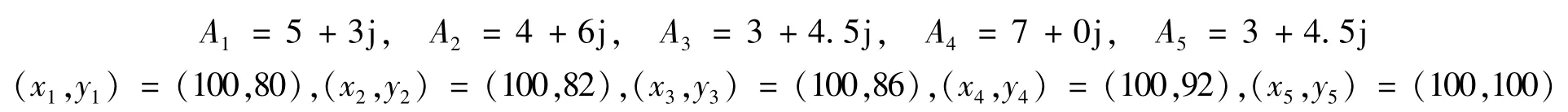
舰船目标的仿真图像是利用RD算法成像得到的，其仿真成像系统参数为：中心频率1×109Hz，带宽3 ×107Hz，脉冲持续时间5×10-6s。

分别利用正则化方法、稀疏表示法以及本文方法对点目标和舰船目标的仿真数据进行处理，结果如图1～图8所示，坐标单位为m。

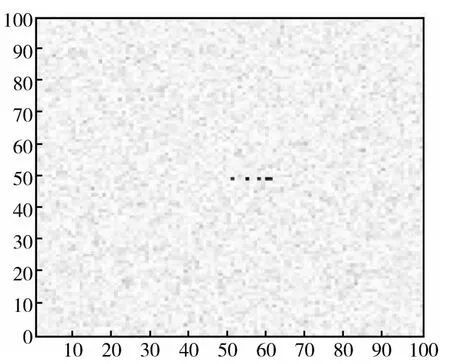
图1 点目标原图Fig.1 Point target

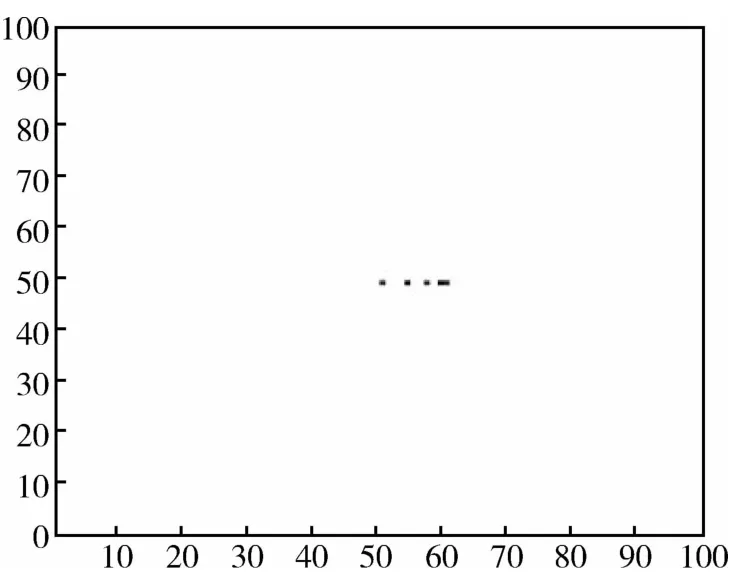
图2 点目标正则化结果Fig.2 The result of point target by the regularization method

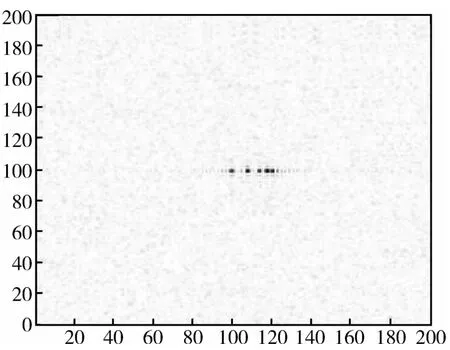
图3 点目标稀疏表示法结果Fig.3 The result of point target by the sparse representation method

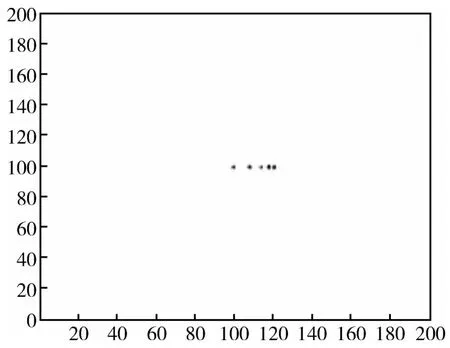
图4 点目标本文方法结果Fig.4 The result of point target by the proposed algorithm

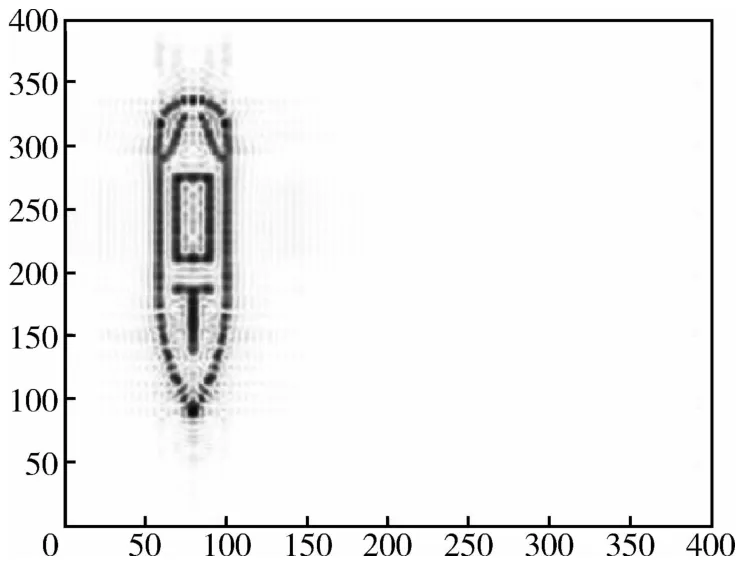
图5 舰船目标原图Fig.5 Ship target

图6 舰船目标正则化结果Fig.6 The result of ship target by the regularization method

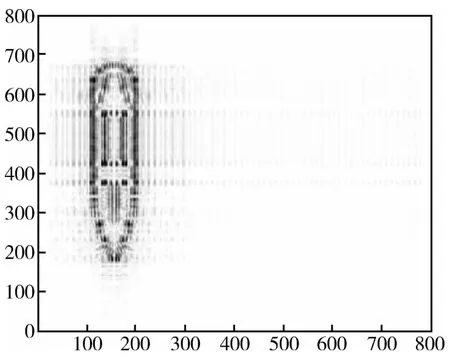
图7 舰船目标稀疏表示法结果Fig.7 The result of ship target by the sparse representation method

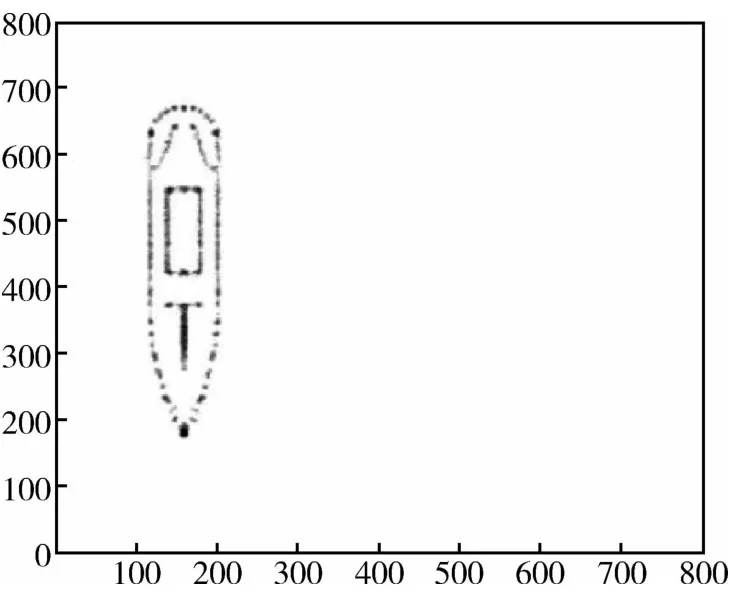
图8 舰船目标本文方法结果Fig.8 The result of ship target by the proposed algorithm

对比图1～图4，可得到以下结论：图2中，点目标经过正则化方法处理后，右面两个点目标不能区分开，但是噪声得到了有效抑制；图3中，点目标经过稀疏表示法处理后，虽然右面两个点目标得以区分开，但是杂波及噪声依然很明显；图4中，点目标经过本文方法处理后，右面两个点目标得以区分开，并且杂波和噪声得到了抑制。通过对比结果可以看出，正则化方法可以有效抑制图像中的噪声和杂波，但是不能有效地区分密集的点目标；稀疏表示法虽然可以区分密集的点目标，但是不能有效地抑制噪声，并且会产生一定的旁瓣及杂波；而本文方法在区分密集点目标的同时有效地抑制了原图像中的噪声。对比图5～图8可以看出，本文提出的超分辨率方法同时达到了提高舰船目标SAR图像的分辨率及抑制杂波和噪声的效果。

为了验证本文算法的有效性，利用本文方法对实测数据进行处理。实测数据来源于某雷达对海面进行的扫描探测，雷达系统的部分参数为：中心频率1×109Hz，带宽3×107Hz，脉冲持续时间5×10-6s。原始图像和利用本文方法处理后的结果如图9所示，坐标单位为m。通过对比可以看出，利用本文提出的方法对实测数据进行处理后，图像的分辨率得到了一定的提高。

图9 利用本文方法处理实测数据的结果Fig.9 The result of raw data by the proposed algorithm

以上仿真和实测数据计算结果表明，本文方法能有效提高SAR图像分辨率。

4 结束语

本文通过研究现有SAR图像超分辨率方法之间的联系，针对舰船目标的模型特点，提出一种基于Fourier字典的稀疏表示方法与正则化方法结合使用的SAR图像超分辨率方法。现有的SAR图像超分辨率方法在处理舰船目标SAR图像时存在一定的缺陷，其中稀疏表示法可以有效提高目标密集图像中点目标的分辨率，但是会产生一些旁瓣和杂波，并且对噪声的抑制能力较差；正则化方法可以有效地增强SAR图像中感兴趣的特征点，从而在一定程度上消除点目标周围的旁瓣和杂波，并可在点增强的同时有效地抑制原SAR图像中的噪声，但是它对点目标密集图像的处理结果较差。本文提出的超分辨率方法既可以有效地提高点目标密集图像的分辨率，抑制原SAR图像中的噪声，又可减少结果中的杂波和旁瓣。仿真计算结果证明，本文方法比稀疏表示法和正则化方法更适合舰船目标的SAR图像超分辨率处理。

[1] Poggio T，Torre V，Koch V.Computational Vision and Regularization Theory[J].Nature，1985，317（6035）：314～319.

[2] Candes E J，Donoho D L.New Tight Frames of Curvelets and Optimal Representations of Objects with Piecewise C2 Singularities[J].Communications on Pure and Applied Mathematics，2004，57（2）： 219 ～266.

[3] Le Pennec E，Mallat S.Sparse Geometric Image Representations with Bandelets[J].IEEE Transactions on Image Processing，2005，14（4）： 423 ～438.

[4] Selesnick IW，Baraniuk R G，Kingsbury N C.The Dual-tree Complex Wavelet Transform[J].Signal Processing Magazine，2005，22（6）： 123 ～151.

[5] Gerry M J，Potter L C，Gupta I J，et al.A Parametric Model for Synthetic Aperture Radar Measurements[J].IEEE Transactions on Antennas and Propagation，1999，47（7）： 1179 ～1188.

[6] Wang Y，Liu H.A Hierarchical Ship Detection Scheme for High-resolution SAR Images[J].IEEE Transactions on Geoscience and Remote Sensing，2012，50（10）： 4173 ～4184.

[7] Donoho D L.Compressed Sensing[J].IEEE Transactions on Information Theory，2006，52（4）： 1289 ～1306.

[8] Tropp JA.Recovery of Short，Complex Linear Combinations Via l1Minimization[J].IEEE Transactions on Information Theory，2005，（4）： 1568 ～1570.

[9] Chen J，Huo X.Sparse Representations for Multiple Measurement Vectors（MMV）in an Over-complete Dictionary[C]//International Conference on Acoustics，Speech，and Signal Processing，2005.Philadelphia： PA，March，2005：18～23.

[10] Çetin M，Karl W C.Feature-enhanced Synthetic Aperture Radar Image Formation Based on Nonquadratic Regularization[J].IEEE Transactions on Image Processing，2001，10（4）：623 ～631.