三阶软件锁相环变带宽技术研究*

闫 迪，郑海昕，陈 竹

（装备学院 北京 101416）

引 言

多测速雷达系统[1]利用多部雷达的速度测量值完成导弹飞行试验的高精度外弹道测量，其中单部雷达的测速精度是影响系统测量精度的重要因素之一，而多普勒频率提取精度的提高则是单部雷达测速精度提高的关键。自适应变带宽技术一般用于锁相环快速捕获中，文献[2]用环路输入和输出频差控制环路滤波器的参数，频差较大时采用大的带宽缩短捕获时间。文献[3]根据环路是否锁定及相位误差大小对环路带宽进行调整，当相位误差较大时，使用较大带宽。现役的测速雷达通常采用数字锁相环[4]，带宽一般分档可变，实际任务中为了提高目标跟踪的可靠性，环路带宽设置较大，且设置之后一般不再改变，若任务中需要变化带宽，则直接改变锁相环参数，即采用带宽硬切换的方法，但这会引起环路失锁重捕，损失一部分测速数据。

本文分析了带宽硬切换导致的环路震荡失锁问题，借鉴自适应变带宽技术，研究在保持环路锁定状态下，进行带宽软切换的方法。对变带宽涉及的环路锁定状态判决、最佳带宽确定等问题展开研究，并在低载噪比下作带宽软切换仿真。

1 三阶软件锁相环

1.1 锁相环原理

在连续波雷达中，通过锁相环提取回波信号的多普勒频率得到目标的径向速度。锁相环是一个闭环的相位负反馈控制系统，由鉴相器、环路滤波器和数控振荡器三个基本部件组成，相位传递模型[5]如图1

所示。Kd是鉴相增益，Hloop（s）是环路滤波器传递函数，K0/s是数控振荡器传递函数。

图1 锁相环相位传递模型Fig.1 Phase transfer model of PLL

三阶锁相环Z域传递函数是

其中，m、ζ和ωn是环路滤波器参数，K=KdK0，Ts是采样时间。

1.2 环路滤波器G2支路

假设多普勒频率如式（3）所示，a1是加速度，a2是加加速度。

三阶环相位误差传递函数是

对G2支路有

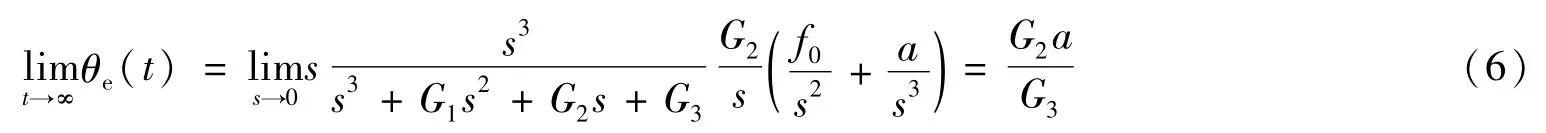
对G2支路输出进行线性拟合，即可得到a1和a2。

1.3 参数设置原则

①为了保证系统处于欠阻尼状态，即0＜ζ＜1，考虑到环路暂态时间不应太长，并具有较高的衰减速度，常取ζ=0.707。

②为了令三阶环逼近二阶环，保证m≥5，一般取m=5。

③ζ、m一旦确定后，环路带宽Bl与ωn呈线性关系，如式（7）所示。ωn是与锁相环直接相关的参数，变带宽过程中改变的直接参数是ωn，所以下面研究中的变带宽针对ωn。

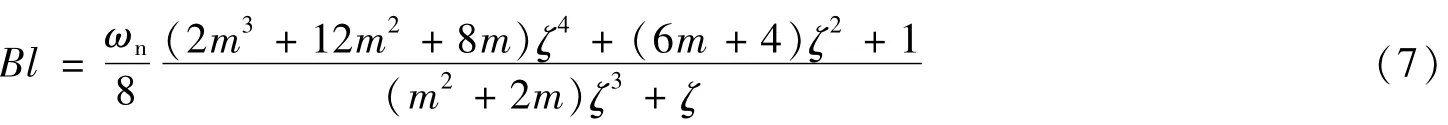
2 锁定状态判决方法

变带宽的目的是提高多普勒频率提取精度，同时保持锁相环锁定状态，这里有必要对锁相环锁定状态的判决方法进行研究，通常有以下两种判断依据。

①I、Q支路输出

假设锁相环输入信号是：

其中，fc是输入信号频率，φ1是输入信号初相。

锁定状态下，NCO输出I、Q两路信号分别是：

其中，φ2是本地NCO信号初相。

混频并滤去高频分量后，得到

②鉴相器输出

采用反正切鉴相器，由式（10）得

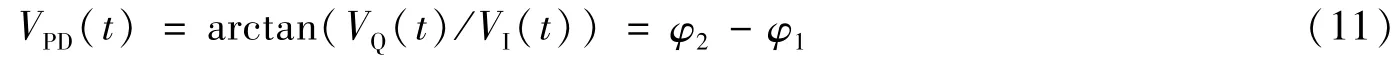
对上面两种判断方法进行仿真，如图2所示，由于鉴相器输出直接反映了本地NCO和输入信号的相位差，所以取鉴相器输出作为环路锁定判决的依据。

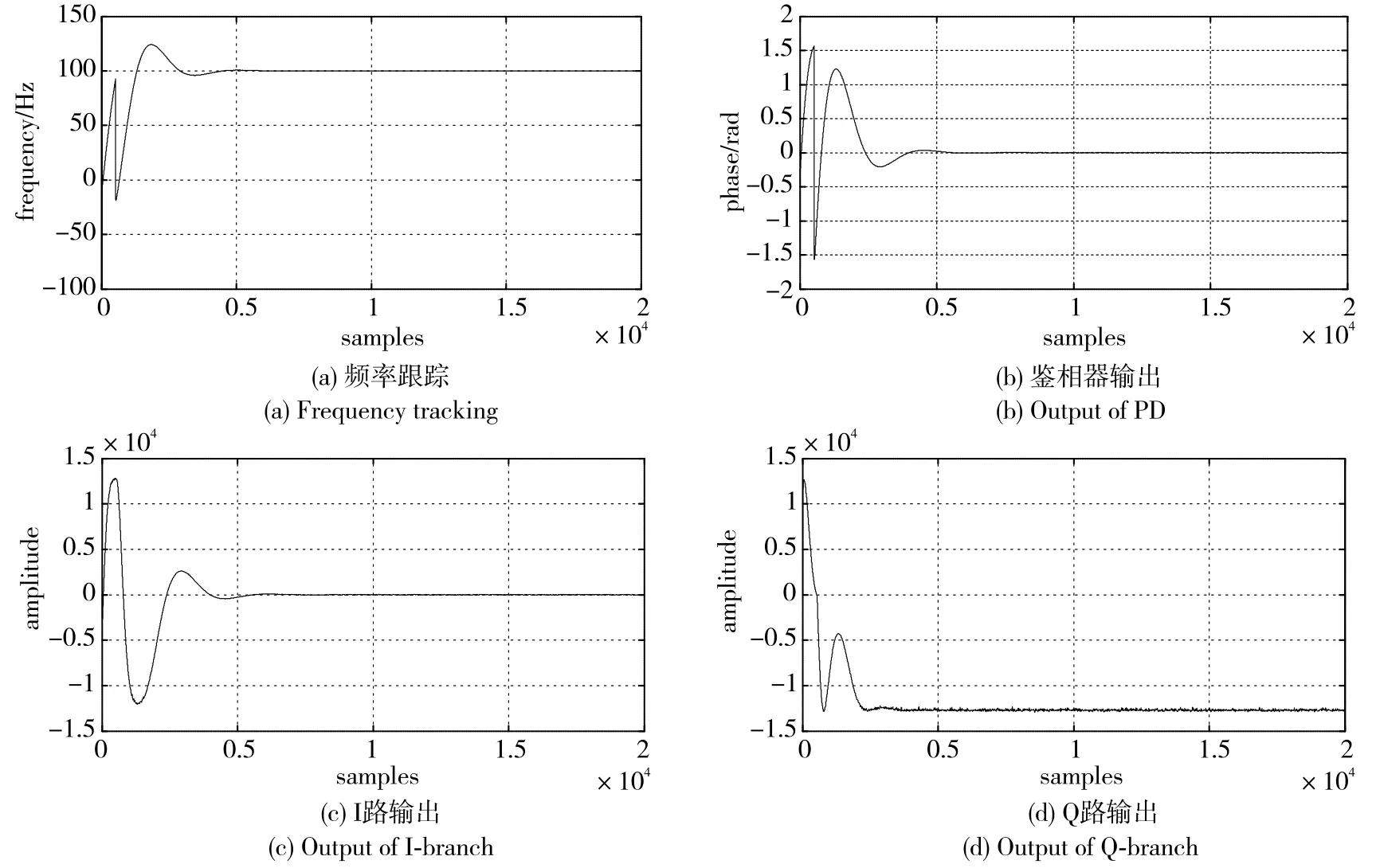
图2 频率跟踪和判决依据输出曲线Fig.2 Frequency tracking and judgement output curves

3 带宽硬切换方法

现役测速雷达带宽一般分档可变，任务中带宽需要变化时，采用带宽硬切换的方法，即直接改变锁相环参数，但会引起环路震荡失锁，导致重捕。环路带宽越小，硬切换导致的震荡失锁越明显。

仿真参数：载波中心频率fc=70MHz，采样频率fs=16.3MHz。

当多普勒频率斜升时，对ωn进行逐级硬切换，频率跟踪和鉴相器输出曲线分别如图3、图4所示。随着信号频率与NCO预置频率差别越来越大，突变之后的ωn越来越小，引起的重捕时间越来越长。

硬切换方法打破现有环路锁定状态，引起重新锁定，会损失很多有效的测速点，当信号频率与NCO预置频率之差足够大时，还要重新进行引导捕获。为了尽可能多地提取出多普勒信息，需要在变带宽过程中保持环路锁定状态。软件锁相环具有很大的灵活性，很容易对带宽变化的方式和时机进行控制，使得在保持环路锁定状态下进行变带宽成为可能。

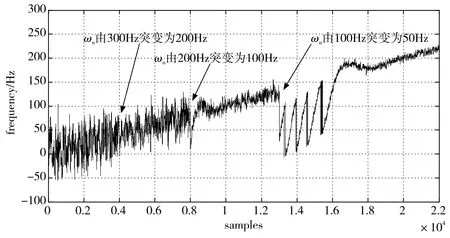
图3 多普勒频率斜升时频率跟踪曲线Fig.3 Frequency tracking curve when Doppler frequency ramps up

4 带宽软切换方法

为解决带宽硬切换造成的重捕问题，本文采用带宽软切换的方法。锁相环每处理一个数据点后，对ωn及环路参数进行更新，用新的参数处理下一个数据点。ωn在变带宽开始和停止时刻存在拐点，环路的稳定状态易受到影响。根据环路参数是否变化步长可以分为定步长和变步长法。

4.1 定步长和变步长法

带宽开始变化和停止变化时刻很容易对环路稳定性造成影响，一般开始变带宽时初始带宽较大，环路稳定状态受影响很小，但带宽停止变化时，带宽已经较小，突然停止变化会扰动环路稳定状态。

ωn线性减小即定步长变化时的频率跟踪曲线和鉴相器输出曲线如图5、图6所示。开始变带宽时，fd输出曲线和鉴相器输出曲线均十分稳定，停止变带宽时刻，鉴相器误差突然增大，fd输出也偏离了真值，这是由于ωn步长相对于ωn越来越大导致的。

图5 定步长法频率跟踪曲线Fig.5 Frequency tracking curve of fixed-step method

图6 定步长法鉴相器输出曲线Fig.6 PD output curve of fixed-step method

为了解决这个问题，本文采用变步长的方法，变化的开始阶段，步长较大，随着ωn越来越小，步长也逐渐减小。

ωn初始值是ωn_ini，变化终值是ωn_fin，变化速度是v，num是变带宽持续的时间，有

离散化后为

当ωn_ini=350Hz，ωn_fin=25Hz，num=65000时，ωn变化曲线和步进曲线如图7所示，步长越来越小。按照这种变化规律进行变带宽仿真，结果如图8、图9所示。

图7 ωn变化及步长曲线Fig.7 ωnand step-length curves

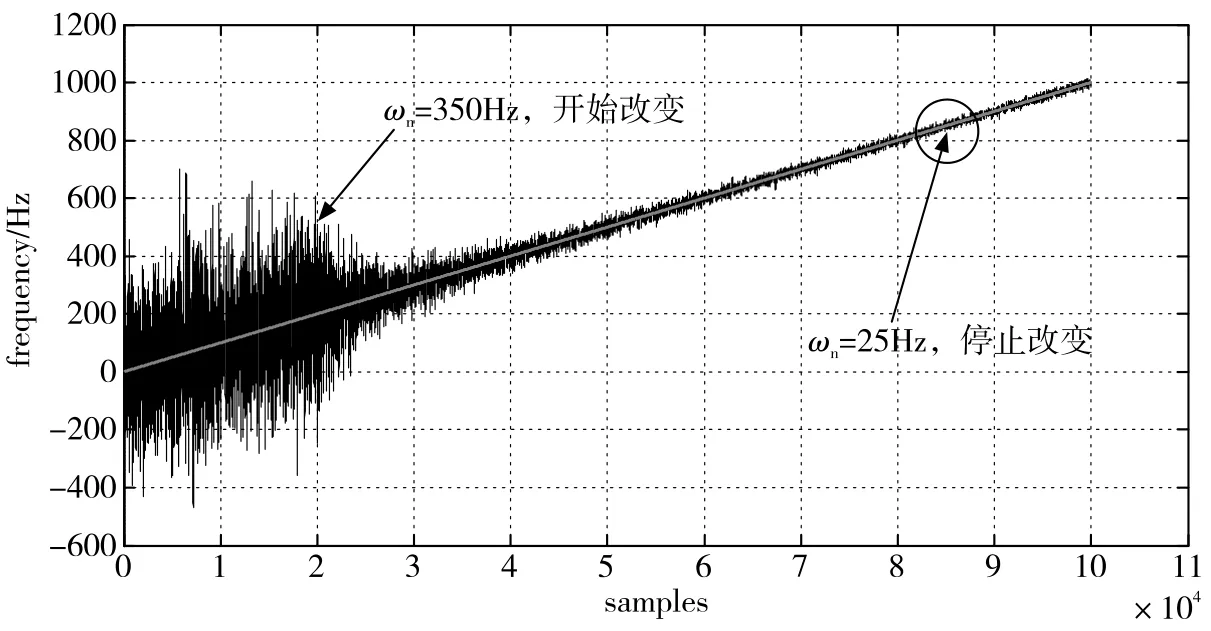
图8 变步长法频率跟踪曲线Fig.8 Frequency tracking curve of variable-step method

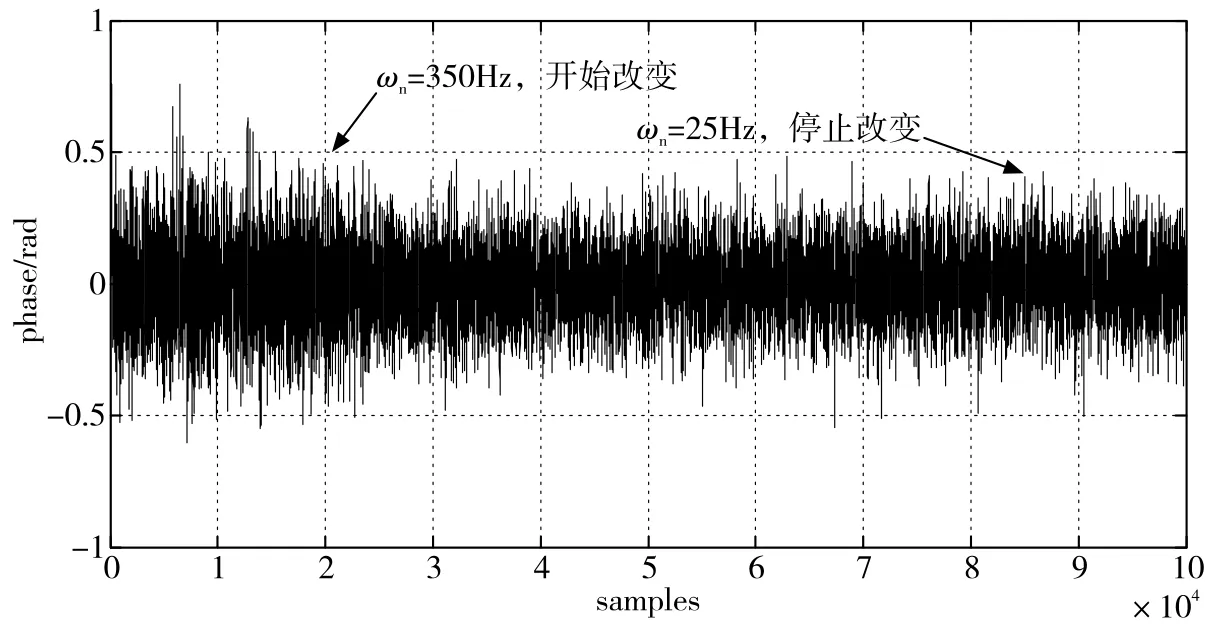
图9 变步长法鉴相器输出曲线Fig.9 PD output curve of variable-step method

对比图5、图6和图8、图9可以看出，采用变步长法后，在带宽变化停止时刻，环路仍然保持稳定状态。变步长法带宽的减小集中在前期，后期主要是ωn的平滑，防止出现大的步进引起环路波动。

4.2 ωn_fin确定准则

为提高测速精度，需尽可能将ωn_fin压窄，但是不能影响环路的正常跟踪，根据1.2节内容，可以从G2支路得到多普勒频率的加速度和加加速度信息，计算出ωn_fin的理论值。

三阶环可以无误差跟踪多普勒频率加速度，但跟踪加加速度时存在固定相位差[5]。环路若要保持跟踪状态，则固定相位差不能超过。由式（6）可得：

环路相位传递动态方程[5]是：

其中，

p

是微分算子，

是环路滤波器传输算子，

如图1所示。

对式（16）进行求解，得到：

一般情况下，mξ=5×0.707，得到：

上面的推导没有考虑到噪声的影响，相位噪声引起相位差围绕真值上下波动，致使ωn_fin比式（19）大。

4.3 变带宽仿真

为验证本文方法可行性，对多普勒频率存在加加速度的情况进行仿真，变步长法和带宽硬切换的频率跟踪曲线分别如图10、图11所示。仿真参数：ωn_ini=350Hz，ωn_fin=35Hz，num=80000，载噪比为54dBHz。

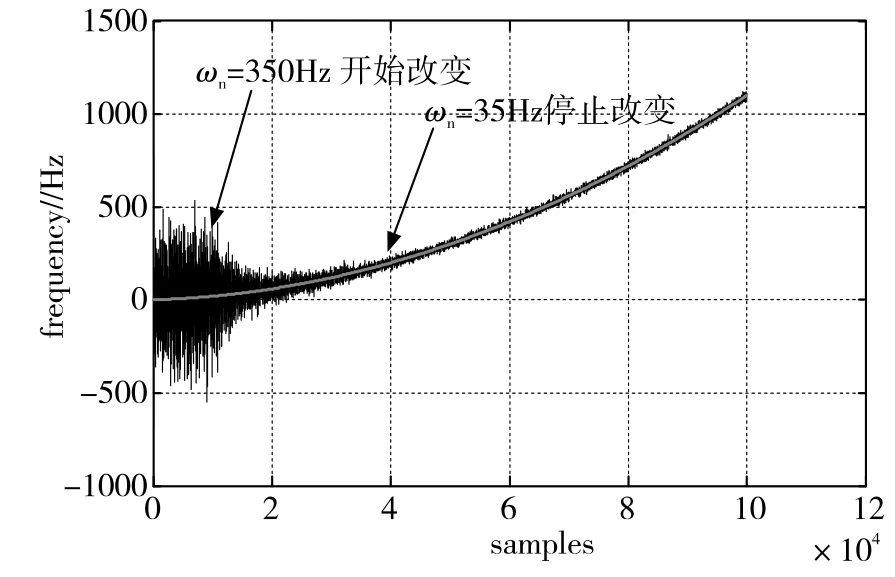
图10 多普勒频率存在加加速度情况下变步长法频率跟踪曲线Fig.10 Frequency tracking curve of variable-step method on jerk condition

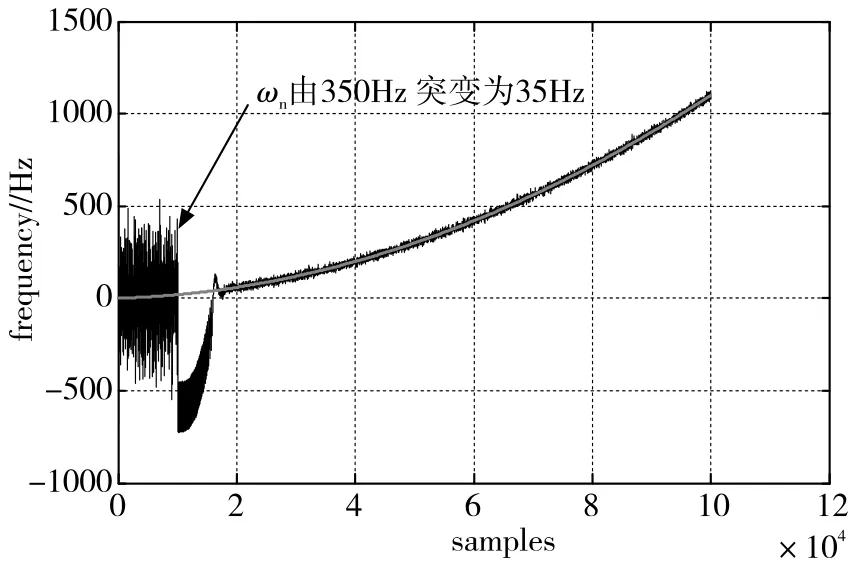
图11 多普勒频率存在加加速度情况下带宽硬切换频率跟踪曲线Fig.11 Frequency tracking curve of hard switching method on jerk condition

对比图10、图11可以看出，ωn由350Hz变化到35Hz，两种方法使用时间基本相同，但是变步长法避免了环路重捕。

5 结束语

本文对三阶软件锁相环变带宽技术进行研究，对G2支路进行线性拟合得到多普勒频率加速度和加加速度。以鉴相器输出为环路稳定的判决依据，采用带宽变步长软切换的方法，在保证环路稳定的前提下，将带宽尽可能压窄，从而获得精度更高的测速数据。该方法避免了带宽硬切换时引起的环路重捕。

[1]郭军海，吴正容.多测速雷达弹道测量体制研究[J].飞行器测控学报，2002，21（3）：5～11.Guo Haijun，Wu Zhengrong.Research on Multi-Doppler Radar Ballistic Measurement System[J].Journal of Spacecraft TT&C Technology，2002，21（3）：5～11.

[2]Dina M，Abdelhalim Zekry，Mohamed Abouelatta.Speeding-up Phased-locked Loops Based on Adaptive Loop Bandwidth[J].International Journal of Computer Applications，2013，61（3）：31～36.

[3]Joonsuk Lee and Beomsup Kim.A Low-Noise Fast-Lock Phased-Locked Loop with Adaptive Bandwidth Control[J].IEEE Journal of Solid-state Circuits，2000，35（8）：53～58.

[4]Mark A，Wickert.Phase-Locked Loops with Application[M].ECE Lecture Notes.Portland，2004.

[5]张厥盛，郑继禹，万心平.锁相技术[M].西安：西安电子科技大学出版社，2000：21～25.Zhang Juesheng，Zheng Jiyu，Wan Xinping.Phase Lock Technique[M].Xi’an：Xidian University Press，2000：21～25.

[6]郑君里，应启珩，杨为理.信号与系统[M].北京：高等教育出版社，2000：216～218.Zheng Junli，Ying Qiheng，Yang Weili.Signals and Systems[M].Beijing：Higher Education Press，2000：216～218.