双线圈电磁反力式混合型主动悬架研究

徐曹宗，陈昆山，居晨阳

XU Cao-zong, CHEN Kun-shan, JU Chen-yang

（江苏大学 汽车与交通工程学院，镇江 212013）

0 引言

悬架是汽车的重要组成部分。传统的被动悬架很难折中汽车的操纵稳定性和平顺性，而主动悬架能很好地调和它们之间的矛盾，使汽车性能大大提高。但由于主动悬架的功耗较大，其应用范围受到了限制。文献[1]讨论了一种在被动悬架基础上加装电磁反力式作动器的混合型主动悬架。该新型悬架由被动结构来承载簧载质量、衰减部分振动，其作动器产生的作动力仅作用于簧载质量或非簧载质量上，功耗较全主动悬架来说较小，且具有良好的悬架减振性能，因此有很好的使用前景。为了进一步提高该新型悬架的稳定性和减振性能，本文将自感应线圈集成在电磁反力作动器[2]中，将其安装在车轮环节上构成混合型主动悬架，通过“空钩”阻尼控制来抑制车轮振动，间接地衰减车身振动。

图1 双线圈电磁反力作动器

1 双线圈电磁反力作动器

1.1 作动器模型

在文献[2]设计的电磁反力作动器中增设次线圈，布置如图1所示。主线圈中通有激励电流Ia时，它会与永磁铁m产生相互作用力。当永磁铁受力运动时，整个作动器会对外界输出作用力ft，同时闭合次线圈中会产生感应电动势。

其中me为作动器安装对象的质量；k为作动器刚度；c为作动器阻尼力系数；x、x1分别为永磁铁和安装对象的垂向位移；fa为作动器内部的电磁力；Zs为次线圈的输出阻抗，设计取较大值，为了减小次线圈的电磁阻尼力；Us为次线圈的输出电压。作动器参数如表1所示（ψp为主线圈电磁力常数）。

作动器内部永磁铁的运动学方程为：

将上述方程进行一次拉氏变换（设x、x1初值为零）得：

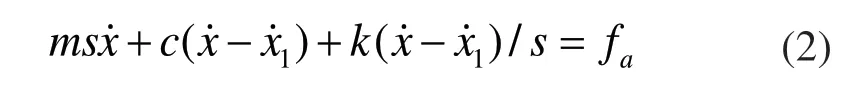
次线圈中的感应电动势主要包括互感电动势、自感电动势和动生电动势[3]，即Zs的端电压Us可以表示为：

表1 作动器参数

其中Ls为次线圈自感系数；ψs为次线圈电磁力常数；M为主次线圈的互感系数；Is为闭合次线圈中的感应电流。

电磁力fa（主动控制力）是主线圈激励电流Ia和闭合次线圈感应电流Is在磁场中共同作用产生的：

1.2 主动控制特性

研究该作动器的主动控制特性时，设安装对象保持固定不动[4]。根据式（2）～式（4），可以得到Us关于Ia的传递函数G(s)。同时设反馈传递函数为H(s)，参考输入为Ic，相应的控制系统如图1所示。

传递函数G(s)为：

其中： skcmsA /++= 。

另外，控制电流Ia满足关系式：

次线圈输出电压Us随主线圈输入电流Ia的主动控制特性如图2所示。由于主次线圈之间存在互感作用，作动器主动控制特性曲线在其共振频率之后的高频区域会产生一反共振峰，随着M的增大，反共振峰左移，此时可控频带范围减小。根据公式M=(LsLp)1/2（Lp为主线圈电感系数），为了减小M值，在Lp确定的情况下，应尽量减小次线圈自感系数Ls，即减小次线圈绕组的体积及单位匝数。但要保证次线圈电压在可控频带内能很好地反映动生电动势[5]，即反映永磁铁与安装对象的相对速度，此时的ψs不能太小。次线圈设计参数如表1所示。

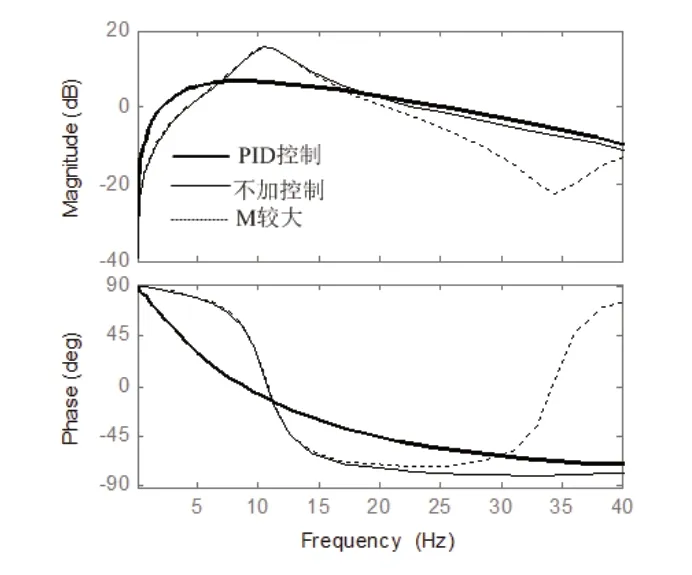
图2 主动控制特性(Kp=0.3,Ki =-20,Kd =-0.003）

传递函数H(s)选用经典的PID控制。通过调整参数Kp、Ki、Kd，能够减小作动器固有频率，并且在其共振频率处受到很好的阻尼作用，这样做能够提高下文所述悬架系统的稳定性。加PID控制后，作动器的闭环传递函数用图2中的粗线表示。此时作动器的固有频率由10.7Hz降低到8.5Hz附近，且共振峰被削减。在较宽的频带内幅频特性稳定，同时相位变化平缓，这有利于主动控制。

2 混合型主动悬架

2.1 悬架模型

本文研究的混合型主动悬架是在普通被动悬架的车轮环节上加装一个双线圈电磁反力作动器。经简化后的三自由度振动系统1/4车辆模型如图3所示。当主线圈不通电且次线圈开路时，作动器即为普通的动力吸振器。

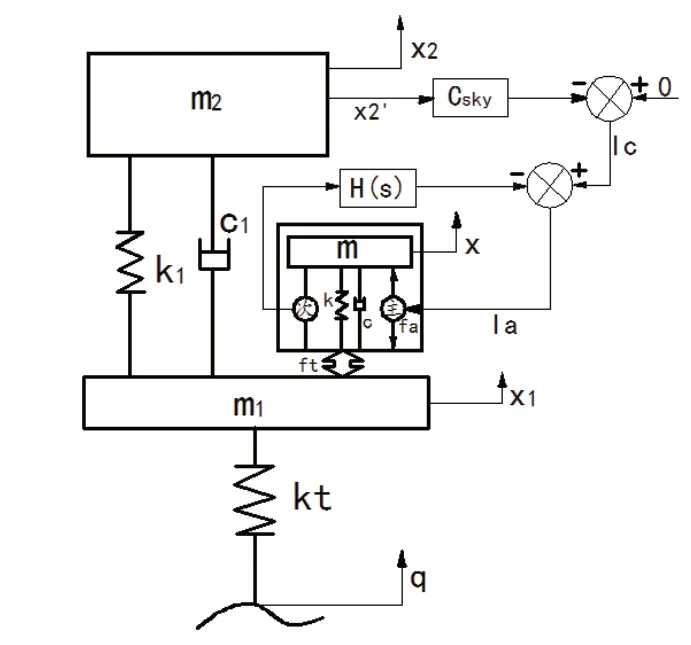
图3 混合型主动悬架模型

其中m1为车轮质量；m2为车身质量；k1为被动悬架刚度；c1为被动悬架阻尼力系数；kt为轮胎刚度；q、x1、x2、x分别为路面激励、轮胎、车身和永磁铁的位移。具体参数如表2所示。

混合型主动悬架系统的运动微分方程可以表示为：

表2 混合型主动悬架参数

2.2 双反馈控制

电磁反力作动器通电时对安装对象的作用力ft表示为：

结合式（2）～式（4）、式（6），ft可以表示为Ic和x1´的表达式：

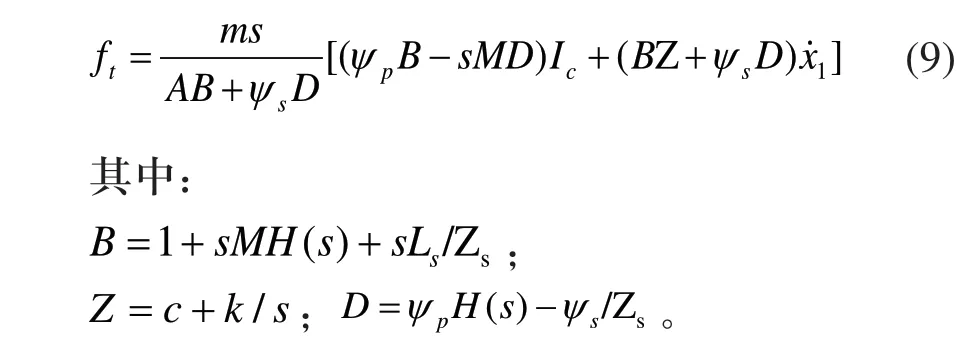
式(9)可以简化为：

其中：

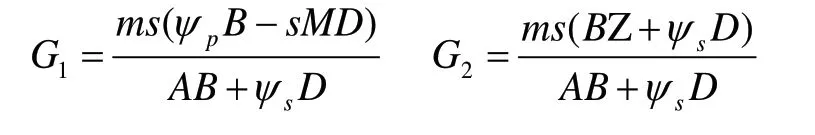
把式(10)代入式(7)得：

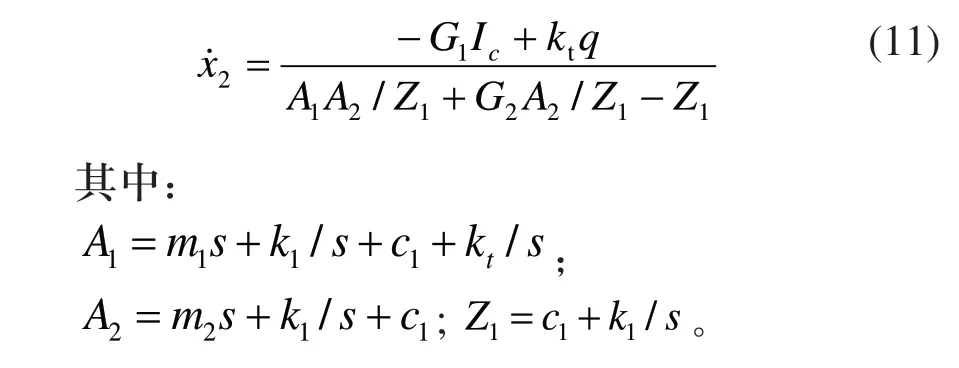
如图3所示的混合型主动悬架控制系统，内环采用了上文提到的次线圈电压反馈PID控制，而外环通常采用“空钩”、“地钩”或两者结合的阻尼控制，这里选用“空钩” 阻尼控制，取车身垂向运动速度作为反馈量，可以得到表达式：Ic=-Csky·x2´（其中Csky为“空钩” 阻尼系数）。

由式(11)知，混合型主动悬架系统的开环传递函数为式(12)，相应的Nyquist曲线如图4所示。可以发现，在相同的外环增益Csky=-180条件下，增设内环控制可以增加控制系统的稳定性裕量，使原本不稳定的系统变稳定。换言之，较单反馈控制Ia=-Csky·x2´来说，双反馈控制可以获得更大的外环增益来更好地抑制车轮振动。

结合式（7），可以获得混合型主动悬架的车身加速度，悬架动挠度和轮胎动载荷的传递函数。用MATLAB求其频率特性，如图5、图6所示。由图5可以看出，单反馈控制时电磁反力作动器具有很明显的动力吸振特性。此时车身加速度和悬架动挠度的幅频特性仅在8Hz～15Hz范围内得到改善，而新增的两个波峰使幅频特性有所恶化。当增设内环控制后，车身加速度和悬架动挠度的幅频特性在5Hz～20Hz内得到改善，频带宽度提高了2倍多，而且在周围的频域并没有出现幅频特性恶化的情况。值得注意的是，双线圈结构加双反馈控制使车身加速度和悬架动挠度的幅频特性在较宽的频带内实现了理想的天棚阻尼。由图6可以看出，轮胎动载荷的幅频特性在1.5Hz～8Hz内较被动悬架有明显增大，但从相频曲线可以发现，此频带内曲线接近180°，即路面速度输入与相对动载荷方向相反，也就是说，路面速度输入向上时，相对动载方向向下，接地性反而改善了，可以认为轮胎动载荷的幅频特性在1.5Hz～22Hz的宽范围内得到改善。

图4 混合型主动悬架系统开环传递函数

图5 车身加速度和悬架动挠度幅频特性

3 结束语

1）双线圈电磁反力作动器通过次线圈电压反馈控制后，作动器的主动控制特性得到优化，这有利于主动控制。

图6 轮胎动载荷频率特性

2）双线圈结构加双反馈控制应用于混合型主动悬架后，不仅增加了该新型悬架系统的稳定性裕量，还提高了其减振性能，在较宽的频带内改善了汽车综合性能。

[1] 陈昆山,胡思明,戴建军.基于作动力反馈控制的电磁反力式混合型主动悬架[J].噪声与振动控制,2008,28(4):70-74.

[2] 戴建军.电磁反力式混合型主动悬架作动器研究与设计[D].镇江:江苏大学,2008.

[3] 程守洙,江永之.普通物理学[M].北京:高等教育出版社,2006.

[4] L. Benassi, S.J. Elliott, P. Gardonio. Active vibration isolation using an inertial actuator with local force feedback control[J].Journal of Sound and Vibration,2004, 276:157-179.

[5] C. Paulitsch,P.Gardonio, S.J. Elliott, et al. Design of a lightweight electrodynamic, inertial actuator with integrated velocity sensor for active vibration control of a thin lightly-damped panel[C].Belgium: ISMA Publications, 2004:239-254.

[6] S.J. Elliott, M. Serrand, P. Gardonio. Feedback stability limits for active isolation systems with reactive and inertial actuators[J].Journal of Vibration and Acoustics, 2001, 123:250-261.

[7] 薛定宇,陈阳泉.基于MATLAB/Simulink的系统仿真技术与应用[M].北京:清华大学出版社,2011.

[8] 刘军,何铁平,罗石,等.新型高效电磁反力作动器的设计[J].工程设计学报,2006,13(5),317-320.