基于滑模微分器的吸气式高超声速飞行器鲁棒反演控制①

卜祥伟，吴晓燕，白瑞阳，马 震

(空军工程大学 防空反导学院，西安 710051)



基于滑模微分器的吸气式高超声速飞行器鲁棒反演控制①

卜祥伟，吴晓燕，白瑞阳，马 震

(空军工程大学 防空反导学院，西安 710051)

针对吸气式高超声速飞行器气动推进结构弹性耦合运动学模型，提出了一种基于滑模微分器的鲁棒反演控制器设计方法。分别采用反演和动态逆方法设计虚拟控制量和实际控制量。引入滑模微分器来精确估计虚拟控制量的导数，避免了传统反演控制方法“微分项膨胀”问题。基于滑模微分器，设计了一种非线性干扰观测器，可对模型不确定项进行精确估计和补偿，从而增强了控制器的鲁棒性。仿真结果表明，该控制器对模型不确定性和气动弹性影响具有较强的鲁棒性，且能实现对速度指令和高度指令很好的跟踪效果。

吸气式高超声速飞行器；鲁棒反演控制；滑模微分器；非线性干扰观测器

0 引言

吸气式高超声速飞行器作为一种未来战略打击和运载工具，有着诸多传统飞行器所不具备的优越性。特殊的机体/发动机一体化设计，乘波体气动外形布局和柔性复合材料的大量使用导致其在动力学特性和控制方式上较传统飞行器又有较大差异。具体表现在动力学模型的高不确定性、快时变性、强非线性和强耦合性，且飞行过程中伴随显著的弹性效应[1-3]。机体弹性振动轻则影响机载仪器工作精度和乘客乘坐品质，重则降低机体疲劳强度甚至导致飞行器解体。同时，弹性振动也给控制器的设计带来了新的挑战。

已有研究多是基于Winged-Cone刚体模型进行的[4-6]，这在一定程度上降低了控制器设计难度，但其控制策略的工程可靠性却难保证。因此，开展基于弹性体模型的控制器设计研究显得尤为重要。针对吸气式高超声速飞行器强耦合高阶非线性弹性体模型，传统鲁棒控制过于保守，单纯动态逆控制鲁棒性又差，滑模控制因为控制输出常常伴有高频抖振，于飞行器弹性振动抑制十分不利，且无法处理模型的非匹配不确定问题。基于以上问题，反演控制以其易于处理模型非匹配不确定问题，在近年来获得较快发展，且在飞行器控制中已有较多应用。文献[7]考虑控制输入受限问题，基于反演和动态逆设计控制器，采用自适应策略来增强控制器的鲁棒性，但该研究没有考虑弹性状态影响。文献[8]采用反演策略设计控制器，针对仅部分状态可测的情况，采用滑模微分器对不可测状态进行重构，解决了部分状态不可测时的控制问题。文献[9]研究了存在参数不确定和扰动时的弹性体高超声速飞行器自适应控制问题，基于反演和动态面设计控制器，通过设计一种模糊-神经网络干扰观测器，解决了单纯反演控制鲁棒性不强的问题。但文献[8-9]采用的是简化后的弹性体模型，没有考虑弹性状态对刚体状态的影响。针对吸气式高超声速飞行器气动推进结构弹性耦合模型，文献[10]采用反演方法设计控制器，通过引入干扰观测器来增强控制器的鲁棒性，但当加入有界扰动时，高度跟踪精度较差且控制量超限。文献[11-13]通过在控制权限中增加鸭翼偏转角，分别采用动态逆和反演方法设计控制器，很好地抑制了机体弹性振动。但对于高超声速飞行器这一类高阶系统，传统反演控制存在虚拟控制量求导复杂问题，常规解决方法是采用动态面技术，通过引入一阶低通滤波器来近似估计虚拟控制量的导数[9]。但是，动态面技术精度有限，处理不好会导致控制输出抖振[14]。

本文将研究吸气式高超声速飞行器气动推进结构弹性耦合模型的鲁棒反演控制问题。分别采用反演和动态逆方法设计控制器，引入滑模微分器精确估计虚拟控制量的导数，设计了一种基于滑模微分器的非线性干扰观测器，显著增强了控制器的鲁棒性。最后，通过实例仿真对所设计控制器的有效性进行验证。

1 高超声速飞行器模型及面向控制建模

吸气式高超声速飞行器纵向运动学方程为

(1)

为了便于控制器的设计，将模型(1)中的T、D、L和M以及Ni(i=1,2,3)拟合成如下形式

吸气式高超声速飞行器控制系统的主要任务是通过调节控制量Φ和δe，在纵向平面内实现速度V和高度h对参考输入Vref(t)和href(t)的稳定跟踪，在保证刚体状态稳定的同时，有效抑制机体弹性振动。

弹性振动会导致攻角和升降舵偏角摄动[10]，假设由攻角和升降舵偏角摄动而引起的T、D、L和M摄动量分别为

ΔT=T(Δα，Δδe),ΔD=D(Δα,Δδe)

ΔL=L(Δα，Δδe),ΔM=M(Δα,Δδe)

式中Δα、Δδe分别为弹性振动引起的攻角和升降舵偏角摄动量。

同时，考虑到推力、阻力、升力和俯仰力矩参数拟合存在误差，分别取为εi(i=T,D,L,M)。则模型(1)中V、γ、α和Q子系统因参数拟合和气动弹性影响而引入的误差为

(2)

(3)

则可将模型(1)转化为面向反演控制的严格反馈形式：

(4)

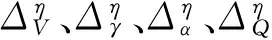
2 控制器设计

2.1 速度控制器设计

(5)

将实际控制量Φ设计为

(6)

2.2 高度控制器设计

分别定义高度、弹道角、攻角和俯仰角速度跟踪误差

(7)

沿式(7)求时间的一阶导数，则式(4)中的h、γ、α和Q子系统可化为如下形式：

(8)

将虚拟控制量和实际控制量分别设计为

(9)

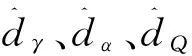
(10a)

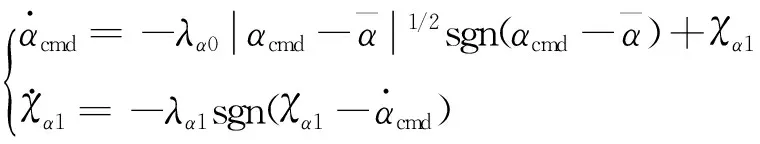
(10b)

(11)

2.3 非线性干扰观测器设计

为了对模型不确定项进行精确估计和补偿，以提高控制器鲁棒性，基于一阶滑模微分器，分别设计如下非线性干扰观测器[16]：

(12a)

(12b)

(12c)

(12d)

2.4 稳定性分析

定义微分器估计误差：

(13)

定义不确定项估计误差：

(14)

选取Lyapunov函数：

W=WV+Wh+Wγ+Wα+WQ

(15)

其中

沿Wi(i=V,h,γ,α,Q)求时间的一阶导数，并根据式(5)～式(14)得

(16)

对于式(16)，有

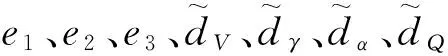
(17)

3 实例仿真

为了验证控制策略的有效性，对模型(1)进行闭环系统仿真，模型气动参数和飞行器几何参数见文献[11]。取ζi=0.02(i=1,2,3)，ω1=20.2 rad/s，ω2=48.4 rad/s，ω3=95.6 rad/s。取初始速度V=2 331.7 m/s，初始高度h=26 212.8 m。保持飞行动压q=90 148 Pa不变，速度阶跃ΔV=351.6 m/s，高度阶跃Δh=1 828.8 m。高度参考输入由阻尼为0.95、自然频率为0.03 rad/s的二阶参考模型给出。

仿真采用定步长的四阶Runge-Kuta法数值求解，步长选为0.01 s。为了验证控制器的鲁棒性，向系统(1)加入干扰，取扰动ΔV=0.61sin(0.01πt) m/s，ΔQ=1.79sin(0.01πt) °/s；同时，考虑到速度V为较大量，因此扰动Δγ,Δα为小量，取Δγ=Δα=0 °。控制器参数取为kV,1=20,kV,2=1，kh,1=1.5，kh,2=0.5，kγ,1=1.5，kγ,2=0.3，kα,1=2，kα,2=1，kQ,1=1.5，kQ,2=0.5。滑模微分器的设计参数分别取为λγ0=λα0=0.094 9，λγ1=λα1=0.001 5，λQ0=3，λQ0=1.5，λQ1=1.1。非线性干扰观测器参数取为ΓV0=0.82，ΓV1=0.33，Γγ0=Γα0=0.001 5，Γγ1=Γα1=10-6，ΓQ0=0.047 4，ΓQ1=0.001 1。

仿真结果如图1～图6所示。图1、图2和图4中的下标“1”表示未加干扰，下标“2”表示加入干扰。从仿真结果可看出，控制器对模型不确定项具有较强的鲁棒性，速度跟踪和高度跟踪精度高，且跟踪误差收敛快；弹道角、攻角和俯仰角速度都能维持在合理的范围内，且最终都能达到稳态；前三阶弹性状态抑制较好，能够较快达到稳定状态；控制量Φ和δe较平滑，无高频抖振，且始终都能维持在合理的范围内。

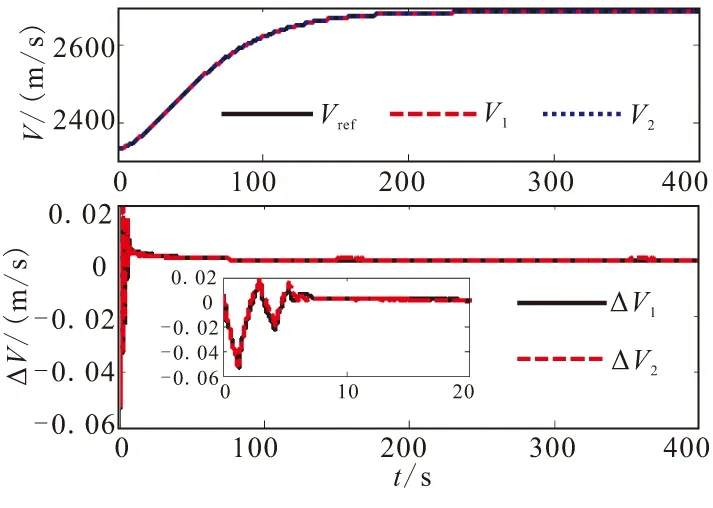
图1 速度跟踪曲线和跟踪误差Fig.1 Velocity command tracking curve and tracking error

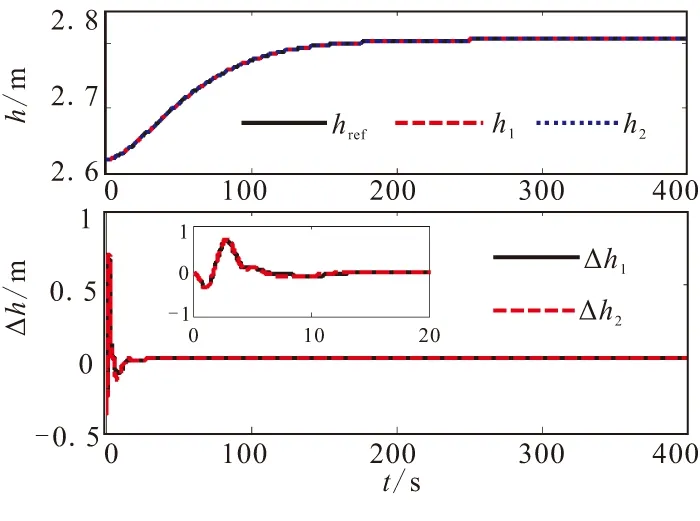
图2 高度跟踪曲线和跟踪误差Fig.2 Altitude command tracking curve and tracking error

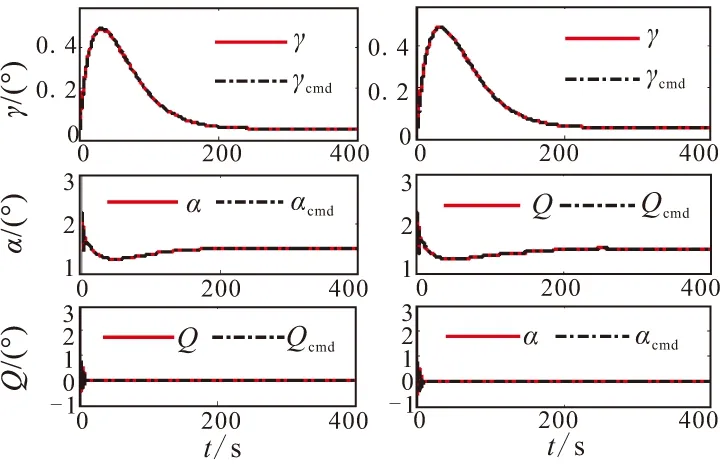
(a)未加干扰 (b)加干扰

图4 控制输入Fig.4 Control inputs

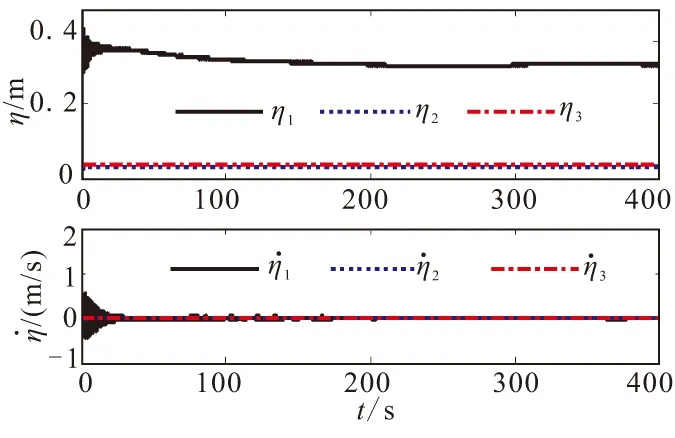
图5 弹性状态响应及变化率曲线Fig.5 Elastic states response and change rate curves

(a)不加扰动时收敛过程

(d)dV和dQ估计曲线

4 结论

(1)针对吸气式高超声速飞行器弹性体模型，设计了一种鲁棒反演控制器。在控制器设计过程中，引入滑模微分器来获取虚拟控制量的导数，避免了传统反演设计中“微分膨胀”问题。基于滑模微分器，设计了一种非线性干扰观测器，可实现对模型不确定项的有效估计。

(2)仿真结果表明，所设计控制器对飞行器模型不确定性和气动弹性影响等不确定项具有较强的鲁棒性，能够实现较好的速度和高度跟踪效果。

[1] Hank J M,Murphy J S,Mutzman R C.The X-51A scramjet engine flight demonstration program[C]//Proceedings of 15th AIAA International Space Planes and Hypersonic System and Technologies Conference. Reston,VA,USA:AIAA,2008:1-13.

[2] Hu Xiaoxiang,Wu Ligang,Hu Changhua,et al.Adaptive sliding mode tracking control for a flexible air-breathing hypersonic vehicle[J].Journal of the Franklin Institute,2012,349:559-577.

[3] Luo Xiong,Li Jiang.Fuzzy dynamic characteristic based attitude control of hypersonic vehicle in gliding phase[J].Science China Information Sciences,2011,54(3):448-459.

[4] 宋超，赵国荣，陈洁.基于鲁棒滑模观测器的高超声速飞行器双环滑模控制[J].固体火箭技术，2012,35(4):438-441.

[5] 宋超，赵国荣，刘旭.高超声速飞行器的自适应容错控制[J].固体火箭技术，2012,35(5):593-596.

[6] 时建明，王洁，叶继坤，等. 吸气式高超声速飞行器输入受限自适应反演控制[J].固体火箭技术，2012,35(5):573-577.

[7] Lisa Fiorentini,Andrea Serrani.Adaptive restricted trajectory tracking for a non-minimum phase hypersonic vehicle model [J].Automatica,2012,48:1248-1261.

[8] Qun Zong,Ji Yue-hui,Zeng Fan-lin,et al.Output feedback back-stepping control for a generic hypersonic vehicle via small-gain theorem[J].Aerospace Science and Technology,2012,23:409-417.

[9] Zhou Li,Fei Shumin.Adaptive dynamic surface control for air-breathing hypersonic vehicle[J].Journal of Systems Engineering and Electronics,2013,24(3):463-479.

[10] 时建明，王洁，王琨，等. 吸气式高超声速飞行器纵向运动反演控制器设计[J].西安交通大学学报，2013,47(3):102-107.

[11] Lisa Fiorentini.Nonlinear adaptive controller design for air-breathing hypersonic vehicles [D].Columbus:The Ohio State University,2010.

[12] Lisa Fiorentini,Andrea Serrani,Michael A Bolender,et al.Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J].Journal of Guidance,Control,and Dynamics,2009,32(2):401-416.

[13] Fiorentini L,Serrani A,Michael A Bolender,et al.Nonlinear robust/adaptive controller design for an air-breathing hypersonic vehicle model[C]//AIAA Guidance,Navigation and Control Conference and Exhibit 20-23 August 2007,Hilton Head,South Carolina,USA,AIAA,2009-6283.

[14] 胡超芳，刘艳雯. 基于动态面的高超声速飞行器模糊自适应非线性控制[J].控制与决策，2013,28(12):1849-1854.

[15] Levant A.Higher order sliding mode,differentiation and output feedback control[J].International Journal of Control,2003,76(9):924-941.

[16] Yang Jun,Li Shi-hua,Sun Chang-yin,et al.Nonlinear-disturbance-observer-based robust flight control for airbreathing hypersonic vehicels[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(2):1263-1275.

(编辑：薛永利)

Sliding-mode-differentiator-based robust backstepping control of air-breathing hypersonic vehicles

BU Xiang-wei,WU Xiao-yan,BAI Rui-yang,MA Zhen

(Air and Missile Defense College,Air Force Engineering University,Xi'an 710051,China)

A sliding-mode-differentiator-based robust backstepping controller was designed for air-breathing hypersonic vehicles with aerodynamics,propulsion and structural flexible dynamics couplings.Virtual and actual control laws were designed based on backstepping and dynamic inversion design procedure respectively.Sliding mode differentiator was introduced to obtain the derivatives of virtual control laws,which avoids the explosion of differentiation terms in the traditional backstepping control.A nonlinear disturbance observer,based on sliding mode differentiator,was introduced to estimate and compensate the model uncertainties of precisely,which enhances the controller's robustness.Simulation results demonstrate the effectiveness of this controller in tracking velocity and altitude commands in the presence of model uncertainty and flexible dynamics.

air-breathing hypersonic vehicles;robust backstepping control;sliding mode differentiator;nonlinear disturbance observer

2014-02-23；

：2014-04-03。

航空科学基金(20130196004,20120196006)，陕西省自然科学基础研究计划项目(2012JM8020)。

卜祥伟(1987—)，男，博士生，研究方向为飞行器建模与控制。E-mail：buxiangwei1987@126.com

V448

A

1006-2793(2015)01-0012-06

10.7673/j.issn.1006-2793.2015.01.003