自旋导弹飞行共振稳定性研究①
2015-04-25闫晓勇
贾 宝,薛 林,闫晓勇
(1.北京电子工程总体研究所,北京 100854;2.中国航天科工集团第二研究院,北京 100854)
自旋导弹飞行共振稳定性研究①
贾 宝1,薛 林2,闫晓勇1
(1.北京电子工程总体研究所,北京 100854;2.中国航天科工集团第二研究院,北京 100854)
弹体滚转时,结构不对称等因素会对导弹的角运动产生周期性的强迫干扰。针对自旋导弹飞行过程中的周期性干扰和非线性气动特性,建立了非线性弹体角运动模型。在此基础上,采用多尺度法对自旋导弹的受迫角运动方程进行了求解,得到了近似解析解并研究了其稳定性。研究表明,当弹体转动速率接近固有频率时,气动非线性项及干扰项都将影响弹体角运动的稳定性;分析结果显示,合理地设计气动外形可避免共振不稳定的发生,这对自旋类导弹的工程研制具有一定的指导性意义。
自旋导弹;锥形运动;非线性运动;共振稳定性
0 引言
自旋导弹在飞行过程中,弹体绕其纵轴旋转,使得导弹的受力特性及运动状态复杂化。弹体滚转引起的马格努斯效应及陀螺效应导致导弹的俯仰通道和偏航通道之间出现交联。此时,弹体的角运动表现为复杂的锥形运动,即二圆运动(章动、进动)的叠加,导弹的动态稳定性将取决于锥形运动的稳定性。文献[1-3]通过建立不同的角运动方程对自旋弹的动稳定性进行了分析,分析结果均以线性化假设为基础,而导弹在实际飞行过程中受到的气动力并不是严格地与攻角成正比,在某些情况下,它们之间存在着较强的非线性关系。非线性系统的收敛特性与起始条件及输入干扰均有很大关系,Murphy最先开始了非线性因素对运动影响的研究。至今,已有一些资料给出了自旋导弹的非线性运动特性及稳定条件[4-6]。这些结果均针对导弹的自由扰动运动,得到了起始条件对导弹稳定运动的影响,而自旋导弹在飞行过程中不可避免地受到气动偏心、质量偏心、推力偏心及控制力等周期扰动的影响,这些因素也将影响非线性系统的运动稳定性[7-8],尤其是当弹体转速接近弹体固有频率时,运动特性将会变得十分复杂。现有的研究结果均建议弹体的转速设计应远离弹体的固有频率,但对于不可避免地出现重合的情况,未有系统的稳定性研究,缺乏对非线性共振有界或发散的详细认识和理论判据。
本文将利用多尺度法,研究自旋弹在气动非线性和外界干扰输入条件下的运动机理,进而得出运动过程的动稳定条件及运动特性,对于避免自旋弹出现共振不稳定飞行具有重要的设计指导意义。
1 弹体角运动方程
弹体自旋条件下,导弹的俯仰、偏航通道相互耦合,难以分开进行单独研究。为便于分析,引入复角的概念,即
δi=β*+iα*
(1)
式中α*、β*为准弹体系下的攻角和侧滑角。
[1],将运动微分方程进行降阶,得到自旋导弹的角运动方程:
(2)
其中
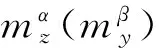
(3)
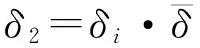
将非线性模型代入运动方程中,同时考虑由于结构不对称带来的周期扰动力矩[8],可得到自旋导弹的受迫运动微分方程:
=iA0ei(ωxt+γ0)
(4)
式中 H2=-d2a22;M2=c2a24;ωx为弹体滚转频率;A0为扰动力矩的振幅;γ0为初始相位。
2 非线性共振运动周期解
利用“系数冻结法”,式(4)可视为一个非齐次的非线性常微分方程,其自变量为复数,展成实数后方程阶次变为四阶,难以利用相平面理论进行定性分析,同时其解析解也无法得到。因此,考虑求取其近似周期解,进行近似定量分析。
2.1 多尺度法
多尺度法是由Sturrock、Frieman等人提出的一种摄动方法[10-11],其计算精度高,分析处理方便,因而得到了广泛应用。多尺度法的主要思想是引入多个时间尺度量t、εt、ε2t、…,把解看作这些独立时间尺度的函数,根据这一思想,引入新的自变量:
Tn=εntn=0,1,2,…
(5)
式中ε为小参数。
根据上面的关系式,可将解对时间t的导数变为对新变量Tn的偏导数,表示如下:
(6)
式中D0、D1、D2、…分别为对T0、T1、T2、…求偏导的运算符号。
再将微分方程的解写为
x(t)=x0(T0,T1,…)+εx1(T0,T1,…)+…
(7)
独立自变量的个数取决于展开式所取的项数。将式(6)、式(7)代入微分方程中,按照ε同次幂项系数相等的原则,建立一系列偏微分方程,由此解出x0、x1、…,从而得到微分方程的近似周期解。
2.2 共振运动的近似周期解
设系统的阻尼项、非线性项、马格努斯项及扰动项为同阶小量,则可将式(4)写为
(M2δ2+iP0T0)δi+iA0ei(ωxt+γ0)]
(8)
根据多尺度法,将解写为如下形式:
δi(t,ε)=δi0(T0,T1)+εδi1(T0,T1)
(9)
然后,代入式(8)中,可得
(10)
iP0D1δi0-(H0+H2δ2)D0δi0+
(M2δ2+iP0T0)δi0+iA0eiωxt
(11)
将式(10)的解写为如下形式:
δi0=K1ei(ω1T0+φ1)+K2ei(ω2T0+φ2)
(12)

将式(12)代入式(11)中,当滚转频率接近于弹体固有频率时,扰动项影响着解的形式,引入失调参数σ,设
ωx=ω1+εσ
(13)
则有
(14)
为得到周期解,应消除上式中的永期项,即令Q1、Q2的系数为零,然后分离实部和虚部后可得
(15)
其中
至此,便得到了求解角运动系统近似解析解的全部公式,即通过式(15)得到K1、K2、φ1、φ2,然后代入式(12),便得到角运动方程的一阶近似解。从上式可看出,非线性因素的存在使得运动振幅与频率的变化复杂化,很难直接进行求解。而对于弹体的运动稳定问题,只需要关心振幅稳态值的收敛情况即可。
(16)
从式(16)可看出,增大阻尼力矩的线性项,将抑制振幅的稳态值,这对弹体的飞行运动将是有利的。将式(16)中前2个方程平方后相加,可得
(17)
式中ξ=M2/(P0τ)。
式(17)称为频率响应方程,将其与式(16)中的第3个方程联立,即可得到关于稳态振幅的二元方程组,稳态振幅存在且稳定,就代表了角运动的稳定。

参数λ12、λ13、λ22及λ23表示了阻尼力矩的非线性项对弹体角运动的影响,如果忽略干扰因素,则这4个参数只影响弹体运动的振幅,即影响着弹体运动的稳定性;而此时静力矩非线性项M2只影响运动频率,使弹体的运动频率随时间发生变化。如果同时略去这5个参数的影响,角运动变为线性自由扰动运动,阻尼参数λ11、λ22的正负将决定弹体运动的稳定性。下面在式(15)、式(17)的基础上,建立这些参数与弹体稳定性的解析关系,为进一步开展系统动态稳定性的分析奠定研究基础。
3 非线性共振运动稳定性分析
角运动的稳定性直观的表现为振幅的收敛特性,即分析式(15)的奇点稳定性,下面根据K2的稳态值是否为零,将系统的稳态值分为2种情况,分别分析。
3.1 K2稳态值为零时的稳定性分析
K2稳态值为零时,K1最多会存在3个稳态实数解。设此时稳态解为K1=K10、η=η0,它们可通过式(17)来求得。此时,式(15)的雅克比矩阵为
(18)
矩阵A特征根的实部全部为负数是解稳定的充要条件,由此可得稳定条件为
(19)
如果忽略非线性项的影响,上面的稳定条件将变为λ11<0,λ21<0,将其展开并简化后可得
(20)
这便是线性模型下自旋导弹运动稳定的条件,与文献[1]所得结果一致。可见,在非线性影响较小时,系统的稳定性可由线性理论来得到。下面先来分析稳定条件式(19)中的前2个不等式:
(1)首先应满足式(20)的条件;其次应增加λ11、λ21的绝对值,这样不仅有利于增加稳定条件的边界,还可减小稳态振幅值K10。因此,若增强弹体动态稳定性,应增加弹体的阻尼力矩。
(2)从式(19)前2式可看出,H2为正时,对第2个条件有利而对第1个条件不利;H2为负时,对第1个条件有利而对第2个条件不利。因此,设计过程中,在满足条件(20)时,只需要考虑前2个条件中的1个即可,因为第2个条件与H2为2倍的关系,更容易造成不稳定的情况出现。所以,取H2为正值,将更有利于稳定运动。
(3)增加静稳定力矩及减小陀螺力矩P0,都将增大τ的值,这样有利于减小λ12、λ22的绝对值,从而削弱非线性项的影响,有利于弹体稳定。

当K2=0时,在式(17)的两端同时对K1进行求导,可得
(21)
如果设dωx/dK1=0,则有dσ/dK1=0,代入上式后,得到方程:
(22)
方程(22)与稳定性判别式(19)中的第三式相一致。对此方程进行求解,可得
(23)
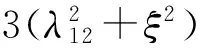
利用数值计算,将结果在ωx-K1图中表示,可对运动的稳定性进行更直观的分析。如图1所示,图中实线为根据式(17)得到的某一系统a的频率响应曲线,从中可看出,曲线发生了倾斜,最大振幅远离了ωx=ω1。图中虚线可以通过式(23)来得到,由上述分析还知,这条虚线是通过对频率响应方程求导且假设dωx/dK1=0而得到,因此它代表了不同的扰动振幅下,频率响应曲线上具有铅垂切线的点。这条虚线与频率响应曲线相交于2个点,当转速位于这2个点之间时,频率响应方程将有3个实数解:位于虚线内部的点不满足q>0,为不稳定奇点;而处于其外部的点满足。从图中及上面的分析可看出,当频率响应曲线上所有点都不具有铅垂切线时,式(19)的第三式永远满足;当存在具有铅垂切线的点时,有些转速值对应的K1具有3个稳态值,而其中有1个不满足式(19)的第三式,另2个满足。因此,式(19)的第三式只影响稳态奇点的稳定性,并不决定角运动最终的收敛特性,设计时应重点考虑式(19)的前2个不等式。
图1未表现出稳定条件(19)中的前2个条件,表明这2个条件式对系统a永远成立。事实上,这2个条件式可在图中用曲线来表示,λ12、λ22的正负,将决定满足条件的点的位置:当λ12、λ22为正时,位于曲线下方的点满足条件;当λ12、λ22为负时,位于曲线上方的点满足条件;当曲线不存在时,所有的点均满足条件。

图1 系统a的频率响应曲线Fig.1 Frequency response curves of system a

图2 系统a的相平面图Fig.2 Phase plane plot of system a
图2表示了某转速下式(15)的相平面图,此时系统存在3个不等的实数解。从中可看出,3个解中的大值R3与小值R1为稳定奇点,代表了2个稳定的周期解,而中间值R2为不稳定奇点,代表了不稳定的周期解,最终物理上实现哪一个稳态解由初始条件来决定。一个转速值对应2个稳定奇点,造成了系统在此区间内的跳跃现象,即转速连续增大或减小时,幅值并不是连续的变化,而是突然发生跳变。
图3为运动方程的数值解,上下2幅图中的弹体转速虽只相差了0.01 rad/s,但振幅变化了75%,即发生了跳跃现象。当然,如果3个奇点只有1个是稳定的,就不存在这种突变现象了。

图3 系统a攻角-时间变化曲线Fig.3 Angle of attack-time curve of system a

ω1T0+φ1=ωxT0+φ0
式中φ0为一常数。
此时,自激系统受迫运动的固有频率被激励频率所同化,固有频率在稳态运动中不再有所体现,这种现象被称为同化现象。
3.2 K2稳态值不为零时的稳定性分析
(24)
当矩阵B的特征根的实部全部为负数时,即
Re(s1,2,3)<0
(25)
稳态值将是稳定的,此时系统运动表现为二圆运动的叠加,频率分别为ωx和ω2。此矩阵十分复杂,很难得到其特征值的解析解,下面利用数值解对该平衡态的运动特性进行定性分析。
图4为某一系统b在第一种稳态值下的频率响应曲线,图中位于点划线上方的点为不稳定的,但此时并不代表角运动将会发散,非线性系统的多个稳态值保证了系统的稳定性与稳态值的稳定性是不等价的。图5为矩阵B特征值的实部,从中可看出,当系统的第一种稳态解为不稳定解时,第二种稳态解将为稳定的,即导弹随着转速的不同,将稳定于第一种稳态解或第二种稳态解。图6为利用数值解法得到的结果,当转速低于临界转速时,运动稳定于第一种稳态解,K2值为零,最终攻角(侧滑角)以转速为角频率做简谐振动;当转速高于临界转速时,运动稳定于第二种稳态解,K2值不为零,最终运动表现为二圆运动。

图4 系统b的频率响应曲线Fig.4 Frequency response curves of system b
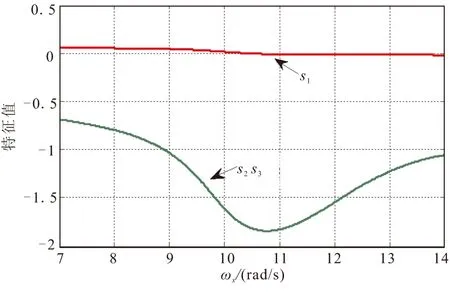
图5 系统b的矩阵B特征值Fig.5 Eigenvalue of matrix B of system b
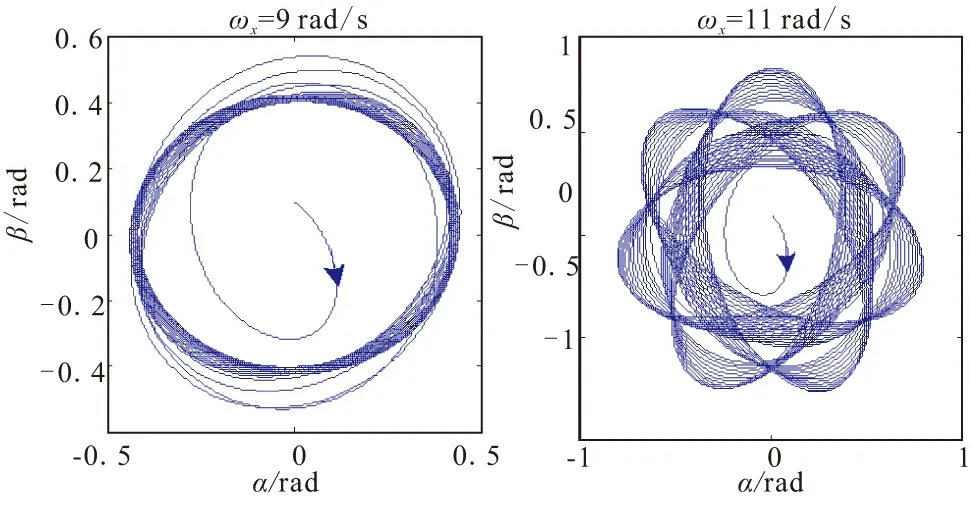
图6 系统b攻角-侧滑角变化曲线Fig.6 Pitch-yaw curves of system b
自旋导弹的非线性共振运动不仅存在多个稳态解,而且当这些稳态解均不稳定时,有可能出现运动发散现象,这是线性系统所不存在的,线性系统受迫运动的稳定性只与自由运动的稳定性有关。
4 算例仿真
以某型自旋导弹为例进行仿真分析,某特征点系统的仿真参数如表1所示。

表1 仿真参数Table 1 Simulation parameters
如果使用线性理论进行分析,式(20)即为运动稳定的判别式。计算可知,此系统满足线性稳定条件,运动最终做稳定的圆锥运动,如图7所示。
考虑非线性项的影响,设此时有H2=-2、M2=20,然后分别针对2种稳态值进行计算。K2稳态值为零时,系统存在1个奇点,即为K1=0.842,代入稳定条件式(19)后,有p=-0.676<0,即第一种稳态值不稳定;K2稳态值不为零时,系统仍只存在1个奇点,即K1=0.257,K2=0.950代入式(24)后,得到矩阵的3个特征值的实部分别为s1,2=-0.930,s3=0.197,第3个特征值的实部为正,表明第2种稳态值也不稳定。因此,该系统在非线性理论下为不稳定的,其运动将逐渐发散,如图8所示。
为使系统在非线性理论下是稳定的,可采用前文分析的利于稳定飞行的方法。例如,增加弹体的阻尼力矩,将阻尼力矩系数a22调整为-2;此时,在K2稳态值为零时,奇点值为K1=0.316,代入稳定条件式(19)后可知,此稳态值为稳定的。角运动最终稳定于一个周期运动,如图9所示。从中可看出,攻角(侧滑角)运动振幅为0.324,与理论计算结果相比误差为2.5%,误差的出现主要是因为本文采用的方法为近似算法,得到的解为近似解析解。
综上所述,在气动参数的非线性项较大而不可忽略时,根据线性稳定性理论得到的设计结果在转速接近共振频率时,并不能真实地反映动稳定性情况,需要满足文中所给出的条件式(19)或式(25)。

图7 线性理论下系统的稳定运动Fig.7 Stable motion based on the linear theory

图8 非线性理论下系统的不稳定运动Fig.8 Unstable motion based on the nonlinear theory

图9 增大阻尼后系统的稳定运动Fig.9 Stable motion with large damping
5 结论
(1)当弹体的滚转频率接近固有频率时,角运动将会出现共振现象。如果气动非线性项可忽略,则采用线性稳定理论进行分析;此时,自由运动的稳定性与受迫运动的稳定性是等价的,即扰动项不影响弹体的动态稳定性。而当气动非线性项不可忽略时,周期扰动将影响角运动的稳态运动及稳定条件,不仅使系统存在多个稳态值,而且出现了频率偏斜、振幅突变、频率同化等现象,还有可能导致系统运动的发散。
(2)在导弹的设计过程中,应极力避免导弹的设计转速接近固有频率。如果导弹飞行过程中的转速降低、闭环系统带宽变大或其他不确定因素,导致无法避免转速与固有频率相接近,则应通过增加阻尼力矩、减小陀螺效应及马格努斯效应、保证阻尼力矩非线性项为正等手段,以满足本文给出的稳定性判据,保证弹体运动的稳定。
(3)要注意自旋导弹运动过程中可能出现的“转速闭锁”现象,此时弹体转速长时间维持在一个较低的值,如果此转速接近固有频率,可能造成导弹长时间的共振运动,影响导弹的飞行性能,甚至造成运动发散。
参考文献:
[1] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京理工大学出版社,2008:248-263.
[2] Mao Xue-rui,Yang Shu-xing,Xu Yong.Coning motion stability of wrap around fin rockets[J].Science in China Series E:Technological Sciences,2007:343-350.
[3] 闫晓勇,杨树兴,张成.基于章动运动理论的火箭弹锥形运动稳定性分析[J].兵工学报,2009,30(10):1291-1296.
[4] Murphy C H.Free flight motion of symmetric missiles [R]. AD-442757,1957.
[5] Murphy C H.On the quasi-linear substitution method for missile motion caused by strongly nonlinear static moment[R].AD-410213,1963.
[6] 董亮.火箭运动的非线性动稳定判据[J].兵工学报,1984,11(4):16-26.
[7] Nayfeh H,Saric W S.Nonlinear Resonances in the motion of rolling reentry bodies[R].AIAA 71-47.
[8] Morote J.Resonant lock-in of unguided rockets having nonlinear aerodynamic properties[R].AIAA 2006-830.
[9] 洪金森,洪诗权.再入飞行器极限环运动分析[J].空气动力学学报,2005,23(2):204-209.
[10] 刘延柱,陈立群.非线性振动[M].北京:高等教育出版社,2001:83-94.
[11] Hayfeh A H,Mook D T.Nonlinear oscillations[M].New York,1979.
(编辑:吕耀辉)
Analysis of resonance stability for spinning missile
JIA Bao1,XUE Lin2,YAN Xiao-yong1
(1.Beijing Institute of Electronic System Engineering,Beijing 100854,China;2.The Second Academy of China Aerospace Science and Industry Corp.,Beijing 100854,China)
The configurational asymmetry can produce a periodic forced interference to the angular motion of missile when it rotates.On the premise of considering the periodic interference and the nonlinear aerodynamic characteristics of spinning missile,a nonlinear mathematic model of coning motion was established.By the method of multiple scales,an approximate analytic solution of nonlinear differential equation was obtained.On this basis,conditions for steady-state forced motion and their stability of spinning missile were researched.The result indicates that both of the nonlinear aerodynamic coefficients and the periodic interference affect the coning motion stability.The resonance instability can be avoided by appropriate selection of aerodynamic configuration.The research results provide theoretical support to design of the spinning missiles.
spinning missile;coning motion;nonlinear motion;resonance stability
2014-07-07;
:2014-08-25。
贾宝(1988—),男,博士生,研究方向为飞行器总体设计。E-mail:abao19881211@163.com
TJ760.1
A
1006-2793(2015)01-0023-07
10.7673/j.issn.1006-2793.2015.01.005
