基于Midas Civil 的梁式桥抗震计算研究

■黄孝杰

（福州市规划设计研究院，福州 350003）

1 前言

随着我国城市化进程加快，城市基础建设越来越迅速，道路桥梁建筑规模不断扩大，桥梁结构在不同水准地震作用下的抗震设防要求不断提高。我国公路工程旧有抗震设计采用的规范制定于1989 年，为单一水准设防、基于强度的一阶段设计，存在一定的局限性。而现行的桥梁抗震规范均为两水平设防、两阶段设计，即E1 地震作用下，结构在弹性工作范围，有足够的强度，基本不发生损伤；E2 地震作用下，结构要有足够的延性能力，可发生损伤，产生弹塑性变形，耗散地震能量，但结构的塑性铰区域应具有足够的塑性转动能力，能保护构件基本不发生损伤。因此这就要求工程师深入理解桥梁抗震设计规范与细则，然而，现行桥梁抗震设计规范对抗震计算阐述比较笼统，给设计计算分析带来一些困惑。本文结合现有抗震设计规范要求及工程实例，分别采用反应谱法与时程分析法，对梁式桥梁的抗震设计计算进行研究分析，期望能为梁式桥梁的抗震设计提供参考。

简支梁桥结构比较简单,以往地震震害中梁体本身发生破坏的情况很少,即使有梁体发生破坏,大多也是由于支座破坏或落梁等原因而引发的。受篇幅所限，本文主要针对下部结构的桥墩进行抗震设计计算研究。

2 工程概况

某中桥跨越规划河道，河道蓝线宽40m，根据规划河道宽度及河道断面形式采用以下桥型方案：上部：2×20m 预应力砼空心板梁；下部：桩柱式墩，轻型薄壁桥台，冲孔灌注桩基础。具体桥型见图1。

图1 桥型立面构造图

3 抗震计算分析

本文主要采用Midas Civil 有限元计算软件对结构进行全桥建模分析计算。与静力分析模型有所不同，抗震计算模型不在于精细地模拟，而重点是要真实、准确地反映桥梁上下部结构、支座和地基的刚度、质量分布及阻尼特性，同时应满足下列要求：

（1）计算模型中的梁体和墩柱可采用空间杆系单元模拟，单元质量可采用集中质量代表；墩柱和梁体的单元划分应反映结构的实际动力特性；

（2）支座单元应反映支座的力学特性；

（3）计算模型应考虑相邻结构和边界条件的影响。

全桥考虑土-下部结构-上部结构的共同协同工作抵抗纵、横桥向地震作用，利用土弹簧模拟桩－土相互作用，真实模拟桩基础并考虑P-△效应。全桥模型见图2。

图2 全桥模型

3.1 振型分析

通过振型分析可以得到桥梁的各项动力特性值，包含振型形状、固有周期、振型参与系数、振型参与质量等。在一般的有限元分析中，由于系统的自由度很多，同时在研究系统的响应时，往往只需要了解少数较低的特征值及相应的特征向量，因此在有限元分析中，发展了一些适应上述特点而效率较高的解法（子空间迭代法、lanczos 和多重Ritz 向量法）。多重Ritz 向量能用于线性和非线性结构的动力分析。与精确特征向量法相比，多重Ritz 向量法用更少的时间可产生更精确的结果。

因此，本模型采用多重Ritz 向量法计算模态，表1 列出了桥梁结构的前18 阶自振频率和周期和振型质量参与系数。用多振型反应谱法计算时，所考虑的振型阶数应在计算方向获得90%以上的有效质量。由表1可知本桥在顺桥向X 向、横桥向Y 向的参与系数总和分别为93.01%、94.05%，满足规范规定要求。

表1 振型计算结果

3.2 反应谱分析

反应谱分析是将多自由度体系视为多个单自由度体系的组合，通过计算各自由度体系的最大地震响应后再进行组合的方式计算多自由度体系的最大地震响应的分析方法。

反应谱分析的动力平衡方程见公式（1）：

式中：M 为质量矩阵，C 为阻尼矩阵，K 为刚度矩阵，u(t)表示相对位移。

反应谱提供了一种方便的手段来概括所有可能的线性单自由度体系对地面运动的某个特定分量的峰值反应。某个反应量的峰值作为体系的固有振动周期Tn的相关参数的函数图形，称为该反应量的反应谱，它是单自由度弹性体系在给定的地震作用下，某个最大反应量（位移、速度、加速度）与体系自振周期的关系曲线。

反应谱分析主要步骤见图3。

图3 反应谱分析步骤图

选取阻尼比为0.05 的水平设计加速度反应谱S，由公式（2）确定。

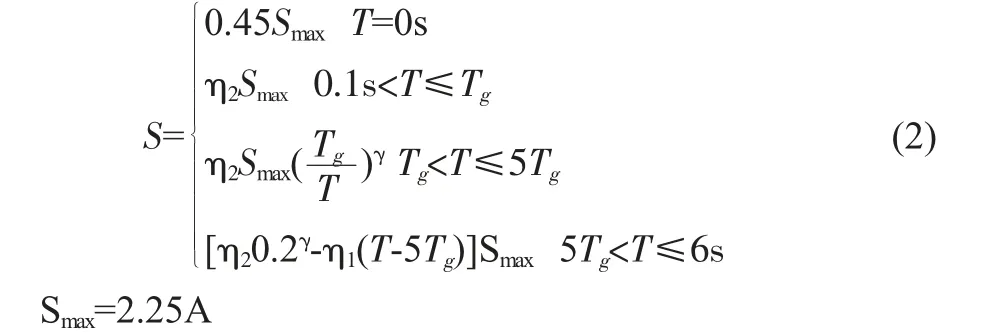
式中：Tg为特征周期，η2为结构的阻尼调整系数，A 为水平向地震动峰值加速度，γ 为曲线衰减指数，η1为下降斜率调整系数，T 为结构自振周期。

桥址处的抗震设防烈度为Ⅶ度，设计基本地震加速度值为0.10g，场地类型为Ⅱ类，场地特征周期为0.4s，本工程抗震设防类别为B 类。根据地震相关设计参数，建立E1、E2 地震作用反应谱函数，见图4 和图5。

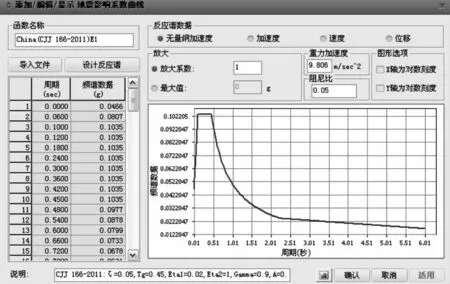
图4 E1 地震作用加速度反应谱

图5 E2 地震作用加速度反应谱

在地震作用下，规则桥梁的柱式墩，采用反应谱方法计算时，其顺桥向水平地震力可采用下列简化公式（3）计算：

式中：Ehtp为作用于支座顶面处的水平地震力，Sh1为相应水平方向的加速度反应频谱，Gt为支座顶面处的换算质点重力。其计算简图见图6。

图6 结构计算简图

用多振型反应谱法计算时，单一方向的地震作用效应（内力、位移）一般可采用SRSS 方法，可按公式（4）计算:

式中：F 为结构的地震作用效应；Si为结构第i 阶振型地震作用效应。

基于Midas Civil 计算结果，根据《公路桥梁抗震设计细则》（JTG/T B02-01-2008）对抗震验算的要求，选取1#桥墩墩顶（单元81）及墩底（单元85）两处不利截面的内力计算结果进行分析。

（1）E1 地震作用桥墩单元强度验算，见表2：

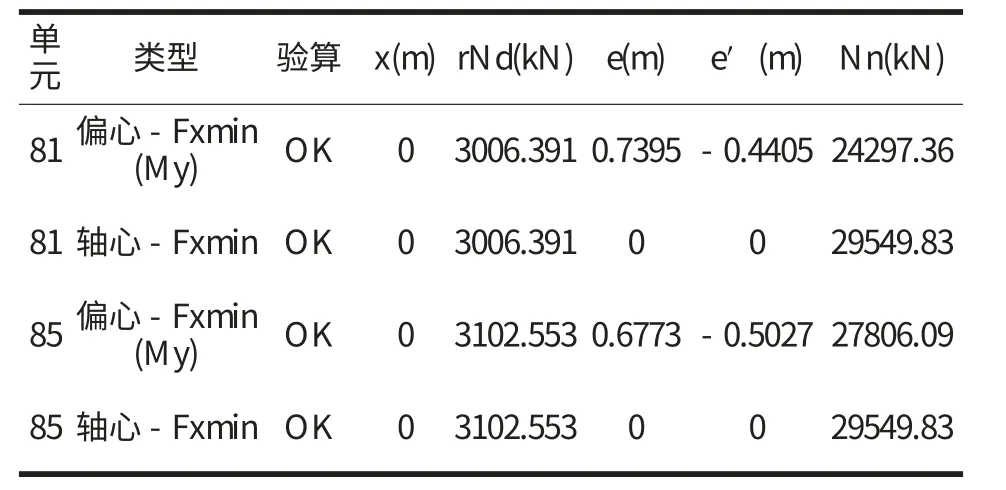
表2 E1 地震作用桥墩单元验算结果

（2）E2 地震作用桥墩单元强度验算，见表3：

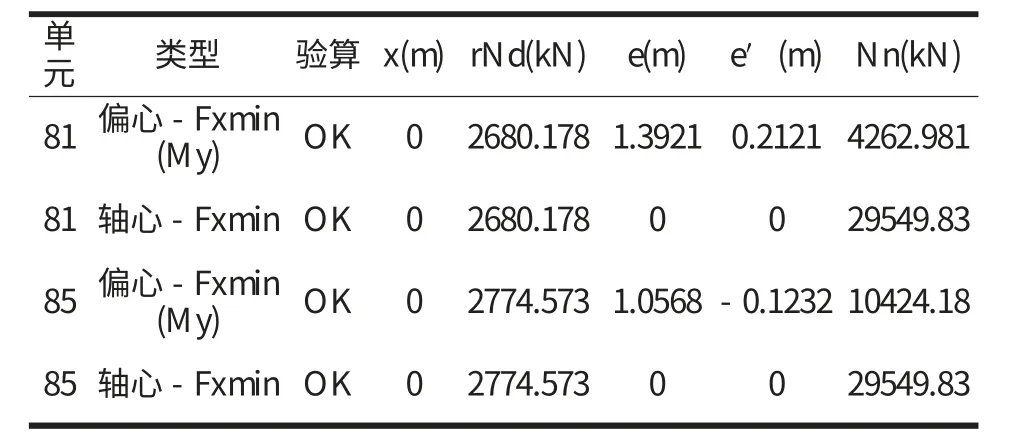
表3 E2 地震作用桥墩单元验算结果

（3）E2 地震作用桥墩塑性铰区抗剪强度验算，见表4：

表4 E2 地震作用桥墩塑性铰区验算结果

（4）E2 地震作用规则桥梁墩顶位移验算，见表5：

表5 E2 地震作用桥墩顶位移验算结果

3.3 时程分析

时程分析方法是先选定地震地面加速度图，然后用数值积分方法求解运动方程，算出每一时间增量的结构反应，如位移、速度和加速度反应。

地震波的选取对结构时程分析的结果较大，因此对地震波的选取非常重要，对于其选取一般有两种做法：一种是对实际地震记录进行修正；另一种是通过一定的方法在大量的实际地震记录中选取一些满足规范要求的地震记录。考虑到地震的随机性，根据抗震设计规范，选择的加速度时程曲线不应少于三组。

动态时程分析法能利用地震波相位差及不同地震波多分量、多点输入等因素建立结构动力计算图式和相应的地震振动方程，能反映地震的强度特性，地震的频谱和持时特点，是结构在某一地震作用下的全程反映。时程荷载函数定义见图7。墩底剪力时程结果见图8。

图7 时程荷载函数定义

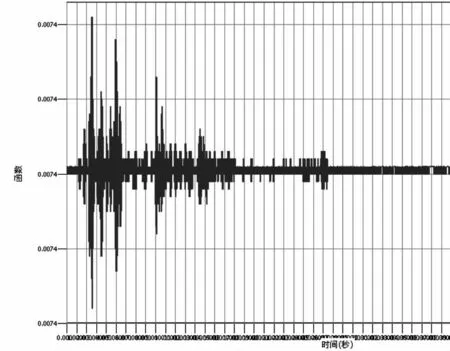
图8 墩底剪力时程结果

4 结论

根据上述不同方法的计算结果，可以得出以下结论：

（1）桥墩顶跟桥墩底是受力最不利的截面，在抗震设计时应特别注意。

（2）E1 地震作用下，桥墩强度满足抗震性能要求。

（3）E2 地震作用下，桥墩纵桥向进入延性，墩顶位移小于墩顶容许位移，满足抗震性能要求，按能力保护构件验算，桥墩纵桥向抗剪满足抗震性能要求。

（4）反应谱分析主要考虑结构周期与地基的卓越周期相近的情况，也就是结构的最大响应。多自由度的时候，在假设经典阻尼的情况下，用SRSS,CSC 等进行振型叠加，其结果是最大位移的叠加，带有一定的保守性。而动力时程分析是先选定地震地面加速度图，然后用数值积分方法求解运动方程，算出每一时间增量的结构反应，但是计算过程复杂。从本文的算例可以看出，反应谱法分析时，在E1 地震作用下，墩底受压强度为3103KN，时程分析计算结果为2726KN,满足规范要求的时程分析结果不小于反应谱法计算结果80%的规定，且从计算结果中我们可以看出反应谱分析下的主要截面的内力值一般比时程分析下的内力值大，因此从理论分析与实际计算中，我们发现对于常规桥梁，采用反应谱法来分析地震作用还是比较简单可靠的。

[1]JTG/T B02-01-2008，公路桥梁抗震设计细则.

[2]CJJ 166-2011，城市桥梁抗震设计规范.

[3]范立础,卓卫东.桥梁延性抗震设计［M］.北京:人民交通出版社，2001.

[4]葛俊颖.桥梁工程软件Midas Civil 使用指南.北京:人民交通出版社，2013.