带随机微缺陷椭圆孔口的应力分析
2015-04-24李兆霞
周 胜 李兆霞
(东南大学土木工程学院, 南京 210096)(东南大学江苏省工程力学分析重点实验室, 南京 210096)
带随机微缺陷椭圆孔口的应力分析
周 胜 李兆霞
(东南大学土木工程学院, 南京 210096)(东南大学江苏省工程力学分析重点实验室, 南京 210096)
利用复变函数方法,构造了保角变换函数,求解了带随机半圆形微缺陷的椭圆孔口应力场.通过分离保角变换函数,得到了微缺陷与宏观椭圆孔口应力场解析解的分离形式.研究结果表明,微缺陷主要对椭圆孔局部应力场产生影响,而对于远离微缺陷区域的应力场则影响较小.当椭圆形状固定时,微缺陷端部的应力集中系数仅与缺陷半径及微缺陷的位置有关;缺陷越小,应力集中系数越大,且此数值远大于无缺陷时椭圆孔口的应力集中系数,说明当孔边带有微缺陷时,尽管缺陷尺度远小于椭圆孔的尺度,但微缺陷对椭圆孔边缘应力集中的影响仍不容忽视.
微缺陷;椭圆孔口;复变函数;尺度分离;应力集中系数
航空航天、机械制造以及土木工程领域中存在着大量的孔口问题.应力场分析可将其简化为椭圆孔口边缘应力场来进行求解.除结构中人为制造的孔口外,很多材料(如混凝土材料和晶体材料等)在成型过程中,材料内部会不可避免地出现一些微孔口.考虑这类微裂纹的作用,求解孔口附近应力场的解析表达式和应力强度因子是非常重要的.
学者们已对工程和材料中的孔口问题进行了大量研究.赵凯等[1]利用复变函数方法研究了岩土工程中矩形硐室问题,采用Schwarz-Christoffel积分方法求取矩形硐室的解;祝江鸿等[2]利用复变函数级数展开方法研究了任意硐室的应力场解答.其他类型的材料在生产过程中也会随机产生微孔口,为简单起见,通常将其简化成圆形或椭圆形孔口,利用复变函数方法进行求解.高存法等[3]研究了含椭圆孔压电材料的解析解;朱西平等[4]研究了含圆孔复合材料板的孔边应力集中系数.利用复变函数方法研究孔口问题时,仅在微孔口尺度下考虑了材料的应力场,并未考虑孔口边缘发生更小尺度缺陷时局部应力集中导致的结构失效[5].
随着复变函数理论及断裂力学的发展,采用复变函数方法处理孔口问题时,引入了非简单的多项式函数来进行求解,极大地拓展了复变函数在不光滑孔口问题上的应用,并在求解带裂纹孔口问题方面取得了较大进展[6-9].郭俊宏等[10-11]分析了长轴处双裂纹椭圆孔口的压电材料问题,研究了准晶体材料的应力场;Hasebe等[12]利用数值方法分析了带裂纹的方形孔口问题;曾芸芸[13]研究了带裂纹的圆形孔口问题;郭怀民等[14]分析了长轴处带裂纹的椭圆孔口问题.但这些研究仅考虑了含宏观裂纹孔口的应力强度因子,并没有考虑含孔口材料裂纹萌生时孔口边缘的随机微缺陷对裂纹萌生和扩展的影响.
在处理复杂孔口时,传统的保角变换方法存在着一定的局限性,无法得到带随机微缺陷椭圆孔口的保角变换函数.本文利用复变函数方法研究了带随机微缺陷的椭圆孔口问题.采用尺度分离方法,构建了2个尺度下分离的保角变换函数,得到了带微缺陷椭圆孔口的应力场解答,为利用传统复变函数方法求解多尺度缺陷的孔口问题提供了理论分析基础,也为处理实际工程和材料中的孔口问题提供了新的思路.
1 带微缺陷椭圆圆孔的保角变换
由文献[6]可知,利用复变函数方法求解复杂孔口的应力场,首先需要构造保角变换函数,将复杂边界映射到简单边界上进行处理.为了得到带微缺陷椭圆孔口的保角变换函数,需要对保角变换函数进行近似变换.
图1为带微缺陷椭圆孔口保角变换过程.首先,根据严格的保角变换形式,将γ平面中单位圆内的区域变换为Z1平面中带缺陷的单位圆外区域;然后,利用近似变换,将Z1平面区域变换为Z平面上带微缺陷的椭圆圆孔.图中,a,b分别为椭圆的长轴和短轴;α,β分别为Z1平面和Z平面上微缺陷中心和圆心连线与x轴之间的夹角.

(a) 无缺陷单位圆孔(γ平面)

(b) 含微缺陷单位圆孔(Z1平面)

(c) 含微缺陷椭圆孔口(Z平面)
含微缺陷的单位圆孔如图1(b)所示.γ平面圆周上ζ=eiα处存在半径为ρ的半圆形微缺陷,且ρ≪1.保角变换函数为
(1)
式中,ω1(ζ)为多值函数.

为准确表达圆孔和微缺陷对最后应力场的影响,可将式(1)改写为
(2)
式中,1/ζ为含圆孔的无限大平面的保角变换函数;δ(ζ,α)为微缺陷的保角变换函数.δ(ζ,α)将数学平面上ζ=e-i α的邻域变换成物理平面上z1=1处的微缺陷,在远离ζ=e-i α的区域,δ(ζ,α)=0.
由文献[6]可知,将单位圆内部映射到含椭圆孔口的无限大平面的保角变换函数为
(3)

可以利用椭圆保角变换函数局部的保圆性来近似构造变换函数,即
(4)
在ζ=e-iα的邻域处,δ(ζ,α)为一微小量.根据保角变换的局部保圆性,在ζ=e-iα的邻域处,ω(ζ)也近似变换为半圆形微缺陷,而在远离ζ=e-iα的区域处,由于δ(ζ,α)=0,根据ω(ζ)可将单位圆变换为无缺陷的椭圆边界.因此,根据式(4)可将γ平面上单位圆内的区域变换为含带圆弧形微缺陷椭圆孔口的无限大平面.
利用级数展开公式可以得到
(5)
δ(ζ,α)相对于ζ为小量,将式(5)代入式(4)并略去δ(ζ,α)2以上的高阶项,可将式(4)简化为
z=ω(ζ)=ω0(ζ)+R(1-mζ2)δ(ζ,α)
(6)
在远离ζ=e-iα的邻域处,δ(ζ,α)=0,且表达式R(1-mζ2)在单位圆内有界.如果椭圆局部曲率变化较小,可将式(6)简化为
z=ω(ζ)=ω0(ζ)+Kδ(ζ,α)
(7)
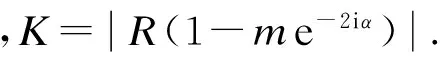

根据保角变换函数,可以求得β与α的关系,即
2 带微缺陷椭圆孔口的解析解
无限大孔口的力学问题通常采用复变函数方法进行求解.孔口问题的应力场可以通过2个应力函数φ(ζ)和ψ(ζ)获得.φ(ζ)和ψ(ζ)满足如下方程:
(8)
(9)
式中
(10)
(11)
(12)

由式(4)可得
(13)

(14)
H(σ)可以延拓为圆周上的连续函数,且H(∞)=0,故
为简单起见,可以设含带微缺陷圆孔的无限平面孔口边缘不受力,仅在无穷远处受到与y轴平行的大小为q的均布拉应力.根据式(10)可知
(15)
由于δ(ζ)在单位圆内除了ζ=0外处处解析,且ζ=0为δ(ζ)的可去奇点,故δ(ζ)在单位圆内可表示为
(16)
式中,bn(α)为与α相关的复常数.
根据Cauchy积分原理,可以得到
(17)
同理可求得
(18)
最后,根据式(8)和(9)可以求得
(19)
(20)
令Φ(ζ)=φ′(ζ)/ω′(ζ),Ψ(ζ)=ψ′(ζ)/ω′(ζ),则可以求得含带微缺陷椭圆孔口的无限大平面的应力场公式为
σθ+σρ=4ReΦ(ζ)
(21)
(22)
式中,σθ,σρ和τρθ分别表示极坐标下的环向应力、径向应力和切应力.
3 应力场分析
对于孔口问题而言,孔口边缘的应力集中系数与材料失效密切相关.当椭圆孔口边缘出现微缺陷时,缺陷端部为应力集中区.利用式(21),可以求出ρ≠0时椭圆孔口边缘缺陷的应力集中系数η.

(23)
当a=2,b=1时,微缺陷应力集中系数η与微缺陷半径r的关系曲线见图2.由图可知,当含带微缺陷椭圆孔口的无穷大平面在无穷远处承受垂

图2 微缺陷半径与应力集中系数的关系
直于长轴的均布载荷时,微缺陷的应力集中系数与微缺陷半径成反比,随着缺陷半径的减小,应力集中系数逐渐增加.当r足够小时,应力集中系数趋近于3+4a/b.根据已知的无缺陷椭圆孔口长轴处应力集中系数η′=1+2a/b,当椭圆孔口长轴存在半圆形微缺陷时,微缺陷应力集中系数最大值ηmax=1+2η′.
当b=1时,微缺陷应力集中系数与微缺陷位置之间的关系曲线如图3所示.由图可知,当微裂纹出现在长轴(即β=0)时,应力集中系数最大;随着β的增大,应力逐渐变小.a/b越大,应力集中系数的最大值也越大;β越大,应力集中系数衰减得越快.
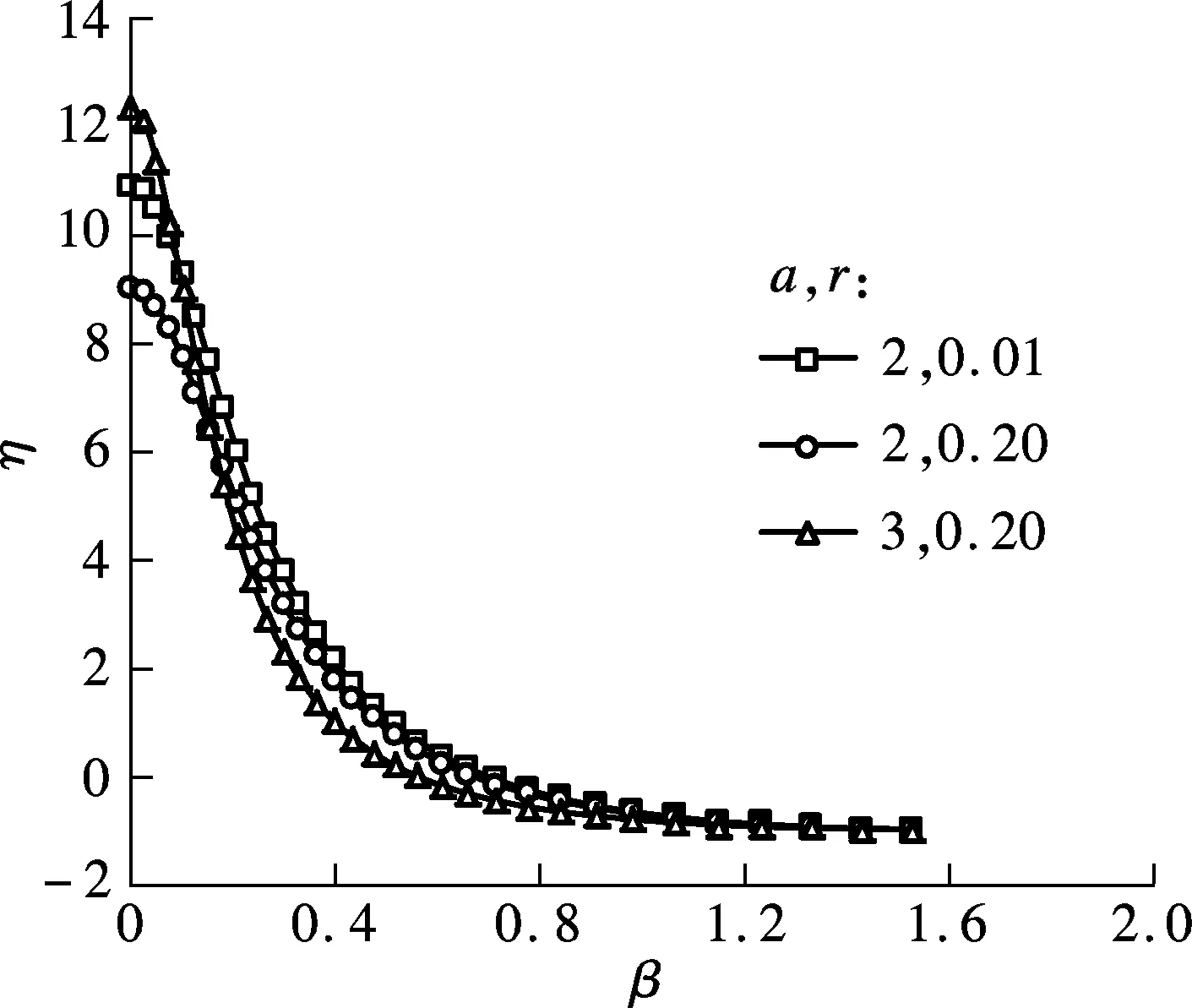
图3 微缺陷应力集中系数与微缺陷位置之间的关系图
4 结语
本文通过建立含带随机微缺陷椭圆孔口的无限大平面分析模型,解决了工程中普遍存在的带随机微缺陷孔口的应力场求解问题.利用针对局部微缺陷的尺度分离方法,得到了复合保角变换表达式.利用保角变换的局部保角性,扩展了复变函数方法的应用范围.研究结果表明,椭圆孔口边缘产生的微缺陷会对微缺陷附近局部应力产生影响,但对微缺陷远端区域的应力影响较小.微缺陷的产生导致缺陷端部出现应力集中现象,应力集中系数与缺陷半径有关,微缺陷半径越小,应力集中系数越大.当微缺陷出现在长轴位置时,应力集中系数最大,且最大值随着微缺陷半径的减小逐渐趋近于3+4a/b.
References)
[1]赵凯, 刘长武, 张国良.用弹性力学的复变函数法求解矩形硐室周边应力[J]. 采矿与安全工程学报, 2007, 24(3): 361-365. Zhao Kai, Liu Changwu, Zhang Guoliang. Solution for perimeter stresses of rocks around a rectangular chamber using the complex function of elastic mechanics[J].JournalofMining&SafetyEngineering, 2007, 24 (3):361-365.(in Chinese)
[2]祝江鸿, 杨建辉, 施高萍,等. 单位圆外域到任意开挖断面隧洞外域共形映射的计算方法[J]. 岩土力学, 2014,35 (1): 175-183. Zhu Jianghong, Yang Jianhui, Shi Gaoping, et al. Calculating method for conformal mapping from exterior of unit circle to exterior of cavern with arbitrary excavation cross-section [J].RockandSoilMechanics, 2014, 35 (1): 175-183.(in Chinese)
[3]高存法, 董登科. 含椭圆孔压电材料平面问题的复变函数解[J]. 工程力学,1998,15(3):98-104. Gao Cunfa, Dong Dengke. The complex functions for plane problems of piezoelectric material with an elliptical hole[J].EngineeringMechanics, 1998, 15(3): 98-104.(in Chinese)
[4]朱西平,郭章新,韩小平,等. 含孔复合材料层合板孔边应力集中的近似计算[J]. 航空材料学报, 2009,29(2):71-75. Zhu Xiping, Guo Zhangxin, Han Xiaoping, et al. Approximate calculation of stress distribution near hole for composite laminates with finite width[J].JournalofAeronauticalMaterials, 2009, 29 (2):71-75.(in Chinese)
[5]Wu Hwai-Chung, Mu Bin. On stress concentrations for isotropic/orthotropic plates and cylinders with a circular hole[J].CompositesPartB:Engineering, 2003, 34(2): 127-134.
[6]Erdogan F. Stress intensity factors [J].JournalofAppliedMechanics, 1983, 50(4):992-1002.
[7]Shen D, Fan T. Exact solutions of two semi-infinite collinear cracks in a strip [J].EngineeringFractureMechanics, 2003, 70(6): 813-822.
[8]Sih G C. Stress distribution near internal crack tips for longitudinal shear problems [J].JournalofAppliedMechanics, 1965, 32(1): 51-581.
[9]陈柱, 刘官厅, 关璐. 星形裂纹的应力分析[J]. 力学学报, 2009, 41(3): 425-430. Chen Zhu, Liu Guanting, Guan Lu. Stress analysis of star cracks [J].ChineseJournalofTheoreticalandAppliedMechanics, 2009, 41(3): 425-430.(in Chinese)
[10]郭俊宏,刘官厅.带双裂纹的椭圆孔口问题的应力分析[J].力学学报,2007,39(5):699-703. Guo Junhong, Liu Guanting. Stress analysis for an elliptical hole with two straight-cracks [J].ChineseJournalofTheoreticalandAppliedMechanics, 2007,39 (5):699-703. (in Chinese)
[11]Guo Junhong, Liu Guanting. Exact analytic solutions for an elliptic hole with asymmetric collinear cracks in a one-dimensional hexagonal quasi-crystals[J].ChinesePhys, 2008, 17(7): 2610-2620.
[12]Hasebe N, Nakamura T, Yoshikawa K, et al. Plane elastic solution for the second mixed boundary value problem and its application [J].ArchiveofAppliedMechanics, 1994, 64(5): 295-306.
[13]曾芸芸. 圆弧裂纹问题的复变函数方法研究 [D]. 北京:北京理工大学数学系,2006.
[14]郭怀民,刘官厅,皮建东.带裂纹的椭圆孔口问题的应力分析[J].固体力学学报,2007,28(3):308-312. Guo Huaimin, Liu Guanting, Pi Jiandong. Stress analysis of anellipse hole with a straightedge-crack by complex variable method [J].ActaMechanicaSolidaSinica, 2007, 28(3): 308-312.(in Chinese)
Analysis on stresses of elliptical hole with random micro-defect
Zhou Sheng Li Zhaoxia
(School of Civil Engineering, Southeast University, Nanjing 210096, China)(Jiangsu Key Laboratory of Engineering Mechanics, Southeast University, Nanjing 210096, China)
The conformal mapping function is constructed and the stress field of an elliptical hole with a random semicircular micro-defect is solved by using the complex function method. The separation form of the analytical solution of the stress field for the small-scale defect and the circular hole can be obtained through splitting the conformal function. The results show that the micro-defect mainly affects on the local stress field around the elliptical hole, and the influence on the zone away from the small-scale defect is small. When the ellipse shape is fixed, the stress concentration factor only depends on the curvature radius and the position of the defect. The smaller the defect, the greater the stress concentration factor. Moreover, the stress concentration factor of the micro-defect is much greater than that of an ellipse without micro-defects. This suggests that when there is a semicircular micro-defect on an elliptical hole edge, the influence of the micro-defect on stress concentration nearby the elliptical hole cannot be ignored even though the scale of the defect is far smaller than that of the ellipse.
micro-defect;elliptical hole;complex function;scale separation;stress concentration factor
10.3969/j.issn.1001-0505.2015.02.025
2014-09-20. 作者简介: 周胜(1987—),男,博士生; 李兆霞(联系人),女,博士,教授,博士生导师, zhxli@seu.edu.cn.
国家自然科学基金资助项目(11072060).
周胜,李兆霞.带随机微缺陷椭圆孔口的应力分析[J].东南大学学报:自然科学版,2015,45(2):343-347.
10.3969/j.issn.1001-0505.2015.02.025
O346.1
A
1001-0505(2015)02-0343-05
