等强度砂浆下低收缩胶凝材料的优化设计

周 宁 钱春香 何智海

(1东南大学材料科学与工程学院, 南京 211189)(2 绍兴文理学院土木工程学院, 绍兴 312000)

等强度砂浆下低收缩胶凝材料的优化设计

周 宁1钱春香1何智海2

(1东南大学材料科学与工程学院, 南京 211189)(2绍兴文理学院土木工程学院, 绍兴 312000)

为了快速优化设计低收缩胶凝材料,根据不同的胶凝材料组合制备了强度相近的胶砂,基于灰色系统理论选择与胶砂收缩关联度较大的因素作为影响因素，建立了胶砂收缩GM(1,N)模型．结果表明:C-S-H与未水化颗粒的体积比、变形抵抗因子和砂浆强度与胶砂收缩的关联度较大,其关联度分别为0.759,-0.678和-0.631．以此建立的胶砂收缩GM(1,4)模型模拟精度较高,可靠性较好,其平均相对误差为8.96%,全部收缩模拟值的相对误差小于15%左右．该模型中的主要影响因素易获取,其试验方法简单实用,可操作性强,减少了繁琐的试验．

收缩;灰色理论;关联度;GM(1,N)模型

自19世纪首次发现混凝土的收缩问题以来,世界各国已得出了许多干燥收缩的经验公式,如美国ACI209委员会提出的ACI式[1]、欧洲的CEB式[2]以及Bazant和Panula提出的BP式[3]等．而在我国目前采用中国建筑科学研究院《混凝土收缩与徐变试验研究》专题协作组提出的多函数方程进行计算[4]．上述公式均是在大量试验数据基础上提炼的经验公式,其预测精度受到测定误差的影响,而且公式仅考虑水泥部分的影响,忽视了矿物掺合料的影响．在水泥基材料发展的今天,建立在已往测试结果上的收缩预测经验公式显然无法适用于大掺量矿物掺合料高性能水泥基材料．

灰色系统理论建模是一种少数据、动态信息开发、利用和加工优化的微分方程建模方式,其中GM模型是其基本模型．为此,本文基于强度相近的不同胶凝材料组合制备了胶砂,应用灰色系统理论,选择与收缩关联度较大的因素作为影响因素,通过少量有限的实验数据建立GM(1,N)收缩预测模型．最终在给定原材料的条件下,快速选择具有低收缩性质的胶凝材料作为最佳组合方式,使试验方案设计有依据,减少了试验量．

1 试验

1.1 原材料

采用江南小野田水泥厂生产的P·Ⅱ 42.5水泥,其比表面积为350 m2/kg,表观密度为3 120 kg/m3．选用电厂干排粉煤灰,其中一级粉煤灰取自浙江宁波,其比表面积为550 m2/kg,表观密度为2 340 kg/m3,二级粉煤灰取自南京热电厂,其比表面积为380 m2/kg,表观密度为2 180 kg/m3．采用南京华强矿粉厂的矿渣粉,其比表面积为420 m2/kg,表观密度为2 850 kg/m3．惰性掺合料分别采用纯度大于90%的石灰石粉、石英砂粉和金刚砂粉,其比表面积分别为550,750和880 m2/kg．各原材料的化学组成见表1．为简便起见,将P·Ⅱ 42.5水泥、一级粉煤灰、二级粉煤灰、矿渣粉、石灰石粉、石英砂粉、金刚砂粉分别记为C,FAⅠ,FAⅡ,S95,LP,QP,EP．

本课题组对胶凝材料颗粒进行纳米压痕测试,其弹性模量见表2[5]．

表1 原材料的化学组成 %

注:R2O为碱金属氧化物.

表2 胶凝材料颗粒的弹性模量 GPa

1.2 试验方法

1.2.1 试样制备

根据表3制备40,45,55 MPa三种不同强度等级、但强度相近的砂浆,各组胶砂的胶凝材料和标准砂用量分别为450和1350 g.根据不同的水胶质量比决定用水量,通过调整减水剂使胶砂保持相近的流动度,试件的成型、养护和强度测定均按《水泥胶砂强度检验方法(ISO法)》(GB/T 17671—1999)[6]进行．

表3 不同强度等级砂浆的试验配合比

1.2.2 反应程度的测定

1) 粉煤灰和矿渣粉反应程度

取适量硬化浆体压碎,在异丙醇中浸泡25 min,然后在装有无水乙醇的研钵中磨细至全部通过0.08 mm筛,真空吸滤.过滤后的粉状样品在预先放置钠石灰的真空干燥箱中于80～200 kPa压力和105 ℃下干燥24 h,之后根据《水泥组分的定量测定》(GB/T 12960—2007)[7]盐酸选择性溶解法测试粉煤灰反应程度αF，采用文献[8]中的EDTA选择性溶解法，测试矿渣粉反应程度αS．

2) 水泥水化程度

依据Powers模型,纯水泥浆中水泥水化程度可采用下式计算:

(1)

式中,αC为水泥的水化程度;Wn为单位质量纯水泥浆体的化学结合水含量,%．

根据Lam等[9]和张云升等[10]提出的纯水泥水化程度与水灰比的回归方程

(2)

通过测试不同水灰比28 d龄期的纯水泥水化程度得出试验回归常数a和b．式中,w和c分别为用水量和复合体系中水泥用量．

在上述试验和计算的基础上,把原来的水灰比替换成考虑矿物掺合料影响的有效水胶比,即可得复合体系的水泥水化程度，即

(3)

式中,mMA为复合体系中矿物掺合料用量;αMA为矿物掺合料在复合浆体中的反应程度．

1.2.3 胶砂收缩的测定

胶砂成型后,根据《水泥胶砂干缩实验方法》(JC/T 603—2004)[11]对胶砂进行28 d收缩值的测定．

2 结果与分析

2.1 胶砂收缩影响因素的灰色关联分析

影响胶砂收缩的影响因素很多,在此选取胶砂强度、胶凝材料变形抵抗因子、C-S-H体积含量、未水化颗粒体积含量、C-S-H与未水化颗粒体积比、胶凝材料烧失量、CaO含量、胶凝材料堆积密度和表观密度等影响因素,然后采用灰色关联分析得出其中的主要影响因素,为后续的胶砂收缩设计模型提供相应的参数．

2.1.1 C-S-H与未水化颗粒体积比

水泥基材料是一种多相复合材料,主要有胶结能力的变形相C-S-H和抵抗变形的约束相未水化胶凝材料颗粒组成,C-S-H与未水化颗粒体积比是影响收缩的一个重要影响参数．

1) 水泥水化产生的C-S-H[5,12]

水泥水化产生的C-S-H计算公式为

mC,C-S-H=171(nC2S+nC3S)αCfC

(4)

式中,mC,C-S-H为水泥水化产生的C-S-H质量;fC为水泥在复合体系中的质量分数,%;nC2S和nC3S分别为硅酸二钙和硅酸三钙摩尔数．

2) 矿物掺合料活性效应产生的C-S-H[13-16]

矿物掺合料活性效应产生的C-S-H计算公式为

(5)

式中,mMA,C-S-H为矿物掺合料活性效应产生的C-S-H质量;fS,MA,i为复合体系中每种矿物掺合料化学组成氧化硅的质量分数,%;fMA,i为每种矿物掺合料在复合体系中的质量分数,%;αMA,i为每种矿物掺合料在复合浆体中的反应程度．

由式(5)得出复合体系水化反应产生的C-S-H为

mC-S-H=mMA,C-S-H+mC,C-S-H

(6)

式中,mC-S-H为复合体系水化反应产生的C-S-H质量．

根据复合材料理论,复合材料的各组分相对比例对材料性能的影响比各组分绝对含量的影响大．因此研究胶砂相应浆体C-S-H与未水化颗粒体积比对复合体系性能的影响意义更大,在综合上述试验和分析结果的基础上，得到如下计算公式[2]:

(7)

式中,VR为C-S-H与未水化颗粒体积比;ρC-S-H,ρC和ρMA,i分别为C-S-H、水泥和矿物掺合料的表观密度,g/cm3．

根据式(7)可以得到在基于不同强度等级的胶砂情况下,各组胶砂的C-S-H与未水化颗粒体积比和胶砂28 d收缩值之间的关系,如图1所示．

对影响因素进行灰色关联计算,C-S-H与未水化颗粒体积比因素与胶砂28 d收缩值的灰色关联值为0.759,极性为正,由于灰度值较大,因此可选择此参数作为主要影响因素．由图1可知,在胶砂强度相近的情况下,胶凝材料体系的C-S-H与未水化颗粒体积比越大,表明其变形相的含量相对越多,变形抵抗相的含量相对越少,胶砂28 d收缩越大,两者呈正相关的关系,这一点与灰色关联分析计算的结果相一致(极性为正)．

2.1.2 变形抵抗因子

根据复合材料理论,变形抵抗因子是胶凝材料各组成材料在该胶凝体系中所占体积率与其自身的纳米弹性模量乘积的代数和,另外部分胶凝材料水化使其不再起抵抗变形的作用,因此最终的抵抗因子必须考虑胶凝材料的反应程度[2]．变形抵抗因子主要受胶凝材料堆积密度和纳米弹性模量影响,其值越大,表示抵抗变形的能力越强,如图2所示．

图2 胶凝材料变形抵抗因子示意图

变形抵抗因子的实验和计算步骤如下:

① 计算胶凝材料空隙率.测试胶凝材料的堆积密度和表观密度,从而计算出胶凝材料的空隙率，即

(8)

式中,VC为胶凝材料空隙率;ρBD和ρAD分别为胶凝材料堆积密度和表观密度,g/cm3．

② 计算胶凝材料体积和其之间空隙体积之和.通过测试组成胶凝材料的水泥和矿物掺合料的表观密度，得出其胶凝材料体积,再结合空隙率得出胶凝材料体积和其之间空隙体积之和,即

(9)

式中,TV为胶凝材料体积和其之间空隙体积之和．

③ 考虑反应程度的胶凝材料抵抗因子，即

(10)

式中,RF为胶凝材料抵抗因子,GPa;EC和EMA,i分别为水泥和每种矿物掺合料的纳米弹性模量,GPa．

由此可见,通过调整胶凝材料的组成、掺量和密实堆积程度都可以改变其变形抵抗因子．根据式(8)～(10)可以得到,在基于不同强度等级的胶砂情况下,各组胶砂的变形抵抗因子与胶砂28 d收缩值之间的关系,如图3所示．

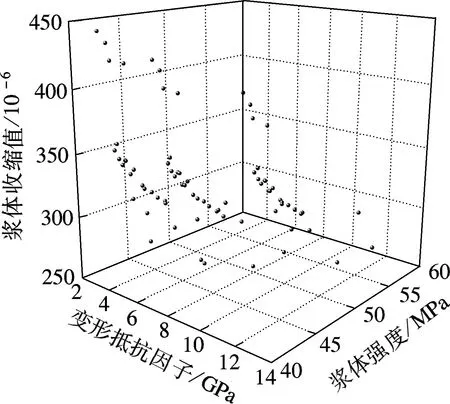
图3 变形抵抗因子与胶砂收缩的关系

对影响因素进行灰色关联计算,变形抵抗因子因素与胶砂28 d收缩值的灰色关联值为0.678,极性为负,由于灰度值较大,因此选择此参数作为主要影响因素．由图3可知,在胶砂强度相近的情况下,总体上胶凝材料体系的变形抵抗因子越大,表明体系中抵抗变形相的含量越多,胶砂28 d收缩值越小,两者呈负相关的关系,这一点与灰色关联分析计算的结果一致(极性为负)．

2.1.3 胶砂强度

在基于不同强度等级的胶砂情况下,各组胶砂的28 d强度与胶砂28 d收缩值之间的关系见图4．

对影响因素进行灰色关联计算,胶砂强度因素与胶砂28 d收缩值的灰色关联值为0.631,极性为负．由于灰度值较大,因此选择此参数作为主要影响因素．由图4可知,对于不同强度等级的胶砂,总体上胶砂28 d强度越大,表明其水胶比越低,单位用水量较少,胶砂28 d收缩越小,两者呈负相关的关系,这一点与灰色关联分析计算的结果相一致(极性为负)．同时,对于不同强度等级的胶砂,各组胶砂的28 d收缩大小排列顺序基本保持不变．

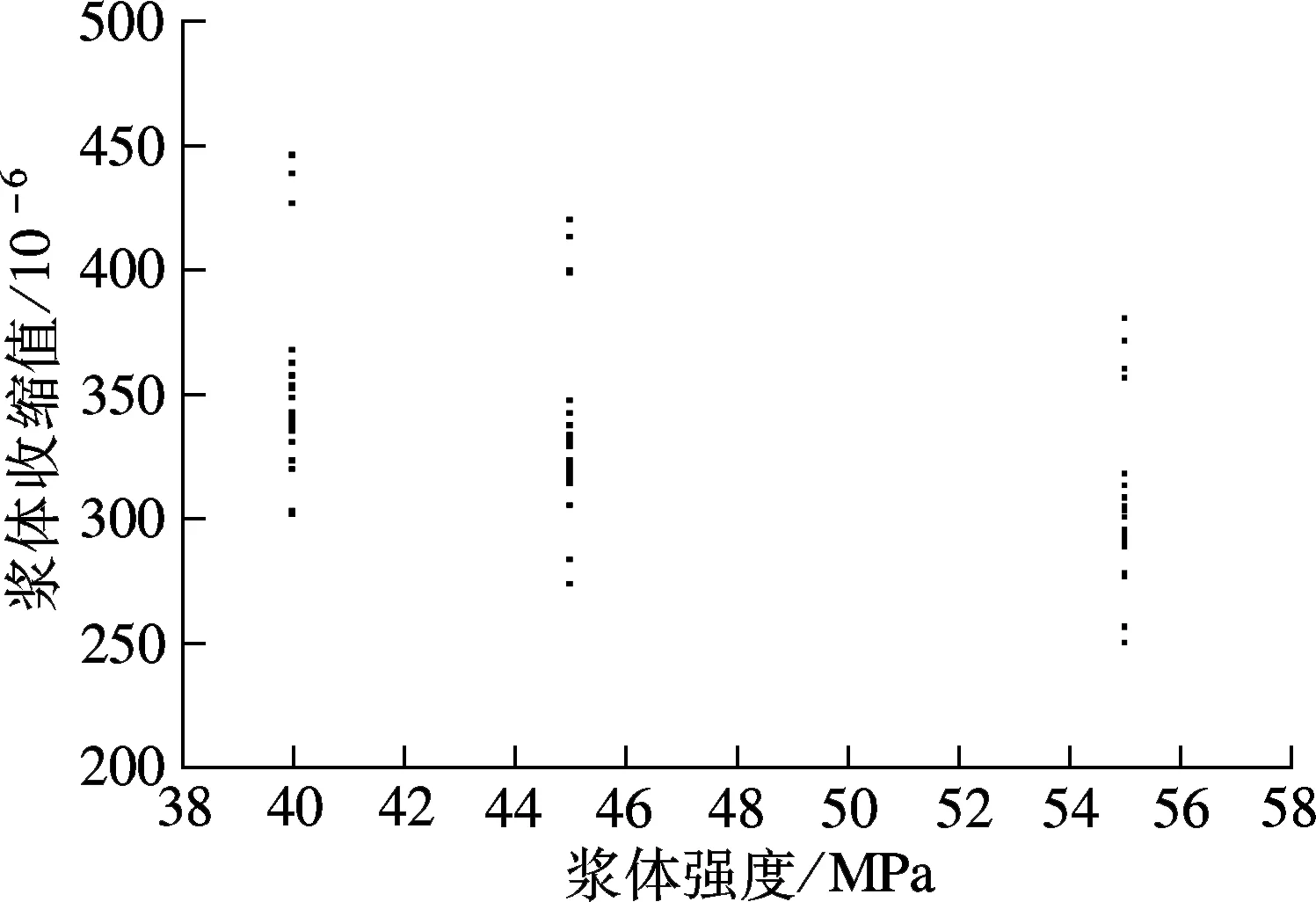
图4 胶砂28 d强度与胶砂收缩的关系

2.2 胶砂收缩GM(1,N)模型的建立

在上述影响因素的灰色关联度分析中,选取灰色关联度较大的影响因素．以胶砂28 d收缩试验结果作为系统特征数据的母序列,相对应的灰色关联度较大的影响因素作为相关因素子序列,从而建立胶砂收缩GM(1,N)模型．

表4 胶砂收缩GM(1, 4)模型的计算参数

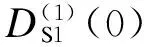
据此可得到胶砂收缩GM(1, 4)模型的累减还原式为

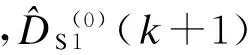
由胶砂收缩GM(1, 4)模型得到的胶砂收缩预测值与试验值对比(见图5)．

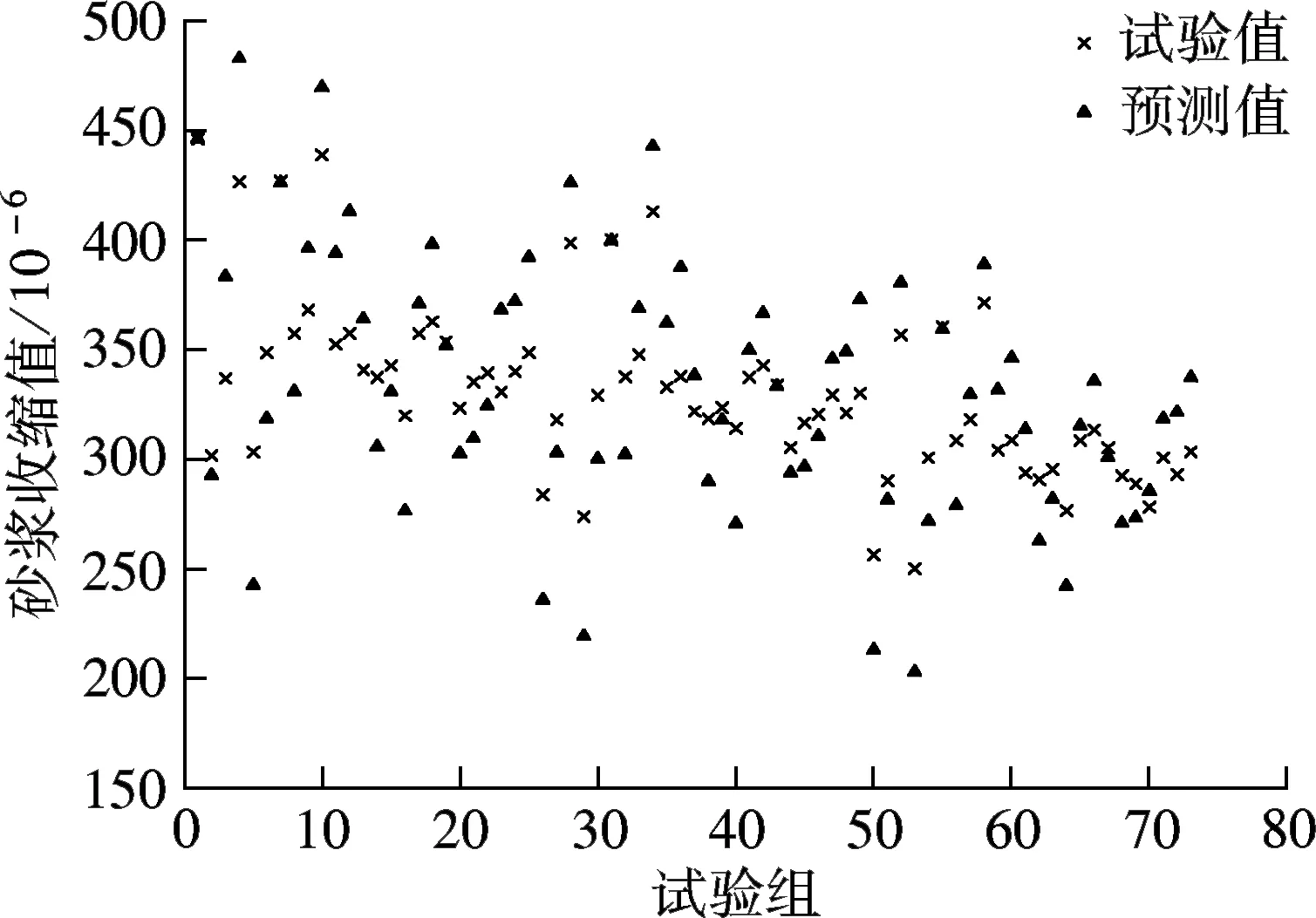
(a) 预测值和试验值对比

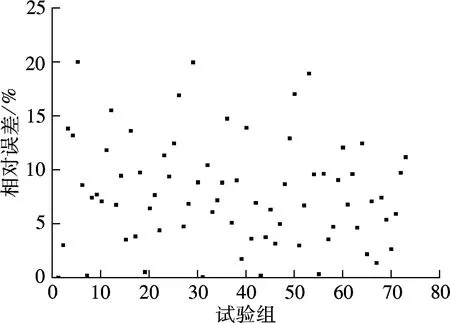
(b) 预测值的相对误差

图5(a)中同一编号胶砂的28 d收缩试验值与预测值在同一条竖直线上,其中的间距即为试验值与预测值的残差．根据图5(a)的残差，可得到图5(b)中75组胶砂收缩试验值与预测值间的平均相对误差(8.96%),胶砂28 d收缩预测值的相对误差小于15%左右,并且胶砂28 d收缩试验值的变化趋势与预测值的变化趋势大体一致,模拟精度较好．试验表明，单掺粉煤灰比单掺矿渣粉更有利于减少胶砂的收缩．当粉煤灰或矿渣粉加入细小的惰性掺合料时,其形成的胶砂28 d收缩值小于单掺粉煤灰或矿渣粉的胶砂28 d收缩值,也小于双掺粉煤灰和矿渣粉的胶砂28 d收缩值．

3 结论

1) 以C-S-H与未水化颗粒体积比、变形抵抗因子和胶砂强度3个主要影响收缩的参数为相关因素子序列,28 d收缩值为系统特征数据母序列,建立的胶砂收缩GM(1, 4)模型模拟精度较高,可靠性较好,其平均相对误差为8.96%,全部收缩模拟值相对误差总体上小于15%左右．

2) 胶砂收缩GM(1, 4)模型实现了通过简单的胶凝材料性能试验即可预测出强度相近的不同胶凝材料组合28 d收缩值,从而优选出低收缩胶凝材料组合,该方法简单实用．

References)

[1]ACI Committee 209. Prediction of creep, shrinkage, and temperature effects in concrete structures [J].ACISpecialPublication, 1982, 76: 193-300.

[2]Gillilan J A. Thermal and shrinkage effects in high performance concrete structures during construction [D]. Calgary: University of Calgary, 2000.

[3]Bazant Z P, Panula L. Practical prediction of time-dependent deformations of concrete [J].MaterialsandStructures, 1978, 11(5): 317-328.

[4]王铁梦. 工程结构裂缝控制 [M].北京:中国建筑工业出版社,1997:1-10.

[5]何智海.低徐变混凝土胶凝材料设计方法及工程应用 [D].南京:东南大学材料科学与工程学院,2013.

[6]全国水泥标准化技术委员会.GB/T 17671—1999水泥胶砂强度检验方法(ISO法) [S].北京:中国标准出版社,1999.

[7]全国水泥标准化技术委员会.GB/T 12960—2007水泥组分的定量测定 [S].北京:中国标准出版社,2007.

[8]郑克仁,孙伟,贾艳涛,等.水泥-矿渣-粉煤灰体系中矿渣和粉煤灰反应程度测定方法 [J].东南大学学报:自然科学版, 2004, 34(3):361-365. Zheng Keren, Sun Wei, Jia Yantao, et al. Method to determine reaction degrees of constituents in hydrating ternary blends composed of BFS, FA and Portland cement [J].JournalofSoutheastUniversity:NaturalScienceEdition,2004, 34(3):361-365. (in Chinese)

[9]Lam L, Wong Y L, Poon C S. Degree of hydration and gel/space ratio of high-volume fly ash/cement systems [J].CementandConcreteResearch, 2000, 30(5): 747-756.

[10]张云升,孙伟,郑克仁,等.水泥-粉煤灰浆体的水化反应进程 [J].东南大学学报:自然科学版, 2006,36(1):118-123. Zhang Yunsheng, Sun Wei, Zheng Keren, et al. Hydration process of Portland cement-fly ash pastes [J].JournalofSoutheastUniversity:NaturalScienceEdition, 2006, 36(1):118-123. (in Chinese)

[11]全国水泥标准化技术委员会.JC/T 603—2004水泥胶砂干缩试验方法 [S].北京:中国建材工业出版社,2005.

[12]李响,阎培渝,阿茹罕.基于Ca(OH)2含量的复合胶凝材料中水泥水化程度的评定方法 [J]. 硅酸盐学报,2009,37(10):1597-1601. Li Xiang, Yan Peiyu, Aruhan. Assessment method of hydration degree of cement in complex binder based on the calcium hydroxide content [J].JournaloftheChineseCeramicSociety, 2009, 37(10):1597-1601. (in Chinese)

[13]Siddique R, Klaus J. Influence of metakaolin on the properties of mortar and concrete: a review [J].AppliedClayScience, 2009, 43(3/4): 392-400.

[14]Sabir B B, Wild S, Bai J. Metakaolin and calcined clays as pozzolans for concrete: a review [J].Cement&ConcreteComposites, 2001, 23(6):441-454.

[15]Bentz D P, Jensen O M, Coats A M, et al. Influence of silica fume on diffusivity in cement-based materials Ⅰ: experimental and computer modeling studies on cement pastes [J].CementandConcreteResearch, 2000, 30(6):953-962.

[16]Papadakis V G. Effect of fly ash on Portland cement systems part Ⅰ: low-calcium fly ash [J].CementandConcreteResearch, 1999, 29(11): 1727-1736.

Optimal design of low shrinkage cementitious materials with equal mortar strength

Zhou Ning1Qian Chunxiang1He Zhihai2

(1School of Materials Science and Engineering, Southeast University, Nanjing 211189, China)(2College of Civil Engineering, Shaoxing University, Shaoxing 312000, China)

In order to quickly optimize the design of low shrinkage cementitious materials, the mortar which has the similar strength was prepared according to different cementitious materials. Based on the gray system theory, the mortar shrinkage GM (1,N) model which selected the factors associated greatly with mortar shrinkage was established. The results show that the volume ratio between C-S-H and unhydrated particle, the deformation resistance factor and the mortar strength have greater correlation with mortar shrinkage, and the correlation factors are 0.759,-0.678 and-0.631, respectively. The mortar shrinkage GM (1,4) model has high simulation accuracy and good reliability. The average relative error is 8.96% and the overall relative error is less than about 15%. The main influence factors of the model are obtained easily and the test method is simple and workable with less tedious trial.

shrinkage; grey theory; correlation; GM(1,N) model

10.3969/j.issn.1001-0505.2015.02.033

2014-09-04. 作者简介: 周宁(1988—),男,硕士生;钱春香(联系人),女,博士,教授,博士生导师,cxqian@seu.edu.cn.

东南大学和瑞士西卡公司合作资助项目．

周宁,钱春香,何智海.等强度砂浆下低收缩胶凝材料的优化设计[J].东南大学学报:自然科学版,2015,45(2):387-392.

10.3969/j.issn.1001-0505.2015.02.033

TU528

A

1001-0505(2015)02-0387-06