肿瘤放疗并发症概率预测模型参数拟合方法

朱 健 白 曈 李宝生舒华忠 Antoine Simon Renaud de Crevoisier

(1东南大学影像科学与技术实验室, 南京 210096)(2山东省肿瘤防治研究院, 济南 250117)(3雷恩第一大学信号与图像实验室, 法国雷恩 35510)

肿瘤放疗并发症概率预测模型参数拟合方法

朱 健1,2白 曈2李宝生1,2舒华忠1Antoine Simon3Renaud de Crevoisier3

(1东南大学影像科学与技术实验室, 南京 210096)(2山东省肿瘤防治研究院, 济南 250117)(3雷恩第一大学信号与图像实验室, 法国雷恩 35510)

为了建立具有群体特异性的肿瘤放疗NTCP预测模型,提出了一种模型参数拟合方法.首先,基于NTCP模型的特点构建最大似然函数;然后,分别采用确定性优化方法和随机性优化方法对最大似然函数进行优化,分析优化过程的时间成本及优化结果,探讨用于拟合NTCP模型参数的最优方法.实验结果表明,用于拟合NTCP模型参数的最大似然函数是非凸的,存在局部最优解;遗传算法是一种最稳定的最大似然函数优化方法,其运行时间比模拟退火算法短,而且可以在每次优化结束后给出全局最优解,以作为NTCP模型参数.所提方法可以帮助肿瘤放疗工作者在临床随访数据的基础上建立具有群体特异性的放疗并发症预测模型.

肿瘤;放射治疗;并发症;NTCP模型

正常组织并发症概率(normal tissue complication probability, NTCP)模型是建立在放疗中剂量-体积关系上的一种数学模型.该模型可以通过调整参数来描述不同器官在接受一定剂量照射后出现放疗并发症的概率,从而对放疗毒性反应进行预测[1-3],也可根据模型预测结果对不同的治疗方案进行生物效应量化对比[4-6].选取模型对放疗并发症进行预测前,需要对NTCP模型进行建模,根据所适用的患者群体出现并发症的随访数据,来拟合具有群体特异性的NTCP模型参数[7].据笔者所知,目前国内外文献未见针对NTCP建模方法的介绍.鉴于此,本文提出了一种针对NTCP模型的拟合方法.首先,构建出最大似然函数;然后,设计实验以寻找最优的参数拟合方法.

1 最大似然函数的构建

采用最大似然估计法来拟合NTCP模型参数.最大似然估计法是一种统计方法,用于求解样本集中相关概率密度函数的参数.给定一个概率分布D,其概率密度函数(连续分布)或概率聚集函数(离散分布)为fD.从该分布中抽出k个采样{x1,x2,…,xk},其概率为

p(x1,x2,…,xk)=fD(x1,x2,…,xkθ)

(1)

式中,θ为分布参数.

尽管采样数据来自于分布D,但θ可能未知.一旦获得x1,x2,…,xk,便能从中找到一个关于θ的估计.最大似然估计法是指在所有可能的θ取值中,寻找使该采样可能性最大化的解.

在数学上实现最大似然估计法,首先需要定义最大似然函数为

l(θ)=fD(x1,x2,…,xkθ)

(2)

使该采样可能性最大的θ值即为其最大似然估计.

在NTCP模型参数拟合的应用中,对于患者i,无论采用哪种模型,其NTCP值Ni均可表述为如下的函数形式[8]:

Ni=F(P,di,vi)

(3)

式中,P为模型参数;di为微分后的剂量;vi为体积单元.

对于用来拟合模型参数的一组患者数据,其对数似然函数可表示为

(4)

式中,Ri为参数,如果患者i在临床观察或随访中出现放疗并发症,则Ri=1,否则Ri=0.

利用优化方法将最大似然函数取最大值,便可拟合得到各模型参数.

2 实验

通过对第1节中的最大似然函数进行优化,便可快速准确地得到NTCP模型参数拟合结果.优化方法可以分为两大类:确定性优化方法和随机性优化方法.前者的特点是速度快,但容易陷入局部极小;后者虽然不易陷入局部极小,从概率上可以收敛到全局最优,但是收敛速度比较慢[9].据笔者所知,目前国内外文献未见关于NTCP模型是否为凸函数的讨论,即不确定其是否存在局部最小值.因此,考虑到确定性优化方法在运行速度方面的优势,选择该方法开展实验.

式(4)即为优化的目标函数.考虑到该函数的复杂性,对其是否为凸函数的数学证明也会比较复杂.鉴于此,采用反证法进行讨论.即借助确定性优化方法的特点,从反面证明优化目标函数是否为凸函数.若目标函数为凸函数,即解空间中不存在任何一个点使函数陷入局部最优,则无论取何值为解空间起始点,均能找到一个唯一不变的最优点,该点即为全局最优点;若目标函数为非凸函数,则可能在某一次优化过程中将局部最优点作为返回结果.因此,采用确定性优化方法时,如果在若干次重复的优化过程中得到了不同的解,则表明该目标函数存在局部最小值,即该函数为非凸函数.

在文献[10]的数据基础上,以前列腺癌放疗引起直肠晚期并发症(大于等于二级损伤,LENT/SOMA标准)为例,考察5年随访时间中257例患者出现该并发症的情况.目标函数中的NTCP模型以LKB模型为例[8],某正常器官受照射至出现50%并发症概率所需的剂量T∈[50,100],体积效应因子n∈(0,1),斜率因子m∈(0,1).实验的具体步骤如下:

① 选择确定性优化方法中的单纯形法进行优化.每次优化开始之前,对T,n,m随机取值,作为单纯形优化的起始点.

② 调用Matlab软件运行环境中的fminsearch函数,实现对目标函数的优化.重复运行10次,记录每次优化后得到的解、目标函数值和运行时间.

③ 在相同患者数据基础上,利用模拟退火算法和遗传算法对目标函数分别优化10次,求得全局最优解,并与根据确定性优化方法得到的解进行对比.为保证随机性优化方法能获得全局最优解,将模拟退火算法的初始温度设置为100 ℃,每次降温的衰减系数为0.9,搜索步长为0.1,每一温度下的迭代次数为104;为确保跳出局部极值、找到全局最优解,将遗传算法中的进化代数设置为104.

3 结果与分析

将单纯形算法重复运行10次且每次都随机选取优化起始点,优化结果见表1.由表可知,在第8次和第9次优化过程中,单纯形法于开始阶段便陷入了局部最优解,得到了与其他情况下截然不同的解和最大似然函数值.因此,按照最大似然估计法构成的优化目标函数是非凸函数,存在局部最优解,不适于用确定性优化方法.

表1 单纯形算法的优化结果

当n≈0.02,参数T和m在解空间变化时,最大似然函数取到最小值的解不是唯一的,而是一个区间.当n≈0.02,T≈77.97时,参数m与最大似然函数值的关系见图1.由图1(a)可知,当m=

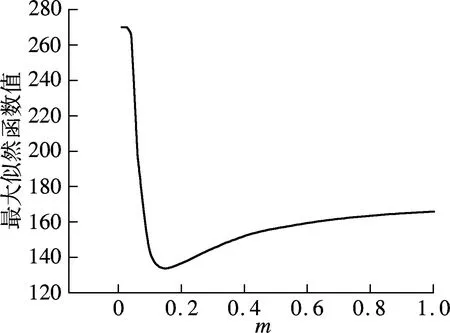
(a) m∈(0,1)

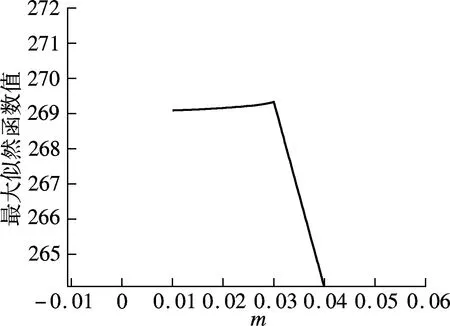
(b) m→0时的局部放大图

0.14时,最大似然函数取得全局最小值,此时的m值即为最大似然函数的全局最优解;当m→0时,曲线存在一个平台,对其放大之后可见一个最大似然函数的局部最小值(见图1(b)),此时的m值即为单纯形算法第8次优化后得到的局部最优解.

综上所述,从优化结果和图形表达2个方面证实了由NTCP模型构成的最大似然函数作为优化目标函数是存在局部最小值的,该目标函数为非凸函数,不适于用确定性优化方法.因此,需要考虑随机性优化方法.选取模拟退火算法和遗传算法,重复运行10次后的优化结果分别见表2和表3.由表可知,模拟退火算法运行时间较长,弱初始值选取不合适,则可能陷入局部最小值,温度无法下降,从而导致优化过程结束;遗传算法的优化结果则更稳定,每次优化后都能找到全局最优解,且每次的运行时间基本相同.因此,在对NTCP建模时,建议使用遗传算法拟合模型参数,确保在最短的时间内获得全局最优解,使所建模型对并发症预测更准确.

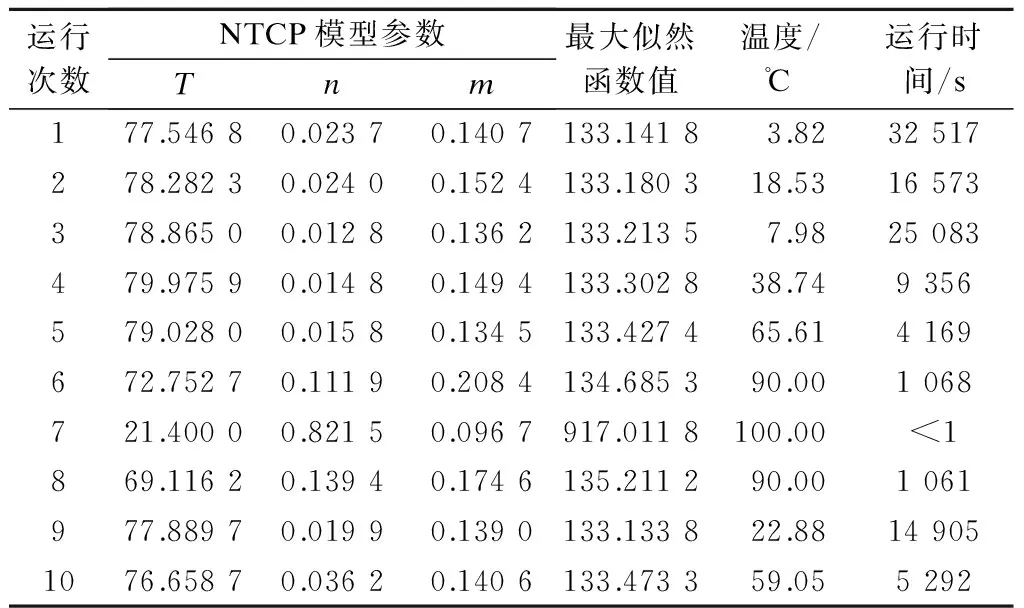
表2 模拟退火算法的优化结果

表3 遗传算法的优化结果

为了证实遗传算法所得的优化结果为全局最优解,可通过全面搜索算法进行验证.在搜索步长足够小的情况下,全面搜索算法可以确保找到全局最优解,但其完成一次全局优化的时间较长.以优化相同样本为例,在运行环境为Intel Core2 Duo CPU,T5670,1.80 GHz,2 GB内存的计算平台上,利用全面搜索算法,计算出最大似然函数值的时间约为0.023 6 s.令T∈[50,100],n∈(0,1),m∈(0,1),取值步长为0.01,则完成全局优化需要进行5×108次计算,大约需要13 d.因此, 全面搜索算法仅适于对其他算法进行验证,不适用于常规的参数优化.

4 结语

本文通过实验方法证明了拟合NTCP模型所构建的最大似然函数是非凸函数,存在局部最优解;对比了不同优化算法在拟合NTCP模型参数方面所表现出的特点.实验结果表明,遗传算法的优化结果和运行时间较稳定,且每次优化结束后都可以给出全局最优解.因此,在对NTCP建模时,建议使用遗传算法拟合模型参数,确保在最短的时间内获得全局最优解,使所建模型对并发症预测更准确.所提方法可以帮助肿瘤放疗工作者在临床随访数据的基础上建立具有群体特异性的放疗并发症预测模型.

References)

[1]Tucker S L, Li M, Xu T, et al. Incorporating single-nucleotide polymorphisms into the Lyman model to improve prediction of radiation pneumonitis[J].IntJRadiatOncolBiolPhys, 2013, 85(1): 251-257.

[2]Strigari L, Pedicini P, D’Andrea M, et al. A new model for predicting acute mucosal toxicity in head-and-neck cancer patients undergoing radiotherapy with altered schedules[J].IntJRadiatOncolBiolPhys, 2012, 83(5): e697-e702.

[3]Gulliford S L, Partridge M, Sydes M R, et al. Parameters for the Lyman Kutcher Burman (LKB) model of normal tissue complication probability (NTCP) for specific rectal complications observed in clinical practise[J].RadiotherapyandOncology, 2012, 102(3): 347-351.

[4]Fellin F, Azzeroni R, Maggio A, et al. Helical tomotherapy and intensity modulated proton therapy in the treatment of dominant intraprostatic lesion: a treament planning comparison[J].RadiotherapyandOncology, 2013, 107(2): 207-212.

[5]Amin N P, Miften M, Thornton D, et al. Effect of induction chemotherapy on estimated risk of radiation pneumonitis in bulky non-small cell lung cancer[J].MedicalDosimetry, 2013, 38(3): 320-326.

[6]de Sanctis V, Bolzan C, D’Arienzo M, et al. Intensity modulated radiotherapy in early stage Hodgkin lymphoma patients: is it better than three dimensional conformal radiotherapy?[J].RadiationOncology, 2012, 7: 129-1-129-9.

[7]Zhu J, Zhang Z C, Li B S, et al. Analysis of acute radiation-induced esophagitis in non-small-cell lung cancer patients using the Lyman NTCP model[J].RadiotherapyandOncology, 2010, 97(3): 449-454.

[8]朱健,李宝生,舒华忠,等.正常组织并发症概率模型综述[J].中国生物医学工程学报,2014,33(2):233-240. Zhu Jian, Li Baosheng, Shu Huazhong, et al. Review of normal tissues complication probability models[J].ChineseJournalofBiomedicalEngineering, 2014, 33(2): 233-240. (in Chinese)

[9]袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,2001:50-51.

[10]Zhu J, Simon A, Ospina J D, et al. Predictive models of bladder toxicity in prostate cancer radiotherapy[J].EurJCancer, 2011, 47(S1): S486.

Parameter fitting method of NTCP predictive model in radiation oncology

Zhu Jian1,2Bai Tong2Li Baosheng1,2Shu Huazhong1Antoine Simon3Renaud de Crevoisier3

(1Laboratory of Image Science and Technique, Southeast University, Nanjing 210096, China)(2Shandong Cancer Hospital and Institute, Jinan 250117, China)(3Laboratoire Traitement du Signal et de l’Image, Université de Rennes 1, Rennes 35510, France)

To establish the population specific NTCP (normal tissue complication probability) prediction model in radiation oncology, a parameter fitting method is proposed. First, the maximum likelihood function is constructed based on the characteristic of the NTCP model. Then, the deterministic optimization method and the stochastic optimization method are used to optimize the maximum likelihood function, respectively. The time cost and the optimization results are analyzed to find the better method for fitting the parameters of the NTCP model. The experimental results show that the maximum likelihood function for fitting the parameters of the NTCP model is non-convex, indicating that there exist the local optimal solutions. The genetic algorithm is the most stable optimization algorithm for fitting the NTCP model, and the running time is less than that of the simulated annealing algorithm. In this algorithm, the global optimal solutions, which are regarded as the parameters of the NTCP model, can be obtained after each optimization. The proposed method can help the researchers in radiation oncology establish the population specific NTCP predictive models based on clinical follow-ups.

tumor; radiotherapy; complication; NTCP (normal tissue complication probability) model

10.3969/j.issn.1001-0505.2015.02.011

2014-10-01. 作者简介: 朱健(1980—)，男，博士，助理研究员；李宝生(联系人)，男，博士，研究员，博士生导师，baoshli@yahoo.com.

国家自然科学基金资助项目(61271312，81272501，81301298)、国家重点基础研究发展计划(973计划)资助项目(2011CB707904).

朱健,白曈,李宝生,等.肿瘤放疗并发症概率预测模型参数拟合方法[J].东南大学学报:自然科学版,2015,45(2):256-259.

10.3969/j.issn.1001-0505.2015.02.011

TP391.9

A

1001-0505(2015)02-0256-04