基于局部特征和集成学习的鲁棒彩色人脸识别算法
2015-04-24邵珠宏欧阳军林舒华忠
邵珠宏 欧阳军林 廖 帆 舒华忠
(东南大学影像科学与技术实验室,南京210096)
基于局部特征和集成学习的鲁棒彩色人脸识别算法
邵珠宏 欧阳军林 廖 帆 舒华忠
(东南大学影像科学与技术实验室,南京210096)
为了充分利用人脸图像的局部信息、改善现有基于整体特征的彩色人脸识别算法的识别率,提出了一种基于局部特征和集成学习分类器的鲁棒彩色人脸识别算法.在特征提取阶段,使用自适应四元数pseudo-Zernike矩(AQPZMs)来描述图像子块的特征.对于具有较大熵的图像子块使用较高阶次的四元数pseudo-Zernike矩(QPZMs)提取特征,反之则使用较低阶次的QPZMs.在匹配识别阶段,使用集成学习分类器进行判别.针对不同彩色人脸图像库的测试结果表明,当人脸图像受到光照、表情等因素影响时,与采用QPZMs或者四元数二维主成分分析(Q2DPCA)进行整体特征提取的识别算法相比,所提算法的识别率更高.
彩色人脸识别;局部特征;四元数pseudo-Zernike矩;集成学习
在计算机视觉和模式识别领域,人脸识别算法引起了广泛关注.一般而言,人脸识别的过程包括特征提取和匹配识别.在灰度人脸识别的问题中,基于主成分分析的识别算法[1-2]备受关注,例如基于向量形式的主成分分析和基于矩阵形式的二维主成分分析、双向主成分分析等.但是,当人脸图像受到表情、光照等因素影响时,使用主成分分析提取特征的识别算法无法获得理想的识别率.实际上,在判断人脸类别的过程中,根据局部信息便能实现匹配.基于此,学者们提出了基于局部特征的人脸识别算法[3-9].根据总体散度矩阵的数量,可将算法大致分为2类:① 基于整体特征的算法,即将人脸图像中不同位置的子块投影到共同的特征空间上,利用所有训练样本的子块来计算平均脸,以得到总体散度矩阵[3, 7];② 基于局部特征的算法,即将人脸图像中每个位置的子块投影到各自的特征空间上,对不同位置的子块分别计算平均脸和总体散度矩阵[4, 8].后者的识别率优于前者.对于单训练样本下灰度人脸表情的识别问题,Kanan等[10]提出了一种采用pseudo-Zernike矩提取局部特征的识别算法.
相对于灰度图像,彩色图像可以提供丰富的视觉感受.随着图像采集设备的不断发展,彩色图像的获取变得容易,彩色人脸识别问题成为近年来计算机视觉领域的研究热点.文献[11-13]表明,与将彩色人脸图像进行灰度化的预处理方法相比,采用四元数矩阵表示的识别算法的识别率更高.但是,这类算法中计算的特征均是针对整幅人脸图像的,算法的鲁棒性较差.为了充分利用人脸图像的局部信息,本文提出了一种基于局部特征的彩色人脸识别算法.
1 局部特征算法描述
1.1 图像表示
对于任意一幅RGB彩色图像f(x,y),将3个颜色通道分量作为四元数的虚部,则
f′(x,y)=ifR(x,y)+jfG(x,y)+kfB(x,y)
(1)
式中,fR(x,y),fG(x,y),fB(x,y)分别表示彩色图像的红、绿、蓝分量.
1.2 特征提取
考虑到人脸图像不同区域的识别能力不同,结合人脸图像子块的平均熵,提出了一种基于自适应四元数pseudo-Zernike矩(AQPZMs)的局部特征表示方法.如果某个图像子块具有较大的熵,则使用较高阶次的四元数pseudo-Zernike矩(QPZMs)描述其特征;反之,则使用较低阶次的QPZMs.
1.2.1 彩色图像的熵
对于一幅离散化的灰度图像,熵定义为
(2)
式中,pi表示第i个灰度级出现的概率;s表示灰度级的数目,此处取s=256.
RGB彩色图像由红、绿、蓝3个颜色分量构成,那么RGB彩色图像的熵H′可定义为颜色通道分量图像熵的平均值,即
(3)
式中,HR,HG,HB分别表示红、绿、蓝颜色分量的熵.
1.2.2 局部QPZMs
对于图像子块fp, q(a,b),阶次为n、重复度为m的四元数pseudo-Zernike矩[13]为
式中
Rn,m(r)=
(5)

1.2.3 局部特征提取
使用QPZMs提取人脸图像子块特征时,需建立图像子块平均熵与QPZMs阶次之间的关系.
首先,根据训练样本中的部分或者全部人脸图像,计算得到平均人脸图像.然后,根据平均人脸图像熵,得到与图像具有相同尺寸的熵图像E(x,y),其计算式为
E(x,y)=H′(FS(x,y))
(6)
式中,FS(x,y)表示经过(x,y)处像素点的窗口.
基于不同邻域尺寸得到的归一化熵图像见图1.图中,S为邻域尺寸.

(a)原图像

(b) S=3×3像素

(c) S=5×5像素
(d) S=7×7像素
(e) S=9×9像素
图1 归一化熵图像
将归一化熵图像分块,(p,q)处图像子块的平均熵为
W2(q-1)+yb)
(7)
描述图像子块的特征时,根据子块平均熵的大小,使用不同阶次的QPZMs提取特征,其流程图见图2.

图2 局部特征提取流程图
2 分类器选择
2.1 最近邻分类器
在匹配识别阶段,人脸图像识别算法主要采用基于欧式距离的最近邻分类器.对于2个维度均为n1的四元数特征向量v1,v2,其间距为
(8)
对于待识别的人脸图像,分别计算其特征向量与所有训练样本特征向量之间的距离,将最小距离所对应的训练样本类别作为待测样本类别.
2.2 集成学习分类器
假设图像划分的子块数量为Nb,将每个子块作为单独的分类器,则共计Nb个分类器.对于类别总数为L的识别问题,每个分类器生成L个置信度.
令Cl,k表示第k个图像子块属于类别l的置信度,即
(9)
式中,α为归一化系数;σ为Dl,k对置信度的影响参数;Dl,k为图像子块特征vk与类别l中样本特征vc之间的最小F-范数距离,即
Dl,k=min(‖vk-vc‖F)
(10)
对一幅图像中所有子块的置信度求和,从而得到待识别样本属于每个类别的总体置信度Cl,即
(11)
将最大总体置信度所属的类别作为待测样本的类别.当存在多个最大总体置信度时,可以将其随机地归类于最大置信度所属的类别.
3 实验结果
为了验证所提算法的性能,选择不同的彩色人脸图像库进行实验.实验中所选用的Aberdeen人脸图像库[14]共计377幅图像,包括29个不同类别,每个类别包含13幅不同光照、表情下的正面图像,部分图像见图3(a).所选用的GT人脸图像库[15]中共计750幅图像,包括50个人,每个人包含15幅不同光照、表情下的正面图像,部分图像见图3(b).

(a) Aberdeen

(b) GT
根据眼睛的位置对人脸图像进行裁剪,将其尺寸调整为160×128像素.对于2个图像库,均选取前10幅图像作为训练集,其余图像作为测试集.对人脸图像按照W1×W2=160×64,80×128,80×64,53×128,53×64,53×42,40×128,40×64,40×42,40×32像素进行分块.实验中集成学习分类器参数σ的取值范围为1~100.
3.1 基于AQPZMs的彩色人脸识别
使用AQPZMs提取人脸图像子块的特征时,需要考虑以下2个因素:① 熵图像邻域的尺寸;② 图像子块的平均熵与QPZMs阶次之间的关系.计算归一化熵图像时,首先根据训练样本中每个类别的第1幅人脸图像,得到平均人脸图像,再根据彩色图像熵的定义,采用不同的邻域尺寸得到归一化熵图像.对于Aberdeen人脸图像库的熵图像(S=5×5像素),不同分块时的子块平均熵见图4.图中,区域颜色越深表示子块的平均熵数值越小.

(a) W1×W2=160×64像素

(b) W1×W2=80×128像素

(c) W1×W2=80×64像素

(d) W1×W2=53×128像素

(e) W1×W2=53×64像素
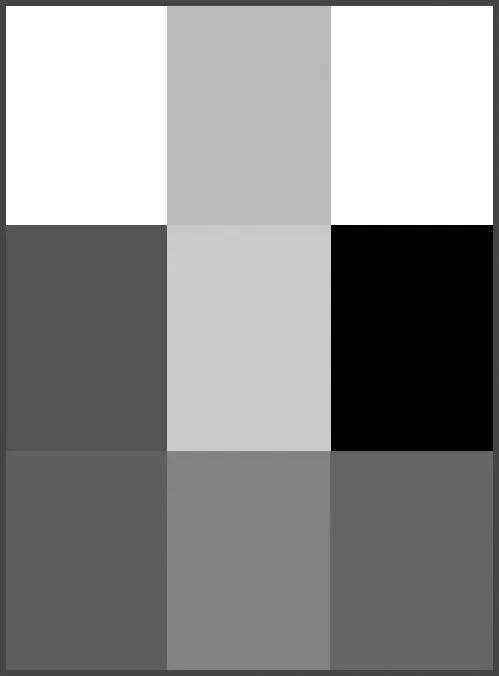
(f) W1×W2=53×42像素

(g) W1×W2=40×128像素

(h) W1×W2=40×64像素

(i) W1×W2=40×42像素

(j) W1×W2=40×32像素
结合采用QPZMs提取整体特征进行识别时阶次对识别率的影响和对人脸图像进行不同分块时子块平均熵的变化情况,根据实验中平均熵与QPZMs阶次的关系(见表1),提取人脸图像子块的特征.首先,利用最近邻分类器,采用AQPZMs提取特征,对不同邻域尺寸、分块时的识别率进行统计,结果见表2.由表可知,当图像分块固定时,随邻域尺寸变化,识别率变化较平稳.GT人脸图像库上的结果与此类似.
利用集成学习分类器进行判别,得到参数σ变化时2个图像库的识别率(见图5).由图可知,对于Aberdeen人脸图像库,最高识别率为94.25%;对于GT人脸图像库,最高识别率为89.60%.

表1 熵与QPZMs阶次的关系
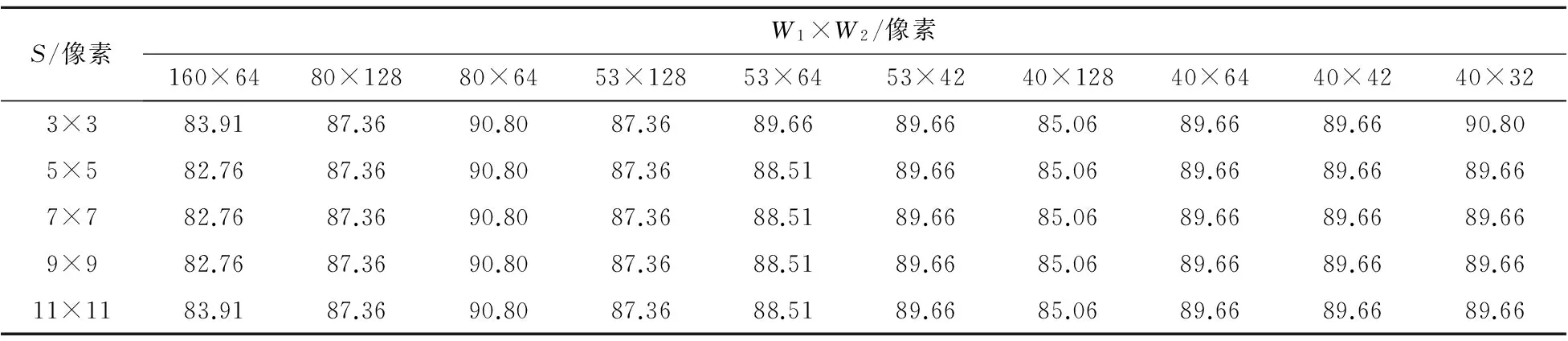
表2 Aberdeen人脸图像库的识别率 %

图5 σ变化时2个图像库的识别率(S=5×5像素)
3.2 算法比较
为进一步评估采用局部特征和集成学习分类器进行人脸识别的优势,考察了基于不同特征、选用不同分类器所得的最高识别率,结果见表3.由表可知,与使用QPZMs,Q2DPCA提取整体特征的识别算法相比,采用AQPZMs进行局部特征提取的识别算法的识别率更高.当人脸图像未分块时,使用2种分类器得到的识别率一致;但在分块情况下,使用集成学习分类器可以进一步提高识别率.

表3 不同识别算法的最高识别率比较 %
4 结语
针对不同光照、表情等复杂条件下的彩色人脸识别问题,提出了一种基于局部特征和集成学习分类器的鲁棒识别算法.首先,根据熵图像的平均区域熵,使用不同阶次的QPZMs提取人脸图像子块的特征;然后,利用集成学习分类器进行匹配识别.实验结果表明,与采用QPZMs或者Q2DPCA进行整体特征提取的识别算法相比,所提算法的识别率更高.下一步的研究工作将考虑使用加权的局部特征进行识别.
References)
[1]Yang J, Zhang D, Frangi A F, et al. Two-dimensional PCA: a new approach to appearance-based face representation and recognition [J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 2004, 26(1): 131-137.
[2]Zuo W M, Zhang D, Wang K Q. Bidirectional PCA with assembled matrix distance metric for image recognition [J].IEEETransactionsonSystems,ManandCybernetics:PartB:Cybernetics, 2006, 36(4): 863-872.
[3]Gottumukkal R, Asari V K. An improved face recognition technique based on modular PCA approach [J].PatternRecognitionLetters, 2004, 25(4): 429-436.
[4]Hsieh P C, Tung P C. A novel hybrid approach based on sub-pattern technique and whitened PCA for face recognition [J].PatternRecognition, 2009, 42(5): 978-984.
[5]Eftekhari A, Forouzanfar M, Abrishami M H, et al. Block-wise 2D kernel PCA/LDA for face recognition [J].InformationProcessingLetters, 2010, 110(17): 761-766.
[6]Wang H X. Block principal component analysis with L1-norm for image analysis [J].PatternRecognitionLetters, 2012, 33(5): 537-542.
[7]Cavalcanti G D C, Ren T I, Pereira J F. Weighted modular image principal component analysis for face recognition [J].ExpertSystemswithApplications, 2013, 40(12): 4971-4977.
[8]Mashhoori A, Jahromi M Z. Block-wise two-directional 2DPCA with ensemble learning for face recognition [J].Neurocomputing, 2013, 108: 111-117.
[9]Yan L, Pan J S, Chu S C, et al. Adaptively weighted sub-directional two-dimensional linear discriminant analysis for face recognition [J].FutureGenerationComputerSystems, 2012, 28(1): 232-235.
[10]Kanan H R, Faez K, Gao Y. Face recognition using adaptively weighted patch PZM array from a single exemplar image per person [J].PatternRecognition, 2008, 41(12): 3799-3812.
[11]Sun Y, Chen S, Yin B. Color face recognition based on quaternion matrix representation [J].PatternRecognitionLetters, 2011, 32(4): 597-605.
[12]Xu Y. Quaternion-based discriminant analysis method for color face recognition [J].PloSONE, 2012, 7(8): e43493-1-e43493-4.
[13]陈北京, 孙星明, 王定成, 等. 基于彩色图像四元数表示的彩色人脸识别[J]. 自动化学报, 2012, 38(11): 1815-1823. Chen Beijing, Sun Xingming, Wang Dingcheng, et al. Color face recognition using quaternion representation of color image [J].ActaAutomaticaSinica, 2012, 38(11): 1815-1823. (in Chinese)
[14]2D face sets[EB/OL].[2014-08-25]. http://pics.stir.ac.uk/2D_face_sets.htm.
[15]Nefian A V. GT face database [EB/OL]. [2014-08-25]. http://www.anefian.com/research/face_reco.htm.
Robust color face recognition algorithm based on local features and ensemble learning
Shao Zhuhong Ouyang Junlin Liao Fan Shu Huazhong
(Laboratory of Image Sciences and Technology, Southeast University, Nanjing 210096, China)
To make full use of local information of face images and improve the recognition rate of the existing color face recognition algorithm based on global features, a robust color face recognition algorithm based on local features and ensemble learning classifier is proposed. In the feature extraction stage, the adaptive quaternion pseudo-Zernike moments (AQPZMs) are used to describe the features of image blocks. The features of image blocks with larger entropy are described by quaternion pseudo-Zernike moments (QPZMs) with higher order. On the contrary, the QPZMs with lower order are used to describe the features of image blocks with smaller entropy. In the classification stage, the ensemble learning classifier is used for identification. The experimental results of different color face datasets show that compared with the recognition algorithms exploiting QPZMs or quaternion two-dimensional principal component analysis (Q2DPCA) to extract global features, the proposed algorithm can achieve higher accuracy when the face images are affected by the factors such as illumination, facial expression and so on.
color face recognition;local feature;quaternion pseudo-Zernike moment;ensemble learning
10.3969/j.issn.1001-0505.2015.02.010
2014-10-15. 作者简介: 邵珠宏(1986—),男,博士生;舒华忠(联系人),男,博士,教授,博士生导师,shu.list@seu.edu.cn.
国家重点基础研究发展计划(973计划)资助项目(2011CB707904)、国家自然科学基金资助项目(61073138,6110314,61201344,61271312).
邵珠宏, 欧阳军林,廖帆,等.基于局部特征和集成学习的鲁棒彩色人脸识别算法[J].东南大学学报:自然科学版,2015,45(2):251-255.
10.3969/j.issn.1001-0505.2015.02.010
TP391
A
1001-0505(2015)02-0251-05
