云环境下聚类分解的高维数据混合索引方法

王 倩,朱 变

大数据是云计算的基础和核心技术.随着以博客、微博等新型的社交网络的逐渐呈现,以及物联网等技术的兴起,大数据时代已经到来.2008年,Nature推出Big Data专刊[1-5].2011年,Science推出Dealing with Data专刊[6],主要是关于大数据相关的问题进行讨论.关于大数据的定义没有统一的概念.大数据的概念比较有代表性的是3V定义[7].还有关于4V的定义,就是在3V的基础上增加了新的特性.4V的第4个V给出的定义也不统一,国际数据公司认为第4个V是大数据具有价值性,而IBM认为第4个V应该具有真实性[8].

大数据的产生先后经历了3个阶段.第一阶段是运营式阶段,这个阶段是数据量的第一次大的飞跃,比如:超市的销售记录系统、银行的交易记录系统、医院病人的医疗记录等等,这一阶段数据的产生方式是被动的.第二阶段是用户原创内容阶段,这个阶段是数据量出现的第二次大的飞跃,但是真正数据量产生是在Web2.0时代.第三阶段是感知式系统阶段,这个阶段是大数据产生最根本的原因.随着技术的不断发展,人们有能力制造带有处理功能的传感器,遍布于社会各个角落,不断地产生新的数据.这一阶段数据的产生方式是自动的.面对庞大的数据资源,如何有效地存储和高效地查询这些大数据是当前要解决的问题.

大数据的数据类型包括非结构化的、半结构化的和结构化的数据.按照它的应用类型分为三类,海量交易数据、海量交互数据和海量处理数据.企业OLTP(联机事务处理)应用属于海量交易数据类.比如:关系数据库的增、删、改和查.传感器、GPS和Web信息等属于海量交互数据类.企业OLAP应用(联机分析处理)属于海量处理数据类,是数据仓库的核心部分.

图像、生物信息等领域需要对大数据集进行相似性的查询.大量数据将引起较高的查询代价,所以利用各种索引结构管理特征向量.索引结构分两种结构.第一种是基于顺序扫描的索引,它是通过扫描来进行估计文件,比如:VA-File.在国内,索引结构也有相关的研究,比如:基于矢量的量化索引方法[9]、基于聚类分解的高维度量空间索引[10]等.第二种是树状索引的结构,比如,R-Tree,MTree等.

在高维空间中,如果维数远超过10维时,数据集的聚集情况变差,树状索引效率随之下降.如果维数小于10维时,数据的聚集强,已知的树状索引结构已经证明了它的有效性.那么,如何解决中等规模维数的数据(大于10维而小于610维)成为一个复杂的问题.

对此,笔者提出了云环境下聚类分解的高维数据混合索引方法.首先,通过聚类的分解来分割数据,减少查询的数据访问;然后,分两个阶段进行单节点的最近邻计算:第一阶段,以叶节点为单位,通过扫描线算法来获取节点内部所有对象的局部最近邻结果;第二阶段,依据计算的结果得出启发式的裁剪距离,并采用范围查询算法获取外部的最近邻对象.

1 相关工作

高维数据的索引分为两类.第一类是向量空间的索引,采用类B+-tree的索引结构而进行的索引[11],比如:R树.这种索引的不足是在计算距离的费用昂贵.第二类是度量空间的索引,可以弥补第一类索引存在的不足.这类索引首先要选取距离的参考点,依据数据对象和各参考点计算距离.然后索引数据的对象,比如:M-tree[12].但这种索引对树节点的利用率较低,影响了M-tree的查询效率.

无论采用树状索引结构还是采用顺序索引结构都是属于单一的索引策略,没有考虑到数据的分布和索引策略之间的关系.有些学者将树状索引结构和顺序索引结构结合在一起进行研究,依据数据分布情况选择适当索引的策略,并进行分类:第一类是基于顺序索引方法采用树状的索引结构[13],不需要扫描所有的压缩文件.另一类是引入顺序扫描方法到树状的索引里,比如:2004年,Edgar[14]采用顺序扫描的方法对一部分的数据顺序扫描,研究结果表明在高维的承受力上得到了提高.2006年,在高维度量空间索引上,张军旗等人[10]提出了一种聚类分解的方法,理论证明,该方法是最优的分割方法.

2 高维数据混合索引

首先,采用Kmeans聚类算法对数据集进行更细致地划分,并根据最佳聚类分解数目进行聚类分解.然后,计算单节点的最近邻结果,此计算分两个阶段:第一个阶段,以叶节点为单位,通过扫描线算法来获取节点内部所有对象的局部最近邻结果;第二个阶段,依据计算的结果得出启发式的裁剪距离,并采用范围查询算法获取外部的最近邻对象.

2.1 数据划分

首先,采用Kmeans聚类算法[15],该算法是MacQueen在1967年提出,具体流程如下:

(1)选择样本点k个,这k个样本点是从样本数据集D里选择出来的,再将选择出的样本点值作初始聚类中心的值;

(2)当第j次迭代时,依次计算样本点D中的所有点ptt(=1,…,n)到各个簇中心ui(j)的欧式距离d t(,i);

(3)根据第2步计算结果找到最小的距离,把最小距离的pt划入ui(j)距离的最小簇;

(4)对每个簇的聚类中心进行更新;

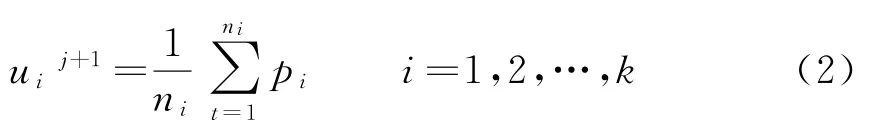
(5)对数据集D中的所有样本点进行平方误差Ei的计算,得出的结果再与前一次Ei-1误差进行比较.

然后,采用聚类分解的方法,对数据进行更细致地划分.高维空间聚类数据处的位置是稀疏的,聚类之间的重叠现象比较严重,所以,在查询效率上大多数的聚类是不高的.分割数据后建立树状索引.

采用聚类分解方法对数据点进行平均分解:

在各个聚类环中数据点数是相同的.当数据间的距离接近于类似钟形的分布时,聚类环内外半径差较大是分布稀疏的数据,而半径差较小是分布密集的数据.如果数据距离的分布是接近于均匀的,那么,分解方法采用等同平均分解聚类的半径.

设聚类内的数据点数用 cluster 表示,各个聚类需分解的聚类环数用m表示,cluster/m为被分解的各个聚类环内部的数据点的个数,r 1,r 2是表示环的内半径和外半径,按聚类中数据点的数量进行平均分解的步骤:

第一步 按照升序排列,各个数据点和聚类中心之间的距离,并形成一个队列Q;

第二步 设内半径ri1=0是第一个聚类环,第cluster /m个点与聚类中心之间的距离也就是第一个聚类环的外半径ro1;

第三步 设第i个聚类环的内半径rii=roi-1,在队列Q中第i个聚类环的外半径roi就是第i× (cluster/m)个点和聚类中心之间的距离;

第四步 重复前三步操作,分出第m个聚类环停止操作.

2.2 单节点最近邻计算

首先,建立Hilbert小顶锥,让根节点入堆、依次排序来取Hilbert值最小的的节点.假如这个节点是内部的节点,那么该节点所有子节点入堆;如果该节点不是内部节点而是叶节点,那么内部对象的最近邻就计算出来.如果堆是空的话,那么完成了全局最近邻的计算.

要计算叶节点ζ内部对象的最近邻,可以分为两个阶段来完成:第一个阶段,计算叶节点ζ内部最近邻和临近矩阵Mvζ;第二个阶段,Mvζ作为查询的窗口,利用范围的查询得到可能影响最近邻结果的外部对象,并计算完备性的结果.

对于第二个阶段出现问题,做了这样的处理:

(1)如果叶节点ζ不与内部任一对象的临近圆相交,则丢弃.

(2)如果叶节点ζ与内部任一对象的临近圆相交,更新相应对象的最近邻结果;如果出现多于两个或两个以上的对象存在的话,则采用首次获得的对象.

3 实验比对

为了验证所提出的方法具有良好的查询效率和性能,笔者从两个方面进行了实验比对:(1)与单纯的聚类法,查询效率比较;(2)与其他相关索引,性能比对.

为了保证实验的正确性,实验中用到的数据集从http://dbgroup.cs.tsinghua.edu.cn/liyan/u_mining.tar.gz下载.实验所使用硬件系统为2.8 GHz CPU,1G内存的计算机.根据查询代价最小化的聚类数目得出,对本数据集最优的聚类分解总数为2 268(根据公式3得出,文献[10]中已得到证明).

3.1 查询效率的对比

与单纯的聚类方法相比,随着数量的增加,基于聚类分解方法响应时间越来越快.实验结果表明,笔者提出的方法具有良好的查询效率.聚类数据分布稀疏,聚类间相互重叠的情况严重,大量的聚类参与查询导致查询效率不高.采用聚类分解方法,对分割数据建立树状索引,在查询上有效地避免聚类边缘相交引起的对整个聚类搜索,从而提高了查询效率,如图1所示.

3.2 性能比对

本组实验选择有代表性的索引方法:M-tree、顺序查找、iDisance进行性能方面的实验分析.图2所示,M-tree响应时间最慢,顺序查找和iDisance在响应时间上是相当的,而云环境下聚类分解的高维数据混合索引方法明显高于M-tree、顺序查找和iDisance方法的效率.

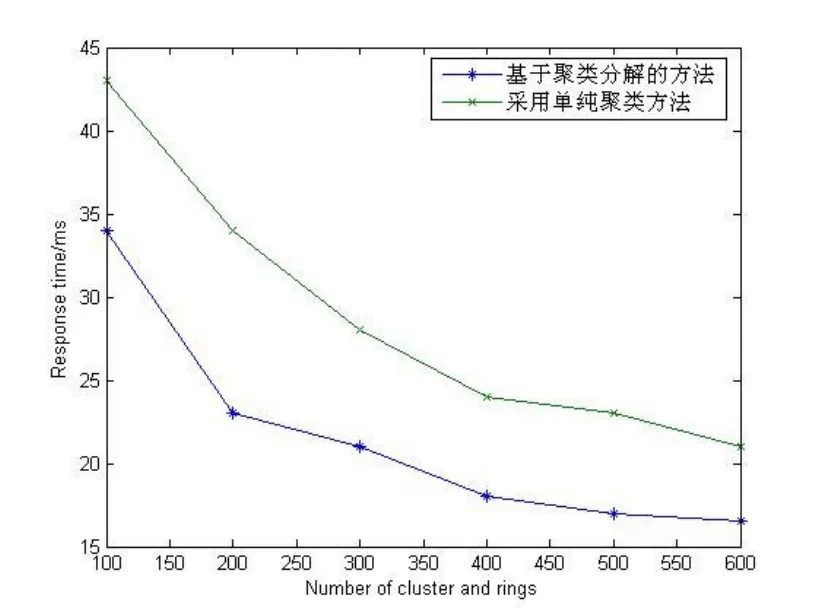
图1 聚类分解与单纯的聚类方法的查询效率对比

图2 与其他方法在性能上的比较

4 结束语

笔者提出了一种基于云环境下聚类分解的高维数据混合索引方法.第一步,采用Kmeans聚类算法对数据进行更细致地划分;第二步,计算单节点的最近邻.这一步分为两个阶段完成.实验分析表明,与单纯的聚类方法相比,笔者提出的方法具有良好的查询效率.与M-tree、顺序查找、iDisance相比,基于聚类分解的混合索引方法在复杂查询模式下具有良好的负载均衡.

参考文献:

[1]FOSTER I,YONG ZHAO,RAICUI,et al.Cloud computing and grid computing 360-degree compared[C]//Proceedings of the 2008 Grid Computing Environments Workshop.Washington,DC:IEEE Computer Society,2008:1-10.

[2]ARMBRUSTM,Fox A,GRIFFITH R,et al.Above the clouds:A Berkeley view of cloud computing[EB/OL].http://www.eecs.berleley.edu/Pubs/Techrpts/2009/EECS-2009-28.pdf.2009.

[3]陈康,郑伟民.云计算:系统实例与研究现状[J].软件学报,2009,20(5):1337-1348.

[4]冯登国,张敏,张妍,等.云计算安全研究[J].软件学报,2011,22(1):71-83.

[5]Nature.Big Data[EB/OL].http://www.nature.com/news/specials/bigdata/index.html.2012.

[6]Science.Special online collection:Dealing with data[EB/OL].http://www.sciencemag.org/site/special/-data/,2011.

[7]Grobelnik M.Bigdata computing:Creating revolutionary breakthroughs in commerce,science,and society[R/OL].http://videolectures.net/eswc-2012_grobelnik_big_data/.2012.

[8]Big data[EB/OL].http://en.wikipe-dia.org/wiki/big_data.2012.

[9]Ye HJ,Xu GY.Fast image search using vectorquantization[J].Journal of Software,2004,15(9):1361-1374.

[10]Zhang JQ,Zhou XD,Wang M,Shi BL.Cluster splitting basted high dimensionalmetric space index B+-Tree[J].Journal of saftware,2008,19(6):14011412.

[11]Guttman A.R-trees:A dynamic index structure for spatial searching.In:Youmark B,ed.Pro.of the ACM Int’1 Conf.On Management of Data.Boston:ACM Press,1984:47-57.

[12]Ciaccia P,Patella M,Zezula P.A cost model for similarity queries in metric spaces.In:Proc.of the 17thACM conf.on Principles on Database Systems.New York:ACM Press,1998:59-68.

[13]Berchtold S,Bohm C,Jagadish HV,et al.Independent quantization:An index compression technique for highdimensional data spaces.In:Proc.Of the 16th Int’1 Conf.on data Engineering(ICDE 2000).New Orleans:IEEE Computer Science Society Press,2000:577-588.

[14]Chavez E,Herrera N,Reyes N.Spatial approximation+se-quential scan=efficient metric indexing.In:Proc.Of the XXIV Int’1 conf.Of the Chilean(SCCC 2004).Computer Science Society,2004:121-128.

[15]MacQueen J.In:Proc.Fifth Berkeley Symp.On Math.Statist.And Prob.,Univ.of Calif.Press,1976.