基于ABAQUS的管节点应力集中系数研究

李世铭， 谭 越， 王春升

(中海油研究总院， 北京 100027)



基于ABAQUS的管节点应力集中系数研究

李世铭， 谭 越， 王春升

(中海油研究总院， 北京 100027)

该文基于Abaqus/Standard程序，计算得出了有限元热点应力修正系数。在此基础之上分析了K型管节点热点应力沿相贯线区域变化趋势，讨论了单元类型对于热点应力计算结果的影响以及有限元方法与SACS程序EFT经典理论的区别，分析了空间管节点不同平面杆件之间对于应力集中系数计算结果的影响。

ABAQUS；应力集中系数；热点应力；疲劳设计

0 引言

在固定式导管架平台设计过程中，疲劳寿命一般采用S-N曲线来描述，其中S代表了节点中沿焊缝周围最大的应力幅值，而应力集中系数(SCF)直接决定了实际应力循环幅值[1,2]。因此，将管节点应力集中现象的分析结果作为海洋平台管节点疲劳寿命估算的依据，以解决管节点的安全问题，是目前海洋平台设计需要解决的重要课题之一[2]。

目前，就导管架平台疲劳评估中应力集中系数的计算，工程设计人员普遍采用SACS软件中的Elthymiou公式[3]。该方法根据大量有限元计算结果拟合得出了适用于T型、Y型以及K型等简单搭接关节点的方程组。然而，对于由多个简单管节点焊接而成的复杂管节点的计算，SACS程序的做法是将其拆分为几个简单管节点分别计算SCF值之后再进行疲劳评估。因此，该文基于Abaqus/Standard程序，求解管节点应力集中系数，以探讨复杂管节点中不同平面的简单管节点之间对于SCF值的相互影响，为管节点疲劳设计提供参考。

1 有效性验证

1.1 验证模型

计算方法有效性验证是后续工作的前提，该文参考DNV-RP-C203疲劳设计规范[4]中的试件1和试件2进行分析，试件几何模型如图1所示。

图1 试件几何模型

1.2 热点应力计算及单元选取

表1 不同单元类型试件热点应力计算结果

由计算结果可知，目标值与计算值的误差基本控制在了15%以内，具备了较高的工程精度。而且采用Abaqus/Standard计算得到的值都大于目标值，后续的热点应力计算结果将乘以f以做修正。

2 K型管节点应力集中系数数值分析

2.1 几何模型

该文采用的K型管节点的几何参数如图2所示，具体尺寸见表2。

图2 K型管节点的几何参数符号

表2 K型管节点尺寸

2.2 载荷施加与边界设置

采用API RP 2A中的加载方式以方便与SACS中EFT公式计算值进行对比，如图3所示。

图3 边界及载荷条件

2.3 计算结果分析

分别采用壳元(CPS8)与固体元(C3D20)进行热点应力计算，计算结果考虑修正系数。该文仅以面内弯矩加载时的情况来分析有限元计算结果与SACS程序EFT公式的结果进行对比，计算结果如图4、图5所示。图5中Φ为沿焊缝一周的角度，零点位于Crown Heel冠踵。

图4 面内弯矩加载时K型管节点计算结果

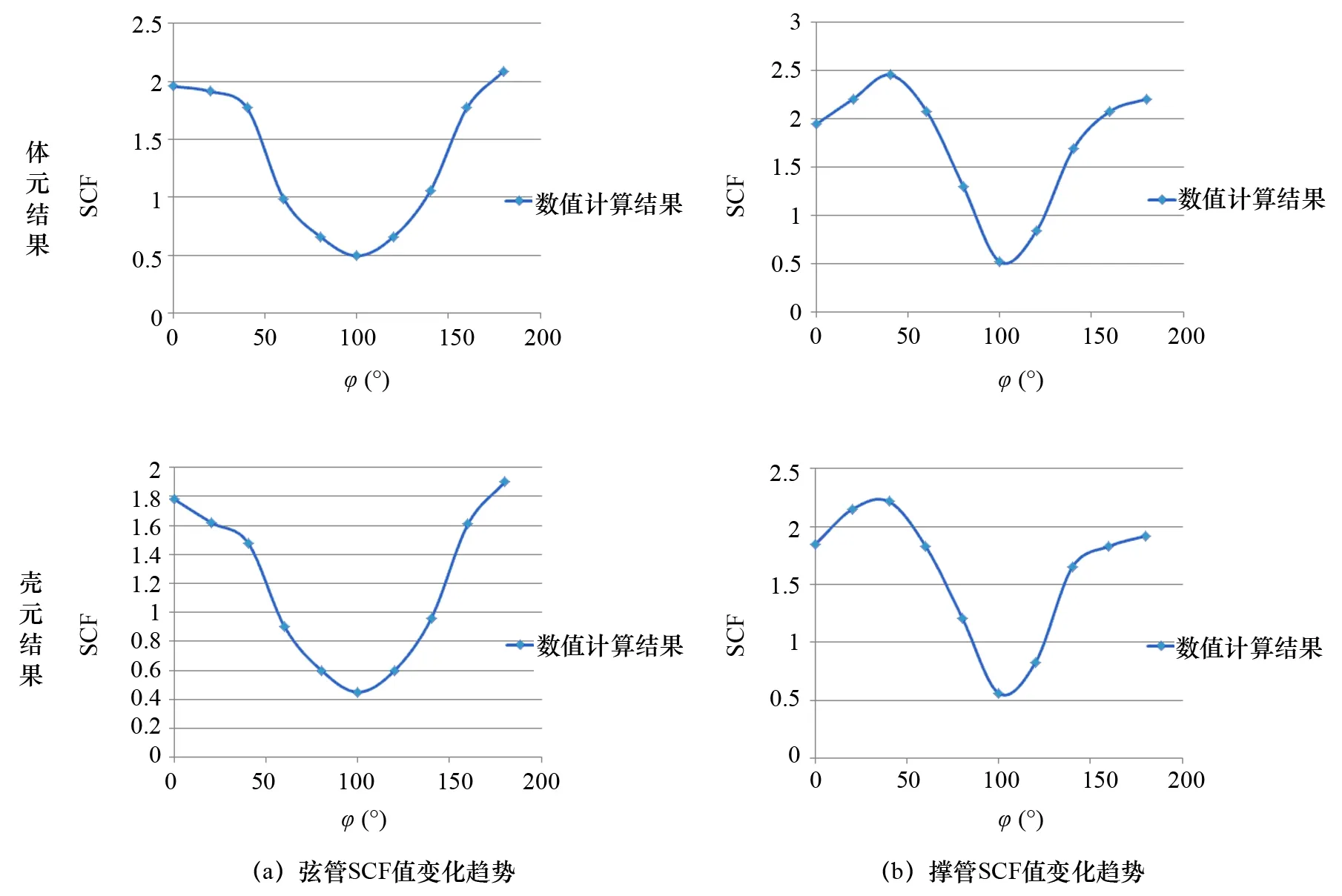
图5 面内弯矩加载时弦管与撑管SCF值沿焊缝变化趋势

由计算结果可以看出，对于弦管与撑管SCF值沿焊缝变化趋势，壳元模型与三体元模型计算结果变化趋势基本一致。表3列出了不同单元类型受平面内弯矩作用时撑杆和弦杆的SCF值与EFT计算值的比较结果。

表3 受平面内弯矩作用时撑杆和弦杆的SCF值比较

结合图4、图5和表3可以看出，与EFT经典理论计算结果不同，由数值计算方法得出的热点应力并非位于冠部跟点，而是在与跟点夹角30°左右的位置。这与API RP 2A规范[4]描述一致，也在一定程度上证实了该文数值模拟的准确性。另外，壳单元模型应力集中系数结果较实体单元模型小，这是由于壳单元并不能模拟出管节点相贯线撑杆与弦管壁厚方向的应力变化，即忽略了壁厚的影响。可见实体单元能够更真实地描述管节点相贯线附近的应力集中现象。

然而，计算效率对于海工设计是一个不可忽视的因素。建立实体单元模型的最大缺点就是网格划分慢，有时可能需要专门的网格划分软件,如Hypermesh、Femap等来提高网格质量，此举不可避免地降低了设计效率。所以面对设计效率与计算精度这一矛盾，采用8节点厚壳单元来提高效率也是可以的。

3 空间管节点应力集中系数数值分析

SACS程序中EFT理论主要针对简单管节点进行计算，即所有杆件都在一个平面或者平面间的角度不超过15°。例如，对于如图6所示的空间管节点，SACS程序的EFT理论的具体做法是将其拆分成如图7(a)和图7(b)所示的K型节点和T型节点，分别计算其SCF值，再利用S-N曲线校核其寿命。为探究管节点不同平面杆件的影响，针对图6、图7所示模型进行述职计算，其中参照API RP 2A中K、T型简单管节点进行加载以及边界条件的设置。SACS程序以及有限元计算结果分别见表4、表5。为了方便比较，将图6、图7(a)与图7(b)所示模型分别命名为模型1、模型2和模型3。

图6 空间管节点模型(模型1)

图7 空间管节点拆分结果

表4 SACS程序计算结果

节点类型杆件直径(cm)厚度(cm)AX CRAX SDIN PLOU PLK型撑杆61．01．32．52．52．685．76弦杆76．22．23．493．492．247．74T型撑杆61．01．32．467．252．637．09弦杆76．22．24．088．482．729．51

表5 空间管节点应力集中系数计算结果

其中：AX-CR表示轴向加载时冠点位置；AX-SD表示轴向加载时鞍点位置；IN-PL表示面内弯矩加载；OU-PL表示面外弯矩加载。

由表4、表5计算结果可知，对于图6所示的YZ平面的K型节点，XZ平面的T型撑杆将使其SCF值略增大；而反过来，YZ平面的K型节点的存在将大大减小XZ平面T型节点在各种加载模式下的SCF值。不同平面之间杆件的存在将影响其他平面杆件的应力集中系数计算结果。而SACS程序中并没有考虑平面外不同类型节点之间的相互影响，由此也将影响到疲劳寿命的评估。

4 结论

该文基于Abaqus/Standard模块，参照最新DNV疲劳规范验证了计算方法的有效性，并对简单K型管节点与空间管节点进行应力集中系数的计算，得到如下结论：

(1) 采用该文计算方法，DNV疲劳设计规范中的热点应力计算值与目标值的误差基本控制在了15%以内，而且无论是壳单元还是实体单元，计算值都大于目标值，即有限元热点应力计算皆小于1。

(2) 选用壳单元建模，计算时在减小储存空间、缩短运算时间的基础上保证了一定的精度。但其采用中面轴线建模的方式将无法真实反映关键内外表面的应力。实体单元能够更真实的描述管节点相贯线附近的应力集中现象，但是网格划分的困难将导致设计效率降低。

(3) 相较于SACS程序中的EFT理论，采用有限元建模计算的方式能够更加准确的找到热点应力位置与大小。SCF经典公式只针对简单管节点而无法计算真实的、复杂的空间节点形式，而实际上，不同平面之间杆件的存在将影响其他平面杆件的应力集中系数计算结果。因此，复杂空间节点的详细数值建模很有必要。

[1] Peter W M. Design of Welded Tubular Connections-Basis and use of AWS Code Provisions[R]. Civil Engineering Consultant, Shell Oil Company, Houston, Texas, U.S.A. 1992.

[2] 杨铮,金伟良. Y型管节点应力集中系数有限元分析[J]. 中国海洋平台，2004，19(4)：17-21.

[3] 姜萌. 近海工程结构物—导管架平台[M]. 大连：大连理工大学出版社，2005.

[4] API RP 2A. Recommended Practice for Planning, Designing, and Constructing Fixed Offshore Platforms-Working Stress Design[S].2000.

[5] DNV-RP-C203.Fatigue strength analysis of offshore steel structures[S]. 2010.

Research on Stress Concentration FactorBased on ABAQUS

LI Shi-ming， TAN Yue， WANG Chun-sheng

(CNOOC Research Institute, Beijing 100027, China)

The paper obtained the hot spot stress correction factor by referring to DNV RP-C203. On These Foundations, variation tendency of k joints intersecting line area is analyzed; the influence of element type on calculated result of FE hot spot stress and the difference between FE method and Efthymiouequation are discussed; the influence of non-coplanar member on SCF is calculated.

ABAQUS; SCF; hot spot stress; fatigue design

2014-11-06

国家科技重大专项 “南海深水油气开发示范工程”(2011ZX05056)。

李世铭(1987-)，男，工程师。

1001-4500(2015)03-0095-06

P75

A