金融投资_参考网

金融投资

2015-04-24佘文翀

科技视界 2015年30期

宗晨佘文翀徐元

（河海大学，江苏南京210098）

对于要求一，我们建立了正态分布模型（模型一）和蒙特卡罗模拟模型（模型二）。对于模型一，用正态分布法进行分析；对于模型二，我们用蒙特卡罗法进行分析。

对于要求二，我们由正态分布的可加性知：Z=X1+X2～N(14.9726,194.1238),再用要求一的解法，求得下一个周期内的损失的数额超过10万元的可能性为3.65%，以95%的置信度保证损失的数额的最大值为7.95万元，以及要求在一个周期内的损失超过10万元的可能性不大于5%，那么初始投资额最多应为1257.86万元。

1 问题分析

要求概率，首先我们需要先确定所给的样本服从何种分布，于是先对数据进行可视化分析。作出频数直方图，然后对其进行拟合。由于大部分随机变量都是服从正态分布的，故我们可以建立模型观察它是否近似服从正态分布，再进行非参数检验即可，得到随机变量的分布函数后，我们就可以用概率论的相关知识求解有关问题了。

2 模型假设

（1）所给的数据具有随机性，可以反映该公司在过去一年内的收益额总体情况；（2）假设每年影响收益额分环境因素是稳定的；（3）假设每个周期内的收益额独立同分布；（4）假设收益率为定值，即投资额与收益额之间呈线性关系。

2.1 符号系统

T:周期数；1-α:置信度；μi：i个周期时的样本均值；σi：i个周期时的样本标准差；K：最大损失额；M0:初始投资额。

2.2 模型建立

2.3 一周期情况下的两种模型

2.3.1 模型一：正态分布法

由于大部分随机变量都服从正态分布，故我们考虑这255个交易日的日收益额是否服从正态分布，我们首先画出其频率直方图，发现它确实近似服从正态分布，再用皮尔逊χ2拟合检验法[1]验证其是服从正态分布；接着求出分布函数和概率密度函数，最后利用概率论知识求解。

1）我们利用matlab软件画出了频数直方图，并对该图进行拟合，得到拟合图，发现其近似服从正态分布。

2）我们再利用matlab软件[2]进行皮尔逊拟合检验

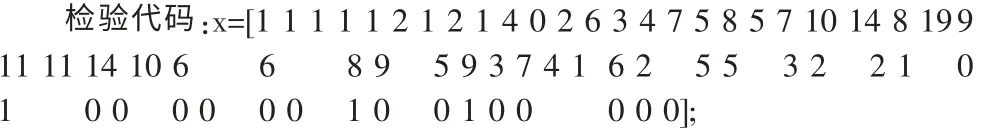
[h,p,stats]=chi2gof(x);运行后得到h=0，即接受原假设，也就是x服从正态分布；

3）由255个交易日的日收益额的统计数据，我们用Excel求得正态分布的参数μ=7.4863，σ=9.8520。

20世纪初分层教学之所以兴起，是由于当时美国面临大量移民儿童的涌入，学生背景各异，水平差距大，给统一教学带来了困难。而在当今社会，人口流动与免试就近入学政策的实行使我们看到了当时美国教学困境的缩影。

第一问：(1)求下一个周期内的损失的数额超过10万元的可能性，即求p{X-10}，其中X～N（7.4863，9.8522）,我们利用matlab软件输入命令[3]：normspec([-inf-10]，7.4863,9.852)，得到运行结果ans=0.037957，即p{X-10}=0.037957≈3.80%;(2)求解以95%的置信度保证损失的数额的最大值。要求以95%的置信度保证损失的数额不会超过多少，设最大损失额为K，则即求P{X-K}=0.95时的X值。要使P{X-K}=0.95，即等价于使P{X-K}=1-0.95=0.05，由此可得 K=1.645*σ-μ=1.645*9.852-7.4863=8.72万元。

第二问：设初始投资额为M0，由假设4得到，M0/1000=10/8.72，解得M0=1149.43万元，故如果要求在一个周期内的损失超过10万元的可能性不大于5%，那么初始投资额最多应为1146.79万元。

2.3.2 模型二：蒙特卡罗法[4]

题中已经给了255个数据，我们可以利用蒙特卡罗法，先对这255个数据进行理论分析，得到了这些数据的均值为7.4863，标准差为9.852，再通过模拟，将255个数据按一定的法则扩展成100000个数据，最后进行相关问题的求解。

第一问:（1）求下一个周期内的损失的数额超过10万元的可能性，即求p{X-10}

我们将根据均值和标准差，将255个数据扩展为100000个，再求这100000个随机数据中数额超过10万元的概率，我们用matlab软件（程序见附录1）得到p{X-10}=0.0391=3.91%

由于第一问中我们得到损失数额超过10万元的概率小于0.05，故要求以95%的置信度保证损失的数额的最大值，其值必然小于10万元，我们取它在（-10，10），以0.01为步长，找到概率为0.05的那个值，即为要求的最大值，我们用matlab软件解得ans=-8.89，即损失数额的最大值为8.89万元

第二问：由假设4，我们知初始投资额与日收益额之间为线性关系，故M0/1000=10/8.72，所以M0=10000/8.89=1124.86万元

2.3.3 两种模型的比较

首先比较两组模型的结果发现它们的结果是近似相等的，这说明两组模型均有一定准确度。对于模型一，我们由经验猜测其服从正态分布，并用理论证明了我们的猜想，在得到其服从正态分布后，我们运用概率论的相关知识以及matlab软件中的一些基本命令进行求解，得到了较为准确的结果；对于模型二，我们用蒙特卡洛法进行计算机随机数模拟，利用模拟的过程得到相应要求的概率或损失最大额。

由于计算机模拟产生的是随机数，其运算的结果必然不会每次相同，而有一定的范围，要使运算结果相对准确，就需要产生更多的随机数，即拓展的数据越大，得到的结果更准确，这样必然就增大了计算量，增加运算时间，所以我们认为模型一相对更好。

2.4 二周期情况

第一问：(1)求周期内的损失的数额超过10万元的可能性，即求p{X1+X2-10}：我们利用matlab软件输入命令：normspec([-inf-10]，14.9726,13.9328)，得到运行结果ans=0.0365，即p{X-10}=0.0365=3.65%;(2)同第一种情形的解法，得损失数额的最大值K=1.645*σ2-μ2=1.645*13.9328-14.9726=7.95万元；第二问：同第一种情形的解法：M0/1000=10/7.95，所以M0=1257.86万元.