卧螺式浮渣分离离心机两相数值模拟

朱明军，袁惠新，付双成，董连东（常州大学机械工程学院，江苏常州213000）

卧螺式浮渣分离离心机两相数值模拟

朱明军，袁惠新，付双成，董连东
（常州大学机械工程学院，江苏常州213000）

第一作者：朱明军（1988—），男，硕士研究生。E-mail zhumj07420418@126.com。

联系人：袁惠新，教授。E-mail yuanhuixin2000@126.com。

摘要：传统的卧式螺旋卸料离心机只能分离沉渣，不能分离浮渣。本文对一种分离轻质固体浮渣的卧螺离心机进行两相数值模拟研究，使用Pro-E软件建立三维模型，应用计算流体力学软件Fluent，基于Euler多相流模型，采用RNG k-ε湍流模型及多重参考系（MRF）方法，模拟分析了这种卧螺离心机内的固液两相体积分数分布以及操作参数和物性参数对流场和分离性能的影响。模拟结果表明：此卧螺离心机适用于高浓度、中粗粒子的分离；流体沉降分层比较明显，水在液池的外层，浮渣在内层；转速差总体上对分离性能影响不大，但不能过低或是过高，保持在30～70r/min是比较好的选择；进料浓度增加，颗粒沉降速度降低，分离效率会下降；小颗粒沉降速度底且易“反混”而分离性能差，较大颗粒沉降速度高，分离性能明显高于小粒径颗粒。

关键词：浮渣分离；卧螺离心机；数值模拟；分离性能

卧螺离心机作为一种高效分离设备，广泛应用于石油化工、建筑工程、生物医疗等行业。很多学者对其原理结构、设计计算以及其内部流体动力学规律进行了深入研究[1-2]，近年来一些研究者也对其进行了计算机数值模拟研究。

郑胜飞、于萍、刘京广等[3-5]对分离沉渣的普通卧螺离心机内部流场进行了数值模拟研究，其理论分析及模型建立均未考虑螺旋对于内部流场的影响，与实际工况相差较大，但对本文研究的浮渣式离心机提供了一定的模拟参考。

俞卫军[6]通过对普通固液分离卧螺离心机的三维流场数值模拟，分析研究了影响含油浮渣离心脱水效果的主要因素，但其主要是进行混凝实验，通过投加高分子絮凝剂使轻质浮渣聚集结块而沉降在转鼓内壁，提高普通卧螺离心机的处理能力。

以上所述普通卧螺离心机只能分离沉渣，而卧螺式浮渣分离离心机应用前景广阔，比如焦化厂中的冷焦废水除去轻质含油焦粉、“三泥”处理中含油浮渣脱水工艺、轻质纤维和塑料的回收利用等[7-10]。然而，到目前为止国内外在这方面的研究较少，尤其是在现今CFD模拟软件Fluent高速发展的时期，很少有人在这方面做过数值模拟研究，从而来更好地指导企业生产出较高性能的卧螺式浮渣分离离心机。

本文研究的浮渣分离离心机主要参考一种分离冰粒悬浮液的卧螺离心机[11]。其几何模型如图1所示，螺旋叶片在转鼓内的高度较低，轻质固体在液池的内层，重相液在外层，在转鼓柱段的内壁上沿轴向装设有相当数量的筋板，且在转鼓左端溢流口附近设有环形挡板以阻止轻质固体浮渣流向溢流口，减少液体的含渣量。

1　模型简介及边界条件

1.1模型简介

利用Pro-E三维建模软件建立的卧螺式浮渣分离离心机的三维模型见图2，其中在转鼓轴向方向上设置12块筋板，由于研究的是离心机的内部流场，所以这里将进料装置简化，直接将3个进料管连在锥段并与轴线平行，6个出液口在转鼓大端最左侧，环形挡板位于螺旋内筒距离转鼓左端面20mm处，厚度为5mm，结构尺寸见表1。对转鼓和螺旋采用T-grit方法创建的非结构化网格如图3所示，共划分出1778661个网格、3929398个面、386388个节点。

图1　卧螺式浮渣分离离心机几何模型

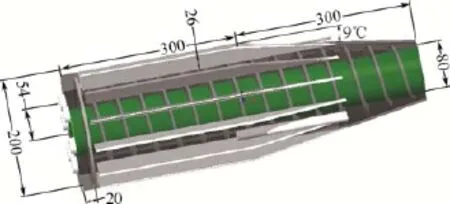
图2　浮渣分离离心机三维模型组装图及主要尺寸（单位：mm）

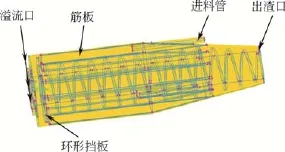
图3　浮渣分离离心机三维模型网格

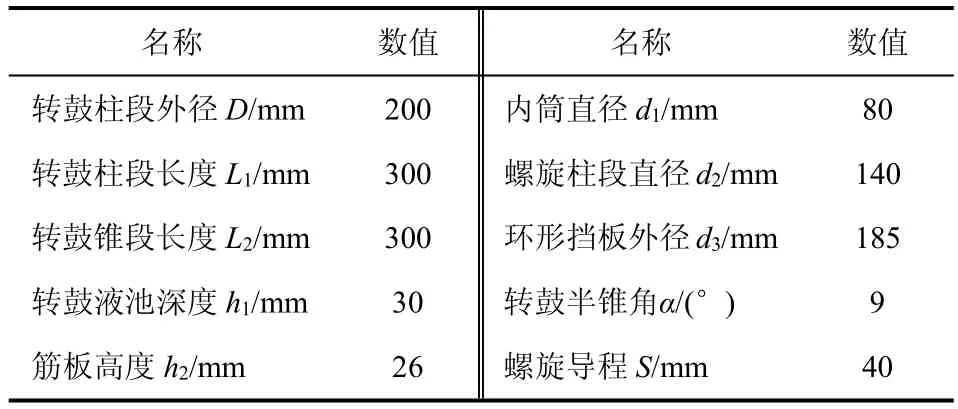
表1　卧螺式浮渣分离离心机几何模型基本尺寸

1.2边界条件

入口设定为速度入口边界，入口速度v=0.4m/s，方向垂直于入口方向，入口湍流强度为5%。除下文模拟的可变的操作参数和物性参数外，物料固液两相流基本参数及离心机基本运行参数有：液相介质为水，密度ρl=998kg/m3，黏度μl=0.001Pa⋅ s ；固相为硅颗粒，密度ρs=500kg/m3，黏度μs=1.72×10−5，固体颗粒粒径为1mm，固相所占流体体积分数为20%，转鼓转速为3500r/min，转速差为30r/min。出口边界设为自由出口边界。对于转鼓壁，设为无滑移条件，螺旋与筋板之间设置interface面，所有壁面上流体都满足速度无滑移条件。为分析方便，在z=0平面上，分别选择如图4所示的轴向位置150mm、250mm、265mm、350mm、420mm、450mm、580mm来进行研究分析。

1.3仿真计算

边界条件设置完之后导入到Fluent软件设置好参数开始进行数值模拟计算，整个流场在迭代了45000步左右之后，残差曲线基本达到收敛精度要求，出渣口渣的体积分数基本保持不变（图5），可以认为两相数值模拟基本收敛。

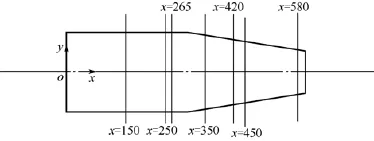
图4　卧螺离心机模型在z=0截面上的轴向位置截面图（单位：mm）

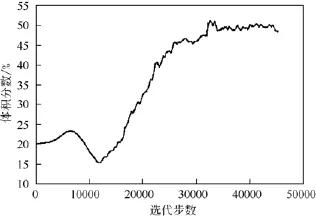
图5　出渣口渣的体积分数监测图

2　相的体积分数模拟结果分析

图6　z=0截面液相体积分数云图

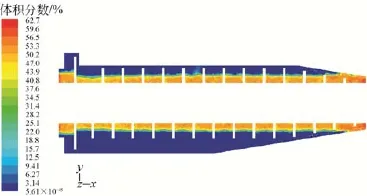
图7　z=0截面固相体积分数云图

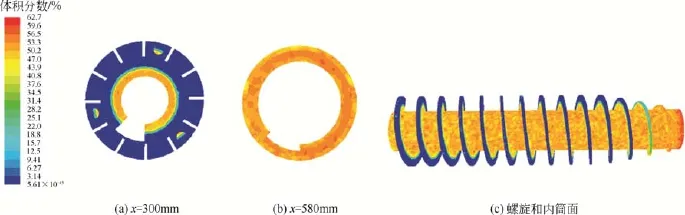
图8　不同截面固相体积分数分布云图

图6为z =0截面液相体积分数云图。从图6中可以清晰地看到液池的分层，液面基本平行于出液口外边缘位置，螺旋叶片伸入液面一定距离。图7和图8为不同截面固相体积分数云图，由于浮渣的密度小于液体水的密度，所以水在液池的外层，而内层是浮渣。在锥段离出渣口较近的区域以及出渣口位置，浮渣的体积分数维系在55%左右。

3　操作参数对流场以及分离性能的影响

3.1转速对滞后系数以及离心液压的影响

3.1.1转速对滞后系数的影响

当卧螺式浮渣离心机工作时，转鼓以及螺旋转动带动周围的液体及浮渣一起转动，流体的转动与转鼓转动并非一致，即存在滞后现象。这里研究相1即液体的滞后。为此，设转鼓转速为ω，自由液面的转速为ω0，通常用ω0/ω表征滞后量的大小，值越小，表明滞后越大。

图9是轴向位置为450mm、径向位置是70mm以及z=0点处的液体的转速、滞后系数与转鼓转速的模拟关系图，其中自由液面处液体的转速由公式ω0=vτ/r0（vτ为此点的切向速度，r0=0.07m）计算得到。从图9中可以看出，随着转鼓转速的增大，在转鼓的带动下，自由液面的转速逐渐增大，而滞后系数先是在0.75～1.05之间摆动，而当转鼓转速在4500r/min以上时，趋于稳定，大概为1.07。滞后系数变化不稳定，有时甚至超过1，主要是由于研究的点的径向位置为转鼓壁与螺旋内筒壁的中间处，流体流动时常也会受到螺旋转动的影响，而转鼓转速较高时，在转鼓旋转带动筋板一起以相同的速度高速旋转的作用下，流体的转动基本与转鼓保持一致。

3.1.2转速对离心液压的影响

物料中某一径向位置由离心作用产生的离心压力按公式（1）、式（2）计算。

当r0=0时，离心压力达到最大值。

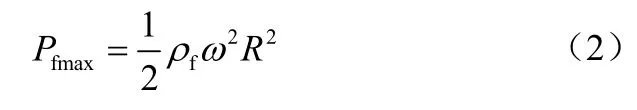
式中，ρf为液体的压力，Pa；ω为转鼓转速，r/min；R为转鼓半径，mm；r0为自由液面的径向位置，mm。

此最大值发生在转鼓的鼓壁处，即图10（轴向位置为450mm、径向位置是100mm以及z=0）中的离心液压值。从图10中也可以看出，随着转鼓转速的增大，相1液体的动压和混合物的静压基本成抛物线的变化规律，即二次方正增长，且液体的动压与理论值接近。这体现了转鼓壁处的压力主要是来自液体高速旋转运动对鼓壁所产生的压力，而鼓壁处混合物的静压要明显低于此动压值。

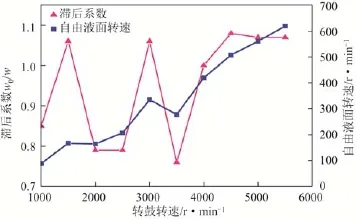
图9　转鼓转速-滞后系数/自由液面转速关系

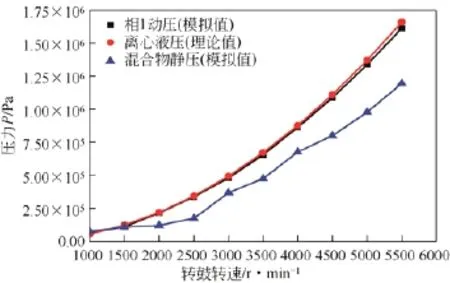
图10　转鼓转速-相1动压/混合物静压关系

3.2操作参数对流场以及分离性能的影响

3.2.1分离效率的定义

分离性能用分离效率来评价。根据物料平衡，悬浮液中的固相质量M应等于沉渣中固相质量Mc与分离液中固相质量Mf之和，即式（3）。

因此，分离总效率的定义为式（4）。总效率又称固相回收率[1]。

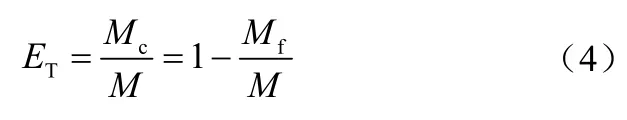
3.2.2转速差对分离性能的影响

转速差是指转鼓转速与螺旋输送器转速之差，也即两者的相对速度。转速差直接影响排渣能力、上清液质量、泥饼干度等。在两相数值模拟中改变转速差，可以得出图11，即转速差与出渣口固渣含湿率和固相回收率的关系。从图11中可以看出，转速差总体上对固渣含湿率和固相回收率影响不大。当转速差在10～30r/min时，随着转速差的增大，出渣含湿率增大，固相回收率降低。这是因为较低的转速差使得物料在转鼓中的停留时间增长，处理能力降低，使浮渣未被及时从排渣口排出，就反流回沉降区，从上清液中流失，导致上清液质量差。此外，转速差过低，可能导致离心机损坏。式（5）为螺旋转矩[12]公式。

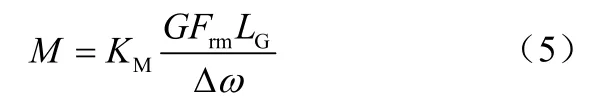
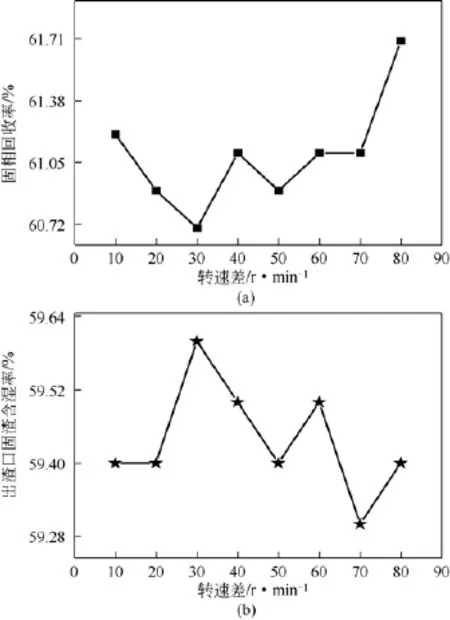
图11　转速差对分离性能的影响

式中，KM为磨损系数；Frm为脱水区的平均分离因数，；LG为脱水区的轴向长度，mm； Δω为转速差，r/min。

从式（5）可以看出，M与Δω成反比，当转速差很小时，螺旋受到的扭矩将很大。甚至会由于螺旋阻力过大，螺旋受到的扭矩过大而损坏差速器。

而当转速差在70r/min以上时，过大的转速差会使得沉渣脱水时间缩短，脱水后沉渣含湿率增大。所以转速差在30～70r/min是比较好的选择。

3.2.3进料固相体积分数对沉降速度以及分离性能的影响

3.2.3.1进料固相体积分数对沉降（径向）速度的影响

脱水用卧螺离心机半锥角α=9°～12°，一般用于中粗粒子和高浓度较易分离的悬浮液，本文研究的脱水用卧螺式浮渣分离离心机α=9°，适用于高浓度悬浮液的分离，所以本文模拟的固相进料体积分数在10%～60%之间变化。

假如颗粒在流体中的分布为均匀的四面体分布，则颗粒间距l与浓度的关系为式（6）[13]。

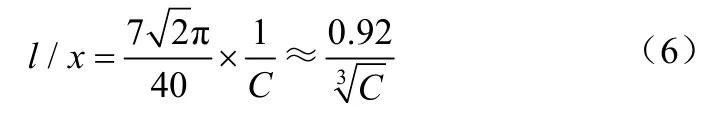
式中，C为颗粒的体积浓度；l/x为间距与粒径之比。

当浓度增加，l/x减小，沉降过程中，颗粒间发生摩擦、碰撞而失去动能，即增加了阻力系数，从而沉降速度降低。

浓度对颗粒沉降速度的影响可以用式（7）考虑[13]。

式中，ut为未考虑浓度影响的沉降速度；uts为考虑了浓度影响后的沉降速度；n为颗粒雷诺数Rep的函数（如图12），Rep<0.3时n=4.65，Rep>1000 时n=2.33。

由式（7）得出，浓度对颗粒沉降速度的影响大致呈n次方的负比例关系，即随着浓度的增加，沉降速度逐渐降低。从图13模拟结果分析也可以看出，径向速度随着径向位置基本成抛物线的变化规律，而随着进料固相浓度的增加，颗粒的沉降速度大都逐渐减小。

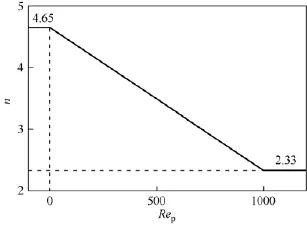
图12　指数n和颗粒雷诺数之间的关系

3.2.3.2进料固相体积分数对分离性能的影响

从图14模拟结果分析可以看出，进料固相体积分数总体上对进料口固渣含湿率、出渣含湿率和固相回收率影响不大。随着进料固相体积分数的增大，由于进料浓度的增加，所以使得进料口固渣含湿率逐渐降低。而固相回收率先是缓慢增加，而当进料体积分数在50%以上时，其迅速降低。一方面这是由于如前文分析指出，浓度增加，颗粒沉降速度降低，使得颗粒在转鼓内的停留时间增长，颗粒未及时沉降而从溢流口跑出，从而影响输渣降低了固相回收率；另一方面，浓度过高会使螺旋输送器承受载荷加大，从而影响其输渣能力，降低分离性能。此外，由图14数值模拟结果分析可以看出，出渣含湿率受固相浓度的影响不大，维系在59%～60%之间。

3.2.4颗粒粒径对沉降速度以及分离性能的影响

3.2.4.1颗粒粒径对沉降（径向）速度的影响

颗粒的沉降速度可表达为如式（8）、式（9）的颗粒粒度x的函数[13]。

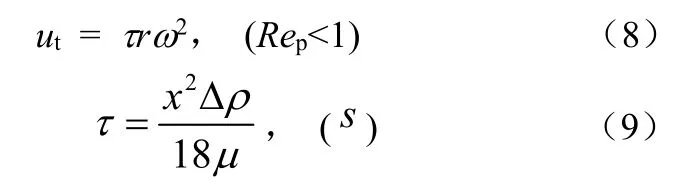
式中，τ为“分割常数”或“时间常数”；rω2为离心加速度；x为颗粒粒径；Δρ（负）为颗粒与介质的密度差，Δρ=ρp−ρf（其中ρp为颗粒的密度，ρf为介质的密度）；μ为颗粒的黏度。

从式（8）和式（9）可以得出，在其余参数不变的情况下，颗粒的沉降速度与颗粒粒径的二次方成正比。通过数值模拟分析，从图15可以看出，0.005mm颗粒和0.05mm颗粒的沉降速度明显低于2.5mm和3mm颗粒的沉降速度，甚至0.005mm颗粒的大部分径向速度为正，这就是下文要分析的“反混”现象。此外，2.5mm颗粒和3mm颗粒分别在径向位置大于50mm和58mm时的径向速度基本为零，说明此两种颗粒分别位于这两个径向位置以下，在其以上几乎没有颗粒。

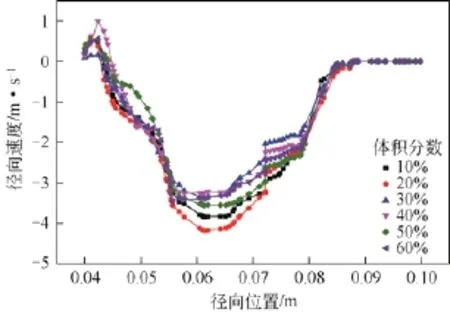
图13　进料体积分数对固相径向速度的影响（x=265mm截面）

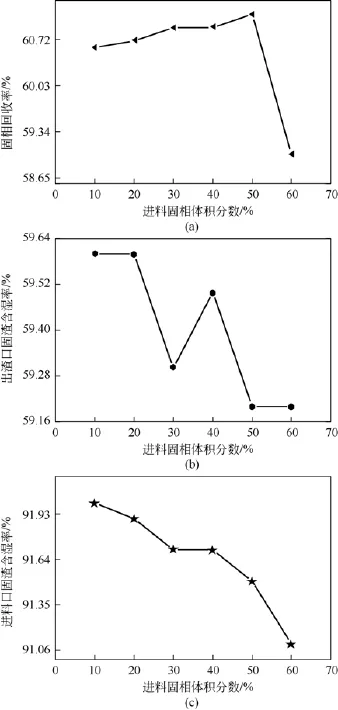
图14　进料固相体积分数对分离性能的影响

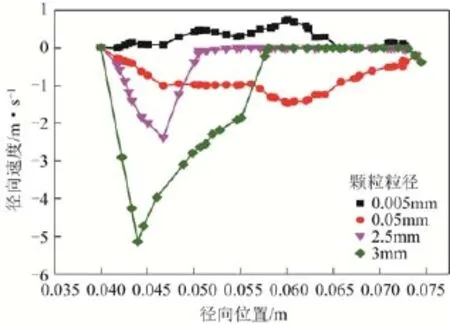
图15　颗粒粒径对固相径向速度的影响（x=150mm截面）

3.2.4.2颗粒粒径对分离性能的影响

从图16可以看出，颗粒粒径对出渣含湿率和固相回收率的影响比较大。粒径为0.005mm、0.01mm以及0.02mm的颗粒由于出液口和出渣口含渣量较低（见图17），所以固相回收率和出渣含湿率较高。当颗粒粒径在0.005～0.1mm之间变化时，随着颗粒粒径的增大，出渣含湿率逐渐增大，而固相回收率基本上逐渐减小，且总体上出渣含湿率较高，而固相回收率除了0.005mm、0.01mm以及0.02mm外都比较低。显然，基于前文的分析，过于细微的颗粒在离心机中的沉降速度会比较小从导致分离效率的下降。

另一方面，时间常数小的颗粒不仅沉降速度小，而且对湍流也很敏感，即使颗粒已经沉降了，也很容易地被卷起——反混（remixing），导致分离效率下降。图17和图18分别为0.005mm颗粒的固相体积分数分布图和径向速度矢量图，从中可以明显看出这一现象。其中图18为x=150～250mm截面y轴正方向上的局部放大图，图中的蓝色箭头代表颗粒径向速度为负值，其余则为正值，说明部分颗粒朝转鼓壁方向运动，出现了反混。

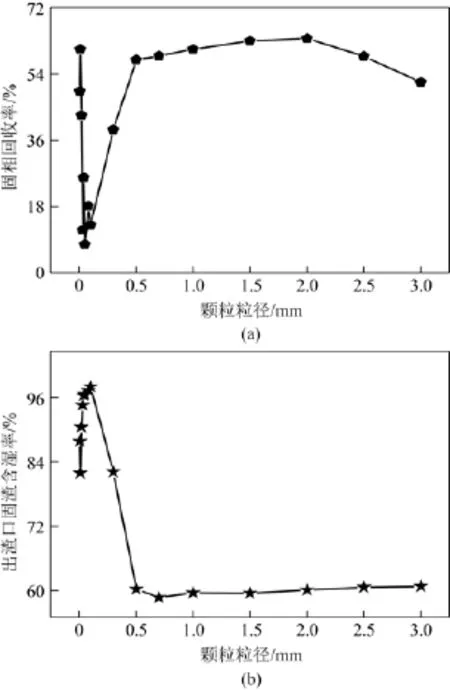
图16　颗粒粒径对分离性能的影响

图17　z=10mm截面固相体积分数分布云图

图18　z=10mm截面固相径向速度矢量图（局部放大图）

而当颗粒粒径在0.1～0.5mm之间变化时，随着颗粒粒径的不断增大，出渣含湿率显著降低，而固相回收率也明显提高。当颗粒粒径在0.5mm以上时，固相回收率较高，基本维系在54%以上，出渣含湿率也相对较低，保持在60%左右，分离效率相对小粒径颗粒显著提升（见图16模拟分析）。

前文已经说明本文研究的卧螺式浮渣分离离心机适用于高浓度、中粗离子的分离，所谓中粗粒子是指颗粒粒径在0.1mm以上乃至几个毫米[13]，以上模拟结果也证实了这点。

4　结论

本文采用Fluent软件中的RNG k-ε湍流模型和多重参考系（MRF）方法以及Euler多相流模型，对一种卧螺式浮渣分离离心机进行了两相数值模拟研究，模拟分析了这种卧螺离心机内的固液两相体积分数分布以及操作参数和物性参数对流场和分离性能的影响，得到如下结论。

（1）流体沉降分层比较明显，可以清楚地看到液面，水和浮渣的体积分数分布云图基本达到了预期效果，浮渣在液池的内层，水在外层。在锥段离出渣口较近的区域以及出渣口位置，浮渣的体积分数维系在55%左右。

（2）流体流动受到转鼓和螺旋转动的双重影响，当转鼓转速较高时，在转鼓旋转带动筋板一起以相同速度高速旋转的作用下，流体的转动基本与转鼓保持一致。转鼓壁处的压力主要是来自相1即液体高速旋转运动对鼓壁所产生的压力，而鼓壁处混合物的静压要明显低于此动压值。

（3）转速差总体上对分离性能影响不大，但不能过低或是过高，保持在30～70r/min是比较好的选择。进料浓度增加，颗粒沉降速度降低，分离效率会下降。小颗粒沉降速度底且易“反混”而分离性

能差，较大颗粒沉降速度高，分离性能明显高于小粒径颗粒，说明此卧螺离心机适用于高浓度、中粗粒子的分离。

参 考 文 献

[1] 孙启才，金鼎五.离心机原理结构与设计计算[M].北京：机械工业出版社，1987.

[2] 袁惠新.分离过程与设备[M].北京：化学工业出版社，2008.

[3] 郑胜飞，任欣，谢林君.卧螺离心机流场的三维数值模拟[J].轻工机械，2009，27（6）：26-29.

[4] 于萍，林苇，王晓彬，等.卧螺离心机离心分离场速度仿真分析[J].机械工程学报，2011，47（24）：151-157.

[5] 刘京广.卧螺离心机流场数值模拟及转鼓锥角研究[D].长春：吉林大学，2011.

[6] 俞卫军.含油浮渣离心脱水效果的强化研究[D].上海：华东理工大学，2007.

[7] Xu Z，Wang Z，Kung J，et al.Separation and characterization of foulant material in coker gas oils from Athabasca bitumen[J].Fuel，2005，84（6）：661-668.

[8] 王毓仁，顾薇琼.炼厂含油污泥的离心脱水技术的探索[J].石油炼制与化工，2003，34（1）：49-55.

[9] 刘学东，吴仲岿，柳俊，等.炼厂焦化装置含硫废水除焦粉中试研究[J].新技术新工艺，2012（9）：46-48.

[10] 谭万将.旋流分离小密度差塑料(PET/PVC)过程的研究[D].常州：常州大学，2012.

[11] Shapiro L，Darby U.Screw-type solids discharge centrifuge having means to discharge light solids：US，415435[P].1964.

[12] 毕秦岭，张博松.螺旋沉降离心机扭矩高的原因分析及改进[J].石化技术与应用，2001，19（4）：245-247.

[13] 袁惠新，冯骉.分离工程[M].北京：中国石化出版社，2001.

研究开发

研究开发

Two-phase numerical simulation research in a decanter centrifuge of separating floating sludge

ZHU Mingjun，YUAN Huixin，FU Shuangcheng，DONG Liandong
（School of Mechanical Engineering，Changzhou University，Changzhou 213016，Jiangsu，China）

Abstract：Traditional decanter centrifuge is only used to separate heavy sludge rather than floating sludge.This research developed a two-phase numerical simulation on a decanter centrifuge in separating light solid floating sludge.The three dimension software Pro-E was used to build the 3D model.The computational fluid dynamics software Fluent was applied to analyze volume fraction distribution of the solid and liquid phase as well as the effects of operating conditions and fluid parameters on flow field and separation properties.The simulation was based on Euler multiple phase flow model and RNG k-ε turbulence model in a multiple coordinate reference system.The simulation results showed that the decanter centrifuge can be used to separate high density and middle-coarse particles；the fluid settling lamination was obvious and water was in the inner side while floating sludge outside of cistern；there was little effect of rotation speed discrepancy on separation properties.Rotation speed discrepancy in the range of 30—70r/min was optimal.With the increase of the feed concentration，particles’setting velocity and separation efficiency decreased.Low setting velocity for small particles resulted in less separation efficiency and coarse particles had higher separation capabilities because of quick setting velocity.

Key words：light floating sludge separation；decanter centrifuge；numerical simulation；separation properties

基金项目：科技部科技型中小企业创新基金（08C26213200648）及江苏省2013年度高校研究生科研创新计划（CXLX13_724）项目。

收稿日期：2014-07-21；

DOI：10.16085/j.issn.1000-6613.2015.02.007

文章编号：1000–6613（2015）02–0336–08

文献标志码：A

中图分类号：TK-9

修改稿日期：2014-09-16。