Extended trajectory shaping guidance law considering a first-order autopilot lag
2015-04-22WANGHui王辉WANGJiang王江CHENGZhenxuan程振轩
WANG Hui (王辉), WANG Jiang (王江), CHENG Zhen-xuan (程振轩)
(1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.China North Industries Group Corporation, Beijing 100821, China)
Extended trajectory shaping guidance law considering a first-order autopilot lag
WANG Hui (王辉)1, WANG Jiang (王江)1, CHENG Zhen-xuan (程振轩)2
(1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.China North Industries Group Corporation, Beijing 100821, China)
To satisfy the terminal position and impact angel constraints, an optimal guidance problem was discussed for homing missiles. For a stationary or a slowly moving target on the ground, an extended trajectory shaping guidance law considering a first-order autopilot lag (ETSGL-CFAL) was proposed. To derive the ETSGL-CFAL, a time-to-go -nth power weighted objection function was adopted and three different derivation methods were demonstrated while the Schwartz inequality method was mainly demonstrated. The performance of the ETSGL-CFAL and the ETSGL guidance laws was compared through simulation. Simulation results show that although a first-order autopilot is introduced into the ETSGL-CFAL guidance system, the position miss distance and terminal impact angle error induced by the impact angle is zero for different guidance time.
extended trajectory shaping guidance law; time-to-go; first-order autopilot; guidance performance
Linear optimal guidance problems have been studied since the 1960s in the last century. During this period, based on different terminal constraints, several different linear optimal guidance laws have been proposed[1-12]. In these guidance laws, the optimal guidance law with impact angle constraint (OGLIAC) attracted more attentions. As mentioned in Refs.[4-8], to enhance the missile’s warhead effectiveness, many attacking missions have additional requirements on the terminal impact angle. For example, for antitank missiles, a near-vertical attacking direction is often designed to enhance the attacking effect on the armored vehicles; and for some anti-ship missiles, a side-plane attacking technology is often used to make the missile attack the side part of the ship in a lateral-vertical direction.
Terminal impact angle control problem has been an important area of research in the homing missile guidance in recent years. In Ref.[4], Zarchan proposed an optimal guidance law called trajectory shaping guidance law (TSGL), which can also control the terminal impact angle. With the assumption of small angle for the line of sight (LOS) angle and the flight path angle, the TSGL is equivalent to the OGLIAC[4, 6-8]. In 1998, the TSGL was defined in the desired terminal line of sight frame and the guidance performance of which was also demonstrated by Ben-Asher and Yaesh[5]. During 2003-2005, the guidance performance of TSGL with a first-order autopilot was studied by Ryoo et al[6-7]. In 2013, for a stationary or a slowly moving target on the ground, a new form of time-to-go polynomial guidance law with impact angle constraint was proposed by Kim and Lee[9-10]. The new guidance law provides a new angle of view to study the optimal guidance problem with impact angle constraint.
As mentioned above, the TSGL or OGLIAC was usually derived using the linear quadratic optimal control theory with some given terminal constraints, where the weighting functionR(t) in the object function was defined as the traditional form, i.e.,R(t) was set as a constant value one[4-8]. Correspondingly, the guidance law can be called as the conventional TSGL (CTSGL). However, in 2006, a more generalized form of the CTSGL, namely, the extended TSGL (ETSGL), was proposed by Ohlmeyer, Ryoo, et al., where the weighting function was extended to a new form of time-to-go -nth power[11-12]. This promotes the corresponding research work of the optimal guidance laws to a more widely research area[9-13].
In this paper, considering a first-order autopilot lag, the extended weighting function found in Refs.[11-12] is adopted to derive the ETSGL using three different methods and the method of the Schwartz inequality is mainly demonstrated. The proposed guidance law is called extended trajectory guidance law considering a first-order autopilot lag (ETSGL-CFAL). Finally, the guidance performance of the ETSGL-CFAL is analyzed.
1 Missile’s longitudinal motion equations considering a first-order autopilot lag
According to Ref.[14], for a stationary or a slowly moving target, the longitudinal equations of missile’s motion can be expressed as
(1)
wherey,V,θandamdenotes the missile position, velocity, flight path angle and acceleration response, respectively. Under the assumption thatVis constant andθis small angle, Eq.(1) can be linearized as
(2)
Thetransferfunctionofafirst-orderaccelerationautopilotcanbeexpressedas
am(s)/ac(s)=1/(Tgs+1)
(3)
whereacmeans the missile acceleration command andTgdenotes the time constant of the autopilot. Rewrite Eq.(3) as the form of differential equation, one obtains
(4)
CombiningEqs.(2) (4),themissile’slongitudinalmotionequationsconsideringafirst-orderautopilotlagcanbewrittenas
(5)
where
(6)
(7)
In Eq.(7),y(tf) is the missile position at the terminal timetf,θ(tf) is the terminal flight path angle andam(tf) is the missile terminal acceleration response. The desired values ofy(tf),θ(tf) andam(tf) areyf,θfandaf, respectively.
2 Derivation of the ETSGL-CFAL using three different methods
2.1 Derivation of the ETSGL-CFAL using the linear quadratic optimal control theory
2.1.1 Using the optimal method in Ref.[7]
Let us first consider the following optimal control problem: subject to Eq.(5), findu(t) to minimize the cost functionJwhich is defined as
(8)
whereSf≥0,R(t)>0,t0is the initial time. The solution of the optimal control problem shown in Eq.(5) and Eq.(8) is given by Ref.[7], that is
u(t)*=-R(t)-1BTΦT(tf,t)Sf[x(tf)-xf]
(9)
whereΦ(tf,t) is the state transition matrix fromttotfand the expression of x(tf)-xfis given by
x(tf)-xf=
[Φ(tf,t)x(t)-xf]
(10)
According to Eq.(6), the weighting funtionR(t) and the terminal state weighting matrix Sfare chosen as
(11)
wheretf-t=tgo. The estimation method of time-to-go and the influence of time-to-go estimation errors on the guidance performance have been studied by Ryoo et al[6-7, 12]. Therefore, we assume that time-to-go is exactly known in this paper.

According to Eq.(10), we define C as
(12)
where the expressions ofM11,M12,M21andM22are given by
D1=Tg(e-tgo/Tg+tgo/Tg-1),D2=1-e-tgo/Tg
(13)
(14)
(15)
(16)
(17)
CombiningEqs.(5)-(17)andaftercomplexcalculations,oneobtainstheoptimalguidancelaw:
W2θ(t)+W3θf+W4am(t)]
(18)
whereW1,W2,W3andW4are defined as
W1=(1/Δ)(s1D1M22-s2D2M21)
(19)
W2=(1/Δ)[s1D1(M22Vtgo-M12)]+
(1/Δ)[s2D2(M11-M21Vtgo)]
(20)
W3=(1/Δ)(s1D1M12-s2D2M11)
(21)
W4=(Tg/Δ)[s1D1(M22D1-M12D2/V)]+
(Tg/Δ)[s2D2(-M21D1+M11D2/V)]
(22)
(23)
AccordingtoEq.(18),wesets1→∞,s2→∞, the final expression of the ETSGL-CFAL can be simplified as
W′3)Vθ(t)-W′3Vθf+Tg(D1W′1+D2W′3)am(t)}
(24)
2.1.2 Using the optimal method in Ref.[12]
Rewrite the terminal constraints Eq.(7) as the form of matrix, that is
(25)
Neglect the terminal state constraint in Eq.(8), then Eq.(8) can be simplified as
R(t)=1/(tf-t)n,n≥0
(26)
According to Ref.[12], the optimal solution is given by
u(t)*=-R(t)-1BTFG-1[E-FTx(t)]
(27)
where the matrices F and G are given by
(28)
Substituting Eqs.(6) (25) into Eq.(28), we have
(29)
(30)
where G is a 2×2 matrix.
Substituting Eqs.(6) (25) (29) (30) into Eq.(27), we finally have the ETSGL-CFAL, which is the same with Eq.(24).
2.2 Derivation of the ETSGL-CFAL using the Schwartz inequality
The general solution of the state space
Eq.(5) at the final time is given by[4]
(31)
whereΦ(t) is the fundamental matrix related to the matrix A according to
Φ(t)=L-1[(sI-A)-1]
(32)
From Eqs.(6) (32),Φ(tf-t) is found to be
(33)
SubstitutingEqs.(6) (7) (33)intoEq.(31),weget
(34)
Multiplyingouttheprecedingtwomatrixequationsyields
(35)
WestillwanttominimizetheextendedcostfunctiondefinedinEq.(26)subjecttothespecifiedterminalpositionandterminalimpactangle,thatis
y(tf)=yf,θ(tf)=θf
(36)
For convenience, let us first define
f1=y(tf)-y(t)-Vtgoθ(t)-
(37)
(38)
Thus,Eq.(35)canbewrittenas
(39)
InordertocombineEq.(39)intooneequation,wefirstdefineanewvariableσand then we have
(40)
IfweapplytheSchwartzinequalitytoEq.(40),weget
(41)
TheleftpartofinequalityEq.(40)isequivalenttotheextendedcostfunctionEq.(26)andwillbeminimizedwhentheequalitysignholds.UsingtheSchwartzinequality,theequalitysignholdsas
a′c(t)=C(h1-σh2)
(42)
whereCis a constant. Therefore, when the equality sign holds, we have
(43)
Forconvenience,wedefinethefollowingnewvariables
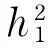
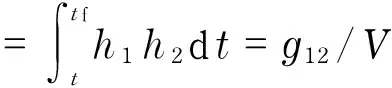

(44)
Thus,Eq.(43)canberewriteas
(45)
Defineσ′=σ/Vand then Eq.(45) can be expressed as
(46)
BytakingthederivativeofEq.(46)withrespecttoσand setting the result to zero, we get the optimalσ′ that minimizes Eq.(46), that is
σ′=(f2g11-f1g12)/(f2g12-f1g22)
(47)
Substituting Eq.(42) intof1in Eq.(39) and solving for the constantC, one obtains
C=f1/(g11-σ′g12)
(48)
And then, Eq.(42) can be expressed as
a′c(t)=f1(h1-σh2)/(g11-σ′g12)
(49)
Substituting Eq.(47) into Eq.(49) and after some algebra yields
(50)
SubstitutingEqs.(37) (44)intoEq.(50),weobtainthefinalexpressionoftheETSGL-CFAL,whichisalsothesamewithEq.(24).
Asshownintheabovetwosubsections,thethreedifferentderivationmethodsresulttothesameETSGL-CFAL.
ComparedwithCTSGLandETSGL,ETSGL-CFALisamoregeneralizedform.IfweneglectthetimeconstantTg, i.e., the autopilot is lag-free, ETSGL-CFAL will reduce to ETSGL and if we setTg=0 andn=0 simultaneously, ETSGL-CFAL will directly reduce to CTSGL.
2.3 Expression of the ETSGL-CFAL in engineering application

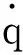
(51)

(52)
DefinesomenewgainsoftheETSGL-CFALas
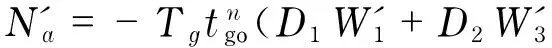
(53)
Combining Eqs.(24) (51) (52) yields
(54)
Eq.(54)istheexpressionoftheETSGL-CFALforengineeringapplicationinmissileguidance.FortheETSGL,Eq.(53)reducesto
N′p=2(n+2),N′θ=(n+1)(n+2),N′a=0
(55)
and then the ETSGL can be written as
(56)
3 Analysis of the normalized acceleration and normalized miss induced by the impact angle
For comparison, we consider both the ETSGL-CFAL and ETSGL guidance laws. Fig.1 gives the block diagram of the ETSGL-CFAL guidance system. As the gains of Eq.(55) are chosen, the ETSGL-CFAL guidance system can be simplified to the ETSGL guidance system with a first-order autopilot. In Fig.1, two constraints are considered, i.e., the desired missile positionyfand the desired impact angleθf. Simulation parameters of Fig.1 are given in Tab.1.

Fig.1 Guidance system of the ETSGL-CFAL/ETSGL
Tab.1 Simulation parameters

Parameteryf/mθf/(°)V/(m/s)Tg/stf/sValue0-30,-603000.510
Simulation results of the trajectories and LOS angles forθf=-30° andθf=-60°, respectively, are shown in Fig.2 and Fig.3. It can be seen that for the ETSGL-CFAL/ETSGL, both the curves of the trajectories and LOS angles are similar if a small indexnis chosen, for example,n=0; however, a large indexn, for example,n=1, will result in a higher trajectory for the ETSGL. Correspondingly, for the ETSGL-CFAL, a lower trajectory will be got whennis chosen as a large value.
Fig.4 gives the normalized acceleration commands of the ETSGL-CFAL/ETSGL induced by the impact angleθf. Fig.4 shows that it will result in an abrupt increase in the acceleration command at the final time if we introduce an autopilot lag into the ETSGL guidance system and this will lead to undesired position miss distance and impact angle error (as shown in Fig.5 and Fig.6), especially when the system total guidance timetfis not enough. The reason is that the ETSGL is only optimal for the lag-free autopilot and if we introduce into a first-order autopilot, the ETSGL is not optimal. However, the ETSGL-CFAL is also optimal at the existence of the first-order autopilot, and the acceleration command of which will approach to zero at the final guidance time (Fig.4). Thus, although a first-order autopilot was introduced into the ETSGL-CFAL system, there is no miss distance and terminal impact angle error as shown in Fig.5 and Fig.6.
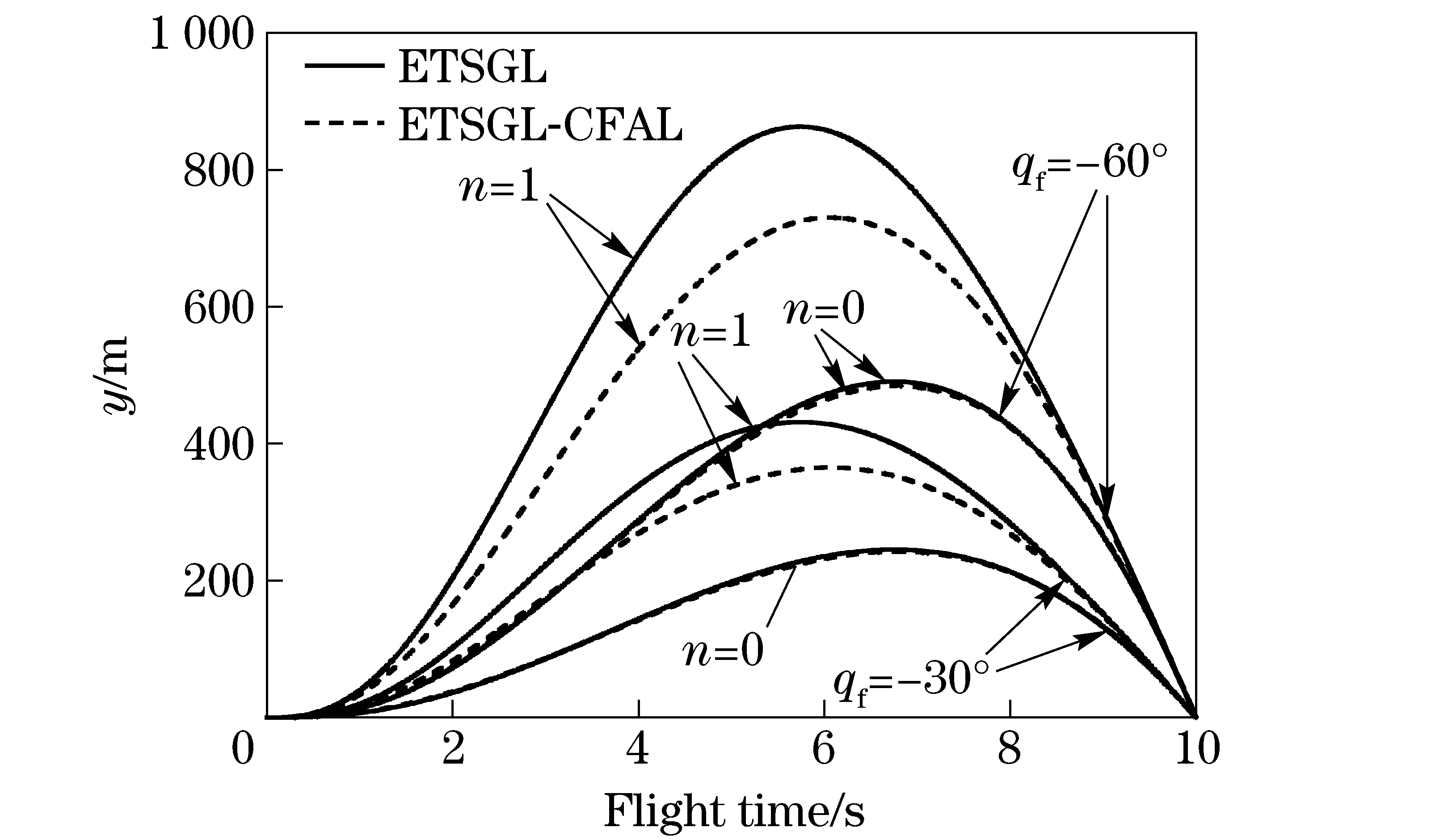
Fig.2 Trajectories for different θf

Fig.3 LOS angle q for different θf

Fig.4 Normalized acceleration commands induced by θf

Fig.5 Normalized position miss distance induced by θf

Fig.6 Normalized terminal impact angle error induced by θf
4 Conclusions
① Using a time-to-go weighted object function and considering a first-order autopilot lag, for a stationary or slowly moving target, an extended trajectory shaping guidance law, called ETSGL-CFAL in this paper, is proposed.
② Three different methods are adopted to derive the ETSGL-CFAL: two based on the linear optimal control theory and one based on the Schwartz inequality.
③ Performance of the ETSGL-CFAL and the ETSGL guidance laws are compared through simulation. Simulation results show that for different guidance times, although a first-order autopilot is introduced into the ETSGL-CFAL guidance system, there is no miss distance and terminal impact angle error induced by the impact angle.
[1] Kim B S, Lee J G, Han H S. Biased PNG law for impact with angular constraint [J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277-288.
[2] Ratnoo A, Ghose D. Impact angle constrained interception of stationary targets [J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1816-1821.
[3] Ratnoo A, Ghose D. State dependent Riccati equation based guidance law for impact angle constrained trajectories [J]. Journal of Guidance, Control, and Dynamics, 2009, 32(1): 320-325.
[4] Zarchan P. Tactical and strategic missile guidance[M]. 5th ed. Progress in Astronautics and Aeronautics, 2007: 541-569.
[5] Ben-Asher J Z, Yaesh I. Advances in missile guidance theory[M]. [S.l.]: American Institute of Aeronautics and Astronautics, Inc., 1998:25-88.
[6] Ryoo C K, Cho H, Tahk M J. Close-form solutions of optimal guidance with terminal impact angle constraint [C]∥Proceedings of IEEE International Conference on Control Application, Istanbul, Turkey, 2003: 504-509.
[7] Ryoo C K, Cho H, Tahk M J. Optimal guidance laws with terminal impact angle constraint [J]. Journal of Guidance, Control and Dynamics, 2005, 28(4): 724-732.
[8] Ryoo C K, Cho H, Tahk M J. Energy optimal waypoint guidance synthesis for antiship missiles [J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1):80-95.
[9] Kim T H, Lee C H, Tahk M J, et al. Time-to-go polynomial guidance with trajectory modulation for observability enhancement [J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 55-73.
[10] Lee C H, Kim T H, Tahk M J, et al. Polynomial guidance laws considering terminal impact angle and acceleration constraints [J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(1): 74-92.
[11] Ohlmeyer E J, Phillips C A. Generalized vector explicit guidance [J]. Journal of Guidance, Control and Dynamics, 2006, 29(2): 261-268.
[12] Ryoo C K, Cho H, Tahk M J. Time-to-go weighted optimal guidance with impact angle constraints [J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 14(3): 483-492.
[13] Wang H, Lin D F, Cheng Z X, et al. Optimal guidance of extended trajectory shaping [J]. Chinese Journal of Aeronautics, 2014,27(5):1259-1272.
[14] Qian X F, Lin R X, Zhao Y N. Missile aviation mechanics [M]. Beijing: Beijing Institute of Technology Press, 2008: 28-74. (in Chinese)
(Edited by Wang Yuxia)
10.15918/j.jbit1004-0579.201524.0302
TJ 765.3 Document code: A Article ID: 1004- 0579(2015)03- 0291- 07
Received 2013- 12- 01
Supported by the National Natural Science Foundation of China (61172182)
E-mail: wh20031131@126.com
猜你喜欢
杂志排行
Journal of Beijing Institute of Technology的其它文章
- Anti-hypertensive effects of rosiglitazone on renovascular hypertensive rats: role of oxidative stress and lipid metabolism
- On a novel non-smooth output feedback controller for the attitude control of a small float satellite antenna
- New model reference adaptive control with input constraints
- Facial expression recognition with contextualized histograms
- Length estimation of extended targets based on bistatic high resolution range profile
- Joint receiving mechanism based on blind equalization with variable step size for M-QAM modulation
