New model reference adaptive control with input constraints
2015-04-22WUWenbin武文斌GENGQingbo耿庆波FEIQing费庆HUQiong胡琼
WU Wen-bin(武文斌), GENG Qing-bo(耿庆波), FEI Qing(费庆),HU Qiong(胡琼)
(School of Automation, Beijing Institute of Technology, Beijing 100081, China)
New model reference adaptive control with input constraints
WU Wen-bin(武文斌), GENG Qing-bo(耿庆波), FEI Qing(费庆),HU Qiong(胡琼)
(School of Automation, Beijing Institute of Technology, Beijing 100081, China)
A new scheme of adaptive control is proposed for a class of linear time-invariant (LTI) dynamical systems, especially in aerospace, with matched parametric uncertainties and input constraints. Based on a typical and conventional direct model reference adaptive control scheme, various modifications have been employed to achieve the goal. “Composite model reference adaptive control”of higher performance is seamlessly combined with “positiveμ-mod”, which consequently results in a smooth tracking trajectory despite of the input constraints. In addition, bounded-gain forgetting is utilized to facilitate faster convergence of parameter estimates. The stability of the closed-loop system can be guaranteed by using Lyapunov theory. The merits and effectiveness of the proposed method are illustrated by a numerical example of the longitudinal dynamical systems of a fixed-wing airplane.
model reference adaptive control; input constraints; flight control
Adaptive control was developed essentially to process control with parametric uncertainties, in which model reference adaptive control (MRAC)[1-6], as an effective control methodology, has been maturely applied to flight control. Among them, an improved composite model reference adaptive control (CMRAC)was suggested, in which the direct and indirect adaptive control interacts to result in an extremely small tracking error[7]. Furthermore, bounded-gain forgetting (BGF)[8], which has also been observed to lead to improve transients, and make parameters converge faster.
However if MRAC is directly used in the condition with input constraints, field experience implies instability with large transient errors or oscillations, in short, the stability of the designed control system will severely deteriorate. Among all has been done, a design scheme called “anti-windup” was introduced in a non-adaptive scheme[9]. The main idea of the design is that as the signals of the open-loop become large, the performance degrades in a decent way. Since adaptive control is motivated by parameter uncertainties in numerous areas, challenges which combine both parameter uncertainties and input constraints occur. Recently a methodology named “adaptive scaling[10]”was taken into account and the most typical one is “positiveμ-mod[11]”, the main idea of which is to modify tracking error and reference model input constraints to remove the effect of input constraints mostly. Furthermore composite nonlinear control with state and measurement for general multivariable systems with input saturation was presented, in which a design procedure of composite nonlinear feedback(CNF) control for general multivariable with saturation was considered and the control didn’t need impose restrictive assumption on the system’s dynamics[12].
To diminish the effects of input constraints, the control design forsaturated systems must be modified, based on which, a class of problems of input constraints as well as parametric uncertainties is the objective to be solved.
In this technical note, the highlights of the design are as follows:
① It combines CMRAC andμ-mod seamlessly for the stable tracking object and uses BGF for fast convergence, which consequently arrives at a simple structure with a fast and stable performance.
② It just switches to modified part when the adaptive control touches the set virtual limit, while the control is in the reasonable range, modification for the input constraints is not available, thus energy and time will be saved, which is critical in reality, especially in the war or accident.
③ It illustrates the effectiveness of the designed scheme through asimplified longitudinal dynamics of an aerial vehicle like F-16 aircraft.
The paper is organized as follows. In Section 1, the control problem statement and objective are introduced, where a basic MRAC design is also discussed. The adaptive controller structure based on CMRAC and positiveμ-mod is given in Section 2, moreover BGF is also embedded to facilitate fast convergence for parameters during adaptation. In Section 3,the stability of the closed-loop was analyzed, along with the adaptive scheme to update the controller parameters. Section 4 demonstrates the validity of the overall adaptive control scheme by a control application in the F-16 longitudinal dynamics simulation.
1 Model definition
First of all, we put forward a class of single-input (SI) linear time-invariant (LTI) systems as:
(1)

(2)
The objective of the control is to design the input u to make all signals in the closed-loop system bounded and the outputyasymptotically track the command r∈R along with the presence of matched parametric uncertainties {AP,Λ,Θd}.
The system output tracking error is calculated as
ey=y-r
(3)
And we make integrated output tracking error as
(4)
Then we can augment the system to obtain the extended open-loop dynamics.
(5)

As a conclusion, the uncertain systems have an unknown constant matrix A∈Rn×n; known matrices B∈Rn, Bc∈Rn, C∈Rn×m; an unknown positive constantΛ∈Rand an unknown matrix of constant parametersΘd∈RN. The state-dependent regressor vectorΦd(xp)∈RNis assumed to be known. Thus the target of control becomes asymptotically tracking an time-varying command signal r∈R, by the system output y∈Rm, along with the presences of matched parametric uncertainties {A,Λ,Θd} and input constraints given in Eq.(2).
Assumption:
(A,B) is controllable and (A,C) is observable with A∈Rn×n, B∈Rn, C∈Rn×m, andm From the assumption above, we can find that the design purpose only needs to satisfy the basic condition for the plant dynamics. The reference Hurwitz matrix Amis presented as (6) Therefore, the reference model can be obtained as (7) (8) Andletthesystemtrackingerrorhavetheformas e=x-xm (9) Then the adaptive control input is written as (10) It easily results in the tracking error dynamics (11) The adaptive law is given by in the form[1,7] (12) (13) The stability of this system can be found in adaptive control[1, 13]. In this section, several modifications to the basic MRAC approach are made to deal with the problem of input constraints and make the performance smoother and faster. 2.1 Composite model reference adaptive control (CMRAC) A composite MRAC structure[7]was developed by combining two aspects of direct and indirect adaptive control and has been testified with a smooth transient performance. Now the indirect adaptive part will be constructed for that objective. According to the dynamics, we rewrite the extended open-loop system in the form (14) (15) whereλf>0 is a filter inverse constant. For this point forward, the subscript f on a signal denotes a version of that signal that has been filtered byG(s). We filter both sides in Eq.(14) and assume the initial conditions for the filter dynamics are zero. From Eq.(14) we can get λf(x-xf)-Amx-Bcrf=BΛ(uf+ΘTΦf) (16) Then assuming that the rank of B is full, (BTB)-1BT(λf(x-xf)-Amx-Bcrf)= Λ(uf+ΘTΦf) (17) Y=Λ(uf+ΘTΦf) (18) Therefore we can estimate Y according to the bilinear predictor model as the form with (19) The predictor output estimation error is then given by (20) Owning to Eqs.(16)-(20), (21) (22) SincethefundamentalideaofCMRACistocombinedirectMRACwithindirectadaptation,tillnowwecangettheCMRACadaptivelawjustbyaddingtwopartstogether. 2.2Bounded-gainforgetting(BGF) Time-varyingadaptivegainsfacilitatefasterconvergenceofparameterestimatesaswellasdevelopednoisesensitivity.Particularly,theBGF[8]gainadjustmenthasbeenprovedtohaveafastandsmoothconvergenceofparameterestimation.Theadaptivegainadjustmentisselectedas (23) Inwhichρis a positive scalar forgetting factor chosen as (24) whereρ0is the positive constant maximum forgetting rate andkρ0is the positive constant bound on the adaptive gain matrix magnitude. The inverse gain adjustment law in Eq.(23) has several important properties[8]. First, it ensures thatΓΘfto be positively definite. Second, the data forgetting property enables parameter tracking, and is only activated whenΦfilispersistently exciting. Avoiding taking inverses and simplifying implementation, Eq.(23) is replaced by using the equivalent gain adjustment law (25) 2.3Positiveμ-modification Aboveall,abasicmethodispresentedwithoutinputconstraintsandnowwewillmakesomeimprovementsonthatwith“positiveμ-modification[11]”, an application of the idea called“adaptive scaling[10]”. The adaptive scheme with positiveμ-modification can be defined as uc=uad+μΔuc, (26) (27) Werewritethesystemandgettheclosed-loopsystemdynamics: (28) where Δuad=u-uaddenotes the deficiency of the control signal during adaptation. Next we should consider to modify reference model dynamics with the system dynamics (29) Let e=x-xmbe the tracking error signal. Then (30) (31) where ru>0 is corresponding rate of adaptation. And PT>0 solves the algebraic Lyapunov equationas same as Eq.(13). (32) Remark maximum amplitude of the reference signalrmaxis chosen as (33) (34) IfthesysteminitialconditionandtheinitialvalueoftheLyapunovfunctioninEq.(13)satisfy (35) Proof can be referred to the work in Ref.[11]. In this section, we merge CMRAC with BGF and μ-modadaptation, thus create our CBμ-mod model reference adaptive control architecture. The whole adaptive law is formulated as (36) Toaccesstheclosed-loopsystemstability,theLyapunovfunctioncandidateisdefinedas: (37) Then the time derivative of the Lyapunov function is (38) It is known that aTb=trace(bTa), as the trace identity, is also valid for two co-dimensional vector a and b. The time derivative of the Lyapunov function along the system trajectories (36) is (39) (40) 4.1 Aircraft dynamic In this part, it verifies the effectiveness of the methods with stable and smoothing performance of the developed adaptive scheme by simulations. The simulated model used is an F-16 longitudinal dynamics model in a short period as (41) wherexp=[α;q];αis the aircraft angle during attack in radians,qis the pitch rate in radians/second,u=δeis the elevator deflection (control input)in degrees. It is shown that the correspond numerical values of above aerodynamic derivatives in Refs.[7, 14]. All particular values are set for an F-16 aircraft trimmed on the assumption of sea level as 4.2 Parameters setting The control objectives tracking a time-varying whereas bounded angle of commandr=αcmdwith a variety of uncertainties. Moreover let Q=diag[0.1, 1, 800] tosolve the Lyapunov function to getP. Furthermore, rates of adaptation areΓΘ=diag[1, 100, 100, 20],ΓΛ=8. The filterinverse constant and the CMRAC gain are set asλf=10,rc=10. For BGF,ρ0=0.9 andkρ0=100. 4.3 Simulation results and analysis To testify the effective of the adaptive controller, we set two different conditions with different parameters as follows: ① Composite adaptive control without input constraints. ② Composite BGFμ-mod model reference adaptive control with input constraints. In this case, we set the positiveμ-mod parameters asumax=1.5,δ=0.2umax,μ-5,ru=0.4. Example 1: In this case, we assume parameters are unknown without input constraints. Signals for the input are given as squares. Simulation results are shown in Fig.1. Design based on CMRAC indeed results in improved performance. Fig.1 Case 1: results of CMRAC in the presence of parametric uncertainties without input constraints Fig.2 Case 2: results of composite BGF μ-mod in the presence of parametric uncertainties and input constraints By combining several modifications to a basic MRAC, we derive a new and effective architecture to solve the problem of uncertainties and input constraints. Not only the goal of asymptotic tracking performance is attained, but also fast convergence for adapted parameters is obtained. The availability of these modifications motivates a fresh perspective for further studies. For different purposes, corresponding methods can be adopted and analyzed. Consequently an overall scheme can be conceived. Furthermore simulation results on a flight vehicle indicate the validity of the whole design structure. The future work contains analysis about details of research for input constraints. [1] Narendra K, Annaswamy A. Stable adaptive systems[M]. North Chelmsford, MA: Courier Corporation, 2012. [2] Narendra K S, Annaswamy A M. Robust adaptive control[C]∥American Control Conference, 1984: 333-335. [3] Tao G. Adaptive control design and analysis[M]. New York: John Wiley & Sons, 2003. [4] Ioannou P A, Sun J. Robust adaptive control[M]. Mineola: Dover Publications, 2012. [5] Lavretsky E, Wise K A. Robust and adaptive control: with aerospace applications[M]. Berlin: Science & Business Media Springer, 2013. [6] Sastry S, Bodson M. Adaptive control: stability, convergence and robustness[M]. North Chelmsford, MA: Courier Corporation, 2011. [7] Lavretsky E. Combined/composite model reference adaptive control[J]. Automatic Control, IEEE Transactions on, 2009, 54(11): 2692-2697. [8] Slotine J J E, Li W. Applied nonlinear control[M]. Upper Saddle River, New Jersey: Prentice Hall, 1991. [9] Morabito F, Teel A R, Zaccarian L. Nonlinear antiwindup applied to Euler-Lagrange systems[J]. Robotics and Automation, IEEE Transactions on, 2004, 20(3): 526-537. [10] Monopoli R V. Adaptive control for systems with hard saturation[C]∥Decision and Control Including the 14th Symposium on Adaptive Processes, 1975 IEEE Conference on, 1975, 14: 841-843. [11] Lavretsky E, Hovakimyan N. Stable adaptation in the presence of input constraints[J]. Systems & Control Letters, 2007, 56(11): 722-729. [12] He Y, Chen B M, Wu C. Composite nonlinear control with state and measurement feedback for general multivariable systems with input saturation[J]. Systems & Control Letters, 2005, 54(5): 455-469. [13] Khalil H K. Nonlinear systems[M]. Upper Saddle River, New Jersey: Prentice Hall, 2002. [14] Stevens B L, Lewis F L. Aircraft control and simulation[M]. New York: John Wiley & Sons, 2003. (Edited by Wang Yuxia) 10.15918/j.jbit1004-0579.201524.0319 TP 273.2 Document code: A Article ID: 1004- 0579(2015)03- 0405- 08 Received 2013- 12- 24 Supported by Deep Exploration Technology and Experimentation Project (201311194-04) E-mail: wuwb296@126.com
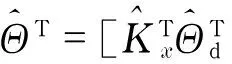
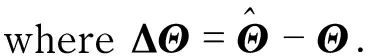

2 Modifications to MRAC approach




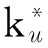

3 Stability analysis

4 Simulation example



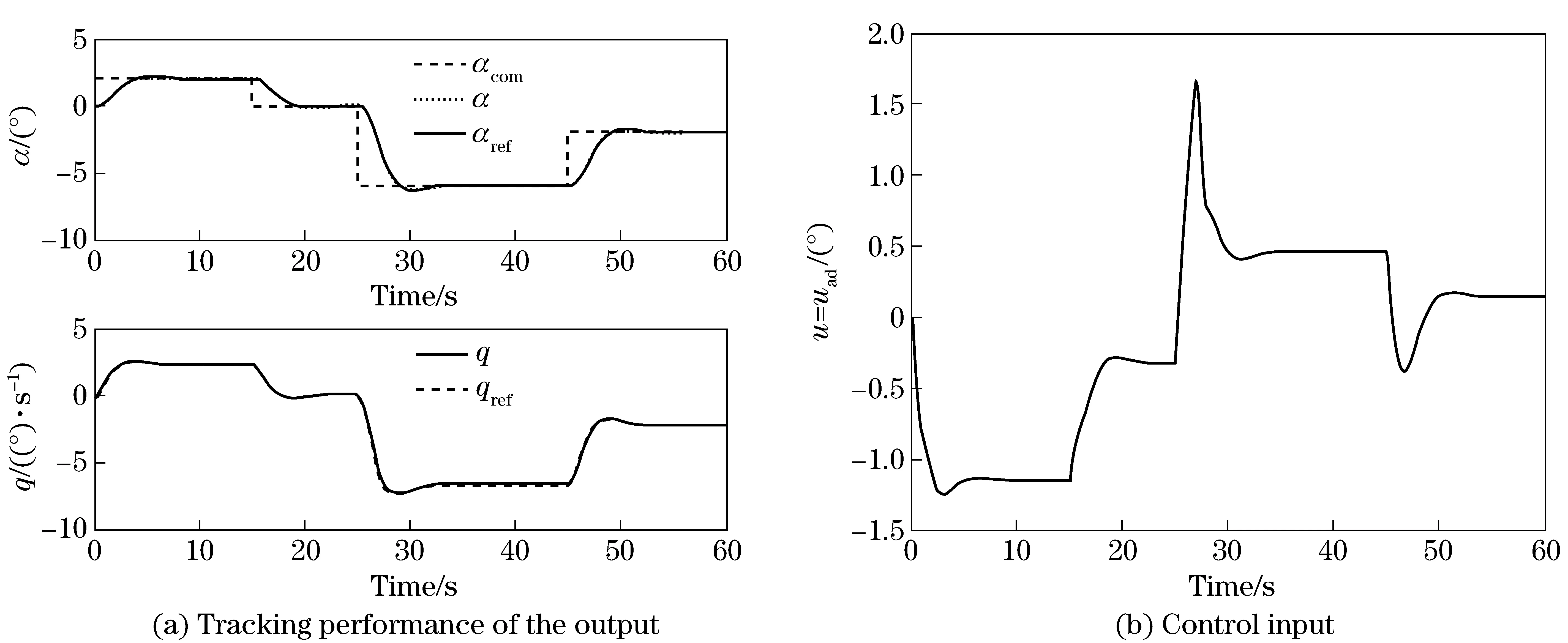


5 Conclusion
杂志排行
Journal of Beijing Institute of Technology的其它文章
- Anti-hypertensive effects of rosiglitazone on renovascular hypertensive rats: role of oxidative stress and lipid metabolism
- On a novel non-smooth output feedback controller for the attitude control of a small float satellite antenna
- Facial expression recognition with contextualized histograms
- Length estimation of extended targets based on bistatic high resolution range profile
- Joint receiving mechanism based on blind equalization with variable step size for M-QAM modulation
- Coherence-based performance analysis of the generalized orthogonal matching pursuit algorithm
