探空火箭通信系统最优信噪比切换阈值的设计
2015-04-22熊蔚明于世强陈志敏
陈 萍, 熊蔚明,于世强,陈志敏
(1.中国科学院空间科学与应用研究中心,北京 100190;2.中国科学院大学,北京 100049;3.中国船舶工业系统工程研究院,北京 100036;4.中国空间技术研究院载人航天总体部,北京 100094)
探空火箭通信系统最优信噪比切换阈值的设计
陈 萍1,2,3, 熊蔚明1,于世强4,陈志敏1
(1.中国科学院空间科学与应用研究中心,北京 100190;2.中国科学院大学,北京 100049;3.中国船舶工业系统工程研究院,北京 100036;4.中国空间技术研究院载人航天总体部,北京 100094)
结合Nakagami衰落信道模型,分析了探空火箭飞行过程中经历的瑞利信道和莱斯信道的特性,以BPSK、QPSK、16QAM、64QAM 4种调制方式结合的可变调制传输系统为例,提出了可根据地面数据接收站天线的不同仰角,计算最优信噪比切换阈值的方法。最优信噪比切换阈值在满足误码率指标的前提下,使系统的数据吞吐量最大。进一步比较了采用最优信噪比阈值与采用BPSK固定调制方式、恒定误码率信噪比阈值的吞吐量差异,结果表明,采用最优信噪比阈值法得到的数据平均吞吐量分别是另外2种方法的3.89倍和1.043倍。其结果为可变调制技术在探空火箭工程中的应用提供参考依据。
可变调制;最优信噪比阈值;探空火箭
0 引言
探空火箭在飞行过程中,与地面数据接收站的距离不断变化,传统的固定调制模式的通信系统只能依据最差的信道条件来设计,在信道条件好的时候不能充分利用信道容量。可变调制系统可根据无线信道的时变特性,动态改变自己的信号发射参数,包括符号率、编码率、编码方式等,从而在给定数据传输质量要求的前提下,充分利用信道容量,提高有效载荷的数据吞吐量。在探空火箭中应用可变调制技术,根据不同的信道条件选择不同的调制方式,能够在不改变系统发射及接收能力、满足目标误码率的前提下,提高系统吞吐量,是未来提高探空火箭对地数据传输能力的关键技术之一。
许多学者对可变调制技术进行了深入的研究。早在1968年,Hayes提出了根据接收端反馈的信道信息进行可变调制传输[1]的方法,这是最早提出的根据信道状态进行可变调制传输的思想。Webb 和Steel 最先研究了在加性白色高斯噪声(AWGN)信道条件下正交幅度调制方式(QAM)满足误码率(BER)指标时的信噪比[2]。Torrance和Hanzo研究了在系统平均BER的限制下,可变调制方式的BER性能上界和对应的自适应调制系统的数据吞吐量性能[3],提出基于当前信道衰落和系统BER要求来选择合适的调制方式。另外还综合考虑误码率BER代价和吞吐量BPS代价,使其综合加权代价最小而获得最佳切换门限值[4]。Choi和Hanzo采用拉格朗日乘数法得到了在单径瑞利信道模型下自适应正交幅度调制(AQAM)系统的最佳切换门限值[5-6],还将所得结果与加权法所得的最佳门限值作了比较,结果表明采用拉格朗日乘数法得的最佳信噪比切换门限值使AQAM系统的平均吞吐量性能更好。但文献[5-6]没有针对火箭或移动卫星信道提出分析方法。文献[7]采用ITU-R M.1225中定义的Vehicular Test模型,研究了在该信道模型下自适应调制系统的最佳信噪比门限值,该模型可近似高速移动环境下多径瑞利衰落信道,但与探空火箭的通信信道有明显不同。
回顾最优信噪比切换阈值的研究进展,不难发现,最优信噪比切换阈值的计算一般基于理论模型,而对于火箭或者移动卫星,尚未有最优信噪比门限值计算的相关文献。目前采用的普遍方法是将传输信道近似为AWGN模型,计算AWGN信道模型下每种调制方式满足BER指标时的信噪比。该方法可保证系统采用各调制方式时都能满足预定BER指标,是一种局部最优的方法,但是该方法不能使系统整体的吞吐量最大化,不是全局最优的方法。此外,AWGN信道模型是一种理论模型,与探空火箭的信道模型也存在较大差异。
本文采用全局最优的思路,结合Nakagami信道模型,分析了探空火箭在飞行过程中火箭与地面通信经历的瑞利信道、莱斯信道特性,以BPSK、QPSK、16QAM和64QAM 4种调制方式结合的可变调制系统为例,提出了探空火箭最优信噪比切换阈值的计算方法,该方法使系统的吞吐量最大,同时保证系统的误码率达到任务指标的要求。
1 通信信道与接收天线仰角的关系
探空火箭飞行过程中,火箭与地面通信的信道特性较为复杂,目前尚无成熟的理论分析。通过借鉴有关文献对卫星信道的分析[8],认为通信信号因受建筑物、透明体和障碍物等散射、折射和反射的影响,地面遥测接收站接收到的信号是不同强度和相位、不同延迟时间的多径传播信号的叠加。在没有直视分量的情况下,信号的统计特性可以用瑞利(Rayleigh)分布来描述。如果在宽阔地域良好通信环境下,信号中存在直视分量信号,信道特性用莱斯(Rician)分布描述。
为了更好描述信道特性,本文使用了Nakagami衰落信道模型作为仿真模型[9]。该模型也称为广义信道模型,由日本著名学者Nakagami 20世纪60年代提出,通过现场测试并用曲线拟合的方法来描述信道,以寻求近似分布。由于Nakagami分布是基于曲线拟合方法得到的,因此它并没有相应的物理模型。但是根据该分布的表达形式,可理解为它是由几组多径波组合而成的分布,在任何一组多径波组合内,散射波的相位是随机的但具有相近的时延,而在不同组内,时延差别比较大。平坦Nakagami信道中,信噪比γ的概率密度函数p(γ)表示为
(1)
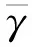
m表示信道衰落的严重程度,m越小衰落越严重,m越大衰落越不明显。当m=1时,模型为瑞利衰落信道模型;当m>1时为莱斯信道模型。通过调整参数m的值,Nakagami模型能够逼近严重、适中、轻微到无衰落的信道特性。
利用高度为350 km的探空火箭弹道数据,计算得到其在飞行全过程中地面数据接收站天线的仰角变化如图1所示,接收站天线的仰角变化范围为0°~82°。
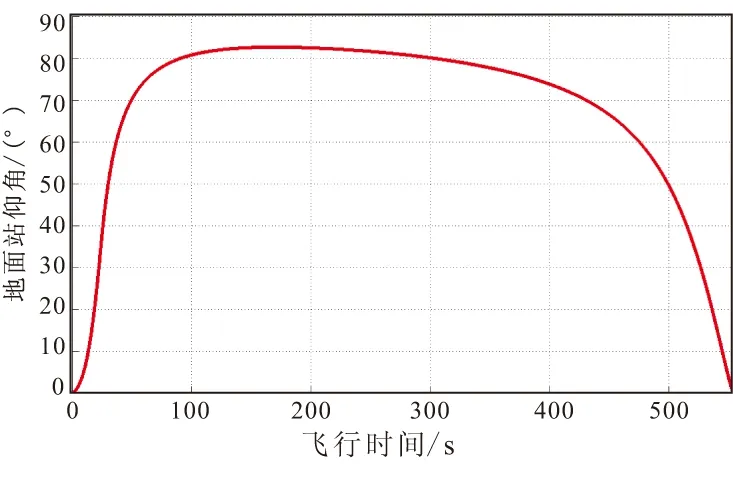
图1 地面数据接收站天线仰角的变化Fig.1 Change of elevation angles of ground data receiving station
当地面站天线仰角小于5°,通信信道受地形地貌等因素的影响明显,多径分量强而直视分量很弱或不存在,信道可用瑞利信道近似,相当于Nakagami信道模型参数m=1。当地面站天线仰角大于5°,除直视分量外会出现较多的多径分量,信道用莱斯信道近似,相当于Nakagami信道模型参数m>1。信道类型与天线仰角之间的关系如图2所示。
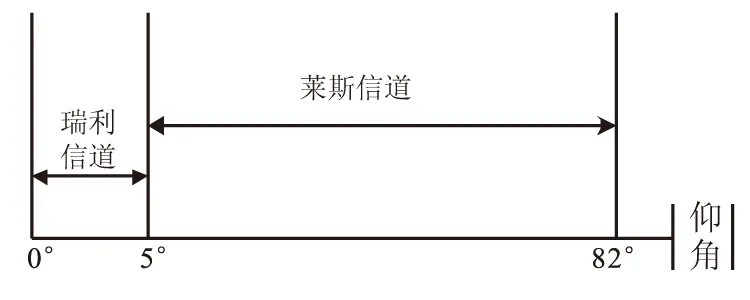
图2 地面数据接收站天线仰角的变化Fig.2 Relationship between channel types and elevation angles
为了表征莱斯信道下直射分量与多径分量的相对大小,引入了莱斯因子K[10],其定义如式(2)所示:
(2)
式中S2为直视分量的功率;σ2为被散射多径分量的实部或虚部的均值功率。
实际卫星链路特性的测试结果表明[11-12],在树木遮蔽条件下,莱斯信道的莱斯因子K与遥测接收站天线仰角α之间的经验式为
K(α)=K0+K1(α)+K2α2
(3)
其中,K0=2.73,K1=-0.10 74,K2=0.002 774。
莱斯因子K与Nakagami模型衰落因子m之间有一一对应关系[13-14]:
(4)
根据式(3)和式(4),可由地面站天线仰角的不同得到信道衰落因子m的近似值。进一步,由式(1)可知,m因子一定的情况下,还可得到不同平均信噪比条件下对应的信道信噪比的概率密度函数,而概率密度函数是Nakagami信道条件下信噪比切换阈值确定的重要依据。
2 探空火箭可变调制系统
探空火箭可变调制系统设计为根据不同的信道条件,采用不同的信号调制方式。设探空火箭采用k种调制方式组合的调制系统,根据接收端测量的信道质量ξ来选择相应的调制方式。选择第k∈{0,1,…,K-1}种调制方式的准则为
sk≤ξ≤sk+1
(5)
信道质量ξ是瞬时信道信噪比,也可是瞬时每符号信噪比。本文设ξ代表瞬时信道信噪比。信噪比切换阈值sk属于:
(6)
通常设so=0,sK=∞。用bk表示各种调制方式下每符号比特数,mk表示各种调制方式的阶数,则bk=log2(mk),定义ck=bk-bk-1,且有c0=b0。假设探空火箭的可变调制系统设计了BPSK、QPSK、16QAM和64QAM 4种调制方式进行组合传输,调制方式的参数如表1所示,其中No-Tx表示不进行传输。
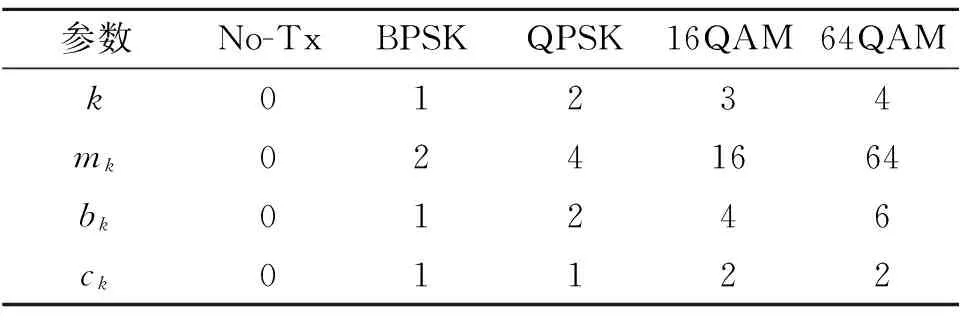
表1 不同调制模式的系统参数Table1 System parameters of different modulation modes
3 最优信噪比切换阈值的计算方法
最优信噪比切换阈值的计算方法参考文献[5]利用拉格朗日(Lagrange)乘数法计算最大极值的思路。设系统的平均吞吐量为B,单位为比特/符号(bit/symbol)。已知信噪比概率密度p(λ)的表达式如式(1)所示,则平均吞吐量可表达为
(7)
设第k种调制方式在AWGN信道下的误码率为pmk,则在Nakagami信道条件下每种调制方式的误码率可表达为
(8)
对PSK调制和QAM调制方式的误码率表达式为
(9)
对应于BPSK、QPSK、16QAM和64QAM调制的参数{Ai,ai}参见文献[5]。
设4种调制方式组合情况下的系统平均误码率为Pavg,则表达式为
(10)
设预定的误码率指标为Pth,要得到最佳信噪比切换阈值,就要使得系统平均吞吐量B在满足约束条件Pavg=Pth的情况下取得最大。故有:
(11)
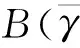
(12)
根据拉格朗日乘数法,最优信噪比切换门限s应满足:
(13)
对式(13)中的(a)展开,得到:
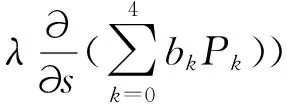
(14)

(15)
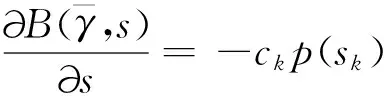
(16)
把式(15)、式(16)代入式(14)得到:
[ck(1-λPth)-λ{bk-1pmk-1(sk)-bkpmk(sk)}]p(sk)=0
(17)
式(17)的一个解是p(sk)=0,但不是问题的解,所以有
ck(1-λPth)-λ{bk-1pmk-1(sk)-bkpmk(sk)}=0
(18)
对式(18)进行等式变形,得到:
(19)
由于式(18)等式左边为定值,可知对于k∈{1,…,K-1}都有如下关系成立:
(20)
由式(20)可知,最佳门限值sk与s1之间的关系是确定的,与信号功率和信道状态无关,已知s1可确定sk,反之亦然。
进一步地,将约束条件式(11)展开,得到:

(21)
对式(21)进行整理,得到:
(22)

综上所述,计算探空火箭最优信噪比切换阈值的方法可以总结为图3所示的步骤,得到的结果即为接收站不同仰角条件下的最优信噪比切换阈值。

图3 计算探空火箭最优信噪比切换阈值的步骤Fig.3 Method of Computing the optimum signal-to-noise ratio switch threshold
4 数值分析
下面仍以高度为350 km的探空火箭弹道数据为例,计算最优信噪比切换阈值。根据式(3)和式(4)确定衰落因子m的计算方法,取接收天线仰角为以下典型值时,计算对应的信道衰落因子m,结果见表2。

表2 接收天线仰角与m的对应关系Table2 Relationship between elevation angles and m value
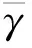
在误码率为10-6条件下,瑞利信道以及衰落因子m=2.2、6.3的莱斯信道条件下的信噪比最优切换阈值如图4所示。在平均信噪比分别为0、5、10、15、20、25、30、35 dB的情况下,计算出对应于BPSK、QPSK、16QAM、64QAM这4种调制方式的最优信噪比切换阈值,用曲线将仿真的数值点连接起来,得到最优信噪比切换阈值与系统平均信噪比之间的关系,图中S1、S2、S3、S4分别表示采用BPSK、QPSK、16QAM和64QAM调制方式的最优切换阈值。
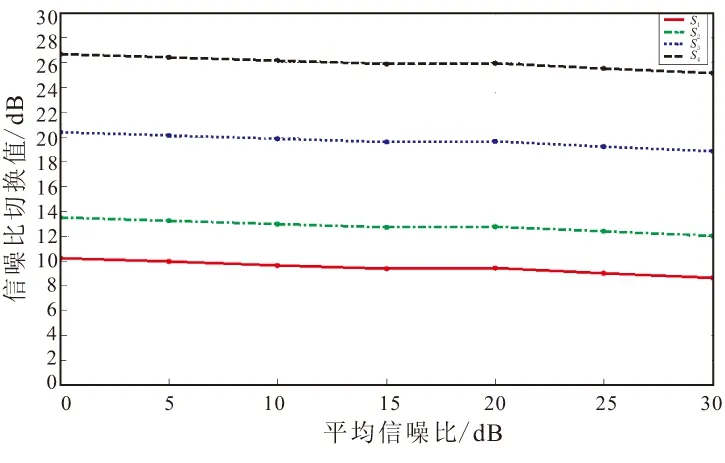
(a)m=1
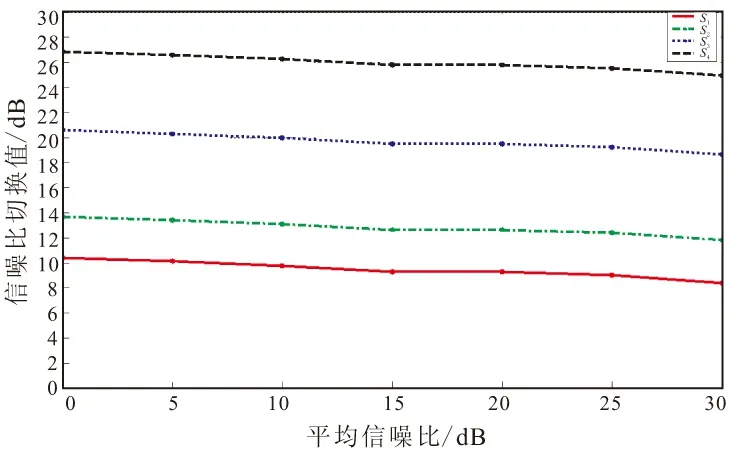
(b)m=2.2
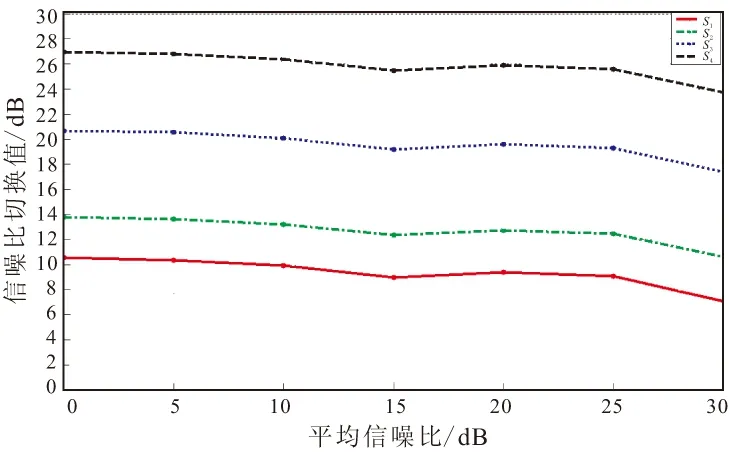
(c)m=6.3
由图4可见,当误码率一定时,随着系统平均信噪比的增加,最优切换阈值总体趋势是逐渐减小。这是因为在信道状态不变的情况下平均信噪比增加,表明信号发送功率有所增加,采用较高阶的调制方式仍可满足误码率要求。探空火箭飞行过程中火箭与地面通信经历的信道模型涵盖了瑞利信道及莱斯信道的多种情况,信噪比最优切换阈值也需要结合飞行参数及不同信道模型得到。其中,平均信噪比的值与火箭飞行的弹道关系密切,不同的径向通信距离对应不同的平均信噪比。经过计算,当天线仰角分别为0°~5°; 5°~40°;40°~66°; 66°~78°; 78°~82°时,地面站收到信号的平均信噪比分别为29,28,25,19、11 dB。结合不同信道模型下最优切换阈值,采用图3所示的方法,可得到表3所示的最优信噪比切换阈值(分别对应于BPSK、QPSK、16QAM、64QAM)。

表3 不同天线仰角对应不同的m值和平均信噪比Table3 relationship of elevation angles and m values and average SNR per symbol
由前述可知,最优信噪比切换阈值是保证系统满足误码率指标要求下,保证系统最大吞吐量的信噪比切换值,是基于系统整体最优的方法得到的结果。为了比较最优噪比切换阈值对系统吞吐量的提高,分别采用最优信噪比切换阈值和恒定误码率信噪比切换阈值两种方法计算系统吞吐量,且计算时均采用同样的探空火箭弹道数据模型。恒定误码率信噪比切换阈值依据AWGN信道下不同调制方式的误码率曲线得到,误码率为10-6时信噪比切换阈值见表4,平均吞吐量3.73 bit/symbol。采用最优信噪比切换阈值得到的平均吞吐量3.89 bit/symbol。如果原有固定调制方式为BPSK,平均吞吐量1 bit/symbol,则用最优信噪比切换阈值获得的吞吐量是固定调制方式的3.89倍,是恒定误码率信噪比切换方法的1.043倍,提升了4.3%。

表4 恒定误码率信噪比切换阈值Table4 Constant BER SNR switch threshold dB
5 结论
(1)探空火箭信道模型不能简单近似为AWGN信道模型,因为地面接收站收到的信号是不同强度和相位、不同延迟时间的多径传播信号的叠加。因此,探空火箭信道模型可用Nakagami信道模型进行分析。
(2)采用拉格朗日乘数法得到的最优信噪比切换阈值,可在保证系统误码率达到指标要求的前提下,使系统平均吞吐量达到最大,该方法是一种系统全局最优的方法。
(3)在探空火箭的对地通信系统中,需要紧密结合地面接收站天线的仰角进行具体分析,根据接收站仰角对接收范围进行分段,计算不同仰角的各段对应的最优信噪比,是一种针对探空火箭可变调制系统的具体工程计算方法。
[1] Hayes J F.Adaptive feedback communications[J].IEEE Transactions on Communications,1968,16(1):29-34.
[2] Webb W T,Steele R.Variable rate QAM for mobile radio[J].IEEE Transactions on Communications,1995,43(7):2223-2230.
[3] Torrance J M,Hanzo L.Upper bound performance of adaptive modulation in a slow Rayleigh fading channel[J].Electronics Letters,1996,32:218-719.
[4] Torrance J M,Hanzo L.Optimization of switching levels for adaptive modulation in a slow Rayleigh fading[J].Electronics Letters,1996,32:1167-1169.
[5] Choi B J,Hanzo L.Optimum mode-switching assisted constant-power single- and multicarrier adaptive modulation[J].Vehicular Technology,2003,52(3),:539-541.
[6] Choi B J,Hanzo L.Optimum mode-switching assisted adaptive modulation[C]//Global Telecommunications Conference.2001 GLOBECOM'01, 2001,6:3316-3320.
[7] 高欢芹,酆广增,朱琦.AQAM 系统最佳信噪比门限值的研究及其在IEEE802116e中的应用[J].电子学报,2009,37(7):1465-1469.
[8] 杨友福,张其善,刘建伟.移动卫星信道建模与统计分析平[J].遥测遥控,2009,30(6):30-34.
[9] Clarker H.A statistical theory of mobile-radio reception[J].Bell.Syst.Tech.,1968,47(6):957-1000.
[10] (挪)裴措特,著,王秋爽,译.移动无线信道(第二版)[M].机械工业出版社,2014.
[11] 吴诗其,吴廷勇,卓永宁.卫星通信导论[M].电子工业出版社,2006.
[12] 吴诗其,朱立冬.通信系统概论[M].清华大学出版社,2005:84.
[13] 吴志中.移动通信无线电波传播[M].人民邮电出版社,2002.
[14] GoldSmith A.Wirelss communication[M].Cambridge University Press,2005.
(编辑:薛永利)
Design of the optimum signal-to-noise ratio switch threshold of sounding socket communication system
CHEN Ping1,2,3, XIONG Wei-ming1,YU Shi-qiang4,CHEN Zhi-min1
(1.Center for Space Science and Applied Research of Chinese Academy of Sciences, Beijing 100190,China;2.Graduate University of Chinese Academy of Sciences ,Beijing 100049,China;3.Engineering Research Institute of China State Shipbuilding Corporation System,Beijing 100036,China;4.Institute of Manned Space System, China Academy of Space Technology,Beijing 100094,China)
Combining with Nakagami fading channel model,Rayleigh channels and Rician channels were analyzed between sounding rockets and ground station during the flight course.It takes an example of a variable modulation system with four types of modulations,including BPSK,QPSK,16QAM and 64QAM,and proposes a method to acquire the optimum signal-to-noise ratio switch threshold,according to different elevation angles of ground receiving station.The optimum threshold could maximize the throughput,while satisfying BER goal.Furthermore, the paper analyzes and compares the throughput difference with optimum signal-to-noise ratio switch threshold,BPSK modulation method and constant-BER signal-to noise ratio threshold. The results show that,by adoption of the optimum threshold,system throughput is 3.89 times and 1.043 times higher than the other two methods,respectively.The results could provide reference and basis for the application of variable modulation technology into practical sounding rockets projects.
variable modulation;optimum signal-to-noise ratio threshold;sounding rocket
2014-05-17;
:2014-07-18。
国家863项目(2011AA7033045)。
陈萍(1983—),女,博士生,研究方向为空间无线通信技术。E-mail:chen_elppa@163.com
V556
A
1006-2793(2015)04-0595-06
10.7673/j.issn.1006-2793.2015.04.027
