小型柔性接头力矩特性数值与试验研究
2015-04-22杨敬贤任军学郝文强曹熙伟
杨敬贤,王 超,任军学,刘 宇,郝文强,曹熙伟
(1.上海新力动力设备研究所,上海 200125;2.北京航空航天大学 宇航学院,北京 100191;3.中国运载火箭技术研究院研究发展中心,北京 100076)
小型柔性接头力矩特性数值与试验研究
杨敬贤1,王 超2,任军学2,刘 宇2,郝文强2,曹熙伟3
(1.上海新力动力设备研究所,上海 200125;2.北京航空航天大学 宇航学院,北京 100191;3.中国运载火箭技术研究院研究发展中心,北京 100076)
为了研究柔性接头在固定燃烧室压强下的各个力矩特性,设计了弹性件材料为硅橡胶的小型柔性接头,测试了一系列9 MPa燃烧室压强条件下接头在正弦激励下的动态特性,获得不同振幅、不同频率正弦激励下柔性接头的摆角力矩曲线,根据接头在0°摆角的力矩获得摩擦力矩,根据摆角力矩曲线的近线性部分获得弹性比力矩,通过最大角度差和力矩差获得总比力矩,在此基础上研究了摆动频率和振幅对各个力矩的影响。结果表明,库仑摩擦力矩随着振幅增大而增大,粘滞摩擦力矩随着摆动速度的增大而增大,弹性比力矩随着振幅的增大先减小后增大,随着摆动频率的增大而增大,总比力矩随着振幅的增大先减小后增大,随着频率的增大而增大。
柔性接头;推力矢量控制;摩擦力矩;弹性比力矩;总比力矩
0 引言
柔性接头是由前法兰、后法兰、增强件和弹性件4部分组成的推力矢量控制执行部件。增强件和弹性件一般为多层且交替粘接而成。一般用在大型战略弹和助推器上。近年来,随着战术导弹对垂直发射快速转弯、越肩发射等机动性要求的提高,柔性接头以其结构简单、冲质比高、推力损失小等优点受到各国的青睐[1-4],美国的SM-3和Terrier LEAP的第二级发动机,欧洲的aster15/30助推器等都采用了柔性接头作为其推力矢量控制方式[5-8]。
柔性接头的力矩可分为弹性比力矩、摩擦力矩、偏位力矩、惯性力矩和气动力矩等。其中,弹性比力矩和摩擦力矩占主要部分[9],而摩擦力矩又分为库仑摩擦力矩和粘滞摩擦力矩。目前,国内外对柔性接头的力矩分离都进行了大量研究,国内刘志武、杨世学等都将柔性接头看成变阻尼的质量弹簧系统[10-11],认为在一定燃烧室压强下,随着激振频率增加,柔性接头摩擦力矩增加,弹性比力矩保持不变,忽略了激振频率对弹性比力矩的影响,也未考虑激振振幅对弹性比力矩和摩擦力矩的影响。文献[12]虽然指出库仑摩擦力矩受振幅和燃烧室压强的影响很大,但并未研究其变化规律,对其内在原因也未进行详细分析。
本文开展了一系列硅橡胶弹性件小型柔性接头在9 MPa燃烧室压强下的动态特性试验,测试了柔性接头在不同频率、不同振幅正弦波激振条件下的摆角力矩特性,研究了接头弹性比力矩、粘滞摩擦力矩及库仑摩擦力矩随摆动频率和振幅的变化规律,研究结果可为柔性接头动态精确建模、时域响应分析和传递函数的建立提供依据。
1 柔性接头及试验系统
1.1 柔性接头
柔性接头的结构如图1所示,由前法兰、后法兰、防热套、增强件和弹性件组成。主要参数及具体的结构参数如表1所示,弹性件与文献[13]中所提硅橡胶一致。
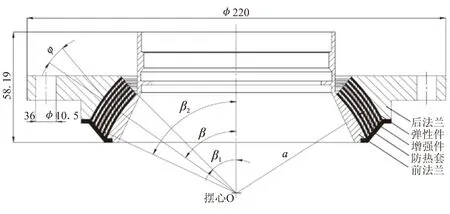
图1 柔性接头Fig.1 Flexible joint

表1 柔性接头结构参数Table 1 Structure parameter of flexible joint
1.2 试验系统
柔性接头冷试试验系统装置如图2所示。在压力容器充填高压氮气模拟燃烧室压强环境,电动伺服机构通过驱动器产生不同振幅、不同频率的正弦激励信号,用于提供柔性接头摆动所需作动力矩。两个水平安装的位移传感器用于测试柔性接头摆角,铅垂安装的位移传感器结合两水平传感器用于测试柔性接头的摆心[9],拉压力传感器用于测试伺服机构所提供的作动力,测得摆心和作动力后,则可按文献[9]中的方法计算出作动力矩。

图2 柔性接头冷试试验系统Fig.2 Cold-flow experiment system for flexible joint
2 力矩辨识方法
图3是柔性接头在一定燃烧室压强、某一振幅和摆动频率下的摆角力矩曲线。
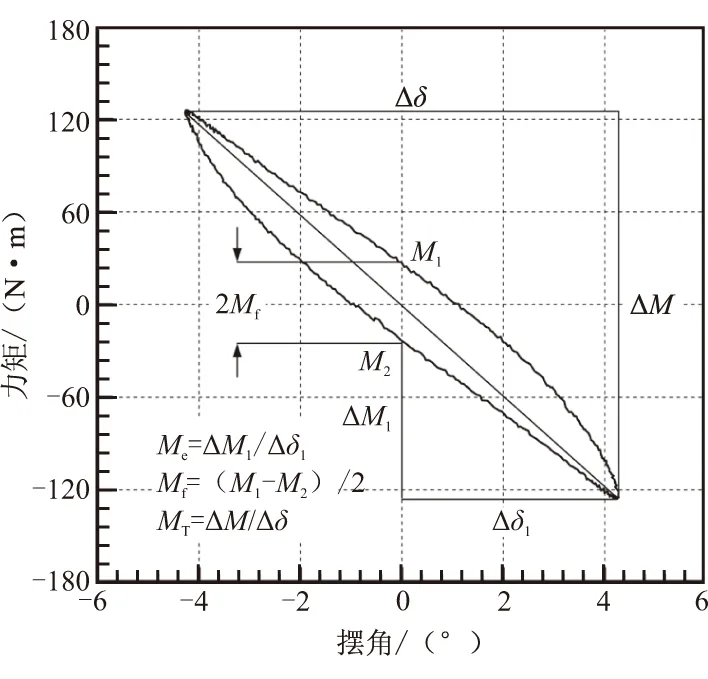
图3 力矩辨识方法Fig.3 Method of torque identification
从图3可看出,摆角力矩曲线呈回环状态,曲线面积即代表着每个周期损耗的能量,曲线上下两部分都有近似线性的部分,且保持平行,说明柔性接头的力矩存在与摆角成比例的弹性部分,在振幅最大处摆动方向变换时,曲线斜率变化较大。这是由于弹性件碳黑填充颗粒的影响,使得柔性接头出现类似库仑摩擦的现象,对于填充类橡胶制品承受循环载荷时,不论加载频率有多低,都会出现这种现象[14]。
因此,低频摆动时,摆角为0°处的力矩近似为库仑摩擦力矩。对于本接头,将0.1 Hz摆动频率时摆角为0处的力矩近似为库仑摩擦力矩,随频率的提高,摆角为0°处的力矩变为库仑摩擦力矩和粘滞摩擦力矩之和,摩擦力矩Mf、弹性比力矩Me和总比力矩MT的定义及计算方法见图3。
3 试验结果及分析
3.1 频率对各力矩的影响
图4是柔性接头在9 MPa容压、3.21°振幅、不同摆动频率下的摆角力矩曲线。从图4可看出,随摆动频率的增大,接头在每个周期载荷内迟滞环围成的面积增大,损耗能增加,阻尼增加;在0°摆角位置的力矩增大,摩擦力矩增大;迟滞曲线发生了转动,柔性接头的弹性比力矩和总比力矩增加,这是由于橡胶材料的粘弹性引起的。图5是摩擦力矩和弹性比力矩随摆动频率的变化曲线。从图5可看出,在0.1~1 Hz范围内,随摆动频率的增大,弹性比力矩、摩擦力矩和总比力矩都呈非线性增大趋势,且增大的速率随摆动频率的增大而减小,弹性比力矩数值从23.8 N·m/(°)增大到26.23 N·m/(°),摩擦力矩的数值从19.63 N·m增大到24.12 N·m,总比力矩从30.09 N·m/(°)增大到33.23 N·m/(°),摩擦力矩占总力矩的比例从21.7%上升到24.2%,按第二章中库仑摩擦力矩计算方法,本柔性接头在9 MPa燃烧室压强和3.21°振幅下柔性接头的库仑摩擦力矩约19.63 N·m。
3.2 振幅对各力矩的影响
图6是柔性接头在9 MPa容压、0.1 Hz摆动频率、不同振幅正弦激励下的摆角力矩曲线,图7是摩擦力矩、弹性比力矩和总比力矩随振幅的变化关系图。从图7可看出,库仑摩擦力矩随振幅的增大基本呈线性增大趋势,弹性比力矩和总比力矩随着振幅的增大先减小、后增大。
库仑摩擦力矩数值由1.1°振幅的8.07 N·m增大到6.28°振幅的33.54 N·m,增大的幅度达到315.6%。可见,在一定燃烧室压强下,振幅对柔性接头的库仑摩擦力矩影响很大,对于固定的柔性接头,库仑摩擦力矩并非固定值,而是在一定的燃烧室压强和振幅下保持不变,在一定的燃烧室压强下,库仑摩擦力矩随着振幅的增大而增大;弹性比力矩和总比力矩随着振幅的增大先减小、后增大,且拐点都在4.31°左右;由于总比力矩是摩擦力矩和弹性比力矩共同作用的结果,因此分析清楚摩擦力矩和弹性比力矩的变化原因即可。

图4 3.21°振幅下不同摆动频率摆角力矩曲线Fig.4 Curves of torque vs vector angle under different swing frequencies at 3.21° excitation amplitude

图5 3.21°振幅下各力矩随频率的变化关系Fig.5 Curves of the relation for each torque with the swing frequency at 3.21° excitation amplitude

图6 0.1 Hz摆动频率、不同振幅迟滞环曲线Fig.6 Hysteresis loops with amplitudes ranging from 1° to 6° at 0.1 Hz swing frequency
Payne在1962年的研究中指出,对于颗粒填充类橡胶,在一定的很小应变范围内,剪切模量保持不变,超过这个应变时,剪切模量会随着应变的增大而下降,这种影响随着应变的增大而减小[15-16],而阻尼则在一定的应变值时达到最大,微观上的解释是由于填充结构和聚合链之间的弱键变化导致的,当橡胶变形时,这些键将沿着填充粒子的表面移动,从而导致频率无关的能量损失。因此,柔性接头的库仑摩擦力矩随着振幅的增大而增大,而弹性比力矩的变化规律则是橡胶的Payne效应和超弹性共同作用的结果,随着振幅的增大先减小,到一定振幅时,Payne效应影响减弱,橡胶的超弹性变化则变为主导因素,导致接头的弹性比力矩上升。从图6中接头6.28°振幅的摆角曲线可看出,在此振幅下,摆角力矩曲线迟滞环的近线性段出现拐点,拐点位置约在4.31°摆角处,这与图7中弹性比力矩的曲线拐点基本一致。图8是柔性接头所用橡胶的简单拉伸和剪切试验数据。从图8可看出,橡胶的剪切模量呈现出先减小、后增大的趋势,其拐点出现在应变ε≈1.5的位置处,基于ANSYS软件计算柔性接头在9 MPa容压、4.31°摆角下弹性件在球坐标系(r,θ,φ)下的剪切应变εrθ。
3.2.1 网格
柔性接头为轴对称体,但由于加载过程中变形及载荷非对称,采用三维有限元模型进行数值模拟,弹性件选择六面体八节点的SOLID185号单元,增强件选择SOLID45号单元,各层弹性件、增强件沿厚度方向划分3等份,沿宽度方向划分20等份,沿圆周方向划分25等份,见图9。球坐标系(r,θ,φ),坐标原点O位于柔性接头几何回转中心(设计摆心),作动器位于φ=0°平面内。

图7 0.1 Hz摆动频率下各力矩随振幅的变化关系Fig.7 Curves of the relation for each torque with the excita-tion amplitude at 0.1 Hz swing frequency
3.2.2 边界条件
对称面φ=0°、180°施加对称边界条件,后法兰上顶面,中顶面、外侧面和防热套的上外侧面设为固定端,压强载荷均匀作用于柔性接头所有和气体接触的湿表面,在前法兰的关键点上施加等效的作动力载荷模拟柔性接头的摆动。
3.2.3 材料属性
柔性接头增强件及前后法兰材料30CrMnSiA为线弹性材料,其弹性模量E=205.8 GPa,泊松比μ=0.3,弹性件的力学特性由“二阶四项式”Mooney-Rivlin模型表征,利用橡胶材料的单轴拉伸、平面剪切试验数据,拟合得到弹性件材料常数如表2所示,模型和试验对比见图8。

(a)单轴拉伸
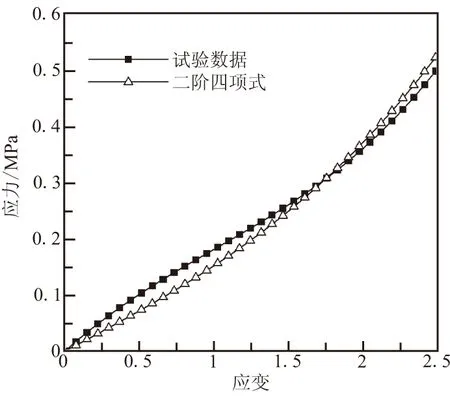
(b)简单剪切
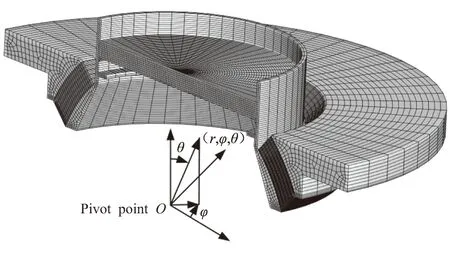
图9 柔性接头有限元计算网格Fig.9 Finite element computational meshes of flexible joint

表2 弹性件材料参数Table 2 Material parameter of elastormer
3.2.4 计算结果
图10是柔性接头各层弹性件在压强和摆角作用下的剪切应变εrθ的云图,图11是φ=0°和180°剖面内各层弹性件沿其中心弧长方向的剪切应变εrθ分布(从弹性件内侧至外侧)。

图10 9 MPa燃烧室压强4.31°摆角下弹性件 剪切应变εrθ云图Fig.10 The elastomer shear strain εrθ distribution at p=9 MPa,δ=4.31°

(a)0°剖面剪切应变

(b)180°剖面剪切应变
可看出,在9 MPa燃烧室压强和4.31°摆角载荷作用下,接头弹性件在φ=0°剖面和φ=180°剖面的最大剪切应变εrθ在1.5左右,与材料的剪切试验拐点基本一致。因此,柔性接头的弹性比力矩在振幅为4.31°时出现拐点,说明弹性件的超弹性是影响柔性接头弹性比力矩的重要因素,而最终决定接头弹性比力矩变化规律的是橡胶的Payne效应和超弹性。
3.3 不同振幅下各力矩随频率的变化
图12是不同振幅下柔性接头各个力矩随频率的变化关系。
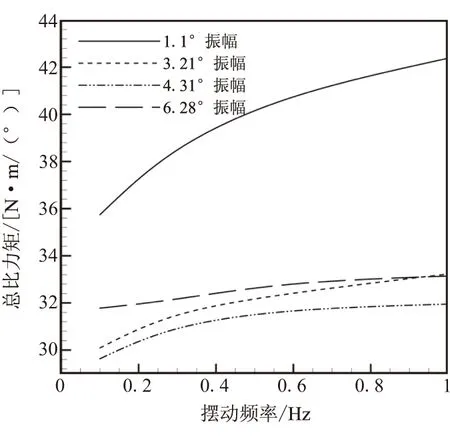
(a)总比力矩
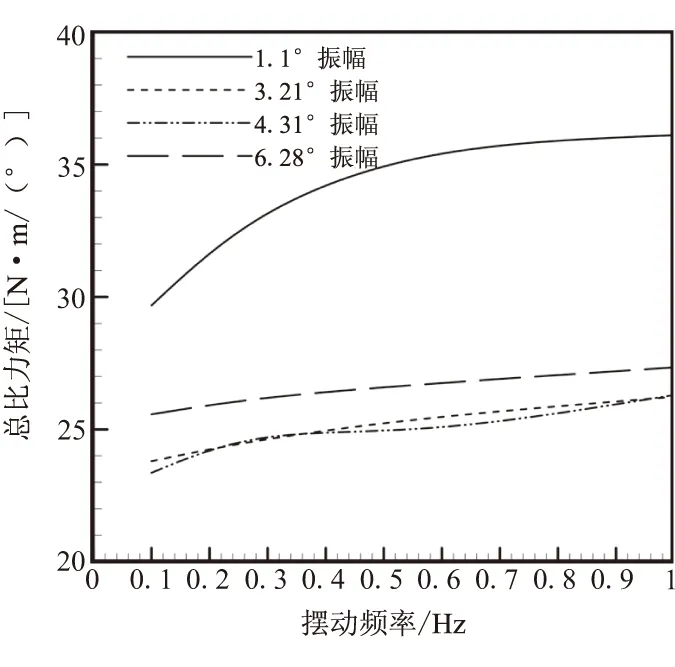
(b)弹性比力矩
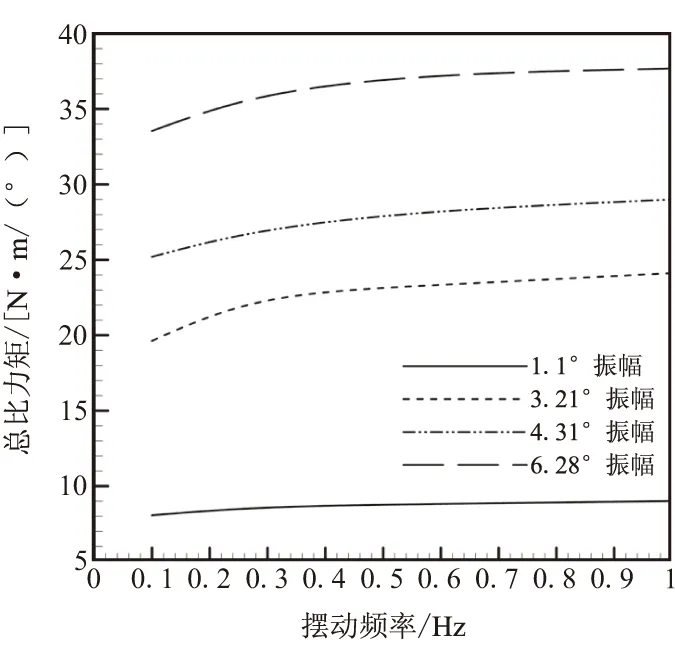
(c)摩擦力矩
可看出,在振幅不变的情况下,弹性比力矩、摩擦力矩和总比力矩都随着频率的增加而增加,但不同振幅下随频率的变化关系不同,弹性比力矩和总比力矩在小振幅激励下随频率的变化明显,1.1°振幅下尤为明显,而摩擦力矩在1.1°振幅激励时,随频率的变化不大,在其它振幅激励下,随频率的变化明显,但0.1 Hz和1 Hz的摩擦力矩数值差在各个振幅激励下基本相同,柔性接头的弹性比力矩和总比力矩随着振幅的增大先减小、后增大,而摩擦力矩则随着振幅的增大而增大。
4 结论
(1)柔性接头的摆动力矩主要由弹性比力矩和摩擦力矩组成,在振幅保持不变时,弹性比力矩、摩擦力矩和总比力矩都呈非线性增大趋势,且增大的速率随摆动频率的增大而减小。
(2)柔性接头的弹性比力矩和总比力矩随振幅的增大先减小、后增大,且拐点出现在振幅为4.31°时,此时各层弹性件的剪应变εrθ在1.5左右,这和橡胶材料的剪切试验曲线拐点基本吻合,说明橡胶材料性能和其Payne效应是影响柔性接头总比力矩和弹性比力矩的重要因素,而摩擦力矩随振幅的增大而增大,对于固定的柔性接头,库仑摩擦力矩在一定燃烧室压强和振幅下才是定值。
(3)各个振幅下柔性接头弹性比力矩、总比力矩和摩擦力矩随频率的变化并不相同,小振幅下弹性比力矩和总比力矩随频率的变化明显,而大振幅下摩擦力矩随频率变化明显,但0.1 Hz和1 Hz摆动条件下,摩擦力矩的差值变化不大。
[1] Shimon Shani,Shlomo Putter,Arie Peretz,et al.Development of a high-performance flexible joint for thrust vector control[R].AIAA 95-3017.
[2] 林培基,高峰.推力矢量对防空导弹作战效能的影响[J].飞航导弹,2009(1):56-57;64.
[3] 吉礼超,宋贵宝.防空导弹控制方法的研究现状及展望[J].战术导弹技术,2009(3):54-59.
[4] Wassom S R,Faupell L C,Perley T.Integrated aerofin/thrust vector control for tactical missiles[J].Journal of Propulsion and Power,1991,7(3):374-381.
[5] Caveny L H,Geisler R L,Ellis R A,et al.Solid rocket enabling technologies and milestones in the united states [J].Journal of Propulsion and Power,2003,19(6):1038-1066.
[6] Olsen K E,Walsh J J,Thomas E L.Navy terrier LEAP third-stage propulsion[C]//AIAA Missile Sciences Conference.Monterey,C A,November 7-9,1994.
[7] Uhrig G,Roussille C.Design drivers and technologies for solid propulsion of interceptors[C]//1st AAAF International Conference on Missile Defense.Arcachon,France,February 3-5,2003.
[8] Avio.Aster 30 [EB/OL].http://www.aviogroup.com/files/catalog/pdf/motore_per_aster_30_25.pdf.
[9] 陈汝训,刘铭初,李志明,等.固体火箭发动机设计[M].北京:中国宇航出版社,2005.
[10] 杨世学.柔性喷管频响特性及传递函数的分析计算[J].推进技术,1991,10(5):7-15.
[11] 刘志武.柔性接头频率特性的计算方法研究[J].固体火箭技术,1998,21(4):18-21.
[12] Woodberry R F H,Zeamer R J.Solid rocket thrust vector control[R].NASA SP-8114,1974.
[13] 张晓光,刘宇,任军学,等.小型柔性接头推力矢量性能试验研究[J].航空动力学报,2012,27(12):2836-2841.
[14] M Berg.A model for rubber springs in the dynamic analysis of rail vehicles[J].Proceedings of the Institution of Mechanical Engineers,Part F:Journal of Rail and Rapid Transit,1997,211(2):95.
[15] Payne A R,Whittakers R E.Low strain dynamic properties of filled rubber[J].Rubber Chem.Tech.,1971,44(2):440-478.
[16] Payne A R.The dynamic properties of carbon black-loaded natural rubber vulcanizates[J].Journal of Applied Polymer Science,1962,6(19):57-63.
(编辑:崔贤彬)
Numerical and experimental investigation on properties of miniature flexible joint torque
YANG Jing-xian1,WANG Chao2,REN Jun-xue2,LIU Yu2,HAO Wen-qiang2,CAO Xi-wei3
(1.Shanghai Xinli Power Equipment Institute,Shanghai 200125,China;2.School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China;3.Study and Development Center of China Academy of Launch Vehicle Technology,Beijing 100076,China)
In order to study the properties of flexible joint torque in a certain motor pressure,a miniature flexible joint with silicone rubber elastomer was designed.The dynamic characteristics of flexible joint under 9 MPa vessel pressure were tested and the curves of torque versus vector angle for the flexible joint at different amplitudes and frequencies were obtained.The friction torque was obtained through the 0° vector angle torque and the spring torque was calculated by the near-linear part of the torque versus vector angle curve.In addition,the influence of excitation frequency and amplitude on the three kinds of torque were studied.Results show that coulomb friction torque increases as the excitation amplitude increases.The viscous friction torque increases with the increase of swing frequency.The spring torque and the total ratio torque increase as the swing frequency increases while decrease with the amplitude increases in a certain range and then increases as the amplitude in-creases.
flexible joint;thrust vector control;friction torque;spring torque;total ratio torque
2014-09-15;
:2014-12-26。
基金基目:上海航天科技创新基金(SAST201258)。
杨敬贤(1978—),男,高级工程师,主要从事固体火箭发动机研究。E-mail:lamb_yang@yahoo.com.cn
V435+.23
A
1006-2793(2015)04-0497-06
10.7673/j.issn.1006-2793.2015.04.009
