准极端Reissner-Nordström黑洞对Dirac粒子的散射

吕 嫣, 花 巍

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)



准极端Reissner-Nordström黑洞对Dirac粒子的散射

吕 嫣, 花 巍

(沈阳师范大学 物理科学与技术学院, 沈阳 110034)

在Reissner-Nordström时空下,给出分离变量后的Dirac方程的径向方程和角向方程。按照Chandrasekhar的方法,通过定义乌龟坐标变换,将径向耦合方程退耦成独立的一维波动方程,并给出方程中势的表达式。考虑到极端Reissner-Nordström黑洞内外视界是重合的,这将导致黑洞的质量和电荷量相同。在准极端Reissner-Nordström背景时空下,讨论了当粒子的能量大于势垒高度时,Dirac粒子被黑洞的散射情况。首先,将势函数用一组阶梯函数代替;之后,利用量子力学的方法给出透射反射系数以及波函数的数值变化曲线;最后,比较分析不同质量的粒子被散射的情况。从结果来看,不同质量Dirac粒子的散射是明显不同的,质量越大的粒子散射越强。从这个角度来讲,黑洞也可以看做是一个质量摄谱仪。

准极端Reissner-Nordström黑洞; Dirac粒子; 散射; 乌龟坐标

0 引 言

自从霍金发现黑洞存在热辐射之后[1],黑洞的量子特性越来越受到人们的关注。目前为止,已经有各种各样的方法和手段被应用于研究各种背景时空下黑洞的辐射和散射问题[2-13]。本文所研究的准极端Reissner-Nordström(RN)黑洞对Dirac粒子的散射问题,实际上是求解该背景时空下的Dirac方程。弯曲时空中Dirac方程的解一方面反映了高度弯曲时空附近天体的自身演化图像,另一方面也可以解释并预言Dirac粒子在弯曲时空中的行为,后者对于进一步研究黑洞的热性质又具有极其重要的理论意义。

1 波动方程

RN时空中的线元形式为

其中:M是黑洞质量;Q是黑洞电荷量。根据文献[14],RN时空中的Dirac方程可分离为径向和角向方程,径向方程为

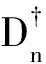
且有

这里:n是整数或半整数;σ代表入射波的频率;m是粒子的静止质量;λ是Dirac方程的本征值;Δ可称作视界函数。

分离变量后的角向方程为

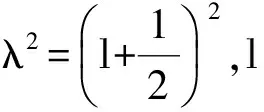
定义乌龟坐标

其中

并且

上式中:r±为黑洞两视界的视界半径;κ±为相应的表面引力。

按照Chandrasekhar的方法[14],径向耦合方程(2)、(3)可以被退耦为一维波动方程

(14)式中势垒的表达式为

2 波动方程的解

在每一阶梯上局域反射透射系数有如下形式

在边界处采用无反射的内边界条件,即Vn→0,Rn→0。图2给出了不同质量粒子的即时透射反射系数,参数选择情况是:σ=0.8,m=0.8(实线),m=0.75(虚线),m=0.7(点划线)。在边界处,势为0,所有粒子反射系数均为0,随着远离边界,所有粒子的反射系数均在增加,而透射系数相应减小。可以看出,质量越大的粒子反射系数越大而透射系数越小,这意味着质量小的粒子更容易穿越势垒。图3给出了相应粒子的波函数变化曲线,图3a代表波函数的实部,图3b代表波函数的虚部。在靠近边界处,不同质量粒子的波长、振幅近似相同,随着远离边界,质量较大的粒子波长更长,振幅更大,其散射更为明显。

图1 势与阶梯势

图2 反射系数与透射系数

图3 波函数

3 结 论

本文研究了准极端RN黑洞对Dirac粒子的散射,包括透射反射系数和波函数。采用阶梯势的方法得到全空间的透射反射系数以及波函数的变化情况。透射反射系数是逐点定义的,因此也可以称作即时透射反射系数。在所讨论的情况中,不同质量的粒子散射情况明显不同,质量越大的粒子散射越强,可以推断不同能量的粒子入射黑洞,散射情况也会明显不同,所以黑洞可以看作是一个质量(或能量)摄谱仪。以上讨论的是入射粒子的散射,若根据霍金辐射考虑事件视界处产生的出射粒子,则在无穷远处的平均粒子数应为霍金辐射谱与势垒穿透系数的乘积。

[ 1 ]HAWKING S W. Black hole explosions?[J]. Nature, 1974,248:30-31.

[ 2 ]PARIKH M K, WILCZEKil F. Hawking radiation as tunneling[J]. Phys Rev Lett, 2000,85(24): 5042-5045.

[ 3 ]ZHANG Jingyi, ZHAO Zheng. Massive particles’ black hole tunneling and de sitter tunneling[J]. Nucl Phys B, 2005,725(1/2):173-180.

[ 4 ]GUO Guanghai, GUI Yuanxing, TIAN Jianxiang. The real scalar field in extreme RNdS space[J]. Gen Relativ Gravit, 2005,37(7):1323-1330.

[ 5 ]GUO Guanghai. Real scalar field scattering in the nearly extremal Schwarzschild desitter space[J]. Chin Phys B, 2010,19(11):110403.

[ 6 ]LYU Yan, HUA Wei. Solution of Dirac equation around a charged rotating black hole[J]. Chin Phys B, 2014,23(4):040403.

[ 7 ]SHAO Jianzhou, WANG Yongjiu. Scattering and absorption of particles by a black hole involving a global monopole[J]. Chin Phys B, 2012,21(4):040404.

[ 8 ]CHAKRABARTI S K, MUKHOPADHYAY B. Scattering of Dirac waves off Kerr black holes[J]. Mon Not R Astron Soc, 2000,317(4):979-984.

[ 9 ]MUKHOPADHYAY B,CHAKRABARTI S K. Semi-analytical solution of Dirac equation in Schwarzschild geometry[J]. Class Quant Grav, 1999,16(10):3165-3181.

[10]LYU Yan, GUI Yuanxing. Numerical solution of Dirac equation in Schwarzschild-de sitter spacetime [J]. Phys Scr. 2007,75(2):152-156.

[11]LYU Yan, CUI Song, LIU Ling. The solution of Dirac equation in quasi-extreme Reissner-Nordström de sitter space[J]. Mod Phys Lett A, 2009,24(30):2433-2443.

[12]吕嫣,方戈亮,徐琦. Schwarzschild-de Sitter度规下旋量场方程的解[J]. 沈阳师范大学学报:自然科学版, 2006,24(4):426-429.

[13]BREVIK I, SIMONSEN B. The scalar field equation in Schwarzschild-de Sitter space[J]. Gen Relativ Gravit, 2001,33(10):1839-1861.

[14]CHANDRASEKHAR S. The mathematical theory of black holes[M]. New York: Oxford University press, 1983.

[15]CHAKRABARTI S K. On mass-dependent spheroidal harmonics of spin one-half[J]. Proc R Soc Lond A, 1984,391:27-38.

Scattering of Dirac particles off quasi-extreme Reissner-Nordströmblack holes

LYUYan,HUAWei

(College of Physical Science and Technology, Shenyang Normal University, Shenyang 110034, China)

Dirac equations are separated into radial and angular equations in Reissner-Nordström (RN) geometry. By tortoise coordinate transformation, the radial parts of Dirac equations are decoupled into independent one-dimensional wave equations according to Chandrasekhar’s method. The form of the potential in the wave equations is also given. For extreme RN black holes, the two black hole horizons are coincidence, which leads to the equal mass and the electric charge of the black hole. In quasi-extreme Reissner-Nordström geometry, the case that the energies of the waves are greater than the height of the potential barrier is considered. First, the potential is replaced by a collection of step functions. Second, the reflection and transmission coefficients and the wave functions are computed by quantum mechanics method. Last, the solutions to Dirac equations with different masses are compared. The results show that Dirac particles with different mass are scattered obviously different, the greater the mass is, the stronger the scattering is. Therefore, the black hole can act as a mass spectrograph.

quasi-extreme Reissner-Nordström black holes; Dirac particles; scattering; tortoise coordinate

2015-03-08。

国家自然科学基金青年科学基金资助项目(11301350)。

吕 嫣(1978-),女,辽宁沈阳人,沈阳师范大学副教授,硕士。

1673-5862(2015)03-0405-04

O412.1

A

10.3969/ j.issn.1673-5862.2015.03.019