花园幽径模式行进错位的量化研究:计算语言学视角

2015-04-21杜家利于屏方

中文信息学报 2015年5期

关键词：幽径频数错位

杜家利, 于屏方

(1．广东外语外贸大学词典中心，广东广州 510420;2. 南京大学外国语学院，江苏南京 210093;3. 广东外语外贸大学中国语言文化学院，广东广州 510420)

花园幽径模式行进错位的量化研究:计算语言学视角

杜家利1，2, 于屏方3

(1．广东外语外贸大学词典中心，广东广州 510420;2. 南京大学外国语学院，江苏南京 210093;3. 广东外语外贸大学中国语言文化学院，广东广州 510420)

该文讨论了花园幽径模式行进错位过程中的困惑商指数。非对称性信息断层的存在导致解码呈现否定之否定的螺旋上升态势。行进错位的潜在效应幅度可通过困惑商指数得到测定。基于大数据语料库统计方法和在线剖析器分析方法，我们测算出优选结构困惑商指数介于(-∞，1]；非优选结构困惑商指数介于[1,2]；两结构临界值分别为0.72和1.28；歧义域为[0.72,1.28]。结论认为，多结构频数差异是导致困惑商指数变化的根本；行进错位的幅度和非对称性信息补偿的强度均与困惑商指数相关；基于统计的困惑商指数可对局部歧义的复杂句结构提供前瞻性解码信息。

计算语言学；花园幽径模式；行进错位；局部歧义；困惑商

1 引言

花园幽径(Garden Path: GP)模式是一种局部歧义的回溯性顿悟模式，其解码呈现“先期伪平衡——中期再平衡——后期优化平衡” 的螺旋上升态势。这种折返性错位效应恰似花园中走入了一条貌通而实不畅的幽径。行进错位(Processing Breakdown)[1]在诱发回溯的同时，其非对称性信息形成了断层并最终为认知的顿悟跨越提供了可能。语义触发点出现后，先期原型模式被颠覆，非原型的备选模式适时启动，最终结构得以重组并实现否定之否定的解读。

例如，在“The man lent the book never returned it.[2]”中，[[The man]NP [lent the book]VP]S是原型结构，系统首先采纳Vpast tense→{lent}进行解码，并实现[NP+VP]S的平衡结构。但随着触发点returned的出现，原来的平衡结构被打破，系统被迫再平衡，备选模式Vpast participle→{lent}得以启动。最后，优化后的平衡结构变成了[[The man]NP+[lent the book]CP+[never returned it]VP]S。系统在经历了行进错位后折返回溯并实现了跨越式解码。

作为局部歧义的花园幽径模式，其特有的行进错位效应和信息断层现象激发了诸多学者的研究热情。如基于眼动的记忆模型研究[3]，言语停顿所致的局部歧义研究[4]；结构启动研究[5-9]，认知系统的顿悟性和控制性研究[10-16]，统计和算法研究[17-19]，语义特征研究[20-22]，词汇期待研究[23-25]等各种多维度研究。本文将从花园幽径模式行进错位过程中产生的困惑度为中心进行量化讨论，利用计算语言学方法分析行进错位的“肯定——否定——二次否定”的解码特征。

2 花园幽径模式的行进错位研究

花园幽径模式解读主要分为三个主要阶段: 前期顺畅的信息伪对称阶段、中期困惑的信息断层阶段、后期跨越的信息再对称阶段[26]。

2.1 花园幽径模式的解码特征

花园幽径模式出现前期，信息具有表象的趋对称性。这个发生在注视初期的加工反映了大脑对花园幽径理解的初始模式。随着相关附加信息的涌入，信息表象的趋对称感逐渐被现实的断层感所取代，直到解码无法依靠前行信息继续进行加工。认知系统要求对初始模式回视、补充新的信息，然后对获取的总信息重新加工，再分析效应出现。信息得到补偿弥合后，先前信息伪对称的失衡状态被真平衡所取代，语言加工重新回到正常轨道并完成解码。

花园幽径模式的设置者，不论其目的是研究还是寻求语言效果，与被试相比都拥有更多的解码信息。被试误入花园幽径之时，就是期待信息快速补偿之时。当解歧点出现，缺损信息得到补偿，断层感得到弥合，信息变得重新对称，语言加工变得顺畅。

据此分析，我们认为花园幽径模式的解读就是当信息出现断层无法继续构建成功模式时对非对称性信息的快速补偿。由此，我们提出花园幽径模式非对称性信息补偿假说[27]。

该假说包括三个主要部分: 花园幽径模式解读中的信息是非对称性的，存在信息断层的可能；花园幽径模式解码路径呈现否定之否定的螺旋态势，存在补偿性回归的可能；花园幽径模式具有信息逆向选择的超常规解释，存在顿悟跨越的可能。

2.2 行进错位研究的非对称性信息补偿效应

非对称性信息补偿效应模型采用“三四五”主体构架，即涵括三个解码部分、四个外围附属部分和五个相关原则。

三个解码部分是非回溯的正常解码；没有正确模式的错误解码；涉及折返顿悟、否定之否定的花园幽径模式解码。

四个外围附属部分涵括词与短语的瞬时匹配；整句匹配；内程序知识库的结构启动、记忆容量和尚好策略；属于外程序知识库的信息密度、经验控制、词汇期待、语义条件和语境限定。

五个相关原则包括西蒙非极致原则、阿克洛夫逆向选择原则、格雷欣法则、瓦尔拉斯均衡和帕累托最优。具体见图1。

非回溯的正常解码流程如下:

a1 输入字符串(Input)；

a2 判定字符串提供的信息与认知贮存信息是否具有暂时性匹配平衡(Balance?)；

a3 肯定答复(Yes)则在整合内程序知识库信息的基础上进行词、短语的瞬时匹配，并形成初始结构(+A)；

a4 受西蒙非极致原则影响，初始结构(+A)与后续字符串整合后形成模式B;

a5 模式B涵括的字串数量在累加过程中受到

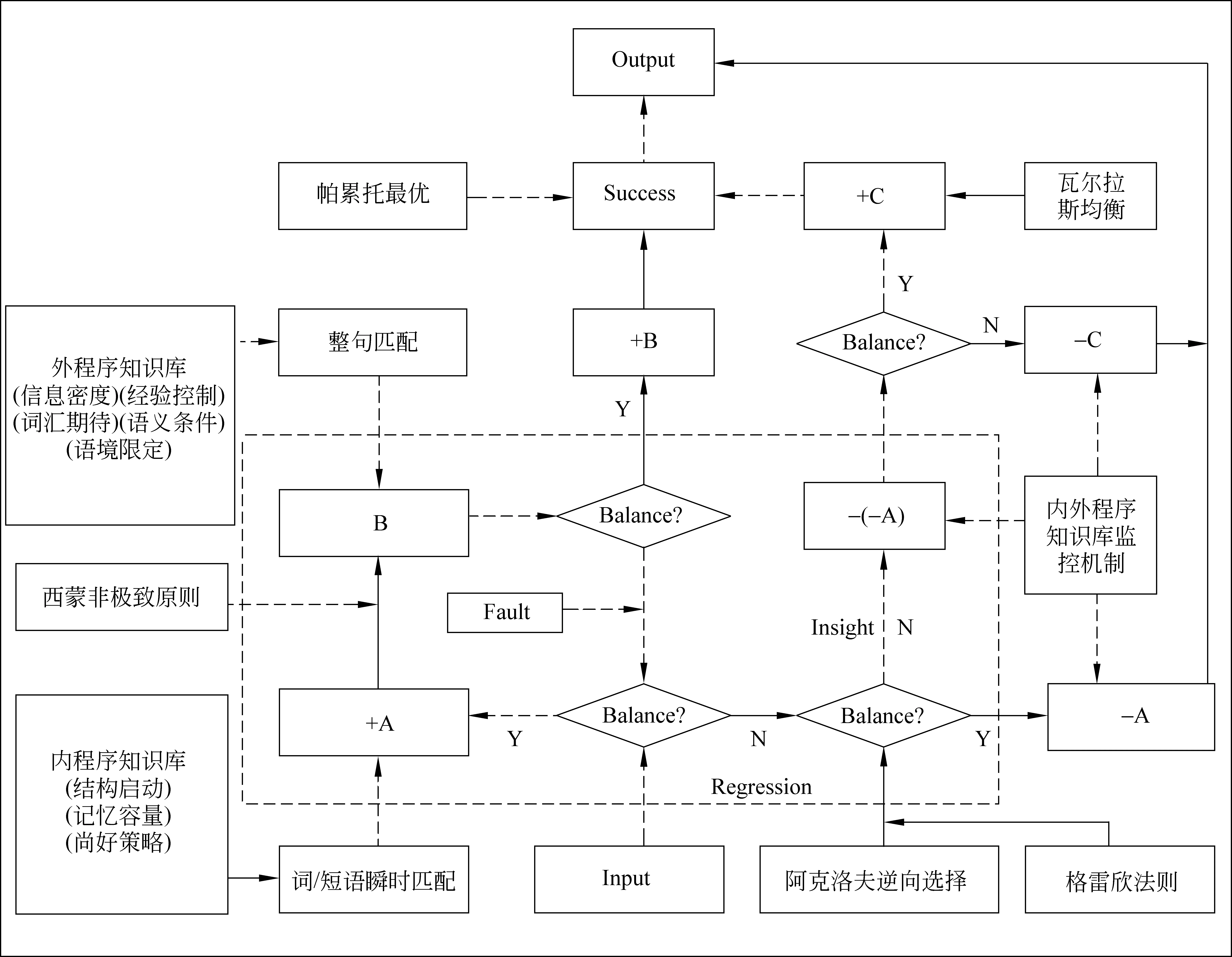
图1 行进错位的非对称信息补偿效应图

外程序知识库信息的影响，并完成整句匹配；

a6 匹配完成的模式B信息势能达到最佳，与全句字串蕴含的信息势能对照(Balance?)；

a7 信息平衡(Yes)则生成终极结构(+B)；

a8 终极结构达到帕累托最优状态后成功解码(Success)；

a9 输出(Output)。

错误解码流程如下:

b1 输入字符串(Input)；

b2 判定字符串提供的信息与认知贮存信息是否具有暂时性匹配平衡(Balance?)；

b3 否定答复(No)则进入下一轮选择；

b4 相对于正常解码形成的暂时初始结构(+A)来说，否定答复认知形成的结构为判定性结构(-A？)，系统判定该结构是否受阿克洛夫逆向选择和格雷欣法则影响；受到影响生成的是否定之否定[-(-A)]结构；不受影响生成的是错误结构(-A)；

b5 判定生成的是否是(-A？)；

b6 肯定答复(Yes)，获得的是结构(-A)，经与内外程序知识库比对确认为错误；

b7 输出(Output)。

花园幽径模式解码流程:

c1-c6与a1-a6相同；

c7 达到最佳信息势能的B模式无法实现与蕴含信息的平衡，认知过载和行进式错位产生；

c8 信息断层(Fault)出现；

c9 解码回溯到初始a2状态(Balance?);

c10 -c12 与b3-b5相同；

c13 否定答复(No)，说明受阿克洛夫逆向选择和格雷欣法则影响，产生了由前期错误结构演变而来的回归(Regression)模式，大量有效信息得到补偿；

c14 顿悟(insight)出现；

c15 否定之否定[-(-A)]结构生成，并受内外程序知识库监控；

c16 完成的[-(-A)]模式信息势能达到最佳，与全句字串蕴含的信息势能对照(Balance?)；

c17 信息达到瓦尔拉斯均衡(Yes)则生成终极结构(+C)；不均衡则经与内外程序知识库比对确认为错误，转至c19；

c18 终极结构达到帕累托最优状态后成功解码(Success)；

c19 输出(Output)。

从上面的分析可以看出，从c1～c15(模型中用虚线的大矩形进行了标注)是花园幽径模式解码的核心区域，涉及信息断层、认知回归、顿悟和否定之否定。螺旋上升是否定之否定的必然结果。解码信息的“先期伪平衡——中期再平衡——后期优化平衡” 形成了“肯定——否定——二次否定”的螺旋上升态势。花园幽径效应初期，原型模式(+A)被激活但不能成功解码，遂被认知判定为伪处理模式，第一次加工(B模式)失败，并导致信息断层后的折返回归。如果要跨越障碍，B需要对(+A)进行否定(即进入-A状态)。花园幽径效应中期，系统回溯后重新进行解码，备用模式(-A)被激活。花园幽径效应后期，备选模式否定后的C模式(即[-(-A)]平衡模式)得到构建。由于(-A)是B对(+A)的否定，终结模式C又是对(-A)的否定，那么C必然是对模式(+A)的否定之否定。信息由第一次加工的不对称失败到第二次的对称成功，经历了Z型的否定之否定的认知轨迹，在信息断层后通过回归和顿悟获得了补偿性信息，完成了螺旋上升的认知轨迹。

3 花园幽径模式解码的困惑商指数

困惑商(CQ: Confusion Quotient ) 类似智商IQ，情商EQ以及财商FQ，这里指由于花园幽径效应存在所导致的认知困惑程度。商值高，惑度则高。

智商(IQ: Intelligence Quotient)意指知觉能力、观察能力、思考能力、推理能力和理解能力等诸方面的系统评测，包括注意力、判断力、记忆力、语言分析能力等各领域的智能表现，还有对知识的掌握及分析问题和解决问题的能力等。情商(EQ: Emotional Intelligence Quotient)意指情绪、情感、意志以及耐受挫折等方面的品质评测。财商(FQ: Financial Quotient)，意为一个人与金钱打交道的能力。

我们这里提出“困惑商CQ”的概念，特指由于非对称信息的补偿所产生的认知过载现象，包括行进式错位和信息断层，蕴含顿悟式回溯解码，是高信息势能向低信息势能的流动。就像信息熵代表“不确定性”一样，当低频、高困惑商的非优选结构颠覆高频、低困惑商的优选结构时，认知系统需要为成功解码提供足够多的补偿性解释信息，这就为认知系统带来了额外的认知负担。

非对称信息的补偿是由超出常规预期的次优选项导致的。在花园幽径模式中必然存在一个优选结构和次选结构，而且通常这种结构的优选与否在统计学意义上具有差异性。

优选结构是认知系统的缺省模式，在解码前享有较高的使用频数，其曾经存在的频数越高对后续认知折返的阻力越大，产生的顿悟效应越明显，认知过载现象也越突出。也就是说前期观察频数正偏离预期频数的差值越大(观察频数大于预期频数)，越可能充当优选结构。

次选结构则相反。如果认知系统中前期观察频数负偏离预期观察频数的差值越大(观察频数小于预期频数)，越不可能充当优选结构，其非对称导致的信息补偿的可能越大，要求越强烈，具有的认知扭矩越大。

在花园幽径模式中，折返性顿悟现象所需要的信息补偿来源于认知的多个系统，如词汇、句法、语义、语用等，它们共同作用的结果可完成花园幽径模式的解读，弥合认知扭矩不平衡带来的信息断层，实现信息补偿。所以，我们认为对非对称信息的补偿计算需要如下几个变量:

基于语料库的某项属性的观察频数(O: Observer)；

某项属性的预期频数(E: Expecter)；

参与信息补偿的属性单元数量(n: number)；

属性单元(i)；

困惑商(CQ: Confusion Quotient )；

非对称信息所需要的困惑商值(V: Value)。下文中具体困惑商值的简写为Vcq，下标cq表示困惑商。

(1)

式(1)中(Oi-Ei)表示对属性i来说，观察频数偏离预期频数的距离；

(Oi-Ei)/Ei表示偏离距离与预期频数的比值，负值表示负偏离，正值表示正偏离；

1-(Oi-Ei)/Ei表示正负偏离以1为基点向两侧辐射，正偏离辐射范围为(-∞,1]，负偏离范围为[1，2]。

取和公式表示所有参与信息补偿的属性所具有的偏离比值可以进行累加，然后取平均值。

从正负偏离的辐射范围可以看到计算也是具有不对称性的，次选结构的偏离值在一个封闭域内，而优选结构的偏离值则是半开放的。

例1Thehorseracedpastthebarnfell[5].

以例1的动词raced说明如下(表1)。

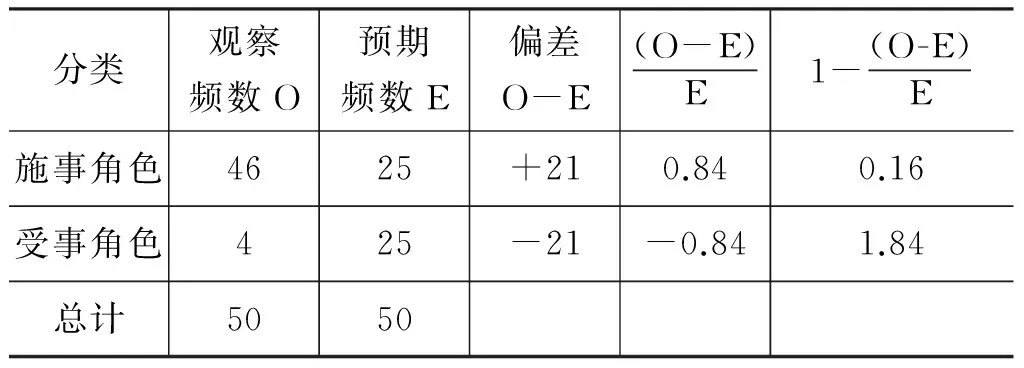
表1 动词raced非对称信息困惑商

如表1，由于这里只计算了动词的困惑商，句中其他结构成分没有涉及，所以不存在平均值的问题，即这里是n=1的状态。施事角色属性的困惑商为0.16，而受事角色困惑商为1.84，后者造成的认知扭矩更大，需要更多的信息补偿才能实现平衡，完成解码。

假定某动词X观察频数和预期频数相等，那么不对称情况被消解，两者差值为零，获得的困惑商为1。这是平衡解码的理想状态。

假定某动词X观察频数无限小于预期频数，即观察频数近乎为零，则困惑商约为2。这种极端低概率的解码模式一旦被采纳，需要认知系统释放来弥补信息断层的补偿信息量也超乎想象。这就是说不对称信息困惑商最大为2。

假定需要进行不对称信息补偿的某动词X观察频数无限放大，由于不对称性的存在，该次选结构的频数不会超过优选结构频数，也就是说它的观察频数的最大值就是预期频数。此时，观察频数和预期频数相等，困惑商为1。这表明次选结构的不对称困惑商最小为1。

这样，次选结构不对称信息困惑商区间为[1，2]。越接近1表示需要补偿的信息少，信息趋向于对称，引起顿悟的可能性就小，产生折返性回溯的花园幽径效应可能性也小，而出现通达性歧义的可能性增大。越接近2则情况相反，认知扭矩不断累加，直至达到超出认知总容量的极点。

对优选结构来说，观察频数的最低点就是预期频数，低于该频数结构就不再是优选结构了。因此，不对称困惑商最大为1。随着观察频数对预期频数的不断超越，所需要的信息困惑商越来越小。

假定某动词Y在认知中具有五个可供选择的属性，抽样总数为500，那么理论预期频数为100。如果每个属性在语料库中都观察到100个符合各自属性的频数，那就是理想的帕累托最优状态。假定有一个属性的观察频数达到了490，那么需要进行信息补偿的值为-2.90。这表示该优选模式已经具备了足够的解码信息量，它产生的是正偏离，不需要再对该属性进行信息补偿。

优选结构产生的困惑商从1不断向负无穷辐射。越接近1表示优选结构需要补偿的信息越多，信息趋向于对称，而基于频数的优选结构倾向受到极大挑战；相反，困惑商向负无穷辐射过程中，需要额外补偿说明的信息越少，该优选结构信息自足量越大，越容易在解码时被认知系统优先采纳，困惑程度越来越低，直至该结构解码成为一种非受控的完全无意识状态。

非对称性信息补偿通常是以优选结构和次选结构的频数统计差异性存在为条件的，所以，我们需要根据卡方检验的临界值测算出可能诱发花园幽径效应的非对称困惑商的临界值。超出临界值则表明频数具有显著性差异，信息困惑商也具有区别性特征。如果实际统计值没有超出临界值则表明频数不具有统计意义的显著差异，信息处于非补偿的统计意义的对称状态。

假定显著水平为.05，自由度为1，理论临界值则为3.84(可查阅SPSS值附录)。

假定实际解码中涉及两个义项属性且可能诱发花园幽径效应的次选属性频数为X，统计中总观察频数为50，那么优选属性频数则为50-X。根据卡方检验公式推导如下(表2)。

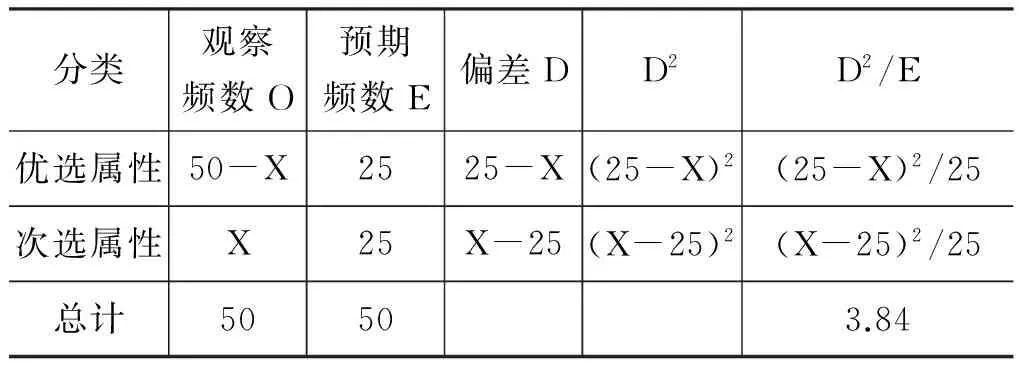
表2 次选属性临界观察频数推导表

如表2所示，(X-25)2/25=1.92, X=18。这说明具有优选结构和次选结构的观察频数临界比为32∶18。比值越大，说明优选和次选结构频数差异越悬殊，如果诱发花园幽径效应产生的认知困惑度也越强烈；比值越小，两结构频数趋同，统计学意义的差异不断弥合，呈现非回溯通达性歧义的可能性加大。依据以上数据我们可以推导出非对称信息困惑商的临界值，具体如表3所示。

表3 次选属性非对称信息补偿临界值测算表

表3中优选结构和次选结构的临界观察频数中次选属性的观察频数是18，预期频数是25，频数偏差为18-25=-7，频数偏差与预期频数之比为-7/25=-0.28。根据困惑商计算公式，此结构属性n=1, 困惑商值CQ=1-(-0.28) =1.28。这表明次选属性非对称信息补偿临界值为1.28，说明如果实际解码中困惑商大于临界值，诱发花园幽径效应的可能性增大，信息断层后需要信息补偿的强度也增大。困惑商从1.28向2.00变化时(前面已验证次选结构CQ最大值为2)，认知扭矩处于不断加大状态，一旦次选属性颠覆优选属性成为正确的解码模式，那么大扭矩产生的认知困惑和过载现象将得到释放；相反，从1.28向1.00变化时(前面已验证次选结构CQ最小值为1)，认知扭矩变小，信息不对称可能性减少，认知困惑程度减弱，出现“多车道通行”的通达性歧义可能性增大。

4 基于困惑商指数的行进错位量化研究

下面我们以英语中的主导从句和附属关系从句为例讨论行进错位的困惑商指数。

主导从句(Matrix Clause)与附属关系从句(Reduced Relative Clause)不对称是指主动词及物被动态和不及物主动态属性分布不均衡导致的结构歧义。主动词(Matrix verb)具有及物和不及物两种属性，通常不及物主动态属性是优选结构。这样，在与前行名词构建的暂时结构中形成的是主谓结构。但是，随着解码推进，次选结构的主动词及物被动态属性被激活，优选结构被颠覆，折返性回溯产生。在英语中，过去式与过去分词的同形为这种结构歧义的存在提供了便利。请见例2和例3。

例2 The boat floated down the river sank[28].

例2出现了花园幽径效应，其根本原因在于动词floated的属性变化，致使初期构建的主导从句结构被后期附属从句结构所颠覆。我们分别利用BNC随机抽样计算不对称困惑商。

如表4所示，动词floated的被动语态的频数是13，不对称信息困惑商为Vcq=1.48>1.28临界值。

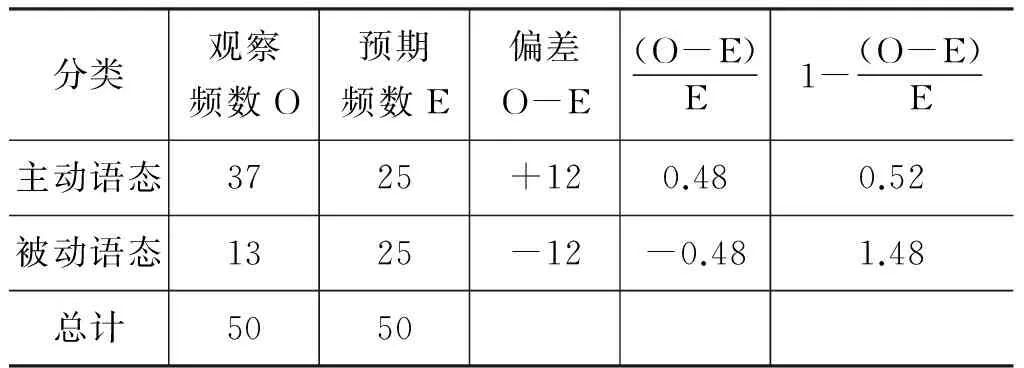
表 4 动词floated 的主被动语态不对称值对比

这说明被动语态作为次选结构的认知扭矩较大，颠覆优选结构后，获得的补偿性信息量也较多。这种低频数的解码模式对于基于概率的Stanford Parser来说，解读有困难。请见Stanford Parser对该句的错误剖析:

*(ROOT

(NP (DT The) (NN boat))

(VP (VBD floated)

(PRT (RP down))

(SBAR

(NP (DT the) (NN river))

(VP (VBD sank)))))))

如上所示，解析器无法正确分析该句结构，the river sank被误认为是从句结构，而且floated down the river作为附属关系从句的解码也无法在剖析中体现。正确结构中主动词应该是sank，附属关系从句作为定语的是floated down the river。动词floated应该认定为过去分词(VBN floated)而不应该是过去式(VBD floated)。成功的剖析如下:

(ROOT

(NP

(NP (DT The) (NN boat))

(VP (VBN floated)

(PP (IN down)

(NP (DT the) (NN river)))))

(VP (VBD sank))))

例3 The dog walked to the park chewed the bone[29].

例3也是花园幽径句。动词walked的过去式和过去分词同形，其语态属性既可以是主动也可以是被动。我们先计算两个选项的非对称困惑商。

如表5所示，动词walked的被动语态的频数是0，不对称信息困惑商为Vcq=2 >1.28临界值。这

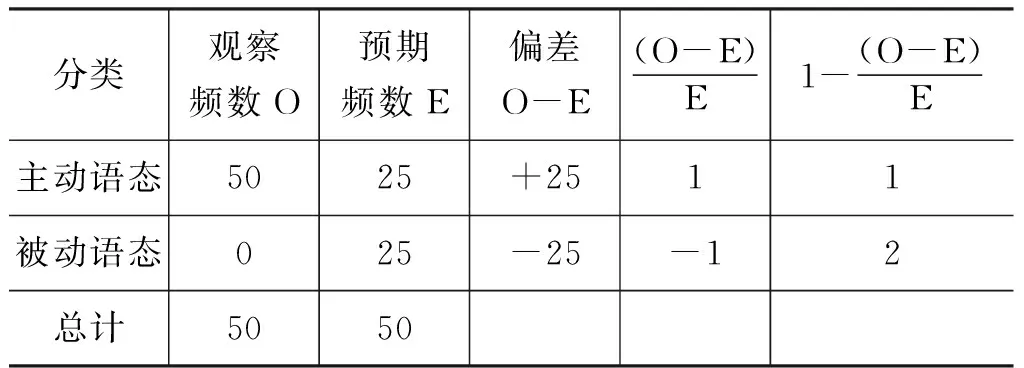
表 5 动词walked的主被动语态不对称值对比

说明被动语态结构从理论上说认知扭矩达到无法超越的最大值，从实践意义说，该句应该是Gibson博士自己创造的花园幽径句，其在语料库中出现的概率近乎可以忽略。这样极端的低概率在解码中引起的颠覆效应将是空前的，极端不对称解码所需要的信息补偿量也会让读者产生极强烈的认知困惑，并在解码成功后诱发令人震撼的顿悟感。这种句子对于基于概率语料库的Stanford Parser来说是不存在剖析正确的可能，只能依靠规则而不是统计实现解码。请见Stanford Parser对该句的错误剖析:

*(ROOT

(SINV

(NP (DT The) (NN dog))

(VP (VBD walked)

(PP (TO to)

(NP (DT the) (NN park)))))

(VP (VBD chewed))

(NP (DT the) (NN bone))))

正如我们分析的那样，Stanford Parser无法完成解码。系统把整个结构解读为SINV而不是S，参照系统代码的解释，我们可以知道SINV[30]即“Declarative sentence with subject-aux inversion, top level labelling apart from S, usually for complete structure”，也就是具有主语翻转功能的完全陈述句结构(an inverted S structure)，例如，在“Marching past the reviewing stand were 500 musicians”句中的结构。Marcus et al具体结构解释如下:

图2 代码SINV的结构样例

如图2可知，我们需要的The dog walked to the park chewed the bone剖析结构并不是解析器剖析的SINV结构，也不存在主语翻转问题。该句从规则语法角度可以很容易判定是一个附属关系从句结构。把动词walked理解成过去分词(VBN walked) 就能成功解码。正确剖析如下:

(ROOT

(NP

(NP (DT The) (NN dog))

(VP (VBN walked)

(PP (TO to)

(NP (DT the) (NN park)))))

(VP (VBD chewed)

(NP (DT the) (NN bone)))))

从上面的分析可以看出，主导从句与附属关系从句的不对称源于动词过去分词和过去式的同形歧义，过去式形式可以附着于前行词作为全句的主动词(matrix verb)出现；过去分词形式也可以附着于前行词作为附属关系从句出现，并由此引发主动态和被动态的非对称性选择。通常情况下，作为主动词的过去式形式具有认知原型特点，次选结构取代优选结构将产生认知过载现象。类似的花园幽径句还有“The performer sent the flowers was pleased”, “The woman brought the flowers smiled broadly”[30]等。

5 结语

花园幽径模式源于非对称信息补偿的认知过载，是行进式错位和信息断层相互作用的结果。困惑商指数可用于量化分析信息断层所致的非对称性信息补偿。我们测算后可知，优选和非优选结构困惑商指数从1分别向负无穷和2辐射。向1靠近，两结构趋向于对称；向负无穷靠近，优选结构信息自足量增大，原型特点凸显；向2靠近，非优选结构断层效应激增，行进中的错位感加大。优选和非优选结构的困惑商指数临界值分别0.72和1.28。超出临界值则表明两结构频数具有显著性差异，更易导致信息断层和行进错位的出现。研究证明，困惑商指数对花园幽径模式行进错位的幅度和强度具有前瞻性。

[1] B L Pritchett. Garden path phenomena and the grammatical basis of language processing[J]. Language, 1988(64): 539-576.

[2] K Rayner, M Carlson, L Frazier. The interaction of syntax and semantics during sentence processing: Eye movements in the analysis of semantically biased sentences[J]. Journal of verbal learning and verbal behavior, 1983, 22(3): 358-374.

[3] G Altmann, A Garnham, Y Dennis. Avoiding the garden path: Eye movements in context[J]. Journal of Memory and Language, 1992, 31(5): 685-712.

[4] K G D Bailey, F Ferreira. Disfluencies affect the parsing of garden-path sentences[J]. Journal of Memory and Language, 2003, 49(2): 183-200.

[5] T G Bever. The cognitive basis for linguistic structures[A]. In Hayes, J R (ed.), Cognition and the Development of Language. New York: John Wiley and Sons, 1970: 279-352.

[6] K Christianson. Sensitivity to syntactic changes in garden path sentences[J]. Journal of psycholinguistic research, 2008, 37(6): 391-403.

[7] J L Du, P FYu, M L Li. Machine Learning from Garden Path Sentences: The Application of computational Linguistics[J]. International Journal of Emerging Technologies in Learning, 2014,9(6):58-62.

[8] T J Slattery, P Sturt, K Christianson, et al. Lingering misinterpretations of garden path sentences arise from competing syntactic representations[J]. Journal of Memory and Language, 2013, 69(2): 104-120.

[9] R P G van Gompel, M J Pickering, J Pearson, et al. The activation of inappropriate analyses in garden-path sentences: Evidence from structural priming[J]. Journal of Memory and Language, 2006, 55(3): 335-362.

[10] F Ferreira, J M Henderson. Recovery from misanalyses of garden-path sentences[J]. Journal of Memory and Language, 1991, 30(6): 725-745.

[11] G Hickok. Parallel parsing: Evidence from reactivation in garden-path sentences[J]. Journal of Psycholinguistic Research, 1993, 22(2): 239-250.

[12] E Malaia, R B Wilbur, C Weber-Fox. ERP evidence for telicity effects on syntactic processing in garden-path sentences[J]. Brain and Language, 2009, 108(3):145-158.

[13] J M Novick, E Hussey, S Teubner-Rhodes, et al. Clearing the garden-path: Improving sentence processing through cognitive control training[J]. Language and Cognitive Processes, 2014, 29(2):186-217.

[14] L C Vuong. The role of executive control in garden path reinterpretation[D]. PhD dissertation： RICE University, 2010.

[15] Y Choi, J C Trueswell. Children’s (in)ability to recover from garden paths in a verb-final language: Evidence for developing control in sentence processing[J]. Journal of Experimental Child Psychology, 2010, 106(1):41-61.

[16] 杜家利,于屏方. 花园幽径现象顿悟性的认知解读[J]. 外语与外语教学，2011, (06): 26-29.

[17] M. F. Boston, J. T. Hale. Garden-pathing in a statistical dependency parser[C]//Proceedings of the Midwest Computational Linguistics Conference (MCLC). 2007.

[18] 冯志伟. 花园幽径句的自动分析算法[J].当代语言学, 2003, 5(04): 339-349.

[19] 杜家利,于屏方. 花园幽径现象理解折返性的数据结构分析[J]. 中文信息学报, 2015, 29(1): 28-37.

[20] Y H Jin. Semantic analysis of Chinese garden-path sentences[C]//Proceedings of the Fifth SIGHAN Workshop on Chinese Language Processing, 2006, (7): 33-39.

[21] C J C Lin, T G Bever. Garden path and the comprehension of head-final relative clauses[J]. Processing and Producing Head-final Structures, 2011: 277-297.

[22] N D Patson, F Ferreira. Conceptual plural information is used to guide early parsing decisions: Evidence from garden-path sentences with reciprocal verbs[J]. Journal of memory and language, 2009, 60(4): 464-486.

[23] B McMurray, M K Tanenhaus, R N Aslin. Within-category VOT affects recovery from “lexical” garden-paths: Evidence against phoneme-level inhibition[J]. Journal of Memory and Language, 2009, 60(1): 65-91.

[24] J C Trueswell, M K Tanenhaus, C Kello. Verb-specific constraints in sentence processing: separating effects of lexical preference from garden-paths[J]. Journal of Experimental Psychology: Learning, Memory, and Cognition, 1993, 19(3): 528 -553.

[25] 宋洋, 王厚峰. 共指消解研究方法综述[J]. 中文信息学报, 2015, 29(1):1-12.

[26] 杜家利, 于屏方. 花园幽径句行进错位的计算语言学研究[M].北京: 商务印书馆, 2015.

[27] 杜家利.非对称信息补偿假说: 花园幽径模式的困惑商研究[M].北京: 中国社会科学出版社, 2015.

[28] R W Milne. Predicting garden path sentences[J]. Cognitive Science, 1982, 6(4): 349-373.

[29] E A F Gibson. A computational theory of human linguistic processing: Memory limitations and processing breakdown[D]. School of Computer Science： Carnegie Mellon University, 1991.

[30] M Marcus, G Kim, M A Marcinkiewicz, et al. The Penn Treebank: annotating predicate argument structure[C]//Proceedings of the Workshop on Human Language Technology. Association for Computational Linguistics, 1994: 114-119.

Quantitative Research on the Processing Breakdown in Garden Path: A Computational Linguistic Perspective

DU Jiali1，2, YU Pingfang3

(1.Lexicographical Research Center, Guangdong University of Foreign Studies,Guangzhou, Guangdong 510420, China;2.School of Foreign Studies, Nanjing University, Nanjing, Jiangsu 210093, China;3.Faculty of Chinese Language and Culture, Guangdong University of Foreign Studies,Guangzhou, Guangdong 510420, China)

This article discusses the confusion quotient (CQ) index in the processing breakdown of the garden path phonomenon. The presence of asymmetric information breakdown could lead to spiral upward trend of decoding which showed the pattern of double negation. The amplitude of potential effects of processing breakdown could be measured through the CQ index. Based on large data corpus statistics and online parser analytic method, we calculate the value of CQ index. CQ duration for the preferred construction lies between (-∞, 1], and for the non-preferred construction, [1,2]. The critical values for the preferred and non-preferred structures are 0.72 and 1.28 respectively, and the ambiguous domain lies in [0.72, 1.28]. It is concluded that the frequency deviation of multi-structures is a fundamental reason to lead to different CQ index. The amplitude of processing breakdown and magnitude of asymmetry information compensation are related to CQ index. It is revealed that the statistics-based CQ index can provide the prospective information for decoding the complex structure of local ambiguity.

computational linguistics; garden path model; processing breakdown; local ambiguity; confusion quotient