Numerical Simulations of Heavy Rainfallover Central Korea on 21 Sep tember 2010 Using the WRF M odel

Ui-Yong BYUN,Jinkyu HONG,Song-You HONG,and Hyeyum Hailey SHIN

1Departmentof Atmospheric Sciences,Yonsei University,Seoul,Korea

2Korea Institute of Atmospheric Prediction Systems,Seoul,Korea

3NCAR,Boulder,Colorado,USA

Numerical Simulations of Heavy Rainfallover Central Korea on 21 Sep tember 2010 Using the WRF M odel

Ui-Yong BYUN1,Jinkyu HONG1,Song-You HONG∗2,and Hyeyum Hailey SHIN3

1Departmentof Atmospheric Sciences,Yonsei University,Seoul,Korea

2Korea Institute of Atmospheric Prediction Systems,Seoul,Korea

3NCAR,Boulder,Colorado,USA

On 21 September 2010,heavy rainfall w ith a local maximum of 259 mm d-1occurred near Seoul,South Korea.We examined the ability of the Weather Research and Forecasting(WRF)model in reproducing this disastrous rainfall event and identified the role of two physical processes:planetary boundary layer(PBL)and m icrophysics(MPS)processes.The WRF model was forced by 6-hourly National Centers for Environmental Prediction(NCEP)Final analysis(FNL)data for 36 hours form 1200 UTC 20 to 0000 UTC 22 September 2010.Twenty-five experiments were performed,consisting of five differentPBL schemes—YonseiUniversity(YSU),Mellor-Yamada-Janjic(MYJ),Quasi Normal Scale Elim ination(QNSE), Bougeault and Lacarrere(BouLac),and University of Washington(UW)—and five different MPS schemes—WRF Single-Moment6-class(WSM 6),Goddard,Thompson,M ilbrandt2-moments,and Morrison 2-moments.As expected,there was a specific combination of MPS and PBL schemes thatshowed good skill in forecasting the precipitation.However,there was no specific PBL or MPS scheme thatoutperformed the others in allaspects.The experiments w ith the UW PBL or Thompson MPS scheme showed a relatively small amountof precipitation.Analyses form the sensitivity experiments confi rmed that the spatial distribution of the simulated precipitation was dom inated by the PBL processes,whereas the MPS processes determ ined the amountof rainfall.Itwas also found that the temporalevolution of the precipitation was influenced more by the PBL processes than by the MPS processes.

heavy rainfall,WRF model,m icrophysics,planetary boundary layer

1.Introduction

The Weather Research and Forecasting(WRF)(Skamarock etal.,2008)modelis a mesoscale modeldesigned for both operational applications and atmospheric research.In Korea,the WRF modelhas been w idely used in operational institutions for weather forecasting and academ ic research regarding high-impact weather simulations.The Korea Meteorological Adm inistration(KMA)has operated the Korea WRF(KWRF)since 2005(Cho et al.,2005).Kwun and You(2009)compared the KWRF and the KMA Regional Data Assim ilation and Prediction System(RDAPS)(Lee et al.,2002),the previous operational model,for simulated sea w ind features and typhoon tracks.A lthough both models simulated good results in comparison to the best-track information from the Regional Specialized MeteorologicalCenter (RSMC),the KWRF performed better in predicting typhoon tracks.The Weather Wing of the Korea Air Force(KAF)has operated the weather prediction model system based on the WRF model(i.e.,KAF-WRF)since 2007.The initial and boundary conditions of the KAF-WRF are derived from National Centers for Environmental Prediction(NCEP)Global Forecasting System(GFS)(Moorthi et al.,2001)data and the KAF Global and Regional Integrated Modeling system (GRIMs)(Hong etal.,2013),respectively.The KAF-WRF configuration consists of one-way interactive triple-nested domains(18,6,and 2 km),and each domain covers the East Asian region,the Korean Peninsula,and South Korea.The results of the KAF-WRF are used to supportm ilitary operations that require weather information(Byun etal.,2011).

Several studies have exam ined the effects of various factors—grid size,topography,bogus vortex,data assim ilation,and physics parameterization—in the WRF model configured in East Asia and centered over Korea.Cho and Lee (2006)investigated the effects of grid size on the simulated rainfall distribution,and demonstrated that the WRF model w ith a horizontalgrid size less than or close to 3.3 km should be used for the proper representation of heavy rainfallevents associated w ith multiple convection bands.Jung etal.(2012)examined the effect of topography on heavy snow fall over Yeongdong Province,the mountainous region over the eastern part of South Korea,and showed the importance of orographic forcing w ith a high-resolution mountain datasetin the form of dynam ical circulations associated w ith the snow fall. There have been severalstudies related to the numerical prediction of typhoons in areas of data assimilation(e.g.,Kwon et al.,2010;Lee and Choi,2010).Lee et al.(2010)demonstrated the performance of the Joint Center for High-impact Weather and Climate Research(JHWC)real-time forecast system,which isbased on the WRF model.They showed that the initialdata from the 3-Dimensional Variational(3DVAR) data assimilation using the Global Telecommunication System(GTS),Automatic Weather System(AWS),w ind profi ler,and radar observation data,exhibit improved forecasts in summer rainfallover Korea.

Several studies have investigated the effects of physical parameterizations on the prediction of precipitation.Lee and Park(2002)exam ined the performance of various convective parameterization schemes(CPSs)in the simulation of heavy rainfall over Korea,and found that the dependency on the CPS varies from one case to another.Hong and Lim(2006) showed that,for a high-resolution grid of 5 km,the amount of rainfall and its temporal peak intensity increase as the number of types of hydrometeors used in the m icrophysics (MPS)schemes increases.Shin and Hong(2009)showed that the CPS and Planetary Boundary Layer(PBL)processes significantly change the location of accumulated precipitation, whereas the MPS processes influence the rainfall intensity. These Numerical weather Prediction(NWP)studies examined the effects of a specific parameterization scheme(e.g., one of MPS,CPS,PBL,or Land Surface Model)thatis commonly configured using control and sensitivity experiments and that is different to the scheme in the controlexperiment. It is possible to validate the effects of the target physics parameterization scheme using this configuration.However, this kind of configuration is lim ited in determ ining the general role ofeach physicalprocess because of the complicated interaction between the different parts of the physical processes.

For the above reasons,experiments thatexam ine the role of physicalprocesses using various combinations of physical parameterization schemes have been conducted.Jankov et al.(2007)examined the performance ofan NWP modelover central California w ith combinations of two PBL schemes, four MPS schemes,and two initialization methods.They concluded thatthere is no configuration thatconfi rms the best performance atall times.Evans etal.(2012)investigated the robustness of physical processes for four storm cases over Southeast Australia using 36 simulation results that employ various combinations of physical parameterization schemes including two PBL schemes,two CPS schemes,three MPS schemes,and three radiation schemes,and confi rmed that a specific physics package of the PBL and CPS processes reveals more robust performance than other combinations.A sim ilar conclusion was achieved by Nasrollahietal.(2012)in simulating Hurricane Rita(2005)over the Gulf Coast.These results confi rm that the configurations for the best performance vary depending on the region and targetphenomena. It is also noted that such kinds of experiments using various combinations of physicalparameterization schemes have not been performed for high impact weathers over the Korean Peninsula.

The objective of this study is to exam ine the ability of the WRF model to reproduce the heavy rainfall thatoccurred over Gyeonggi Province on 21 September 2010,w ith a local maximum value of 259 mm in Seoul.The operational forecastby the KMA incorrectly predicted the maximum rainfall amount as approximately 10 to 40 mm d-1over the heavy rainfall region.The influence of the PBL and MPS parameterizations associated w ith the precipitation amounts and the intensity are investigated using the simulated results from the combined experiments of different PBL and MPS parameterization schemes.It is important to note that the main objective of our study is not to judge superiority of a specific combination of two physical processes over others.Rather, our focus is placed on the overall impacts of each PBL and MPS process on the heavy rainfall by exam ining the standard deviations of averaged amounts of precipitation and its localmaxima.Also,the characteristics of a specific scheme overanotherare notpresented since the physical reasoning of a particular scheme for the differences in simulation results has already been given in previous studies based on sensitivity experiments(e.g.,Bright and Mullen,2002;Li and Pu, 2008;Shin and Hong,2009).Section 2 gives an overview of the selected case by analyzing observations,and section 3 describes the experimental setup.The results of the model simulation are discussed in section 4,and concluding remarks are provided in the finalsection.

2.Observationalanalysis

On 21 September 2010,heavy rainfallwas observed over GyeonggiProvince,including Seoul,the capitalcity of South Korea.The local maximum of daily accumulated precipitation was 259 mm in Seoul.Figure 1 shows the observed features of the heavy rainfall.The 36-hraccumulated precipitation regions are extended in the east–west direction over the central region of the Korean Peninsula(Fig.1a).There were peaks in each of the regions(Fig.1b):33.7 mm h-1at0700 UTC 21 September in Seoul,and 9.0 mm h-1at1100 UTC 21 September over the central region of the Korean Peninsula.

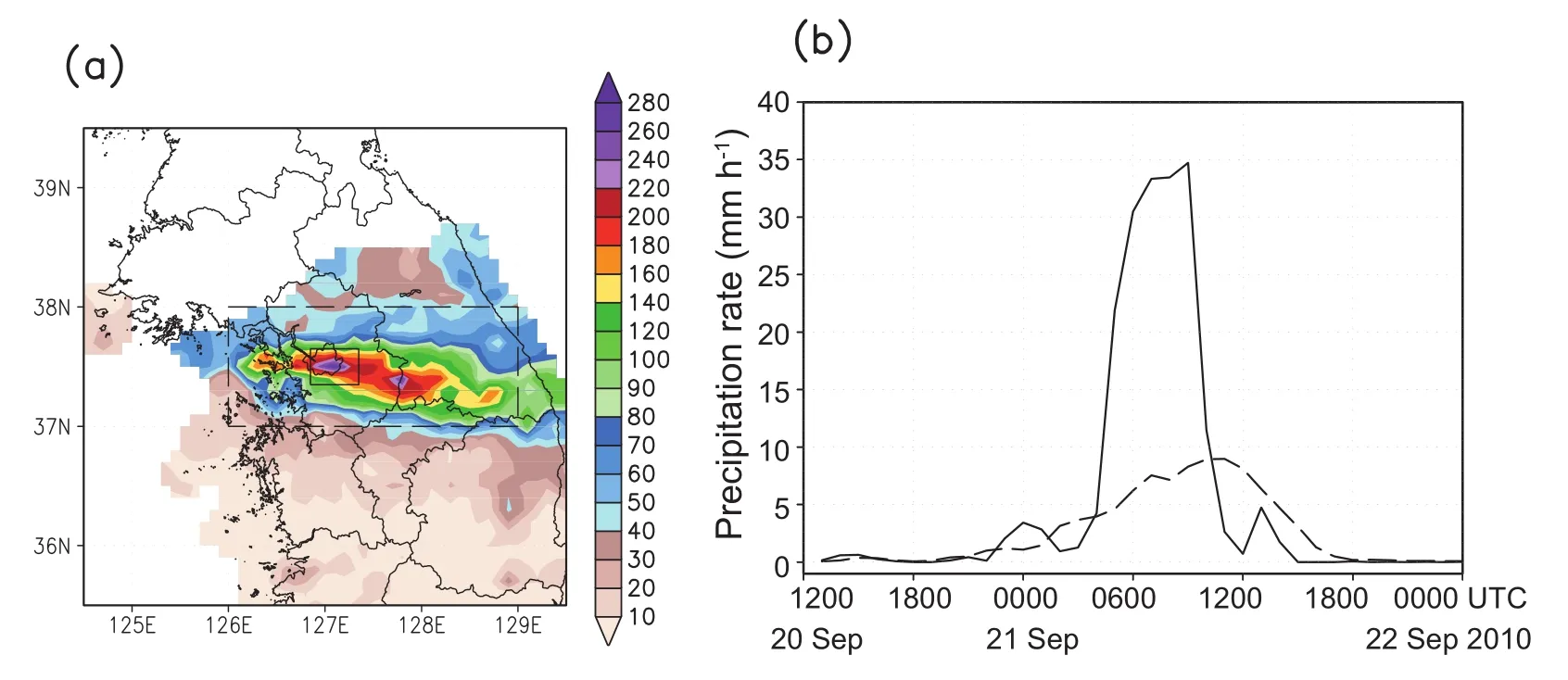
Fig.1.(a)36-h accumulated precipitation(mm)from 1200 UTC 20 to 0000 UTC 22 September 2010 as observed by Korea MeteorologicalAdm inistration(KMA)Automatic Weather System(AWS)stations;(b)hourly time series of the observation from the KMA AWS in the Seoul region[solid box in(a)]and the central region of the Korean Peninsula[dashed box in(a)].

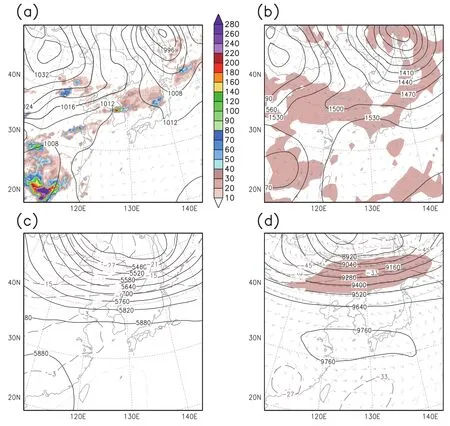
Fig.2.(a)Sea level pressure(hPa)and 10-m w ind vectors(full barb denotes 10 m s-1);(b)850-hPa geopotentialheight(GPH)(m,solid line)and relative humidity over 80%(shaded);(c)500-hPa GPH(m,solid line) and temperature(◦C,dashed line);and(d)300-hPa GPH(m,solid line),temperature(◦C,dashed line),w ind vectors,and isotach over 50 m s-1(shaded)from the National Centers for Environmental Prediction(NCEP) Final Analysis(FNL)data at2100 UTC 20 September2010.The 36-h accumulated precipitation(mm)during the whole event from the Tropical Rainfall Measuring M ission(TRMM)Multi-satellite Precipitation Analysis (TMPA)data is shown in(a).

Figure 2 shows the basic weather charts obtained from the NCEP Final Analysis(FNL)dataset w ith a resolution of 1◦×1◦.At0000 UTC 21 September,a Siberian high in Mongolia expanded to the northern partof the Korean Peninsula, and a northwestern Pacific high pressure system was located over the southern partof the East China Sea(Fig.2a).Convergence of the two air masses provided a favorable synoptic environment for the development of a trough in the central region of the peninsula.This trough appeared only in the layer below 700 hPa.Due to the dissipation of typhoonFanapi(2010),warm and moistairwas advected to southern China(Fig.2b).Associated w ith heavy rainfall over Korea,this air mass was transported to the Korean Peninsula by southwesterly fl ows along the boundary of the northwestern Pacific high.On the 500-hPa and 300-hPa isobaric surfaces(Figs.2c and d),the iso-geopotential line was packed in the north of the Korean Peninsula,and a strong westerly w ind developed.A jetstreak was located in Manchuria in the northern partof the Korean Peninsula.Figure 2a also shows the 36-h accumulated precipitation from the Tropical Rainfall Measuring M ission(TRMM)Multi-satellite Prediction Analysis(TMPA)w ith a resolution of 0.25◦×0.25◦(Huffman etal.,2007).Significant rainfallappeared in the southwestern boundary of the model domain.Intense rainfallwas observed over the central partof the Korean Peninsula.The maximum amount of precipitation over Gyeonggi Province was 239 mm,which was less than that from the AWS data by about20 mm.

The evolution and movement of the convective systems are shown in Fig.3.Around 2100 UTC 20 September,a convective system developed in the eastern partof Shandong peninsula(Fig.3a).This convective cell moved eastward along the trough(Fig.2b)and developed over the Yellow Sea.Three hours later,the convective cell was located near the westcoastof Gyeonggi Province in the Korean Peninsula (Fig.3b).The convective system accompanied the meso low system.After 0300 UTC,the convective cell stagnated over Gyeonggi Province(Figs.3c and d).Moreover,the surface pressure pattern did not change much during thatperiod.At 0600 UTC,the convective cells developed at the location of line formation(Fig.3d).Satellite infrared images indicated that cloud top heights in the convective system were as high as 13 km.The formation and evolution of the mesoscale convective system were analyzed by Jung and Lee(2013).

3.Data and m ethods

3.1.Model description and experimental design

The numerical experiments in this study were executed using version 3.3 of the WRF model.The model consists of one-way interactive triple-nested domains w ith a Lambert conformal map projection.A 3-km domain centered on GyeonggiProvince(Domain 3,160×160)isnested in a 9-km domain(Domain 2,121×121),which in turn is nested in a 27-km domain(Domain 1,142×142)(see Fig.4a).The entire grid system has 31 vertical layers w ith a terrain follow ing coordinate,and the model top is located at 50 hPa.The experiments were performed for36 hours starting at1200 UTC 20 September2010.The initialand 6-hourly lateralboundary conditions were forced by the NCEP FNL data.

The control(CTL)experiment and 25 subsequent sensitivity experiments were executed in order to exam ine the predictability of the heavy rainfalland to demonstrate the roles of the PBL and MPS parameterizations.The setup of the CTL experiment was the same as the KAF-WRF model(Byun et al.,2011),including the WRF Single Moment 6-class (WSM 6)MPS scheme(Hong and Lim,2006),the Kain–Fritsch cumulus parameterization(Kain,2004),a new version of the rapid radiative transfer model(RRTMG)longwave radiation scheme(Iacono et al.,2008),the Goddard shortwave radiation scheme(Tao et al.,2003),the NCEP–Oregon State University–US Air Force–National Weather Service Office ofHydrologic Development(NOAH)land surface model(Chen and Dudhia,2001),and the YonseiUniversity(YSU)PBL scheme(Hong et al.,2006)w ith the new ly implemented treatment of the stable boundary layer(Hong, 2010).Itshould be noted that the cumulus parameterization wasnotused in the 3-km grid domain because of the assumption that the 3-km grid is sufficient to explicitly resolve the convective rainfall.

A llof the sensitivity experiments used the same physical algorithms,except for the different PBL and MPS schemes. The 25 experimentsemployed five differentPBL and five differentMPS schemes.The PBL schemeswere:YSU,Mellor–Yamada–Janjic(MYJ)(Janji´c,1994),Quasi-Normal Scale Elim ination(QNSE)(Sukoriansky et al.,2005),Bougeault and Lacarrere(BouLac)(Bougeault and Lacarr`ere,1989), and University of Washington(UW)(Bretherton and Park, 2009).The MPS schemes were:WSM 6,Goddard(Tao et al.,1989),Thompson(Thompson et al.,2008),M ilbrandt 2-moments(M ilbrandt and Yau,2005),and Morrison 2-moments(Morrison et al.,2009).The five different bulk MPS schemes used in this study can be categorized into single-moment schemes and double-moment schemes.The single-momentschemes—WSM 6 and Goddard—predict the m ixing ratio of the hydrometeors.Meanwhile,the doublemoment schemes—Thompson,M ilbrandt 2-moments,and Morrison 2-moments—predictnotonly the mixing ratio,but also the number concentration of the hydrometeors.In addition,the PBL schemes can also be divided into nonlocal fi rst-order closure schemes(i.e.,YSU)and turbulent kinetic energy(TKE)closure schemes—MYJ,QNSE,BouLac,and UW.The vertical diffusion effect in the TKE scheme can be determined using the local diffusivity of the variable.Meanwhile,both the local diffusivity and the non-localmixing by large convective eddies are required in the nonlocalscheme.

3.2.KMA AWS data

The KMA operates a dense surface AWS observational network in South Korea.Observations began in 1988 w ith only 15 stations,and by 2013 there were 670 stations.The raw data are collected at 1-m in intervals,and the dataset used in this study was archived at 1-h intervals.To evaluate the horizontaldistribution of the amountof precipitation,the horizontally inhomogeneous point values of the AWS data were interpolated onto a 0.1◦grid resolution using the Cressman’s objective analysis scheme(Cressman,1959).The values were averaged w ith weights proportional to the inverse of the squared distance between the center of the grid box and the stations w ithin two radii.One may argue that the skill scores of the simulated precipitation need to be computed on the station grid.We confi rmed that the density of the AWS stations is quite homogeneous,w ith an average distance be-tween them of 13 km,but especially dense over the heavy rainfall region,which did notaffect the computed skillscores over the interpolated grid at0.1◦.

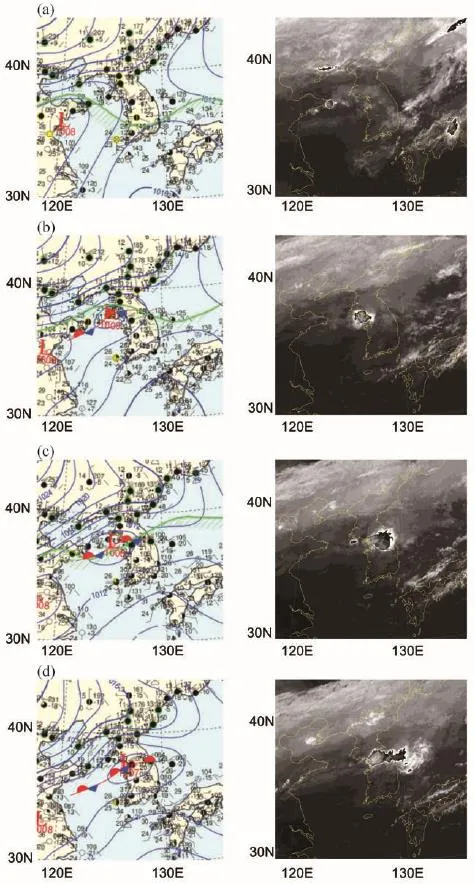
Fig.3.Surface weather charts and enhanced IR imagery at(a)2100 UTC 20,(b)0000 UTC 21(leftpanel),2333 UTC 20(rightpanel),(c)0300 UTC 21,and(d)0600 UTC 21(leftpanel),0533 UTC 21(rightpanel)September 2010.

3.3.Analysis method

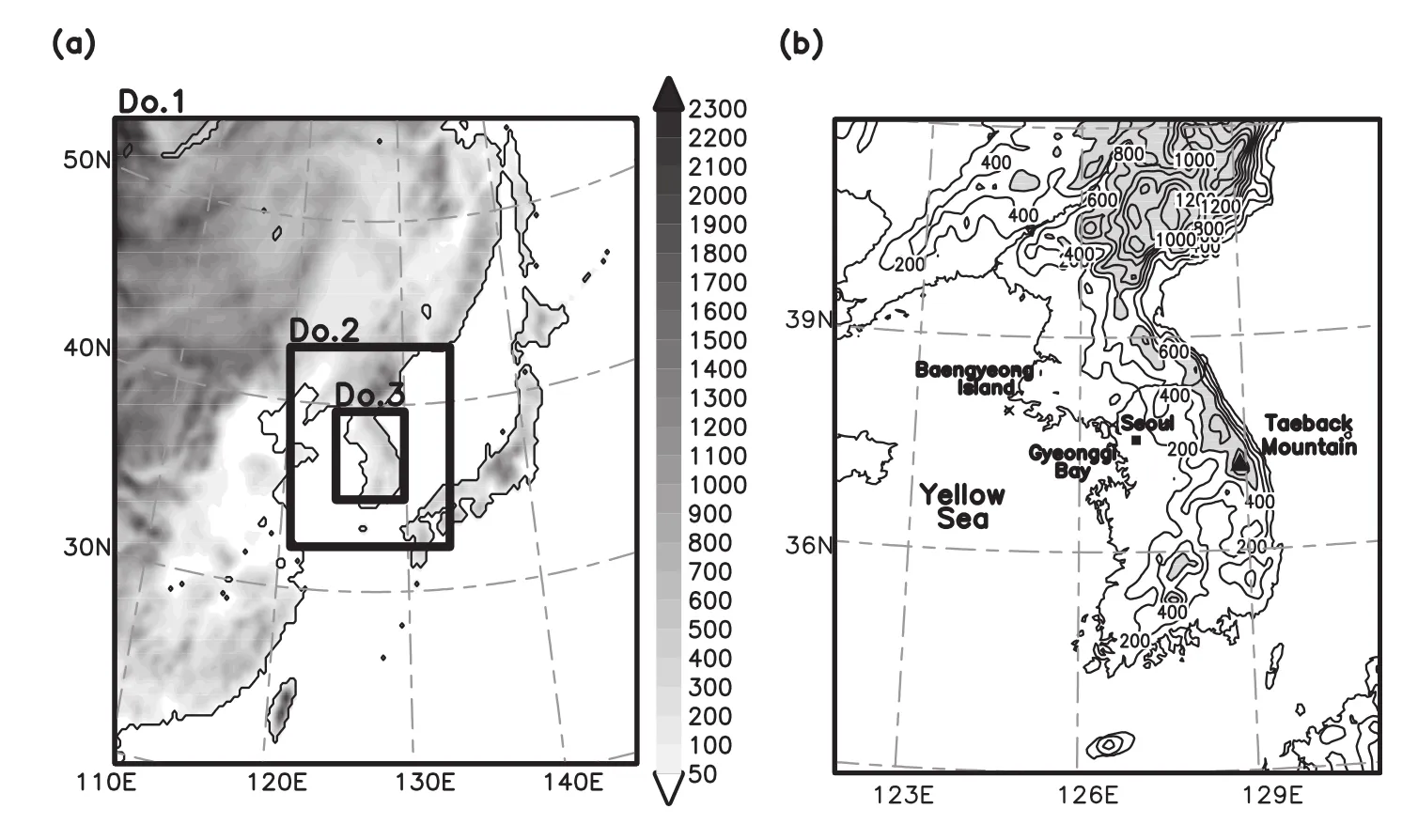
Fig.4.(a)Model domain for the 27-km grid experiment(Domain 1),9-km grid experiment (Domain 2),and 3-km grid experiment(Domain 3)w ith the terrain heights shaded every 100 m.(b)Geographic map of the Korean Peninsula w ith the terrain heights ata 9-km resolution. Contour intervals are 200 m,and values greater than 600 m are shaded.

Forquantitative verification ofeach precipitation sensitivity experiment,the bias,root-mean-square-error(RMSE)and pattern correlation coefficient(PC)between the KMA AWS data and each sensitivity experimentwere calculated at each AWS grid point.For a robustevaluation of intensity,the experimental data were interpolated into a 0.1◦grid resolution by using a 4-point weighting average,w ith the assumption thatAWS data are the bestestimates.The bias is defined as

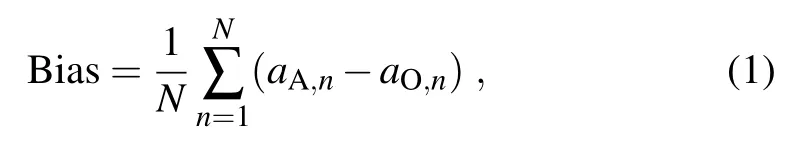
where the summations are performed over allgrid points for the analysis zone,Nis the total number of grid points included in the region,and the superscripts A and O refer to analysis and observations,respectively.The RMSE was also calculated as

The normalized RMSE(NRMSE)isobtained by dividing the RMSE into the observed mean value.The sim ilarity of the horizontal distribution can be objectively measured by the PC,which is expressed as

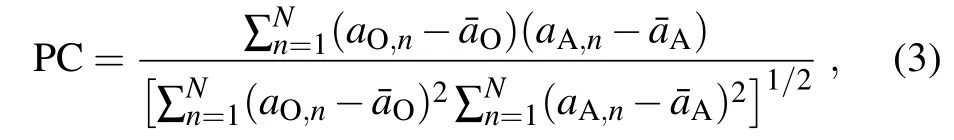
where the bars denote spatialaveraging w ithin a region.

4.Results

4.1.Sensitivity experiments

The CTL experiment simulated the large-scale patterns well,including the Siberian and North Pacific highs and a low pressure system centered over the Sea of Okhotsk(cf., Figs.2a and 5a).Compared w ith the TMPA data in Fig. 2a,the simulated precipitation from the CTL experimentwas similar to whatwas observed in terms of its distribution,but underestimated the local maxima.Over the central Korean Peninsula,the 36-h accumulated precipitation from the CTL run was only 50 mm,which was much less than the 200 mm from the AWS observations.Hereafter,discussion is focused on the results of the 3-km experiments,since the results of the coarse resolution domains were inadequate to resolve mesoscale features.The CTL experimentproperly captured the horizontal distribution of the accumulated rainfall.However,the maximum rainfall amount was approximately 100 mm less than that from observations(cf.,Figs.1a and 5a). The maximum rainfall location was displaced eastward by approximately 30 km compared to the observations.The patterns of accumulated precipitation were separated into Seoul and northern Gyeonggi Province,which is north of Seoul.

Figure 5b shows the time series of the hourly precipitation over the central region of the Korean Peninsula(dashed box in Fig.5a)and the maximum precipitation region(solid box in Fig.5a).In the precipitation time series data thatwere averaged over the central Korean Peninsula region,the rainfall peak appeared 5 hours earlier than the observed peak.The simulated peak of rainfall(9 mm h-1)was sim ilar to the observation in terms ofamount.For the maximum precipitation region,two peaks were produced,unlike the one peak in the observations.The fi rst and second peaks appeared at 0200 UTC and 0500 UTC 21 September,respectively,w ith the second peak occurring 2 hours earlier than thatof the observations.The spurious precipitation was simulated along the Taebaek Mountains,which are located on the eastern flank of the Korean Peninsula,running from north to south.

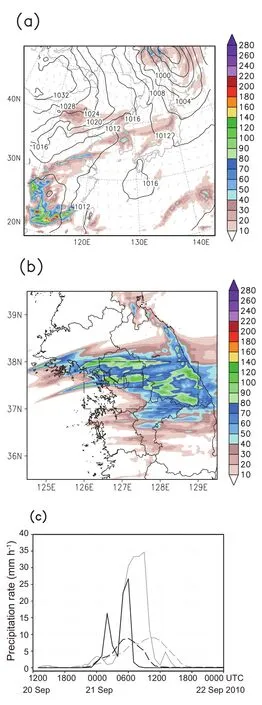
Fig.5.36-h accumulated precipitation(mm)from 1200 UTC 20 to 0000 UTC 22 September 2010 from(a)Domain 1,(b)Domain 3,and(c)hourly precipitation time series from the CTL experiment in the maximum precipitation region[solid box in (b)]and central region of the Korean Peninsula[dashed box in (b)],and the AWS observations(gray line).Sea level pressure (hPa)and 10-m w ind vectors(full barb denotes 10 m s-1)at 2100 UTC 20 September 2010 are shown in(a).

Table 1 shows the bias,RMSE and PC scores for the results from allof the experiments.The objective skillscores for the accumulated precipitation were calculated against the KMA AWS observation data.A more traditionalmeasure of precipitation,such as the threat score,could be used.It is, however,hard to demonstrate the performance of all 25 experiments w ith the threatscore,but the overallevaluation of skillsw ith the scoresin Table 1 was found to comply w ith the skillbased on the threatscore(notshown).Interestingly,particular combinations of the PBL and MPS processes showed betterperformance than othercombinations.The bestcombination in terms of the RMSE and PC scores was observed in the MYJ–M ilbrandtexperiment.The RMSE and PC scores of the MYJ–M ilbrandtexperimentwere 32.33 and 0.75,respectively.The second and third bestscores appeared in the QNSE–Goddard and YSU–Morrison combinations,respectively.The three best combinations did not share the same PBL or MPS scheme,although the YSU PBL showed overall superiorperformance overother PBL schemes foreach MPS scheme.

To verify the variation of the physicalschemes in the skill of precipitation prediction,standard deviations of each skill score were calculated.Ifa scheme had relatively low standard deviation,this meant it had stable performance when combined w ith other physics schemes.The average value of the experiments w ith the YSU PBL scheme for PBL processes showed the lowest RMSE and second lowest standard deviation.The MPS process that demonstrated relatively good performance when combined w ith each of the PBL schemes was the Goddard scheme.The experimentw ith the Goddard MPS scheme combined w ith the QNSE or UW PBL scheme showed the bestRMSE score among the five experiments that employed the same PBL scheme.

Figure 6 presents the 36-h accumulated precipitation and its patterns using various combinations of the PBL and MPS schemes.Each row represents the results for a specific MPS scheme and the different columns show the results w ith the different PBL schemes.Some of the combinations(e.g., MYJ–M ilbrandtand QNSE–Goddard)captured well the distribution of the precipitation band and the maximum precipitation.The results w ith the Goddard scheme showed a higher localmaximum than those from other experiments for the same PBL scheme,except the BouLac–Goddard combinations.The simulations employing the Thompson scheme exhibited a smaller spatial extent of precipitation.The experiments w ith the YSU PBL scheme,except the YSU–Goddard experiment,showed the isolated precipitation over Baengyeong Island(37.95◦N,124.67◦E;see Fig.4b),and along the Taebaeck Mountains,as greater than 90%.The experiments employing the UW scheme tended to exhibita single precipitation band w ith an east–west direction(see Fig. 4b).

4.2.PBL effects

Hereafter,the term“MPS ensemble”denotes an average of the results using the various MPS schemes for a specific PBL scheme,and the term“PBL ensemble”is the average of the results using various PBL schemes for a specific MPSscheme.By comparing the MPS and PBL ensembles and allof the ensemble members,the effects of the physical processes can be confi rmed.

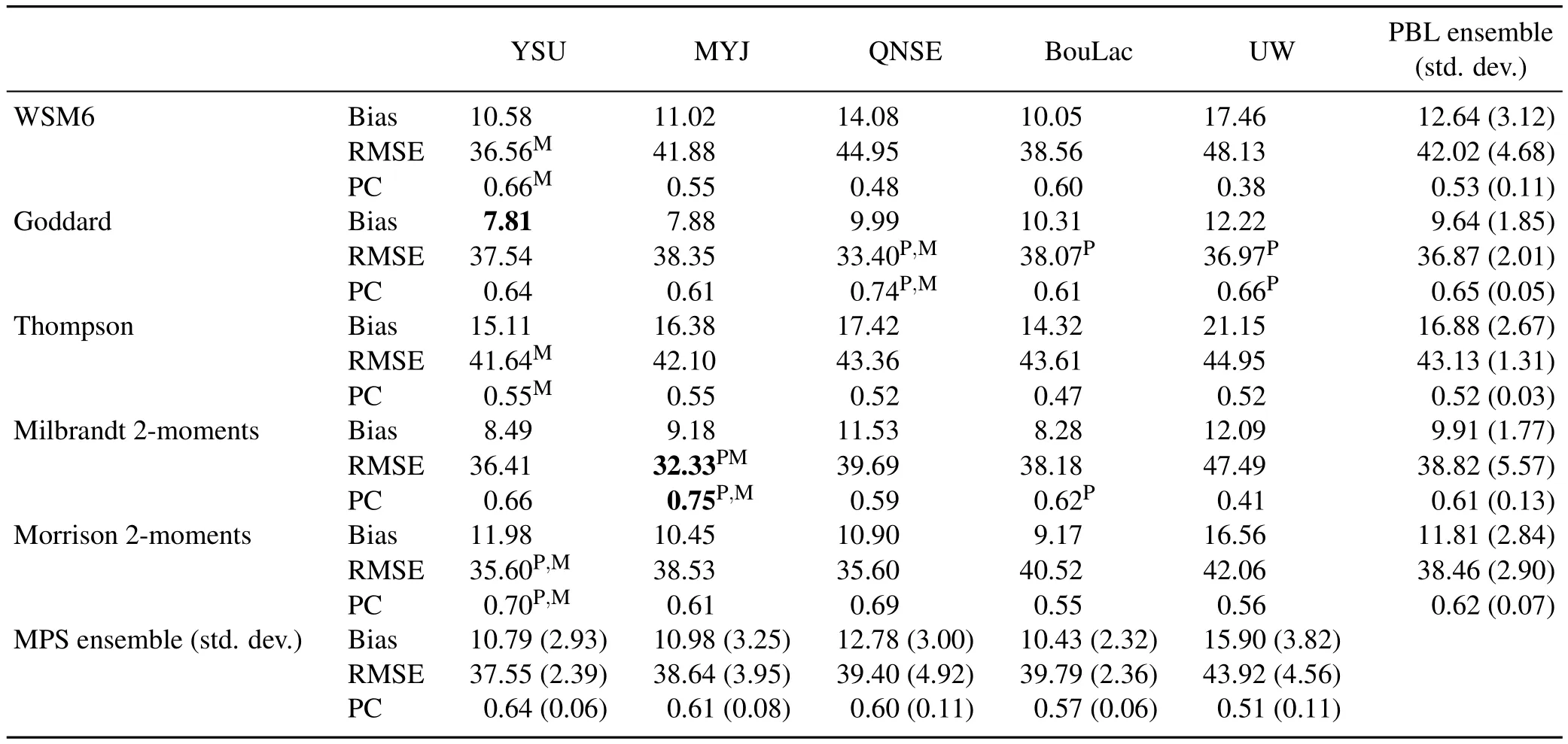
Table 1.The bias,root-mean-square error(RMSE),and pattern correlation(PC)scores averaged over Domain 3 for the 36-h accumulated precipitation(mm).The bestscores among allof the experiments are highlighted in bold.The superscript letters“P”and“M”denote the bestscores of the five experiments thatemployed the same PBL or MPS process,respectively.

In order to determine the distribution of the atmospheric state for each ensemble member,time series of the standard deviations for various variables were calculated.The standard deviations for the sea levelpressure and rainfallover Domain 1 showed sim ilar accuracy between the PBL and MPS ensembles(notshown).However,the standard deviations of the 3-dimensionalvariables appeared differently between the two ensembles(Fig.7).At850 hPa,the standard deviation of the PBL ensemble members had a larger value than that of the MPS ensemble members.The differences between the standard deviations of the MPS ensemble and the PBL ensemble were particularly great w ith regard to the geopotential height and w ind vector.These differences increased over the forecast time.W ith an increase in altitude,the standard deviation of the specific hum idity gradually decreased. This finding indicates that the atmospheric states of the PBL ensemble members were influenced more than those of the MPS ensemble members,especially at loweraltitudes.

Figure 8 presents the hourly precipitation proportion averaged over the lefthalf of the dashed box marked in Fig.1a (Figs.8a and b),and the right half of the same box(Figs. 8c and d).The area of the lefthalf represents the rain band inflow,and the righthalf the dissipating area affected by the orography of the Taebaek Mountains(see Fig.4b).Figure 8 indicates that the precipitation rates varied significantly w ith different combinations of model physics.The time series of the precipitation proportion from the MPS ensemble members showed similar patterns,except for the case of the YSU scheme—shape,hourly proportion,start,peak,and ending time(Fig.8a).The standard deviation ranged below 0.5, except for the YSU result(0.636).When the results from the 25 experiments were sorted by the employed MPS processes,the time series showed higher variability in general. Figure 8b reveals that the standard deviations of the Thompson,M ilbrandtand Morrison schemes were greater than 0.5. This shows that the variability was relatively large when the double-moment MPS schemes(i.e.,Thompson,M ilbrandt, and Morrison)were employed.In the dissipating region,the range of standard deviation for the PBL ensemble(0.430–0.633 mm)was similar to that for the MPS ensemble(0.360–0.694 mm).The experiments w ith relatively higher standard deviations over the inflow area(i.e.,MYJ in the MPS ensemble results;Thompson,M ilbrandt,and Morrison in the PBL ensemble results)showed reduced values over the mountains compared to those over the inflow area,except for the YSU experiment in the MPS ensemble results.Meanwhile,the experiments w ith lower standard deviations over the plain area (i.e.,QNSE,BouLac,and UW in the MPS ensemble results; WSM 6 and Goddard in the PBL ensemble results)showed increased values over the mountains.Overall,the PBL effect on the temporal distribution of the precipitation proportion was more pronounced over the precipitation inflow area than the dissipating region.

The occurrence time of maximum precipitation is shown in the bottom-rightcornerofeach panel in Fig.9.Itisshown that the maximum precipitation occurrence was influenced more by the PBL processes than by the MPS processes.

4.3.MPS effects

Fig.6.36-h accumulated precipitation(mm)from 1200 UTC 20 to 0000 UTC 22 September 2010 for each sensitivity experiment.Contours refer to the 90th percentile of precipitation over 1 mm.The 90th-percentile precipitation value for each experimentis shown in mm in the bottom-rightcornerof each panel.

Table 2.Maximum accumulated precipitation(mm)for36 hours over Domain 3.

Fig.7.Time evolution of the standard deviation for each MPS(black lines)and PBL(gray lines)ensemble member:(a)geopotentialheight(m),(b)temperature(K),(c)specific hum idity(g kg-1),and(d)vectorw ind (m s-1)for the 850-,700-,500-,and 250-hPa pressure levels.

The maximum values of the 36-h accumulated precipitation in each experiment are shown in Table 2.Most experiments simulated the amountof precipitation to be lower than observed(278.60 mm).The simulation w ith the UW– Thompson combination revealed the smallest value(112.91 mm),whereas the QNSE–Goddard combination produced the largest value(374.46 mm).The values of the PBL ensemble ranged from 129.44 mm for the Thompson scheme to 214.40 mm for the Goddard scheme,and the results from the MPS ensemble had a similar range,from 144.81 for the UW to 209.15 for the QNSE scheme.The standard deviation of each ensemble demonstrated the greatest value in ensemble members including the QNSE–Goddard experiment:86.99 mm for the PBL ensemble and 98.49 mm for the MPS ensemble.The PBL ensemble for the Thompson MPS scheme had the loweststandard deviation(17.19 mm)and the second loweststandard deviation appeared in the MPS ensemble for the UW PBL(28.04 mm).

Unlike the maximum precipitation,which was sensitive to both the PBL and the MPS processes,the area-averaged precipitation was influenced more by the MPS than by the PBL processes(Table 3).Compared to the AWS observation (88.70 mm),all the experiments underestimated the amount of precipitation.The experimental results of the PBL ensemble ranged from 47.51 mm for the Thompson scheme to 65.64 mm for the Goddard scheme.This range was greater than that of the MPS ensemble,which ranged from 52.84 mm for the UW scheme to 63.60 mm for the MYJ scheme.The standard deviations of the PBL and MPS ensembles differed significantly.The standard deviation of the PBL ensemble forthe Thomson scheme was only 1.93 mm.The largest standard deviation value of the PBL ensemble(6.11 mm)was relatively small,as compared to the MPS ensemble,ranging from 6.03 to 9.54 mm.Each member of the PBL ensemble simulated sim ilar total rainfallamounts.It is thus concluded thatthe maximum rainfallamountshould be equally sensitive to the MPS and PBL processes,while the average amount is more sensitive to the MPS than the PBL processes.

Table 3.The 36-h accumulated precipitation(mm)averaged over the area marked by the dashed box in Fig.1a.

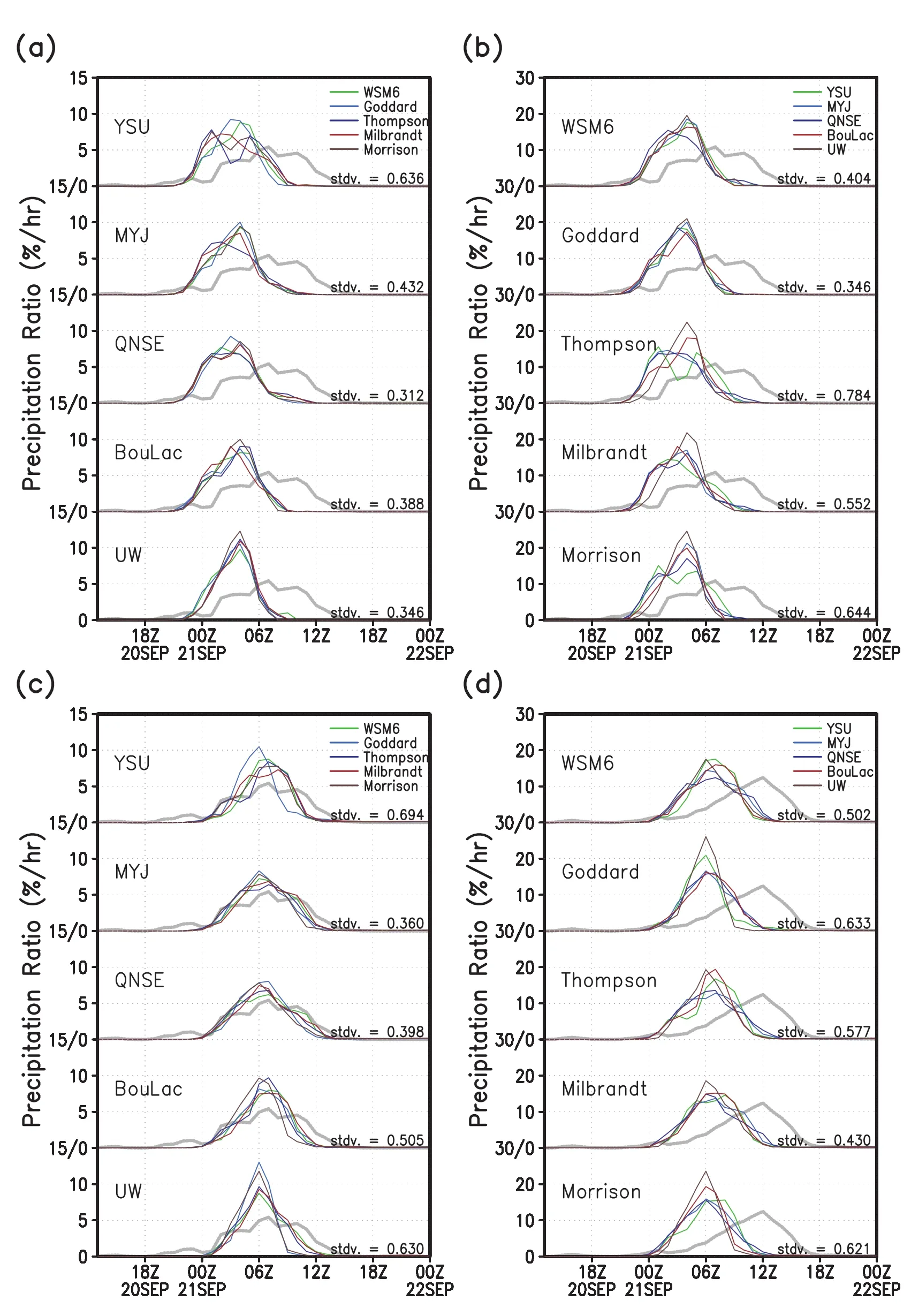
Fig.8.Time series of the simulated precipitation proportion averaged over the(a,b)lefthalf of the dashed box marked in Fig.1a(37◦–38◦N,126◦–127.5◦E)and(c,d)righthalf(37◦–38◦N,127.5◦–129◦E),and the AWS observations(gray dotted line).The 25 experiments are sorted by the selected physicalprocesses:(a,c)PBL; (b,d)MPS.

Fig.9.Verticaldistributions of water species,averaged for 2 h at the valid time,which is the maximum precipitation over the heavy rainfall region marked as a dashed box in Fig.1a.The valid time for the maximum of 1-h accumulated precipitation is shown in the bottom-rightcorner of each panel.

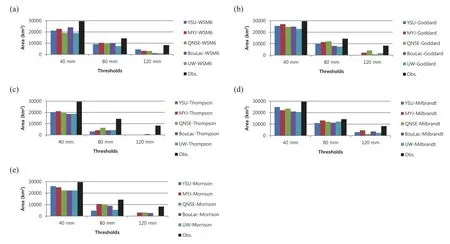
Fig.10.Areal extent of the simulated 36-h accumulated precipitation over the area marked as a dashed box in Fig.1a for the PBL ensemble members w ith the(a)WSM 6,(b)Goddard,(c)Thompson,(d)M ilbrandt 2-moments,and(e)Morrison 2-moments MPS schemes.

The areal extent of precipitation was calculated as the productof the numberofgrid points thatexceeded a specified rainfall threshold and grid size.Figure 10 indicates the areal extent computed at three thresholds(40,80,and 120 mm). A llof the experiments underestimated the arealextent for the three thresholds.The MYJ–Goddard combination showed the leasterror in the 40-mm threshold.In the 80-and 120-mm thresholds,the MYJ–M ilbrandtcombination showed the least error.The precipitation area was sim ilarly simulated when the same MPS was employed.The Goddard scheme showed a betteraverage performance in the 40-mm threshold, and the M ilbrandtscheme showed better performance in the 80-and 120-mm thresholds.Overall,the Thomson scheme underestimated the area for allof the thresholds.

The reason for these characteristics—average precipitation,and precipitation areal extent—which depend on the MPS scheme employed,comes from the difference in the simulated water species in each experiment.In order to confi rm the simulated water species characteristics,the vertical profi les of the area’s averaged condensates were obtained from each experimentand the results are plotted in Fig.9. The experiments thatemployed the same MPS scheme produced sim ilarprofi les forwaterspecies,especially for the ice phases such as ice,snow and graupel.The Thompson experiments,which simulated weak precipitation rate,showed a smaller maximum rainwater mixing ratio(average:0.25 g kg-1),and the Goddard experiments,which simulated a relatively strong precipitation rate,showed larger values(average:0.46 g kg-1)than the other MPS experiment results (between 0.32 and 0.39 g kg-1).The difference in the rainwater m ixing ratio between the sensitivity experiments,the reason for the difference in the rainfall amount,was influenced by the ice phase mixing ratio.There were few ice and graupel particles above the 4 km height in the Thompson scheme results;however,the Goddard and M ilbrandt schemes,which simulated a large amount of precipitation, both showed higher maximum mixing ratios of graupel(between 0.50 and 0.87 g kg-1)ata heightof6 km.The Goddard scheme showed a maximum snow m ixing ratio at 9 km,and the M ilbrandtscheme a maximum ice mixing ratio at12 km.

5.Concluding remarks

In this study,we exam ined the capability of the WRF model to simulate the heavy rainfall event over Gyeonggi Province on 21 September 2010.The local maximum of observed precipitation was approximately 259 mm d-1.A triple-nested WRF model w ith a highest resolution of 3 km was forced by 6-hourly NCEP FNL data for 36 hours from 1200 UTC 20 to 0000 UTC 22 September 2010.A total of 25 experiments w ith five different PBL schemes—YSU,MYJ,QNSE,BouLac,and UW—and five different MPS schemes—WSM 6,Goddard,Thompson,M ilbrandt 2-moments,and Morrison 2-moments—were conducted in order to investigate the role of the PBL and MPS processes in simulating the heavy rainfall.

The WRF model simulated the spatial distribution of the 36-h accumulated precipitation reasonably well,show ing it extending from the west coast of the Korean Peninsula eastward,although its maximum was underestimated.Sensitivity experiments revealed that a particular combination of the PBL and MPS processes resulted in relatively good performance:the MYJ–M ilbrandt,QNSE–Goddard,and YSU–Morrison schemes for the PBL and MPS processes,respectively.This conclusion refl ects previous fi ndings thatdemon-strated good skill in reproducing high-impact weathers by a particular combination of physics packages,w ith no specific scheme outperform ing in allaspects,although the YSU scheme for the PBL and Goddard scheme for the MPS processes revealed relatively good skill in the forecastof the selected heavy rainfall.

A major focusof thisstudy was the relative importance of the PBL and MPS processes in simulating the distribution of accumulated precipitation,its local maximum,and temporal evolution of the precipitation over the heavy rainfall region. These issues were addressed by exam ination of the ensemble spread of skill scores from the experiments w ith particular PBL or MPS schemes.It was found that the PBL process affected the onsetof the rainfall in the heavy rainfall region, and its dissipation.A lso,the areal distribution of the precipitation over the heavy precipitation region was influenced more by the PBL processes than by the MPS processes.This relative importance of the PBL processes was found to be due to the modulated atmospheric structure in the lower troposphere.Shin and Hong(2011)revealed that the stability at lower levels is significantly affected by PBL processes,which may affect the temporalevolution of simulated precipitation and its arealdistribution.Meanwhile,the amountof precipitation was influenced more by the MPS than by the PBL processes.Whereas the maximum precipitation was sensitive to both the PBL and MPS processes,the amountof areaaveraged precipitation was influenced more by the MPS than by the PBL processes.

It is important to note that the conclusion of this study is lim ited,mainly due to the fact that we have exam ined a single case study only.The relative importance of PBL and MPS processes may depend upon the characteristics of the selected heavy rainfall case.The selected convective system was thermodynam ically organized by local instability,and further studies w ith different mechanisms,such as synoptically organized systems,is needed.Despite this uncertainty, our findings contribute to identifying the key algorithm for improving the forecastskillofheavy rainfallover EastAsia.

Acknow ledgements.This work was carried out through an R&D projecton the development of globalnumericalweather prediction systems at the Korea Institute of Atmospheric Prediction Systems(KIAPS)and under Grant CATER 2012-3035 funded by the Korea Meteorological Administration(KMA).

REFERENCES

Bougeault,P.,and P.Lacarr`ere,1989: Parameterization of orography-induced turbulence in a mesobeta-scale model. Mon.Wea.Rev.,117,1872–1890.

Bretherton,C.S.,and S.Park,2009:A new moist turbulence parameterization in the Community Atmosphere Model.J.Climate,22,3422–3448.

Bright,D.R.,and S.L.Mullen,2002:The sensitivity of the numericalsimulation of the southwestmonsoon boundary layer to the choice of PBL turbulence parameterization in MM 5. Wea.Forecasting,17,99–114.

Byun,U.Y.,and Coauthors,2011:WRF-based short-range forecastsystem of the Korea Air Force:Verification of prediction skill in 2009 summer.Atmosphere,21,197–208.(in Korean w ith English abstract)

Chen,F.,and J.Dudhia,2001:Coupling an advanced land surfacehydrology modelw ith the Penn State-NCAR MM 5 modeling system.Part I:Model implementation and sensitivity.Mon. Wea.Rev.,129,569–585.

Cho,I.-H.,H.-D.Yoo,and J.-O.Lim,2005:Korea Weather Research and Forecasting(KWRF)construction and test operating.Proceedings of the 2005 Fall Meeting of Korea Meteorological Society,Gangneung,Korea,Korean Meteorological Society,233–234.

Cho,N.-S.,and T.-Y.Lee,2006:A numerical study of multiple convection bands over the Korean peninsula.J.Korean Meteor.Soc.,42,87–105.

Cressman,G.P.,1959:An operational objective analysis system. Mon.Wea.Rev.,87,367–374.

Evans,J.P.,M.Ekstrom,and F.Ji,2012:Evaluating the performance ofa WRF physics ensemble over South-EastAustralia. Climate Dyn.,39,1241–1258.

Hong,S.-Y.,2010:A new stable boundary-layer mixing scheme and its impacton the simulated EastAsian summermonsoon. Quart.J.Roy.Meteor.Soc.,136,1481–1496.

Hong,S.-Y.,and J.-O.J.Lim,2006:The WRF Single-Moment6-Class m icrophysics scheme(WSM 6).J.Korean Meteor.Soc., 42,129–151.

Hong,S.-Y.,Y.Noh,and J.Dudhia,2006:A new verticaldiffusion package w ith an explicit treatmentof entrainmentprocesses. Mon.Wea.Rev.,134,2318–2341.

Hong,S.-Y.,and Coauthors,2013:A multi-scale atmospheric/ ocean modeling system:The Global/Regional Integrated Model system(GRIMs).Asia-Pacific J.Atmos.Sci.,49(2), 219–243.

Huffman,G.J.,and Coauthors,2007:The TRMM Multisatellite Precipitation Analysis(TMPA):Quasi-global,multiyear, combined-sensor precipitation estimates at fine scales.J.Hydrometeor.,8,38–55.

Iacono,M.J.,J.S.Delamere,E.J.M lawer,M.W.Shephard,S. A.Clough,and W.D.Collins,2008:Radiative forcing by long-lived greenhouse gases:Calculations w ith the AER radiative transfer models.J.Geophys.Res.,113,D13103,doi: 10.1029/2008JD009944.

Janji´c Z.I.,1994:The step-mountain eta coordinate model—Further developments of the convection,viscous sublayer, and turbulence closure schemes.Mon.Wea.Rev.,122,927–945.

Jankov,I.,P.J.Schultz,C.J.Anderson,and S.E.Koch,2007:The impactof differentphysicalparameterizations and their interactions on cold season QPF in the American River basin.J. Hydrometeorol.,8,1141–1151.

Jung,S.-H.,E.-S.Im,and S.-O.Han,2012:The effect of topography and sea surface temperature on heavy snow fall in the Yeongdong region:A case study w ith high resolution WRF simulation.Asia-Pacific J.Atmos.Sci.,48,259–273.

Jung,W.,and T.-Y.Lee,2013:Formation and evolution of mesoscale convective systems thatbrought the heavy rainfall over Seoulon September21,2010.Asia-Pacific J.Atmos.Sci., 49,635–647.

Kain,J.S.,2004:The Kain-Fritsch convective parameterization: An update.J.Appl.Meteor.,43,170–181.

Kwon,I.-H.,H.-B.Cheong,H.-G.Kang,H.-J.Han,and J.-R.Park,2010:Structure change of Typhoon Nari(2007)in the weakening stage.Asia-Pacific J.Atmos.Sci.,46,327–340.

Kwun,J.H.,and S.H.You,2009:Numerical study of sea w inds simulated by the high-resolution Weather Research and Forecasting(WRF)model.Asia-Pacific J.Atmos.Sci.,45,523–554.

Lee,D.-K.,and J.-G.Park,2002:A comparison study of moist physics schemes in simulation of EastAsian heavy rainfall.J. Korean Meteor.Soc.,38,581–592.

Lee,D.-K.,and S.-J.Choi,2010:Observation and numericalprediction of torrential rainfall over Korea caused by Typhoon Rusa(2002).J.Geophys.Res.,115,D12105,doi:10.1029/ 2009JD012581.

Lee,D.-K.,D.-Y.Eom,J.-W.Kim,and J.-B.Lee,2010:Highresolution summer rainfall prediction in the JHWC real-time WRF system.Asia-Pacific J.Atmos.Sci.,46,341–353.

Lee,M.-S.,W.-J.Lee,and K.-H.Youn,2002:Origin of cold bias in KMA RDAPS-2000 and its improvements in 2001.Atmosphere,12,336–339.

Li,X.L.,and Z.X.Pu,2008:Sensitivity of numerical simulation of early rapid intensification of Hurricane Em ily(2005) to cloud microphysicaland planetary boundary layer parameterizations.Mon.Wea.Rev.,136,4819–4838.

M ilbrandt,J.A.,and M.K.Yau,2005:A multimoment bulk microphysics parameterization.Part II:A proposed threemoment closure and scheme description.J.Atmos.Sci.,62, 3065–3081.

Moorthi,S.,H.-L.Pan,and P.Caplan,2001:Changes to the 2001 NCEP operational MRF/AVN global analysis/forecast system.NWS Tech.Procedures Bulletin 484,14 pp.[Available online athttp://www.nws.noaa.gov/om/tpb/484.htm.]

Morrison,H.,G.Thompson,and V.Tatarskii,2009:Impact of cloud microphysics on the developmentof trailing stratiform precipitation in a simulated squall line:Comparison of oneand two-momentschemes.Mon.Wea.Rev.,137,991–1007.

Nasrollahi,N.,A.AghaKouchak,J.L.Li,X.G.Gao,K.L.Hsu, and S.Sorooshian,2012:Assessing the impacts of differentWRF precipitation physics in hurricane simulations.Wea. Forecasting,27,1003–1016.

Shin,H.,and S.-Y.Hong,2009:Quantitative precipitation forecast experiments of heavy rainfall over Jeju Island on 14–16 September2007 using the WRF model.Asia-Pacific J.Atmos. Sci.,45,71–89.

Shin,H.,and S.Y.Hong,2011:Intercomparison of planetary boundary-layer parameterizations in the WRF model for a single day from CASES-99.Bound.-Layer Meteor.,139,261–281.

Skamarock,W.C.,and Coauthors,2008:A description of the advanced research WRF Version 3.NCAR/TN-475+STR,doi: 10.5065/D68S4MVH.

Sukoriansky,S.,B.Galperin,and V.Perov,2005:Application of a new spectral theory ofstably stratified turbulence to the atmospheric boundary layer over sea ice.Bound.-Layer Meteor., 117,231–257.

Tao,W.-K.,J.Simpson,and M.M cCumber,1989:An ice-water saturation adjustment.Mon.Wea.Rev.,117,231–235.

Tao,W.-K.,and Coauthors,2003:M icrophysics,radiation and surface processes in the Goddard Cumulus Ensemble(GCE) model.Meteor.Atmos.Phys.,82,97–137.

Thompson,G.,P.R.Field,R.M.Rasmussen,and W.D.Hall, 2008:Explicit forecasts of w inter precipitation using an improved bulk m icrophysics scheme.Part II:Implementation of a new snow parameterization.Mon.Wea.Rev.,136,5095–5115.

:Byun,U.-Y.,J.Hong,S.-Y.Hong,and H.H.Shin,2015:Numerical simulations of heavy rainfall over central Korea on 21 September2010 using the WRF model.Adv.Atmos.Sci.,32(6),855–869,

10.1007/s00376-014-4075-6.

(Received 7 April2014;revised 14 August2014;accepted 5 September2014)

∗Corresponding author:Song-You HONG

Email:songyouhong@gmail.com

©Institute of Atm ospheric Physics/Chinese Academ y of Sciences,and Science Press and Springer-Verlag Berlin Heidelberg 2015