一种基于FRFT的标量脱靶量测量方法
2015-04-20陶坤宇
陈 龙, 王 丽, 陶坤宇
(上海无线电设备研究所,上海200090)
0 引言
在导弹打靶试验中,脱靶量的测量对鉴定和评估导弹性能起着重要的作用。当前脱靶量测量中应用较多的是基于弹目交会段多普勒频率变化率的无线电测量方法。由于弹目交会段多普勒频率的时变特性以及近场体目标效应的影响,使得多普勒频谱被展宽,从而降低了脱靶量的估计精度。因此,在弹目交会过程中,根据目标回波信号的特点,针对FFT 方法估计多普勒频率的不足,本文采用分数阶傅里叶变换的方式测量多普勒频率,提高了测量精度。
1 标量脱靶量的多普勒测量原理
假设无线电脱靶量测量设备安装于靶标上,导弹相对靶标作匀速直线运动,导弹运动轨迹与靶标相距最近的点到靶标的距离即为待测的脱靶量。在弹目共面遭遇时,以某时刻导弹的位置为基准点,且设定为坐标原点。导弹与靶标连线方向为x 轴,垂直该连线方向为y 轴,如图1所示。在弹目交会阶段,导弹A 相对靶机B以匀速vr飞行。记基准点时刻t=0。在t0时刻,导弹与靶标交会于M 点,即当t=t0时,导弹处于脱靶点位置(M 点),其与靶标间的距离最短,此时多普勒频率fD(t0)=0。

图1 导弹-靶机交会示意图
在弹目交会段,实时多普勒频率为
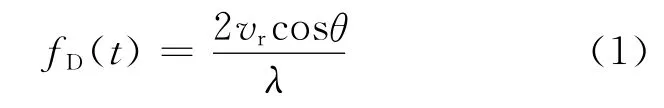
式中:vr导弹相对靶标的速度;θ为相对速度矢量与弹目连线的夹角;λ为载波波长。
由图1知

式中:t0为从基准点运动到遭遇点的时间;t为从基准点起的任意时刻;ρ 为脱靶量。多普勒频率为

式中:ρ为脱靶量。设λ=18.75mm;脱靶量分别为0.5,2,4,6,8,10m;相对速度vr分别为200,600,1 000m/s,1 500m/s;坐标原点为脱靶点前0.15s处,即t0=0.15s。根据式(3),得到不同脱靶量、不同速度情况下的多普勒频率变化情况如图2所示。
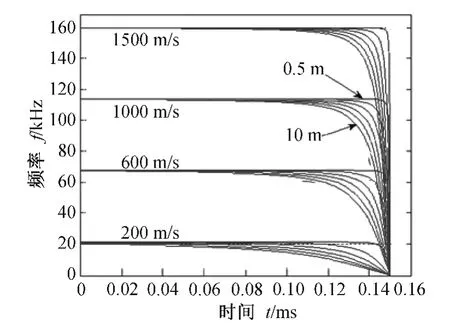
图2 不同速度、不同脱靶量情况下的多普勒频率
从图2中可看出,不同弹目相对速度及脱靶量情况下,回波多普勒信号的初始频率和频率变化率有较大差异。弹目相对速度越大,回波多普勒信号的初始频率越高;相对速度相同时,回波多普勒信号的起始频率相同,且脱靶量越小,交会时间越短,多普勒频率的变化率越大。
由式(3)可知,弹目交会时,在相对速度vr一定的情况下,弹目多普勒曲线的变化仅与脱靶量ρ有关。也就是说,在距脱靶点同一个时刻(t0-t),不同的脱靶量ρ对应的多普勒频率fD各不相同。当已知相对速度、工作波长的情况下,测量运动过程中任意两个不同时刻对应的多普勒频率,即可求解交会时刻t0及脱靶量ρ。
选取t1=t(i)及t2=t(j)两个时刻的采样数据,代入式(3),得方程组为:
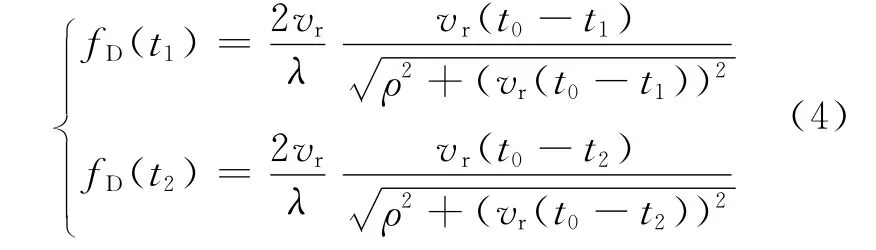
即
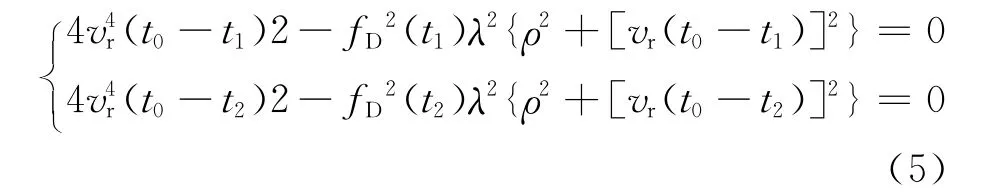
令

由牛顿迭代法,可得

其中:


在弹目交会全过程中,为消除随机误差的影响,对连续测量多普勒信号频率求解的脱靶量取平均,可以进一步提高脱靶量估计精度。
2 基于FRFT 的多普勒频率估计
在弹目交会阶段的多普勒信号可以近似为一段LFM 信号,分数阶傅里叶变换是一种广义的傅里叶变换,其核函数为

改变角度α,可对应不同的分数阶傅里叶变换的基。当LFM 信号的调频率与某一分数阶傅里叶变换基的调频率吻合,信号的分数阶傅里叶变换就在该变换基上成为一个冲激函数。
假设多普勒信号时域表达式为

式中:f0为被分析时间段内信号的中心频率;k为调频斜率;T 为调制周期。
假设系统采样频率为fs,采样点数为N,FRFT 阶数为p,以p 为变量,对LFM 信号进行FRFT,形成(p,u)平面,其中p 从0 到4 满足FRFT 的一个周期,在此二维平面上进行搜索,得到LFM 信号FRFT 域功率峰值相对应的位置(p0),p0即为FRFT 分析的最佳阶数。最佳FRFT 旋转角度α0=πp0/2。
根据FRFT 峰值位置(p0)可得中心频率f0及调频斜率k的估计值:

设弹目相对速度vr=1 500m/s,脱靶量ρ=5 m,在采样频率fs=1 MHz的条件下,在交会段脱靶点前10ms时间内进行仿真。多普勒时域信号、FFT 功率谱和FRFT 功率谱分别如图3、图4和图5所示。
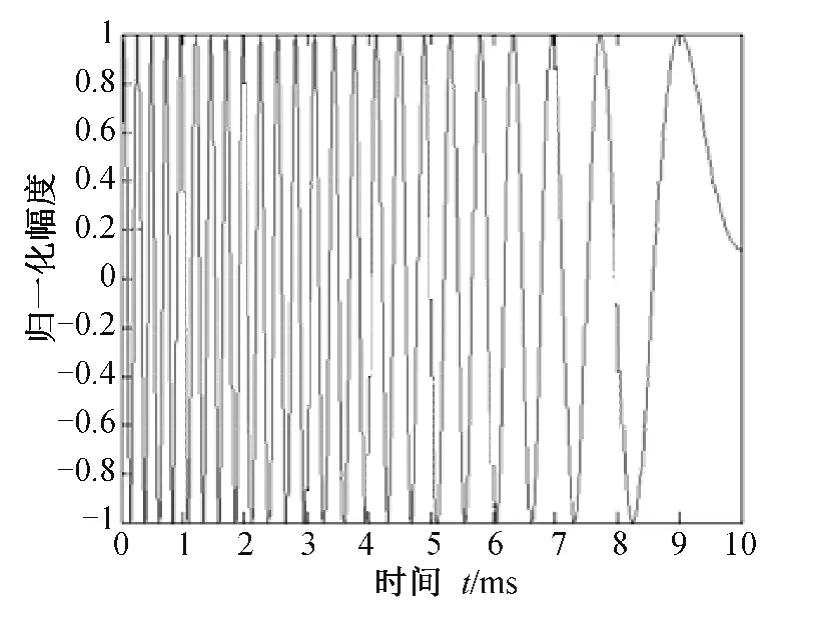
图3 多普勒时域信号

图4 FFT 功率谱

图5 FRFT 功率谱
仿真结果表明,交会段多普勒信号经过FRFT 变换后,窄带调频频谱在频率轴上出现能量聚集,在某一频点出现最大值,其谱线类似于点频谱线。相对于FFT,FRFT 能够更可靠的检测,并计算出中心频率,为下一步计算脱靶量提供准确参考。另外,为验证FRFT 频率估计的有效性,选取多组多普勒时域信号分别作FFT 和FRFT 运算,获得的多普勒频率如表1 所示。由表可见FRFT 具有更高的频率估计精度。

表1 FFT及FRFT频率估计结果对照表
表中:fD为理伦值;^fD为估计值;绝对误差为Δf=^fD-fD,相对误差Δf/fD。
3 基于FRFT 的脱靶量仿真
假设系统工作频率f0=16GHz,即工作波长λ=0.018 75m,测量系统采样频率fs=1 MHz,信噪比SNR=10dB,则经过FRFT 后的多普勒频率估计结果与理论多普勒频率对比如图6所示。
在vr=(200~1 500)m/s,ρ=(0.5~10)m范围内分别进行仿真验证,其结果如表2所示。
4 结论
本文提出了基于分数阶傅里叶变换(FRFT)的目标回波多普勒频率估计算法,并根据牛顿迭代法估计标量脱靶量,通过仿真分析,证明本算法相对普通FFT 算法,具有更高的估计精度。
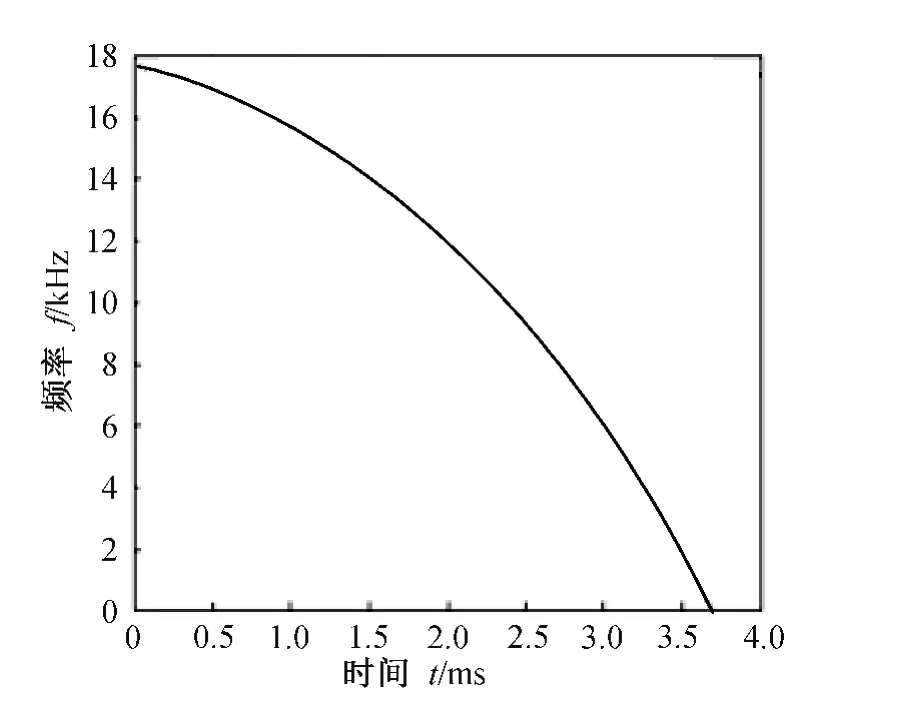
图6 FRFT 频率估计结果与理论多普勒频率对比图

表2 FRFT脱靶量估计结果
[1] 陶然,邓兵,王越.分数阶傅里叶变换及其应用[M].北京:清华大学出版社,2009.
[2] 李兴民,周敬国.导弹脱靶量测量方法研究[J].战术导弹技术,2004,(2):22-25.
[3] 赵兴浩,邓兵,陶然.分数阶傅里叶变换数值计算中的量纲归一化[J].北京理工大学学报,2005,25(4):360-364.
[4] 张雯雯,刘黎平.一种简化的分数阶傅里叶变换及其应用[J].数据采集与处理,2009,24(6):814-818.
