机械应力对石英滤波输出的影响

高 傲，夏 刚，孔 勇，刁 利，王文龙，韩 华

(上海工程技术大学电子电气学院，上海201620)

引 言

光学滤光片是重要的无源器件之一，能按照需要来改变入射光的光谱强度分布，是在连续光谱中透过一定宽度的光谱带或在线状光谱中用来提取某些辐射的波长选择器件［1］。光学滤光片早期用于天文观测，随着激光技术的发展，光学滤光片在激光滤波、光传感、光谱分析和光纤通信［2-6］等领域起着重要作用。

光学滤光片种类很多，根据不同原理可分为选择吸收滤波器、多光束干涉滤波器、色散滤波器、双折射滤波器［7-8］等等。双折射滤光片具有结构简单、滤波频带宽、滤波波形可精确调节、可实现0.1nm级的滤波线宽等优点，在太阳光谱研究、激光腔内波长选择器、波分复用(wavelength division multiplexing，WDM)器件、光纤增益均衡器件等领域中有广泛的应用。石英晶体由于其二向色性小、使用波段宽(185nm～3500nm)、机械强度好、人工生长技术成熟、易于得到大块的光学级晶体等特点，成为重要的双折射材料。石英晶体滤光片在组装和器件封装时易受机械振动的影响，从而中心波长发生漂移，影响其滤光效果，因此，研究机械应力对石英晶体滤光片的影响，对正确设计及使用双折射滤光片具有重要意义。

机械应力对石英滤波输出的影响国内还鲜见报道，作者主要研究机械应力对Lyot型石英滤光输出的影响，基于石英晶体的弹光效应，推导出了石英晶体双折射率与不同方向机械应力的关系，进行了理论上的模拟。根据Lyot型滤光片原理，利用Ultra-6600系列紫外-可见分光光度计设计实验进行验证。理论模拟和实验结果有很好的一致性，机械应力作用下石英滤光片中心波长发生漂移。

1 基本原理

1.1 Lyot型滤光片的原理

典型的Lyot型滤光片通常由几个双折射器件和数个偏振器件组成，单级Lyot型滤光片结构如图1所示［7，9］。

Fig.1 Schematic diagram of a unipolar Loyt filter

图中，P1和P2是偏振镜，S是平行光轴平行于晶体表面的石英晶片，两偏振镜P1和P2的偏振面相互平行，S的光轴方向与两偏振镜P1和 P2偏振面成45°，o光和e光的相位延迟量δ为:

式中，λ为入射光波长，Δn为折射率差，d为石英晶片的厚度。

根据偏振干涉理论，可得单级Lyot滤光片的透射率T是偏振双折射器件所产生相位延迟量δ的函数:

1.2 石英晶体在机械应力作用下折射率差的变化

下面从理论方面讨论机械应力作用下石英晶体弹光效应引起的入射光折射率差的变化，石英晶体属于三方晶系的晶类，晶轴方向为Ox1，Ox2，Ox3，3个方向的应力分别为 σ1，σ2，σ3。

(1)假设有平行于光轴Ox3的单向正应力σ作用于石英晶体，即σ=σ3，而无其它应力分量。施加应力前，光率体方程为一旋转椭球体，其方程如下:

在单向应力作用下，光率体发生了变化，新光率体方程为［10-13］:

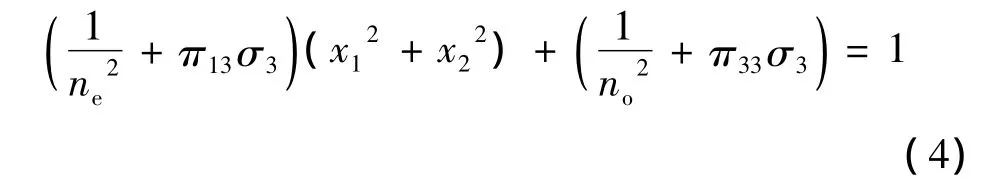
式中，ne为非常光折射率，n0为常光折射率，πij(i，j=1，2，…，6)为石英晶体的弹光系数，双折射率为:

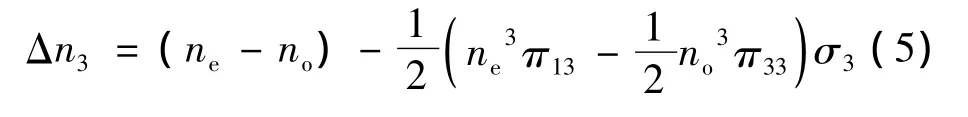
即除了原来的双折射率之外，附加了与应力σ3成正比的应力双折射。

(2)施加平行于Ox1轴的单向正应力σ=σ1，而无其它应力分量，新光率体方程为:

上式中出现了交叉项x2x3，表明新光率体的主轴已不是原来的Ox1，Ox2，Ox3轴了，需寻求新主轴方向，原有主轴Ox1未变，另外两个主轴Ox2，Ox3发生变化，将原来的平面Ox2-Ox3绕Ox1旋转θ角得到新坐标系，坐标转换如图2所示。

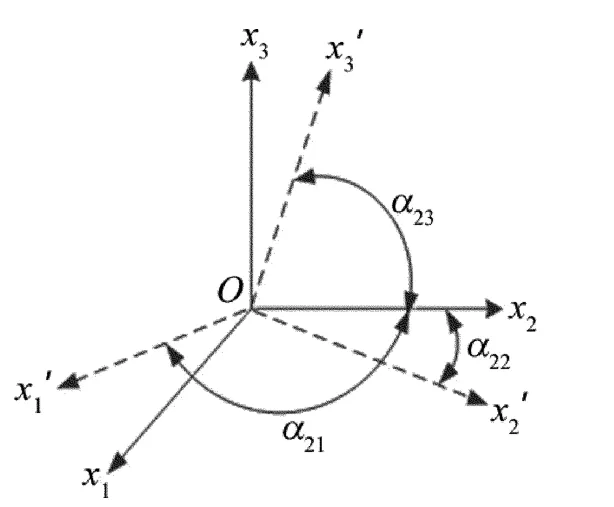
Fig.2 Figure of coordinate system transformation

图中，αij是新轴i与旧轴j基矢的方向余弦，θ角应由下式决定给出［10］:

光率体方程为:

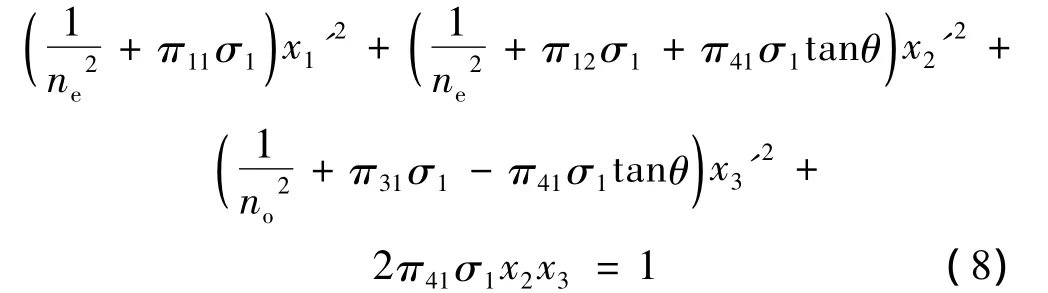
沿Ox2轴方向的双折射率变为:

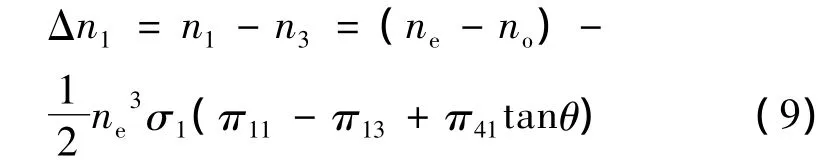
(3)同理，通过主轴变换可以推出施加平行于Ox2轴的单向机械应力σ=σ2，无其它应力分量，沿Ox2轴方向的双折射率为:

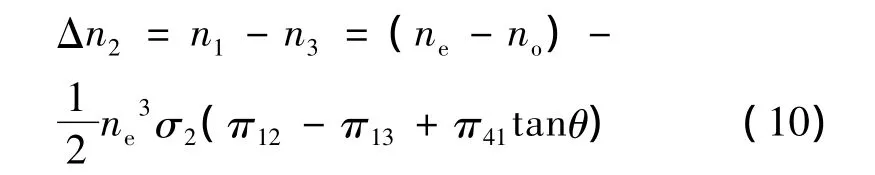
1.3 机械应力对石英滤波输出的影响

从Lyot型滤光片的基本原理出发，研究机械应力作用下Lyot型石英滤光片滤波输出的变化。

(1)施加在石英晶片的机械应力为平行于Ox1轴的单向正应力σ=σ1，由(2)式、(5)式得滤波片的透射比为:

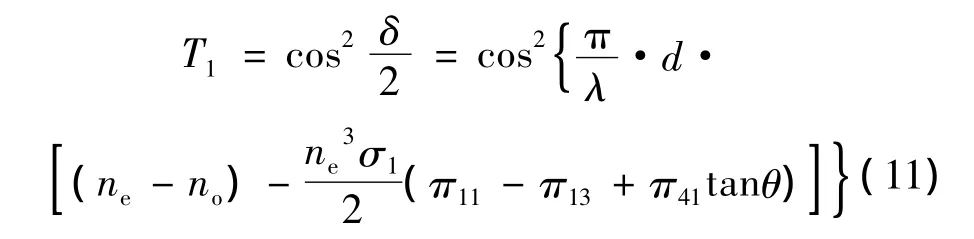
(2)施加在石英晶片的机械应力为平行于Ox2轴的单向正应力σ=σ2，由(2)式、(9)式得滤波片的透射比为:

(3)施加在石英晶片的机械应力为平行于Ox3轴的单向正应力σ=σ3，由(2)式(10)式得滤波片的透射比为:

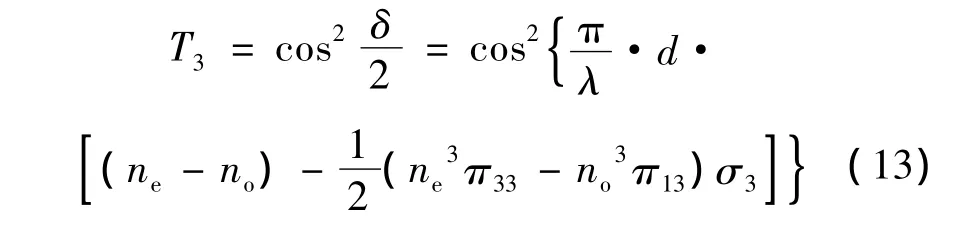
由(11)式、(12)式、(13)式可以看出，对一定波长的入射光λ，对应一定的δ值，若使δ取某一相应的值，T便可取最大值;对不同波长λ的入射光，使其透射比T值最大，机械应力σ改变，石英滤光片的输出改变。

以厚度d=7mm的石英晶体为例，图3是滤光片的理论透射曲线，波长范围为580nm～600nm，其中曲线1为无机械应力时滤光片的理论透射曲线;曲线2为应力平行于Ox1轴、大小为σ=0.0025N/m2时滤光片的理论透射曲线;曲线3为应力平行于Ox2轴、大小为σ=0.0025N/m2时滤光片的透射曲线;曲线4为应力平行于Ox3光轴、大小为σ=0.0025N/m2时滤光片的透射曲线。

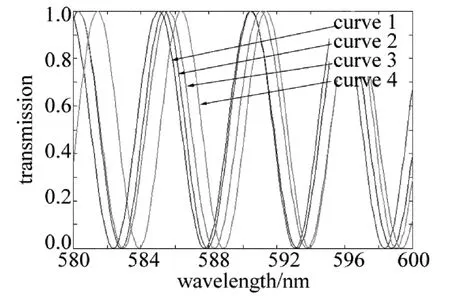
Fig.3 Transmittance curves without mechanical stress and with mechanical stress of 0.0025N/m2along the directions of Ox1，Ox2，Ox3axis

从图3中可以看出，当分别施加0.0025N/m2、平行于Ox1，Ox2，Ox3轴的机械应力在石英晶片上时，滤光片中心波长向长波长方向发生了漂移，漂移量分别为0.3nm，0.6nm，1.2nm。进一步通过数值模拟表明，当机械应力增大至0.005N/m2时，滤光片的中心波长向短波长方向漂移，说明机械应力大小不同，石英滤光片中心波长漂移方向不同。本文中重点研究不同方向机械应力对石英滤光片滤光输出的影响，实验和理论模拟机械应力大小均为0.0025N/m2，其它方向相同、大小不同的机械应力对石英滤光片滤光输出影响有待进一步研究和讨论。

2 实验设计与结果分析

为了检验以上理论的正确性，利用Ultra-6600系列紫外-可见分光光度计搭建了实验系统，对 Lyot石英双折射滤光片的透射光谱进行研究与分析。透射光谱测量系统框架如图4所示，测试系统由以下几个部分组成:光学系统、电源、数据采集与放大系统、主控板。光学系统主要由光源室、滤光片组、单色器、分光室和接收室组成。Ultra-6600系列提供5个滤光片，光谱范围为190nm～900nm。

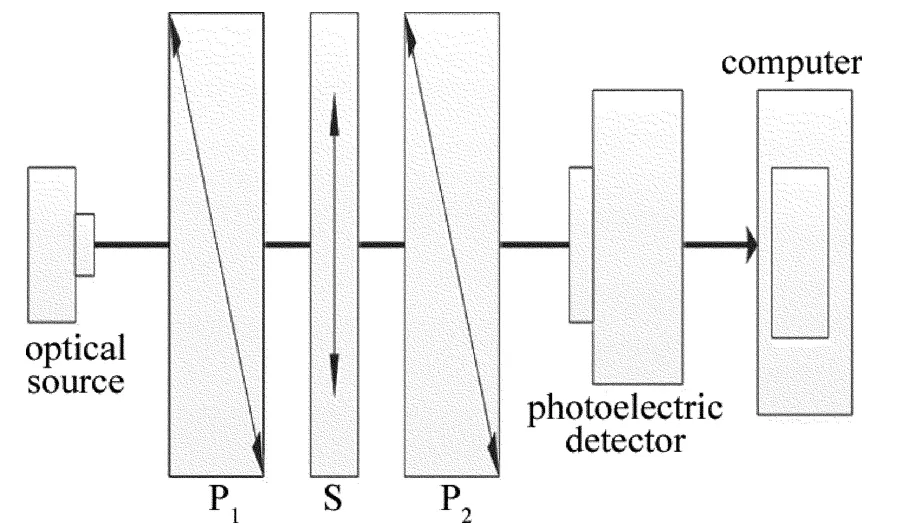
Fig.4 System frame

测试中使用的石英晶片厚度为7mm，实验中利用砝码和应力测试仪给石英晶片施加指定轴向的机械应力。测试得到的Lyot型石英双折射滤光片的透射曲线如图5所示。图5中光谱测量范围为580nm～600nm，光谱分辨率为0.1nm。其中曲线1为不施加机械应力时滤光片的透射曲线;曲线2为施加平行于轴Ox1、大小为σ1=0.0025N/m2的机械应力时滤光片的透射曲线;曲线3为施加平行于Ox2轴、大小为σ2=0.0025N/m2的机械应力时滤光片的透射曲线;曲线4为施加平行于光轴Ox3、大小为σ3=0.0025N/m2的机械应力时滤光片的透射曲线。

Fig.5 Transmittance curves of quartz filter without mechanical stress and with mechanical stress of 0.0025N/m2along the direction of Ox1，Ox2，Ox3axis

分析实验结果可知:(1)当石英晶片上分别施加平行于轴Ox1，Ox2，Ox3、大小均为 0.0025N/m2的机械应力时，滤波片中心波长向长波长方向漂移，漂移量分别约为0.4nm，0.6nm，1.0nm(理论值为0.3nm，0.6nm，1.2nm)，实验结果与理论模拟得到的结果是相当接近的，作者认为，存在的微小差别是由于石英晶片的厚度误差及机械应力测量误差所引起的，表明不同方向的机械应力对石英滤波输出的影响不同，且沿光轴Ox3方向的机械应力对石英滤波输出影响最大;(2)Lyot型滤光片透射率最高在92%左右，可认为是由于石英晶片的散射及偏振片吸收等原因导致的;(3)Lyot型滤光片透射率最低在6%左右，可认为是由于实验中所用偏振片的消光比不高及偏振片与石英晶体夹角不是严格45°等原因导致的。

3 结论

作者基于石英晶体的弹光效应，推导出不同方向机械应力作用下石英滤波输出与机械应力之间的关系，并进行数值模拟，且在580nm～600nm波段范围内进行了透射光谱测量。实验结果验证了上述理论的正确性，且表明在外加机械应力作用下，石英双折射滤波片中心波长发生偏移，中心波长漂移的方向与外加机械应力的大小有关，中心波长的漂移量与外加机械应力的方向有关，且沿光轴方向的机械应力对石英滤波输出影响最大。实验结果对制作封装、正确设计和使用石英双折射滤光片具有重要意义。

［1］ FRANCON M.Optical filter for radiations separation［M］.Beijing:Science Press，1984:37-42(in Chinese).

［2］ WANG X，YAO J.Transmitted and tuning characteristics of birefringent filters［J］.Applied Optics，1992，31(22):4505-4508.

［3］ HARRIS S E，AMMANN E O，CHANY I C.Optical network synthesis using birefringent crystals［J］.Journal of the Optical Society of A-merica，1964，54(10):1267-1279.

［4］ KONG Y，WANG Y M，ZHANG L P，et al.A quartz birefringent fiter insensitive to incident angle［J］.Opics and Laser Technology，2012，44(5):1497-1500.

［5］ KONG Y，YANG G W，HUANG X J.Multiple-stage liquid crystal tunedfilter［J］.Optik，2011，122(19):1723-1729.

［6］ OWENSJ C.Optical refractive index of air dependence on pressure［J］.Temperature and Composition，1967，6(1):51-58.

［7］ ZHANG J，LI G H.The theory of correcting the devation of retardation wave-plate［J］.Laser Technology，2005，29(6):639-640(in Chinese).

［8］ ZHANG Sh，WU F Q，WU W D.Characteristics of multistage quartz optical filter based on the optical rotatory dispersion effect［J］.Acta Physica Sinica，2008，57(8):5020-5026.

［9］ PENG D Y，SONG L K，LI K T，et al.Measurement of birefringence of liquid crystal with polarized light interference method［J］.Laser Technology，2014，38(3):422-424(in Chinese).

［10］ CHEN G，LIAO L J，HAO W.Crystal physics basis［M］.Beijing:Science Press，2007:332-337(in Chinese).

［11］ LIAO Y B.Polarized opticas［M］.Beijing:Science Press，2003:133-135(in Chinese).

［12］ LI J Zh.Handbook of optics［M］.Xi’an:Shanxi Science and Technology Press，1986:6-70(in Chinese).

［13］ ZHANG W Q.Optimized parameters of birefringent filter［J］.Acta Optica Sinica，2005，25(10):1420-1424(in Chinese).