几种小波在3维面形测量中的应用研究

蔡振华，陈文静，钟 敏

(四川大学电子信息学院，成都610064)

式中，W(a，b)为该信号的小波变换系数，φa，b=φ((x－b)/a)是母小波经过伸缩因子a和平移因子b得到的子小波序列，φa，b* 是 φa，b的复共轭。F(ω)为f(x)的傅里叶变换，ψ(aω)是小波函数 a－1φ(x/a)的傅里叶变换，ω表示空域x傅里叶变换后对应频域中

引 言

基于三角测量原理的结构光投影光学3维轮廓测量方法包含两大类:变换域分析方法和相移测量［1-4］方法。常用的变换域分析方法有傅里叶变换轮廓术［5］、窗口傅里叶变换轮廓术［6］、小波变换轮廓术［7-13］等。在这些测量方法中，变形条纹图通常是待分析物理量的信息载体，具有非平稳性特点。小波变换在处理非平稳信号方面具有先天优势，可以通过调整小波函数的尺度因子、旋转因子等参量，以不同的分辨率来分析信号，被称为信号分析的数学显微镜。小波变换被引入到结构光投影的光学3维测量领域，形成小波变换轮廓术。小波变换轮廓术采用“脊”［8-9］分析技术，利用调整尺度因子和旋转因子后获得一组小波变换系数，通过寻找每个位置小波变换系数的最大值来求出对应位置处条纹的相位信息，从而重建物体的3维面形。

小波变换轮廓术近年来得到深入研究，实小波和复小波均可以用来解调条纹相位。为了方便截断相位的展开，也研究了新的子小波定义［12］，使小波“脊”处的小波变换系数模值包含了条纹图的调制度信息，以指导相位的展开，减小相位展开过程中的误差传递。目前对小波变换轮廓术的研究主要从空域的相关运算展开，对各常用的小波的频谱分布特点对条纹处理带来的影响的讨论并未深入开展。作者从小波变换系数计算式的频谱表示形式出发，分析了几种局部特定好的小波函数的频谱特点，包含:1维Mexican hat和2维Mexican hat实小波，1维 Morlet和2维Morlet复小波以及由2维Morlet小波组合形成的Fan小波。通过比较以上几种小波函数的频谱分布，讨论条纹受到非线性和噪声影响时，分别采用以上小波函数用于小波变换轮廓术的相位计算精度的影响，也对比它们对具有不同形变特征的条纹图的相位解调精度。研究工作为基于小波变换轮廓术的应用提供了理论参考。

1 基本原理

1.1 光学3维面形测量基本原理

小波变换轮廓术的系统结构光路如图1所示。投影装置投射正弦结构光场到被测物体h(x，y)上，投影的光栅像受到物体表面高度的调制，成像装置从另一方向上采集的携带被测物体高度信息的变形条纹图表示为:

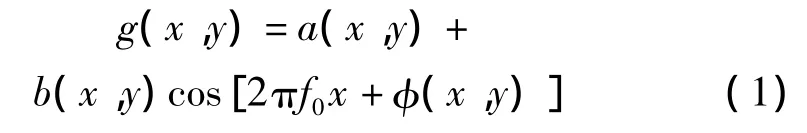
式中，f0为光栅频率，a(x，y)表示背景光强，b(x，y)是条纹对比度，φ(x，y)是变形条纹中携带的与被测物体有关的相位分布，设φ0(x，y)表示参考面(h(x，y)=0)对应的相位分布，Δφ(x，y)=φ(x，y)－ φ0(x，y)是物体高度分布对应的相位分布。根据测量系统的三角关系，Δφ(x，y)和物体高度分布h(x，y)之间的映射关系表示为:

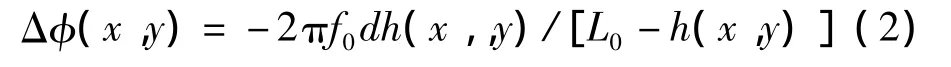
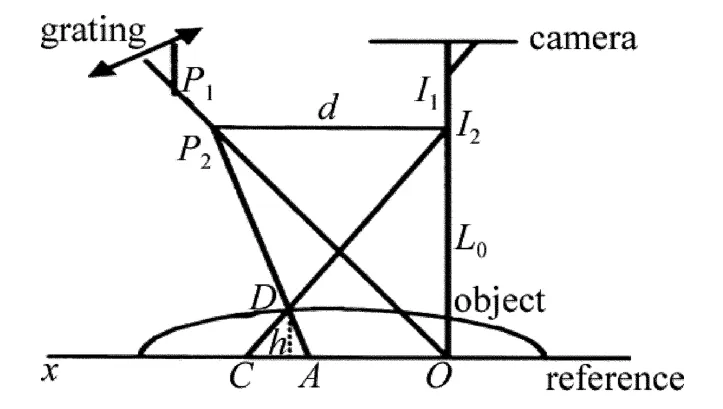
Fig.1 Optical geometry

1.2 小波变换轮廓术基本原理

1.2.1 1维小波变换定义 采用1维小波变换进行条纹相位计算，需要沿着光栅结构方向，逐一计算每行(列)的对应的正弦信号的小波变换系数，从中求解出相位信息。设条纹图g(x，y)沿着条纹结构方向的1维函数表示为f(x)，其1维小波变换可以表示为:的频率。可见小波变换既可以看作是空域信号与小波函数的相关运算，也可以看作在频域内坐标缩放小波函数的频谱对信号频谱进行滤波后的逆傅里叶变换，即对条纹图进行相位解调时，小波变换函数起着加权滤波器的作用。

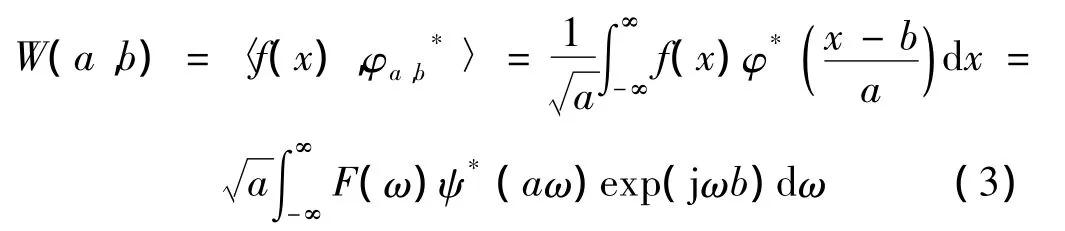
式中，W(a，b)为该信号的小波变换系数，φa，b=φ((x－b)/a)是母小波经过伸缩因子a和平移因子b得到的子小波序列，φa，b*是 φa，b的复共轭。F(ω)为f(x)的傅里叶变换，ψ(aω)是小波函数a－1φ(x/a)的傅里叶变换，ω表示空域x傅里叶变换后对应频域中

1.2.2 2维小波变换定义 条纹图g(x，y)的2维小波变换可以表示为W(a，bx，by，θ):

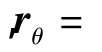
1.2.3 小波变换轮廓术相位获取 对于1维小波变换轮廓术，小波变换系数的模值A(a，b)和相位φ(a，b)可分别表示为:

式中，Re［］和Im［］分别表示取实部和虚部运算，找出b处小波系数的最大模值(称为“脊”)对应的尺度因子ar，从ar对应的小波变换系数中可以计算出变形条纹的截断相位 φ(ar，b)。同理，2-D小波变换系数W(a，bx，by，θ)的模值和相位分别表示为:

每个位置(bx，by)，“脊”处对应的最佳尺度记作ar，最佳旋转角为θr。从“脊”处可以计算出变形条纹的截断相位 φ(ar，bx，by，θr)。

小波变换处理过程遍历整幅变形条纹图后，可获得该条纹图中携带的截断在(－π，π］之间相位信息，扣除参考条纹中计算出的相位分布后，可得到物体高度对应的相位Δφ(x，y)，再经过相位展开可得到连续相位，从而重建被测物体的3维面形。

1维Morlet小波、1维Mexican hat小波、2维 Morlet小波、2维Fan小波、2维Mexican hat小波具有较好的局部特点，可以用于条纹分析中。下面先分析以上几种小波函数的频谱特点，再通过计算机模拟和试验研究条纹非线性和噪声以及条纹形变特征对采用以上小波函数的小波变换轮廓术的相位计算精度的影响。

2 常用母小波的时频特点

2.1 复 Morlet小波

1维复Morlet小波的空域和频域表达式分别为:

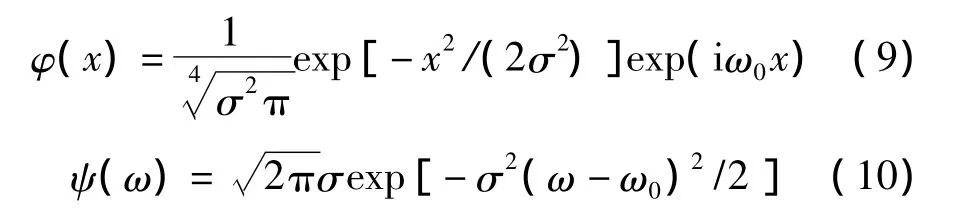
式中，ω0确定了函数的中心角频率。

2维复Morlet小波的时域和频域的表达式为:

2维复Fan小波的时域和频域的表达式为:

上面(9)式～(14)式中，x和y为空域变量，r和s为频域变量。σ确定了母小波的宽度(σ的值是母小波窗口宽度的大小)，为了满足容许条件，ω0常取2π左右值［13］。θ和θj控制2维小波的旋转方向，其中θj代表j个不同的角度，Nθ是叠加小波的个数。以上小波的时域和频域波形如图2、图3和图4所示。图2a和图2b是 σ=1，ω0=5.336rad/s时，1 维 Morlet小波空域和频域波形。

图 3a和图 3b 分别为 σ =1，θ=45°，ω0=5.336rad/s时，2维Morlet小波的空域分布的实部和虚部，图3c是该小波的频域分布，其频谱很窄。

Fig.2 1-D Morlet wavelet

Fig.3 2-D Morlet wavelet

Fig.4 Fan wavelet

图4是由4个不同方向2维Morlet小波组成的Fan小波的时域和频域图，其中 ω0=5.336rad/s，θj={0°，30°，60°，90°}。图 4a 表示该 Fan 小波的实部，图4b表示其虚部，图4c所示为σ=1时，Fan小波的频谱，通过调整Fan小波的宽度，可以构成一个形状复杂的频域滤波器。例如取σ=0.7时，Fan小波的频谱如图4d所示。

复小波的频谱分布作为一个宽度可调的加权滤波器，可用其选择出条纹在每个位置处的最佳局部基频分量来计算小波系数，从小波变换“脊”系数中可以得到准确相位分布。1维Morlet小波可在条纹载频方向提取出较为准确的频率信息;2维Morlet小波可实现在两个频率方向上的加权滤波处理，有更强的噪声抑制能力，但是该小波具有非常窄的频率结构，当变形条纹频谱中有效的基频分布较宽时，会因丢失太多的频率信息，导致相位的重建效果较差。Fan小波可以构成一个形状复杂的频域滤波器，用于基频分布较宽的条纹相位解调时，可以得到优于2维Morlet小波，但是Fan小波的空域分辨率较低。

2.2 实小波

1维Mexican hat小波的空域和频域表达式分别为:

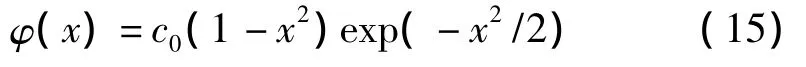
2维Mexican hat小波的空域和频域表达式分别为:

Fig.5 1-D Mexican hat wavelet

式中，x和y为空域变量，ωx，ωy为频域变量。1维Mexican hat小波的时域和频域分布如图5a和图5b所示。

2维Mexican hat小波时域和频域分布如图6所示。

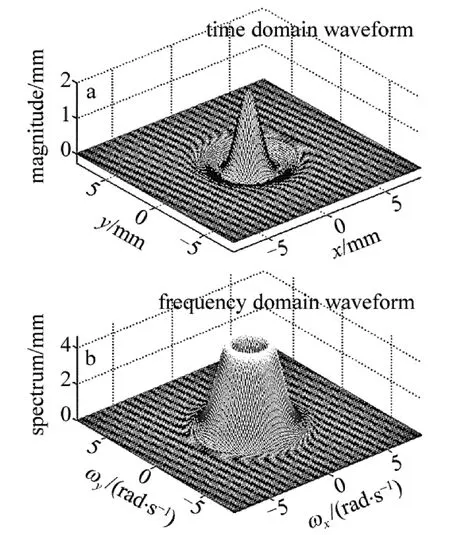
Fig.6 2-D Mexican hat wavelet

实小波的频谱有正负频率存在，不能直接用于条纹图解相位。可在小波变换前，先构造条纹信号的解析函数，再对其进行小波变换。以1维信号为例，解析信号的构成过程如下。

先计算信号的希尔伯特变换:

式中，g(t)为信号，t和τ均表示时间。则构成的解析信号表示为:

由于1/(πt)的傅里叶变换为－isgn(f)，则解析信号的频谱分布为:

式中，G(f)为g(t)的傅里叶变换。

即解析信号负频谱为0，正频谱是原来信号的正频谱的2倍，解析信号与原信号具有相同的相位信息。实Mexican hat小波的正负频域区，频谱的分布不是严格对称的，可以选择出更多的高频细节信息，其空域结构也具有较少振荡，用于小波变换轮廓术中，在物体边沿处，测量误差较小，但其对较大的噪声比较敏感。下面通过计算机模拟和实验来验证上述分析。

3 计算机模拟

采用结构光投影方式获取的条纹通常会受到投影和成像装置的非线性和系统噪声的影响。首先模拟条纹非线性和噪声存在时，基于1维Morlet小波、1维Mexican hat小波、2维Morlet小波、Fan小波以及2维Mexican hat小波的小波变换轮廓术的解相精度。由于不同小波具有不同的频谱特性，本文中也对比了以上所列小波解调具有不同特点的条纹图形变的精度。在随后的模拟过程中，正弦光栅空间周期为16pixel，背景a=0.5，对比度b=0.5，图像像素尺寸为256pixel×256pixel。

3.1 条纹的非线性对恢复结果的影响

Fig.7 a—the simulated object b—the deformed fringe pattern c—the sections of fringe patterns when γ =1 or γ =2 d—the reconstructed standard deviations processed by five wavelets

模拟物体由MATLAB提供的peaks函数表示，如图7a所示。受到其调制并取γ=2的变形条纹图表示为I(x，y)=g(x，y)γ，g(x，y)由(1)式表示，如图7b 所示。非线性的存在引起条纹偏离正弦分布，图7c中是γ值分别为1和2时，光栅栅线方向上的条纹局部剖面图对比。通常实际测量系统中商用投影仪和成像装置的组合非线性γ值在［1～3］之间。在此变换范围内，设步距为0.2，讨论不同γ取值带来的测量误差。采用不同小波函数的小波变换轮廓术的相位恢复标准差，如图7d所示。Mexican hat小波作为一个非对称的加权滤波器，可以较好抑制非线性引入的谐波分量对测量的影响，并有效保留物体的细节信息，所以重建结果的误差相对较小，2维Mexican hat小波的重建效果最好。Fan小波作为一个复杂的频带相对较宽的滤波器，非线性引入的谐波分量的存在使得其恢复结果误差相对较大。2维Morlet对非线性比较敏感，非线性引入的谐波分量增大，误差增大。此外，具有同一结构的2维小波重建的误差小于1维小波的重建误差。

3.2 噪声对恢复结果的影响

受到噪声影响的变形条纹可以表示为:gn(x，y)=g(x，y)+n(x，y)，n(x，y)为标准差可调的正态分布随机噪声，表示为N×randn(x，y)。设噪声标准差从0到0.25之间变化，间隔是0.01。图8a是含有较大噪声(标准差为0.25)的变形条纹图。图8b是1维Morlet小波、2维 Morlet小波、1维 Mexican hat小波、2维Mexican hat小波以及Fan小波恢复结果标准偏差图。图8c～图8g分别是1维 Morlet小波、2维 Morlet小波、Fan小波、1维Mexican hat小波和2维Mexican hat小波在噪声标准差为0.2时恢复结果。图8b可见，随噪声增大，2维小波对噪声的敏感度低于1维小波处理。同其它几个小波相比，1维Mexican hat小波的重建结果对噪声较为敏感，该小波的频谱具有非对称特点，更能较好获得对应物体细节的信息，重建误差相对较小。1维小波变换采用对条纹的每一行独立处理，重建结果在非载频方向上误差较大。

3.3 解调不同特征条纹图的相位精度比较

Fig.8 a—the deformed fringe pattern with noise(N=0.25)b—the standard deviations reconstructed by five wavelets in different noise rates c—the reconstructed phase by 1-D Morlet wavelet d—the reconstructed phase by 2-D Morlet wavelet e—the reconstructed phase by Fan wavelet f—the reconstructed phase by 1-D Mexican hat wavelet g—the reconstructed phase by 2-D Mexican hat wavelet

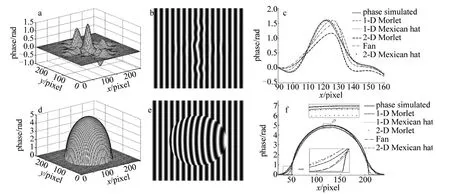
Fig.9 a—the simulated phase(sinc(x，y)(peaks)b—the deformed fringe pattern corresponding to Fig.9a c—the retrieved phase of the 120th row(from the 90th to 120th columns)by different wavelets d—the simulated phase(hemisphere)e—the deformed fringe pattern corresponding to Fig.9d f—the retrieved phase of the 128th row by different wavelet

(2)对面形简单但存在频谱分量丰富的边沿的物体，采用上述小波重建。以球缺作为模拟相位，如图9d所示。

图9e表示受其调制得到的变形条纹，图9f是不同小波重建的第128行的相位分布，实线是模拟的调制相位。采用Mexican hat小波能恢复出更多的细节信息。表1中给出了这几种小波恢复不同模拟相位结果的标准差。

Table 1 The reconstructed standard deviation errors of the different objects by different wavelets

4 实验

1组对比试验验证了5种小波函数对变形条纹相位解调能力。被测物体为“奥特曼”面具，CCD拍下参考条纹以及受物体高度调制的变形条纹，裁减像素尺寸为600×600的区域进行处理，裁减后的变形条纹如图10a所示。分别采用1维Morlet小波、2维Morlet小波、Fan小波、1维 Mexican hat小波、2维 Mexican hat对从中计算出对应物体高度的相位信息，得到的重建的相位分布如图10b～图10f所示。被测物体面形比较复杂，条纹对比度较低，对小波函数的空间分辨率的要求较高，1维Morlet小波恢复较好，2维Morlet小波频谱太窄，丢失了过多的细节信息，模型的嘴巴处形状被平滑了。Fan小波由于空间分辨率较低，虽然比2维Morlet在嘴巴处恢复的结果更好，但是在模型的头顶出现了错误，由图10d中得圆圈标记出。1维Mexican恢复出了细节但是存在震荡。2维Mexican hat恢复结果最好。

Fig.10 Experiment results

5 小结

通过对比1维Morlet小波、1维Mexican hat小波、2维Morlet小波、2维Mexican hat小波以及Fan小波的空域和频域特性，对它们在解调受到非线性和噪声影响的变形条纹的相位计算精度展开讨论，也对比它们处理具有不同形变特征的条纹图的相位解调精度。Maxican hat小波由于具有非对称的频谱特点，重建面形的细节保留较好，特别是在条纹噪声较小时，Maxican hat的重建精度比其它小波高，Fan小波的重建结果对噪声和非线性均不敏感，但是由于该小波的空域分辨率低，重建面形误差较大。由于物体面形变化引起的条纹频域频谱扩展，2维Morlet小波太窄的频带，会导致对条纹解相位时，太多细节信息的丢失，不太适合用于小波变换轮廓术中，除非条纹的变形量很小。计算机模拟和试验证明了作者的分析，研究结果对小波变换轮廓术的应用提供了理论参考。

［1］ SU X Y，LI J T.Information optical［M］.Beijing:Science Press，1999:288-299(in Chinese).

［2］ JIN G F，LI J Z.Laser metrology［M］.Beijing:Science Press，1998:337(in Chinese).

［3］ CHEN F，BEOWN G M，SONG M.Overview of three dimensional shape measurement using optical methods［J］.Society of Photo-Optical Instrumentation Engineers，2000，39(1):10-22.

［4］ SRINIVASAN V，LIU HC，HALIOUA M.Automated phase-measuring profilometry of 3-D diffuse objects［J］.Applied Optics，1984，23(18):3105-3108.

［5］ SU X Y，CHEN W J.Fourier transform profilometry:a review［J］.Optics and Lasers in Engineering，2001，35(5):263-284.

［6］ QIAN K M.Windowed fourier transform for fringe pattern analysis［J］.Applied Optics，2004，43(13):2695-2702.

［7］ LIONEL R W.Review of fringe pattern phase recovery using the 1-D and 2-D continuous wavelet transforms［J］.Optics and Lasers in Engineering，2012，50(8):1015-1-22.

［8］ ZHONG J G，WENG J W.Phase retrieval of optical fringe patterns from the ridge of a wavelet transform［J］.Optics Letters，2005，30(19):2560-2562.

［9］ LI S K，SU X Y，CHEN W J.Wavelet ridge techniques in optical fringe pattern analysis［J］.Journal of the Optical Society of America，2010，A 27(6):1245-1254.

［10］ LI S K，SU X Y，CHEN W J.Applications of two-dimensional wavelet transform on phase analysis of spatial carrier-fringe patterns［J］.Acta Optica Sinica，2010，30(6):1673-1679(in Chinese).

［11］ GAO Y，WANG A M，WANG F H，et al.Application of improved wavelet transform algorithm in image fusion［J］.Laser Technology，2013，37(5):690-695(in Chinese).

［12］ LI S K，SU X Y，CHEN W J.A new wavelet transform method for optical carrier-fringe pattern phase reconstruction［J］.Chinese Journal of Lasers，2010，37(12):3060-3064(in Chinese).

［13］ WANG Z Y，MA J，MINH V.Recent progress in two-dimensional continuous wavelet transform technique for fringe pattern analysis［J］.Optics and Lasers in Engineering，2012，50(8):1052-1058.