信号降噪中小波基与阈值的选取研究
2015-04-19姚运萍
□ 罗 淼 □ 姚运萍
兰州理工大学机电工程学院 兰州 730050
在信号的生成与传输过程中,经常由于受到噪声的影响使得质量变差,因此有针对性地从测量数据中获得有效信息,对信号进行降噪是许多分析过程的重要一步[1]。传统的降噪是将被噪声干扰的信号通过滤波器将无用噪声成分去除,但对脉冲信号、白噪声、非平稳过程信号等,具有一定的局限性。近些年来,由于小波理论的不断发展,使其在信号降噪方面有独特的优越性,因而被广泛应用。小波分析的一般过程是先把信号分解为小波系数,然后对分解出来的系数根据问题的要求做一些处理,再用小波重建方法恢复信号[2]。
1 小波降噪方法
1981年,法国地理物理学家Morlet在分析地质探测数据时,基于群论首先提出了小波分析这一概念,随后他和法国物理学家Grossmann开始一起共同研究小波理论,发展了连续小波变换的理论体系。1985年,法国数学家Meyer、物理学家Grossmann及比利时数学家Daubechies等共同研究,得到了一组离散小波基。1988年,Daubechies提出了具有紧支集的正交基,即Daubechies基。美国研究者Weaver等最早将小波变换用于图像降噪[3],Weaver等所用的算法是一种简单的阈值降噪法。所谓阈值滤波就是把小波系数的幅值同一个阈值进行比较,若小波系数的幅值比这个阈值小,则把小波系数置为0;若小波系数的幅值比这个阈值大,则把小波系数保留或进行修改后保留。随后美国数学家Donoho等对小波阈值滤波算法作了系统阐述,成为小波滤波方法的一个具有里程碑意义的研究成果。
1.1 小波变换原理
小波函数是由一个小波“母函数”经过伸缩和平移而得到的一簇函数。若φ(t)为小波母函数,则由其派生出来的小波函数为:
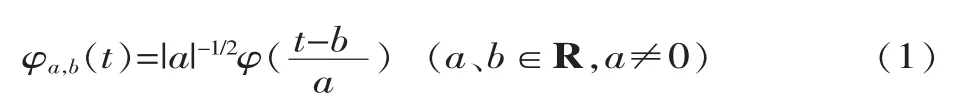
式中:a是伸缩的尺度;b是平移的距离。
并非任何函数都可以成为小波母函数,小波母函数必须满足一定的条件。令:

则 φ(t)为小波母函数的必要条件为 Cφ<+∞,Cφ<+∞又叫作可容许(admissible)条件。可容许条件说明ω=0 时,一定为 0,即:

这说明函数φ(t)必须要有一定的波动性。函数f(t)的连续小波变换可表示为:


可以看出,小波变换是一种可以保持信息内容的可逆变换,信息保存于小波变换系数中,经过反变换后即可恢复。
在实际应用中,需要将小波离散化才有意义[4]。离散小波就是将连续小波的尺度参数和平移参数离散化,若令 a>1,b>0,则定义离散小波为:

小波变换是对Fourier变换的继承和发展,使变换结果既有一定的频率分辨率,又有一定的时间分辨率。小波变换的一个重要特性是其具有“变焦”的特性,对非平稳信号具有很强的适应性,因此很适合对信号进行降噪处理。
1.2 降噪基本原理
假设信号 f(n)被噪声污染后为 s(n),则可以建立噪声模型:

式中:e(n)为噪声;σ 为噪声强度。
在简单情况下可假设e(n)为高斯白噪声,且σ=1。利用小波变换去噪就是要通过抑制噪声e(n),从而尽可能恢复原信号 f(n)。
从统计学的观点看,这个模型是一个随时间推移的回归模型,也可以看作是在正交基上对函数f(n)的无参估计[5]。
小波去噪的整个过程可以分以下三步进行。
第一步,利用离散小波变换(DWT)进行信号分解,选择适当的小波基以及分解层数。
第二步,确定小波域的阈值,对小波系数进行阈值截断。
第三步,利用截断后的系数进行小波重构。
1.3 阈值的处理
小波阈值是根据噪声模型和原信号的信噪比来确定的,在模型中,这个量由标准方差σn来表示。在得到夹杂白噪声的信号后,可以由噪声强度σ来确定阈值。最常用的确定方法为Donoho提出的统一阈值,阈值Thr的选择满足:

式中:N为信号的长度。
这种方法在实际应用中效果不是很好,比较常用的阈值选取方法有以下几种[6]。
(1)基于无偏似然估计的软阈值估计(Rigrsure),最佳阈值通过选择风险最小的阈值达到。
(2) 长度对数阈值 (Sqtwolog), 其阈值等于
(3)启发式阈值(Heursure),这种方法是长度对数阈值和软阈值估计的综合,利用启发函数在上述两种阈值估计方法中选取一个。
(4)最小极大方差阈值(Minimaxi),这种方法利用求得的回归函数与原信号的方差在最坏的情况时的最小值得到阈值,使选取的阈值产生最小均方误差的极值。
笔者所用的阈值选择方法先是利用Birge-Massart算法求得小波变换阈值,再根据合适的阈值确定阈值选取范围,最终取得最优阈值。Birge-Massart是针对给定的分解层数j,保留j+1以及更高层的系数,然后对第 i层(1≤i≤j),保留绝对值最大的 ni个系数:

式中:M和α是经验系数,在缺省情况下为第一层分解后的系数长度,在降噪时α=3。
选择阈值函数对小波系数进行阈值处理,即对其系数进行截断。常用的阈值函数主要有硬阈值函数和软阈值函数[7],如图1、图2所示,图中横坐标表示信号的原始小波系数,纵坐标表示阈值化后的小波系数,T为估计阈值。
硬阈值函数:

软阈值函数:

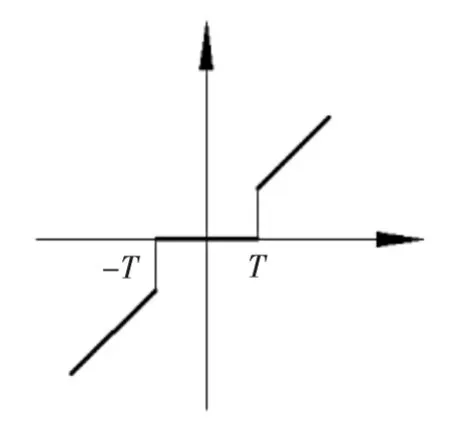
▲图1 硬阈值函数

▲图2 软阈值函数
硬阈值方法可以较好地保留信号边缘等局部特征,但滤波后信号容易突变,产生较大的振荡(称为吉布斯现象)[3];软阈值处理后信号较为平滑,但易造成模糊等失真现象。
2 小波降噪的MATLAB仿真
测试信号采用Doppler信号。小波基的一般选取原则有正交性、紧支性、对称性、平滑性、消失矩阵阶数,由于一般小波基的选择是根据与原信号相似原理,所分析的信号和所选小波基需存在一定的相似性。sym小波的构造类似于db小波族,两者的差别在于sym小波有更好的对称性[8]。故对Doppler信号进行降噪处理,采用 symN小波基。 初选 symN(N=1,2,…,15)为预选小波基系列,给Doppler信号加入高斯白噪声SNR为16 dB。
对于降噪效果的评估,采用最小化平均平方误差MSE(Mean Squared Error)及信噪比 SNR(Signal to Noise Ratio)来进行评价:

式中:xi为原图像第i个像素;为降噪后图像的第i个像素。

对加有噪声的Doppler信号按照硬阈值函数,分解层数初选为四层进行降噪处理。信号的信噪比越高,最小化平均平方误差越小,则表明降噪效果越好。
各小波基对信号降噪后的效果见表1,从表中可以看出,不同的小波基降噪效果不同,对于测试信号而言,sym10、sym13、sym15降噪效果较好。 对于不同的信号,小波基的选取决定降噪的好坏。经过多次仿真发现,sym10小波基对于Doppler信号的降噪效果较好,最终选取sym10小波基作为降噪过程采用的小波基。使用Birge-Massart算法获取小波变换的最佳阈值在0.57左右,为确定最优阈值,可将阈值搜索区间定为0.55至0.65,各阈值去噪效果对比如图3所示。最终经过多次仿真,确定最优阈值为0.6。确定小波基和阈值后,进一步确定最优分解层数。实验取分解层数为1~10层,不同分解层数的降噪效果见表2。
从表2的实验结果中可以看出,分解层数小于4时,降噪后的信号有明显的突变、尖峰情况。分解层数为3时的降噪效果如图4所示。当层数逐渐增加,效果逐渐平滑。分解层数为5、6、7层时,降噪效果较好,信号比较平滑,最后经过综合评定,选定最终的分解层数为6层。降噪后的信号如图5所示,采用上文提出的4种阈值选取规则对原信号进行降噪处理,各种方法得到降噪效果见表3。
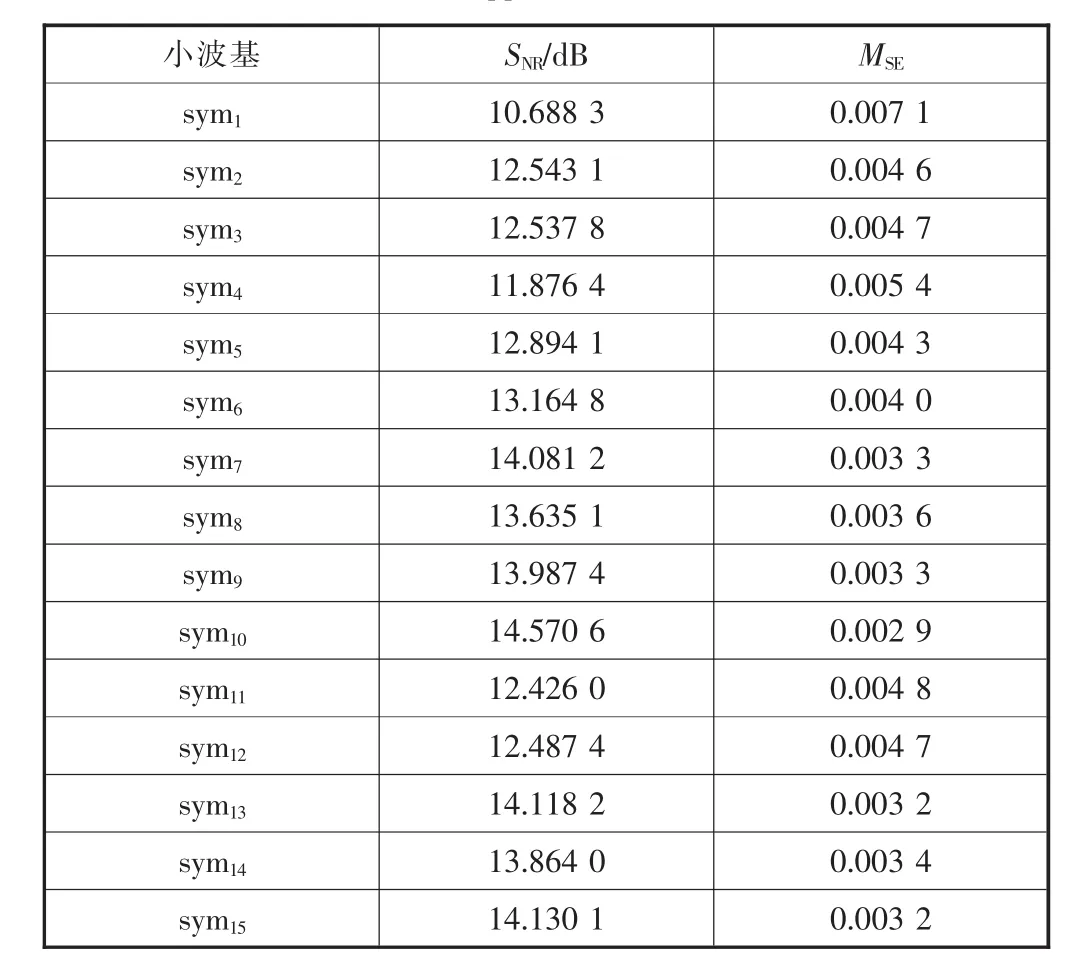
表1 各小波基对Doppler信号降噪后的效果评价
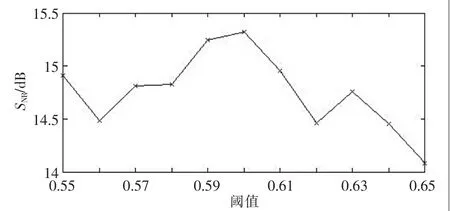
▲图3 不同阈值的去噪效果曲线图
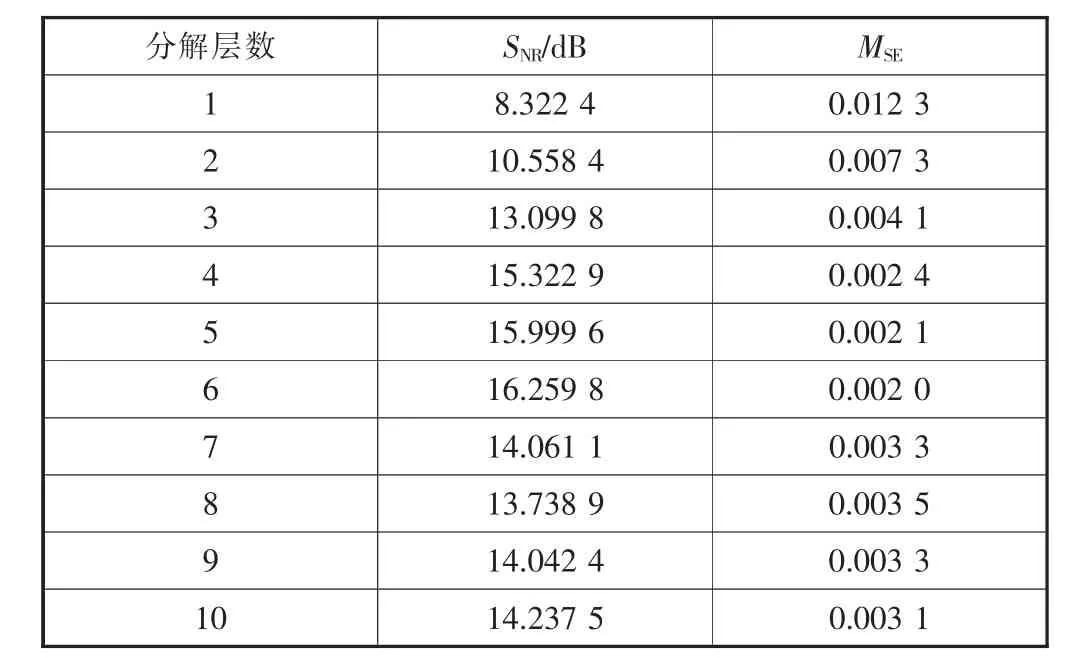
表2 不同分解层数的降噪效果

表3 不同阈值选取规则的降噪效果
从表3中可以看出,笔者所采用的小波基及阈值选取方法的降噪效果优于其它方法。
3 结论
通过分析可知,根据相似性原理,对Doppler信号的降噪处理采用sym小波基,其中小波的分解层数对信号的去噪影响较为显著,分解层数较小时,经过降噪处理的信号有突变和尖峰现象,随着分解层数的增加,信号逐渐趋于平滑,得到较好的降噪效果。
对于小波基的选择是一项艰难而又复杂的工作,笔者仅通过对Doppler信号降噪过程的小波基与阈值选取做了有限的分析,对于实际复杂信号降噪中的小波基与阈值选取需根据不同情况进行。
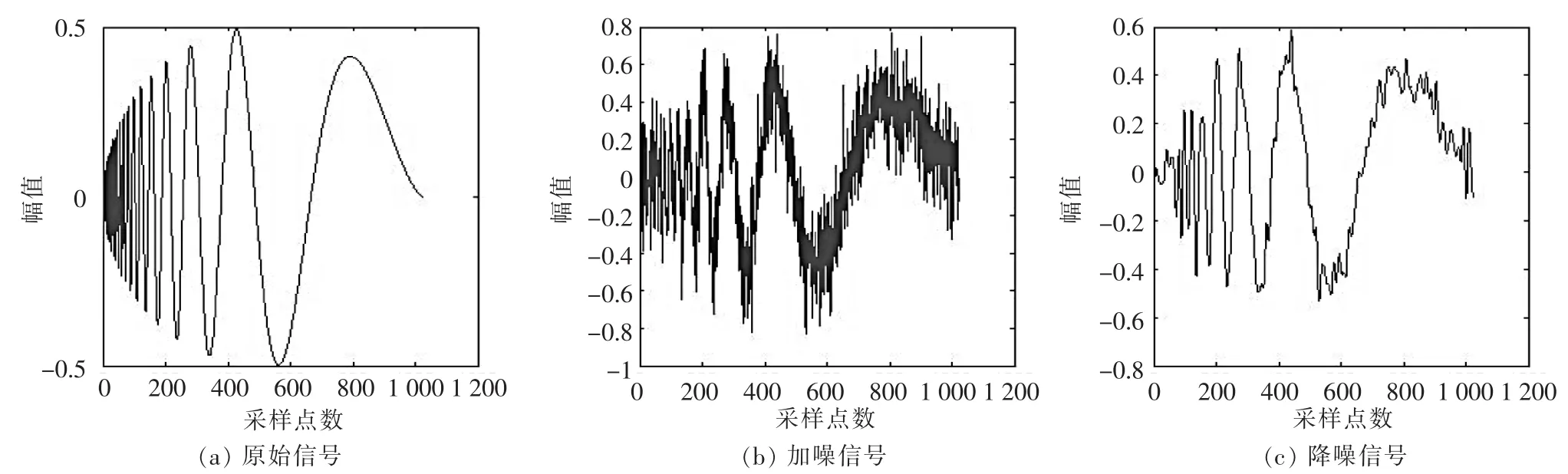
▲图4 分解层数为3时的降噪效果
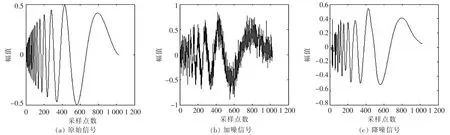
▲图5 分解层数为6时的降噪效果
[1]倪林.小波变换与图像处理[M].合肥:中国科学技术大学出版社,2010.
[2]李保霖,赵建川,蔺文彬.小波分析在信号降噪中的应用[J].电子设计工程,2013,21(9):39-42.
[3]姜三平.基于小波变换的图像降噪[M].北京:国防工业出版社,2009.
[4]高成,董长虹,郭磊,等.Matlab图像处理与应用[M].北京:国防工业出版社,2007.
[5]吴伟,蔡培升.基于MATLAB的小波去噪仿真[J].信息与电子工程,2008,6(3):220-222,229.
[6]许文博,武晓春,邢建平.一种新的小波阈值去噪方法[J].兰州交通大学学报,2012,31(3):120-124.
[7]周伟.基于MATLAB的小波分析应用[M].西安:西安电子科技大学出版社,2010.
[8]董长虹,高志,余啸海.Matlab小波分析工具箱原理与应用[M].北京:国防工业出版社,2004.
