基于AHP-FCE模型的产品再制造风险评价*
2015-04-19张小艳刘文慧
□ 张小艳 □ 刘文慧
西安工程大学机电工程学院 西安 710048
目前,我国再制造产业发展仍处于研究探索阶段,存在法律体系不健全、市场监管缺失、相关技术和设备落后等情况,严重阻碍了再制造产业的发展[1];忽略风险管理造成再制造活动失败的案例屡见不鲜。由此可见,为了确保废旧资源中蕴含的价值最大限度效益化,对再制造活动进行风险管理是必不可少的。
对产品再制造进行风险管理,首要任务是确定影响再制造的关键风险因素。在文献[2-7]中,主要从废旧品的回收、拆解、清洗、加工等不同阶段定性地分析了影响再制造的风险因素。在文献[8-10]中,从不同风险识别的角度探讨了影响再制造的风险因素,并对风险进行定量化评价。为了有效应对产品再制造的风险,研究设计一套产品再制造风险评价指标体系及评价标准,对再制造可持续发展有着非常重要的意义。笔者在系统识别再制造风险因素的基础上,构建了包括市场风险、设备风险、技术风险、管理风险、成本风险和政策风险的评价指标体系,并对风险进行定量评价,得出风险状态,为企业提升风险管理能力、降低风险水平提供一种新的理论基础和方法论。
1 产品再制造风险识别
再制造在带来巨大效益的同时,也伴随着潜在的风险,因此,及早分析再制造过程中各种类型的风险,并进行预警管控,防患于未然是十分必要的。产品再制造风险分为市场风险、设备风险、技术风险、管理风险、成本风险和政策风险。
(1)市场风险。这类风险主要存在于废旧品回收和再制造产品导入市场两个阶段,目前,再制造市场监管力度不严,导致市场混乱,消费者对再制造产品的认知度低。此外,产品销售渠道、营销能力等不确定因素,均可能影响产品再制造活动的成败。
(2)设备风险。再制造产品经过回收、拆解、清洗、检测、加工、装配等环节后投入市场,而设备选择或操作的不当,可能会导致拆解效率低下、零件利用率低、清洗效果差以及生产效率低等一系列风险。
(3)技术风险。我国再制造产业仍处于研究探索阶段,存在相关技术配套程度低、关键技术研发周期长或通用性低等缺陷,对废旧件利用率、劳动生产率、产品质量、再制造成本、可再制造性影响显著,甚至会导致再制造活动停滞不前,中途而废。
(4)管理风险。再制造过程中管理不力,可能会导致原材料供应不足、废旧件回收计划或生产计划制定困难等诸多阻碍,传统的制造管理体系已不能适应再制造生产模式,加大了企业管理难度,因此须避免管理不力造成再制造效益的损失。
(5)成本风险。这类风险贯穿于再制造的整个生命周期,易影响产品的市场竞争能力和企业盈利能力,回收利用率、废旧品拆卸难度、回收渠道、投资规模、对外界环境的损害及相关处罚等不确定因素均会影响产品再制造的成本。
(6)政策风险。这类风险主要通过法律缺失和过度限制来影响再制造活动。比如:再制造行业缺乏严格的市场准入制度,导致再制造市场混乱,虽已有支持再制造产业发展的纲领性文件,但缺少明确的实施措施,可操作性小,因此政策因素所带来的风险也是不容忽视的。
综上所述,可构建的风险评价指标体系见表1。
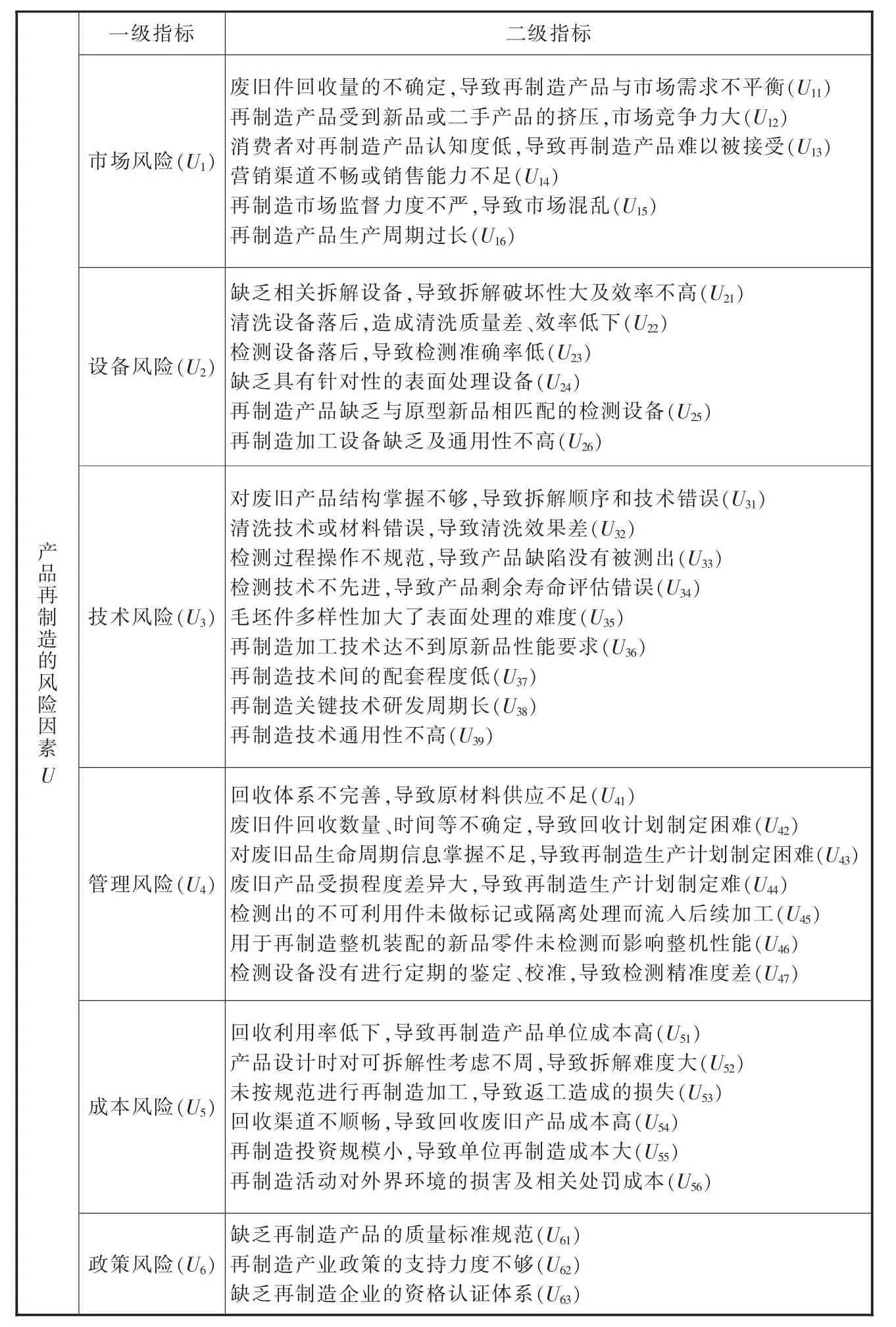
表1 产品再制造风险评价指标体系
2产品再制造风险评价模型构建
2.1 确定评价指标体系
在明确影响产品再制造的风险因素的前提下,根据各指标因素之间的关联程度及上下层隶属关系,构造完整的产品再制造多层次评价指标体系。笔者采用1-9标度法[11]构建指标体系并进行量化。
2.2 应用层次分析法(AHP)确定各指标权重
利用AHP确定各层次指标的权重,首先建立各层指标判断矩阵A,然后采用方根法来计算判断矩阵的一致性,其步骤如下。
(1)计算判断矩阵A每一行元素的乘积:
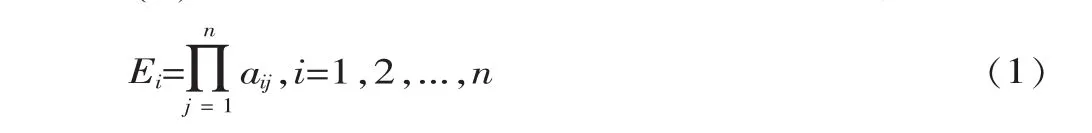
(2)计算 Ei的 n次方根
(5)进行一致性检验,判断矩阵的一致性指标为:CI=(λmax-n)/(n-1),它与平均随机一致性指标 RI之比为随机一致性比率,记为CR。当CR=(CI/RI)<0.1时,一致性检验通过。
2.3 应用模糊综合评价法进行综合评价
模糊综合评价法是利用模糊集数学法进行评价的一种方法,采用隶属度理论将评价目标定量化[12],其基本步骤如下。
(1) 确定评语集 V,V=(大,较大,一般,较小,小)=(V1,V2,V3,V4,V5),并赋予评语集 V 以不同分值,采用百分制 Z=(90,80,70,60,40)。
(2) 确定评判矩阵 R,R=Ri(i=1,2,...,6),通过合成算子 Q=W*Ri(* 为模糊合成运算符)合成相应的各因素 评价矩阵,归一化后建立总评价矩阵Q0=[Q1,Q2,Q3,Q4,Q5,Q6]T。
(3)产品再制造风险评价矩阵Si=W*Qi,然后确定产品再制造风险评价总得分,即 Fi=Si×ZT,其中,F 为风险评价得分,ZT为评语集的赋值。将总得分与评价等级表2进行比照,得到产品再制造的风险状况。

表2 风险评价等级表
3 产品再制造风险评价
3.1 建立产品再制造风险评价指标体系
基于上述产品再制造风险评价指标体系,产品再制造风险指标体系包括6个一级指标和37个二级指标。
3.2 确定各指标权重
3.2.1 构造风险评价的三层次递阶结构
根据产品再制造风险评价所涉及的方面,确定了评价的三层因素(见表1),即目标层 U、指标层 Ui=(U1,U2,…,U6)、二级指标层 Uij=(U11,U12,...,U63)。
3.2.2 确定各层指标的权重
组织专家评估组进行调查问卷,确定评价指标间的相对重要程度,依照2.2中层次分析法的计算步骤及公式,利用MATLAB软件计算,并对其进行一致性检验,见表3。
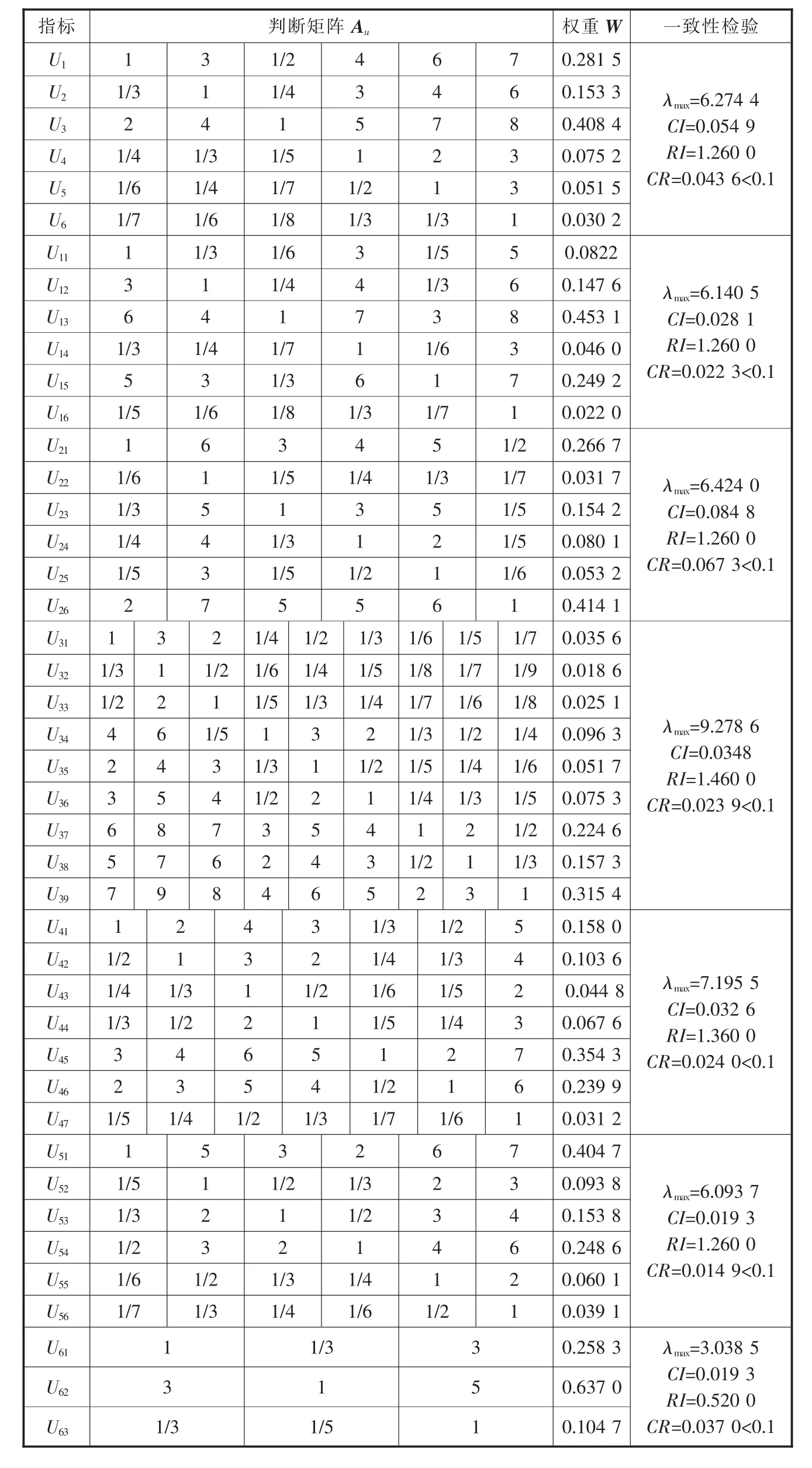
表3 判断矩阵及一致性检验
3.3 建立评价矩阵及风险评价
请20名专家根据产品再制造风险评判标准对37个二级指标进行模糊综合评判,经统一整理和归一化处理,汇总得出评判矩阵如下。


3.3.1 单项风险评价
单项风险评价即对一级指标进行评价。依据2.3,根据权重及模糊评价矩阵,分别对市场风险、设备风险、技术风险、管理风险、成本风险和政策风险进行风险等级评价。
市场风险对产品再制造风险评价的评价矩阵为Q1=W1*R1=(0.205,0.197 8,0.247 9,0.254 7,0.124 0),参照评语集的不同赋值,可得出市场风险评价的得分Fu1=Q1×ZT=0.205 0×90+0.197 8×80+0.247 9×70+0.254 7×60+0.124 0×40=71.869 0。 根据风险等级表 2,得出市场风险属“较强”等级。考虑到篇幅限制,其余指标风险等级评价不一一列出,综上得出一级风险指标的风险等级,见表4。

表4 一级指标风险等级
3.3.2 综合风险评价
将判断矩阵归一化,建立总评价矩阵Q=[Q1,Q2,Q3,Q4,Q5,Q6]T,即:
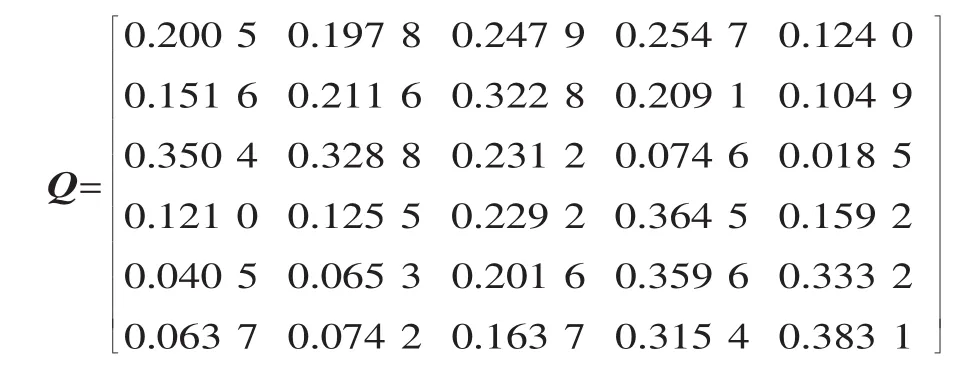
产品再制造风险评价矩阵 S=W*Q=(0.235 9、0.237 4、0.246 3、0.189 7、0.099 2)。 参照评语集的不同赋值,可得产品再制造风险评价的总得分F=S×ZT=0.235 9×90+0.237 4×80+0.246 3×70+0.189 7×60+0.099 2×40=72.814 0。将总得分对照风险评价等级表 (见表2),得出产品再制造的风险等级属较强。
4 结论
通过对产品再制造风险评价结果可以看出,产品再制造的风险等级属较强,说明企业在开展再制造业务时,必须提高风险管理能力,降低风险带来的损失。
笔者在利用层次分析法确定权重时带有一定的主观性,并假设同一层次指标是彼此独立的,没有考虑到指标因素之间的相互影响关系,这在一定程度上影响了评价结果的准确性,后续需要进一步对此项工作深入研究。
[1]高领.我国再制造产业发展的“三大阻力”[J].中国国情国力,2012(10):53-54.
[2]刘驿闻,张勇,姚英.我国废旧汽车回收利用现状及对策研究[J].价值工程,2012(19):308-309.
[3]刘晓培.报废汽车回收影响因素分析及其系统设计[D].重庆:重庆大学,2008.
[4]田广东.产品拆解概率评估方法及规划模型研究 [D].长春:吉林大学,2012.
[5]迟琳娜.再制造影响因素研究现状评析[J].胜利油田党校学报,2010,23(6):44-48.
[6]Thierry M C, Salomon M, Van Nunen, et al.Strategic Production and OperationsManagement Issues in Product Recovery Management [J].California Management Review,1995,37(2):114-135.
[7]谢家平,赵忠,孔令丞,等.再制造生产计划的影响因素及其模式[J].系统工程,2007,25(7):53-59.
[8]李聪波,刘飞,谭显春,等.基于风险矩阵和模糊集的绿色制造实施风险评估方法 [J].计算机集成制造系统,2010,16(1):209-214.
[9]王秋莲.基于神经网络的再制造系统风险评价[J].科技广场,2010(8):215-217.
[10]刘渤海.再制造产业发展过程中的若干营运管理问题研究[D].合肥:合肥工业大学,2012.
[11]王汉斌,杨鑫.一种基于AHP-RS的组合权重确定方法[J].中国安全生产科学技术,2010,6(6):155-160.
[12]汪应洛.系统工程[M].北京:机械工业出版社,2009.
