电镍导电棒矫直机结构参数及矫直压下量的设计

2015-04-19孙东明

机械制造 2015年12期

□ 童切 □ 孙东明 □ 姚辉 □ 金岩

1.昆明理工大学机电工程学院昆明 650500 2.金川集团股份有限公司镍冶炼厂甘肃金昌 737100

国内某镍冶炼厂，将尺寸为φ36 mm×3 mm×1 350 mm的紫铜圆管作为导电棒使用，与方管相比增加了导电棒与吊耳的接触面积，管状设计减少了导电棒上铜的消耗。但是，在粗镍电解精炼过程中，阴极板导电棒易受外力作用发生弯曲变形，这容易使阴极板与阳极板在隔膜电解槽内发生短路，同时会导致电解槽内单位面积排板数量的下降，直接影响电镍的质量和生产效率。其次，弯曲变形会影响其在抛光机和穿棒机中顺利通过[1]。所以，在生产过程中应及时对弯曲导电棒进行矫直。

针对紫铜圆管的结构、尺寸等特点，决定采用一组U形矫直辊进行矫直，形状如图1所示。辊距P、辊径D′、辊数n、辊速v、辊长L为矫直机的基本参数，对矫直质量、设备能耗和尺寸等均有影响。

1 矫直曲率比方程式

紫铜的应力应变模型如图2所示。假设圆形棒材的断面尺寸为φD，D=2R，根据图2得其弯矩为：

式中：σ1=zσt/Rt=zσt/（Rζ）；σ2为强化后的应力；Rt为弹性核心半径；σt为弹性极限；为圆形断面任意高度z处的断面宽度；弹区比ζ=Rt/R。

设σd、εd为表层的最大应力与应变，金属的强化弹性模数为E′，强化因子为λ，则：

将式（2）代入式（3）得：

再将式（4）代入式（1）得：

圆棒的弹性极限弯矩为Mt=πR3σt/4，故：

▲图1 U形矫直辊

▲图2 弯曲应力应变图

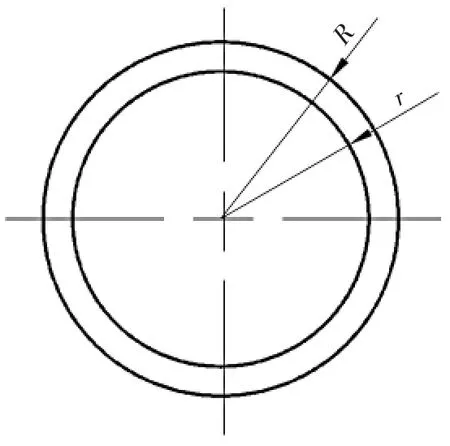
▲图3 紫铜圆管尺寸

导电棒的尺寸如图3所示，假设粗棒半径为R，细棒半径为r，粗棒弹区比ζ1=Rt/R；细棒弹区比ζ2=Rt/r；粗棒弹性极限弯矩 Mt1=πR3σt/4，细棒弹性极限弯矩Mt2=πr3σt/4=a3Mt1，a=r/R=ζ1/ζ2。

依据式（6）得粗

棒弯矩为：

管材的弯矩实质上是通过粗细两个棒材的弯矩之差来求得的[2]，式（7）、式（8）两式相减得圆管弯矩为：

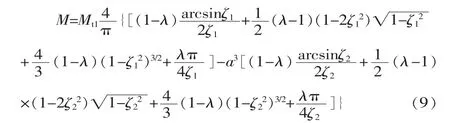
将管材的弹性极限弯矩 Mt′=πR3（1-a2）σt/4=Mt1（1-a4）、λ=0.11、a=30/36 代入式（9），可得：

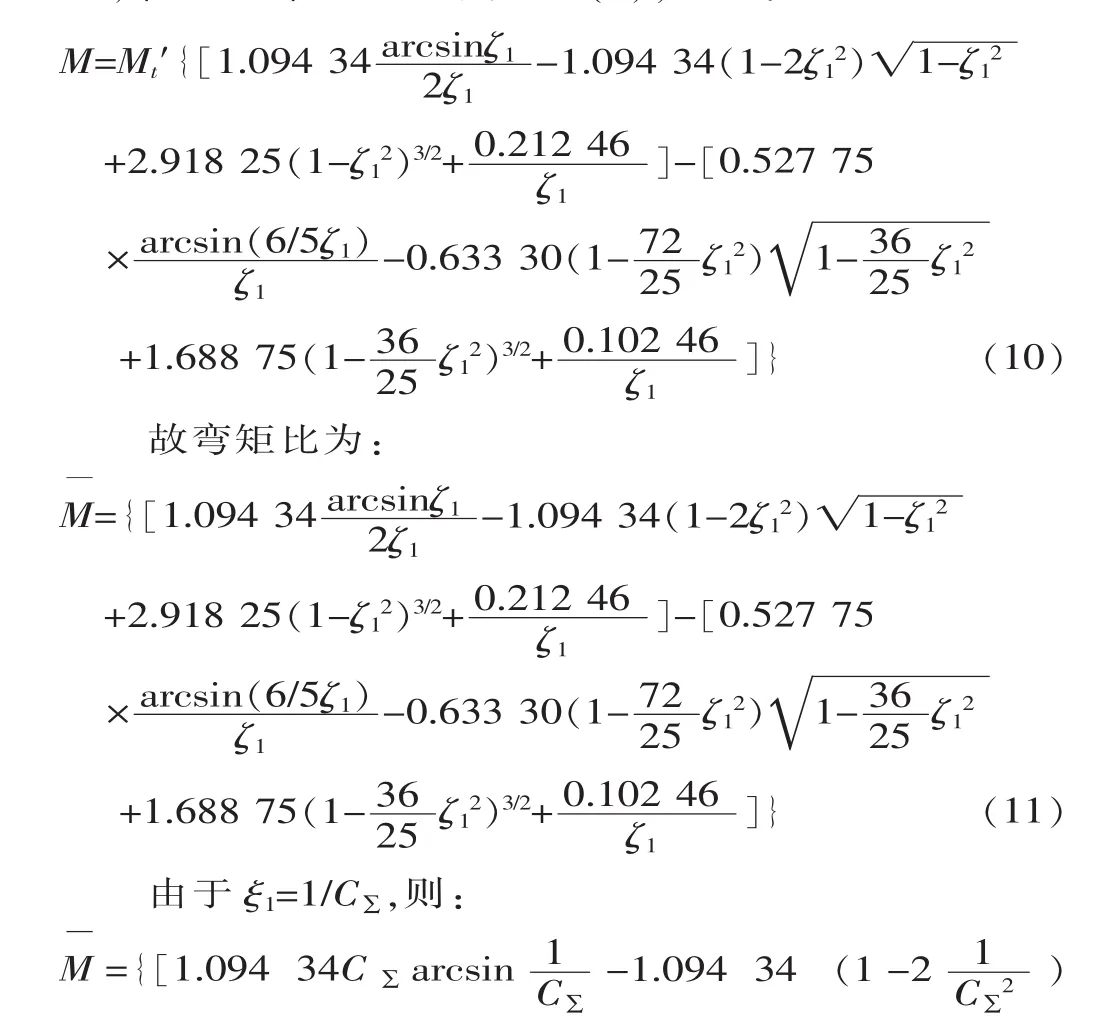
式中：CC为残留曲率比；Cw为压弯曲率比；Cf为弹复曲率比；C0为原始曲率比；C∑为总曲率比。

2 可调辊压下量

平直度和曲率比满足以下关系[3]：

式中：Δ为导电棒平直度，mm/m；C为弯曲曲率比；H为紫铜圆管的高度，mm；E为弹性模量，Pa；l为导电棒长度，mm。

紫铜圆管参数：屈服强度 σt=100 MPa，E=125 GPa，H=36 mm，l=1.35 m。导电棒原始平直度为Δ=15 mm/m，要求其在矫直后的平直度小于Δ=1 mm/m。因此，原始曲率比C0=±1.481，矫直后允许的残留曲率比CC=±0.099。

考虑到矫直对象为紫铜圆管，决定采用大变形-小变形混合矫直方案，第二、三辊处采用大变形。为防止管材塑性压扁，将 ξ1=a-1=0.733 3代入式（11），得Mmax=1.231 5，压弯曲率比Cw2=Cw3=2Mmax=2×1.231 5=2.463。且 C03=Cmax=1.481，则 C∑3=C03+Cw3=1.481+2.463=3.944，代入式（12），得弹复曲率比 Cf3=M3=1.647 5，残留曲率比Cc3=Cw3-Cf3=0.815 5。

第四辊以后采用小变形。C04-Cc3=0.815 5，代入式（13），解得 Cw4=1.425 69。原来直的部位（C04=0）被压弯，则将 C∑4=Cw4代入式（12），得 Cf4=M4=1.2527，Cc4=Cw4-Cf4=0.172 99＞0.09 9，未满足要求。 C05=Cc4=0.172 99，代入式（13），得 Cw5=1.252 74。 Cf5=M5=1.1858，Cc5=Cw5-Cf5=0.066 94＜0.099，满足精度要求。考虑到原始弯曲为双向，辊数取为6辊。