模块化多电平变流器稳态运行特性分析

刘 普 王 跃 雷万钧 姚为正

(1.西安交通大学电气工程学院 西安 710000 2.许继柔性输电系统公司 许昌 461000)



模块化多电平变流器稳态运行特性分析

刘 普1王 跃1雷万钧1姚为正2

(1.西安交通大学电气工程学院 西安 710000 2.许继柔性输电系统公司 许昌 461000)

在考虑桥臂电流包含所有次谐波成份的基础上，提出一种新的模块化多电平变流器(MMC)稳态运行特性分析方法。通过研究分析MMC内部各电气变量间的耦合关系，推导得出系统通用矩阵方程，进而得到桥臂电流、子模块电容电压、相间环流等电气变量解析表达式，并总结了各变量稳态运行规律。该方法计算过程相对简单，计算结果更为精确。基于23电平MMC背靠背平台的仿真、实验结果与理论分析结果对比，证明了所提方法的可行性与可靠性。

模块化多电平变流器 稳态 环流 通用矩阵方程

0 引言

模块化多电平变流器因具有易扩展、损耗小、畸变小、可靠性高、便于安装调试和维护等优点，成为目前柔性直流输电领域研究的热点。进行系统主回路参数设计时，需要准确计算并明晰MMC各电气变量运行规律及相互间约束关系；另一方面，在系统主回路参数确定的情况下，对MMC进行稳态运行特性分析有利于控制器参数及系统保护定值的设计。因此，对MMC进行稳态运行特性分析具有重要意义。

文献[1]建立了MMC开关函数模型，列写了交流输出电压与模块开关状态约束方程，便于直观分析单个模块暂态运行特性，但由于开关函数具有显著的非线性特征及高频特性，不利于进行系统稳态特性分析。文献[2]在MMC开关模型基础上，建立了dq坐标系下平均模型，便于进行控制器参数设计。文献[3]给出了MMC应用于无源网络供电时系统建模与控制，但其只考虑了MMC运行的外特性，并未对运行过程中换流器内部各电气变量运行规律及约束关系进行分析。文献[4]只考虑桥臂电流包含直流分量与工频分量时，建立了MMC小信号模型，并推导了MMC开环传递函数和动态响应时间常数。文献[5]不考虑桥臂电流谐波成份，结合开关函数与瞬时功率，得出变流器内部电气变量的解析表达式；由于MMC储能元件分布于各子模块电容中，功率传输必然导致模块电容电压波动，从而引起系统内部环流的产生。文献[3-5]进行系统分析时，忽略了环流成份，简化了系统分析的同时，一定程度上影响了系统分析的准确性。在此基础上文献[6，7]考虑桥臂二次谐波成份，使得变流器内部电气参量的时域解析结果更为准确；但当电容电压波动较大或桥臂电感取值较小时，仅考虑二次环流忽略其他高频次谐波成份将会引起较大偏差。针对这一问题，文献[8]提出一种考虑所有谐波成份的MMC稳态运行特性分析方法，但该方法推导计算过程过于复杂。

系统运行特性分析过程中，以上分析方法及文献[5，8-14]均以MMC电路对称或直接假设交流电流在上、下桥臂中均分为假设条件进行分析，而实际只有上、下桥臂投入模块相同时，电路的瞬时参数才可能对称；并且交流电流在上、下桥臂均分是上、下桥臂充/放电功率瞬时相等的原因而非结果。因此，有必要对交流电流是否在上、下桥臂实时均分进行系统分析。

本文提出一种MMC稳态运行特性分析方法，在考虑桥臂电流包含所有次谐波成份的基础上，详细分析了子模块电容电压、桥臂电流工频、谐波成份、桥臂投入模块电压和稳态运行特性，推导得出了系统通用矩阵方程，通过求解通用矩阵方程可得系统各电气量的解析表达式，并得到上、下桥臂子模块电容电压直流分量相等，交流电流在上、下桥臂均分，相间环流只含偶次谐波成份且所有偶次谐波成份初相角相等等结论，便于深入理解MMC稳态运行特性。以往分析方法大多忽略了桥臂电流的高次谐波成份，或根据仿真、实验中观测到的低次谐波分量在分析研究中加以考虑体现。而本文在建模开始即假设系统包含所有次谐波成份，通过列写系统回路电压方程，分析变量间的约束关系，提取方程等式两端各次频率分量，重构系统方程矩阵，得到系统通用矩阵方程的同时，也得到了系统中应包含的谐波次数及含量。由于考虑了所有次谐波成份，因此，根据该方法得到的理论分析结果更为精确；而且，根据不同的应用场合性能指标要求，可有选择的考虑系统所包含的谐波次数，能够有效平衡系统模型准确性与复杂性之间的矛盾，适用范围更广。

本文搭建了额定传输功率60 kW，额定直流电压2 700 V，23电平MMC背靠背仿真与实验平台，对所提分析方法进行了仿真与实验验证。

1 MMC内部电气参量约束关系

MMC系统原理图如图1所示。该变流器由3个相单元组成，每相含上、下两个桥臂，每个桥臂含桥臂电感L和N个级联子模块。通过调节上、下桥臂投切模块数量以拟合输出正弦交流电压，同时任意时刻每相需投入N个子模块[15]，以维持直流母线电压恒定。

图1 模块化多电平变流器系统原理图Fig.1 The circuit diagram of MMC system

本文采用工程中较常用的最近电平逼近调制(NLM)方式[16，17]，在此基础上进行MMC稳态运行特性分析。鉴于本文的研究目的，作如下假设：

1)假设交流电网为三相理想对称电压源，忽略电网电压畸变。

2)工程应用中MMC模块均衡控制频率足够高，忽略子模块间电容电压差异。

3)忽略子模块、桥臂电感损耗。

4)实际工程中桥臂子模块数量可达数百个，输出的交流电压、电流畸变小，忽略并网电流谐波成份。

以A相为例对MMC进行分析，首先对系统电气变量进行定义。选取A相调制波初相角为零作为研究起始时刻，不失一般性，设A相电流、电压、A相调制波、A相上、下桥臂调制波函数分别为

ia=Iasin(ωt+θ)

(1)

ua=Uasin(ωt+β)

(2)

(3)

(4)

设A相上桥臂电流iap包含所有次频率分量

(5)

式中，a0、an分别为桥臂电流直流分量、n次谐波分量幅值；θn为桥臂电流n次谐波分量初相角。

根据基尔霍夫节点电流方程可得下桥臂电流ian

ian=iap+ia

(6)

定义相间环流izf为

(7)

结合A相上、下桥臂调制波，可分别得出上、下桥臂子模块电容电压为

(8)

式中，upc、unc分别为上、下桥臂子模块电容电压；u0、u1分别为上、下桥臂子模块电容电压初值；C为子模块电容容值。

结合式(8)可求得上、下桥臂投入模块电压和分别为

(9)

2 MMC稳态运行特性分析

2.1 桥臂电流工频分量分析

分别将式(5)、式(6)代入式(8)，可得上、下桥臂子模块电容电压分别为

(10)

(11)

将式(10)上桥臂子模块电容电压展开可得

upc=Ep1+Ep2+Ep3+Ep4

(12)

其中

Ep2=u0

式中，Ep1为t的一次函数，随着t的增大而发散；Ep2为上桥臂子模块电容电压初始值；Ep3、Ep4为关于t的正弦周期函数。同理，式(11)展开可得

unc=En1+En2+En3+En4

(13)

其中

式中，En1为t的一次函数，随着t的增大而发散；En2为下桥臂子模块电容电压初始值；En3、En4为关于t的正弦周期函数。系统稳态运行时，子模块电容电压收敛。因而，Ep1、En1满足以下约束条件

Ep1=En1=0

(14)

联立式(12)～式(14)，化简可得

(15)

由式(15)可知，系统任意运行工况所对应的两矢量满足该等式，即该等式恒成立。由此可得

(16)

将式(16)代入式(6)可得下桥臂电流为

(17)

将式(5)与式(17)代入式(7)可得相间环流表达式

(18)

结论1：

1)由式(16)可知，A相交流电流在上、下桥臂间实时均分。

2)相间环流的存在导致上、下桥臂电气变量(子模块电容电压、电感端电压等)不对称，因此，上、下桥臂电气参数对称只是A相交流电流在上、下桥臂间均分的充分但不必要条件。

3)由式(18)可知，相间环流中不含基波成份。

2.2 子模块电容电压直流分量分析

根据图2所示上、下桥臂投入模块电压和、桥臂电感端电压、交流对地电压、直流对地电压构成的电压回路，分别列写回路电压方程，可得

(19)

(20)

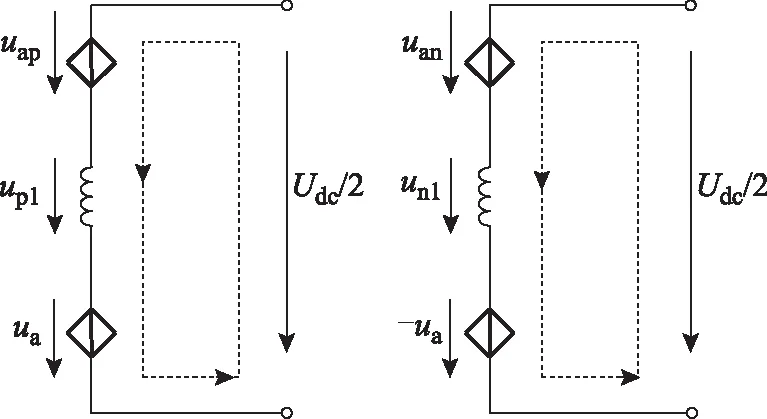
图2 上、下桥臂交、直流回路等效电路图Fig.2 The equivalent circuit diagram of AC-DC loop circuit with upper or lower arm

上、下桥臂电感端电压分别表示为

(21)

(22)

将式(10)、式(11)上、下桥臂子模块电容电压代入式(9)可得上、下桥臂投入模块电压和分别为

(23)

(24)

将式(23)上桥臂投入模块电压和展开为

uap=Eps1+Eps2+Eps3

(25)

其中

式中，Eps1为直流分量，Eps3中当n=2时存在一项直流分量；Eps2、Eps3为周期函数。

同理，将式(24)下桥臂投入模块电压和展开为

uan=Ens1+Ens2+Ens3

(26)

其中

将式(21)上桥臂电感端电压、式(23)上桥臂投入模块电压和代入等式(19)，提取等式两端直流分量可得

(27)

下桥臂同理可得

(28)

联立式(16)、式(27)、式(28)可得

(29)

结论2：

1)由式(29)可得，稳态时上、下桥臂子模块电容电压直流分量相等。

2)子模块电容电压直流分量与系统调制度、桥臂电流工频分量峰值及初相角、二倍频电流峰值及初相角相关，即子模块电容电压直流分量随系统运行工况不同而波动。

2.3 相间环流谐波分量分析

根据图3所示上桥臂投入模块电压和、上桥臂电感端电压、下桥臂投入模块电压和、下桥臂电感端电压、直流母线电压构成的直流回路，列写基尔霍夫电压方程

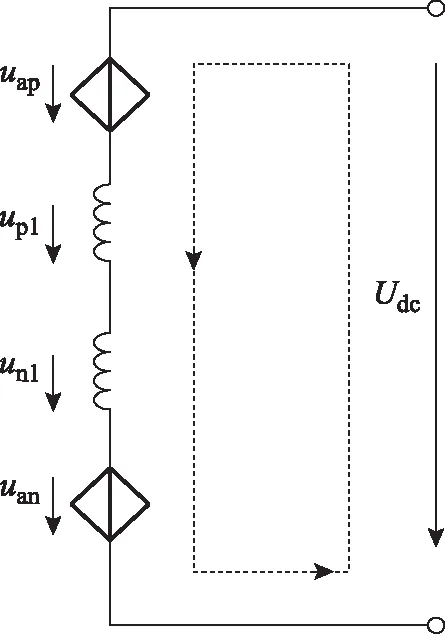
图3 直流回路等效电路图Fig.3 The equivalent circuit diagram of DC loop circuit

(30)

由直流回路电压方程(30)及结论1可得

(31)

结合式(25)、式(26)可得

uap+uan=Epns0+Epns1+Epns2+Epns3+Epnsn

(32)

其中，直流分量表达式为

基波分量表达式为

二次分量表达式为

三次分量表达式为

n次分量表达式为

由结论1可知，相间环流izf不含工频分量，由此可推得等式(31)左右两端均不含工频分量，即式(32)工频分量等于零

(33)

由式(33)可得

a3=0

(34)

由式(34)可得，桥臂电流不含3次谐波成份，即等式(31)左右两端均不含3次谐波成份，可得

(35)

结合式(34)可得

a5=0

(36)

不失一般性，设a1=a3=…=a2k+1=0， 则式(31)两端均不含2k+1次谐波成份，则式(31)左端的2k+1次分量可表示为

(37)

将a1=a3=…=a2k+1=0代入式(37)可得

(38)

进而可得

a2k+3=0

(39)

因此可得

a2k+1=0k∈(1,+∞)

(40)

对桥臂电流偶次谐波成份作进一步分析。由式(31)两端2k次谐波含量相等可得

(41)

变流器稳态运行时，式(41)中当k→+∞， 可得

a2k+2=0k→+∞

(42)

则式(41)可化简为

(43)

由式(43)可得

θ2k=θ2k-2

(44)

同理，将式(44)代入式(41)递推可得

θ2k=θ2k-2=…=θ4=θ2

(45)

结论3：

1)由式(40)可得桥臂电流及相间环流中不含奇次谐波成份。

2)由式(45)可得桥臂电流及相间环流中偶次谐波成份初相角相等。

综上所述，桥臂电流可化简为

(46)

2.4 系统通用矩阵方程

结合结论1～3，将上、下桥臂电流表达式(46)代入式(31)，并提取式(31)各次频率分量，重构系统矩阵方程可得

BX=A

(47)

式中

XT={a2,a4, …,a2n}

AT={k, 0, 0, 0, 0}

由系统矩阵B可知，该矩阵为n×n阶对称方阵，且该矩阵的秩不为零，因此该方程组线性无关，方程组(47)的解存在且惟一。将系统参数代入矩阵方程，即可求得桥臂电流解析表达式，从而进一步可求得子模块电容电压、桥臂电流、投入模块电压和等电气量解析表达式，为MMC稳态运行特性分析奠定了理论基础。

3 仿真研究

为验证本文所提出的MMC稳态运行特性分析方法的有效性，基于Matlab/Simulink搭建了如图4所示23电平MMC背靠背仿真模型。

图4 MMC背靠背仿真系统原理图Fig.4 The simulation diagram of MMC back-to-back system

系统仿真参数设置如表1所示。

表1 MMC背靠背系统参数表Tab.1 Parameter table of MMC back-to-back system

选取MMC1交流侧向直流侧传输P=0.5 pu即30 kW有功功率；Q=0.85 pu即补偿系统51 kvar容性无功作为系统研究工况。采用本文MMC稳态运行特性分析方法，将表1所示主回路参数代入系统通用矩阵方程(47)，求解该方程可得MMC内部各电气变量解析表达式。图5所示为该工况下桥臂电流、子模块电压理论分析与仿真结果对比波形。其中图5所示“全频”波形代表包含所有次谐波成份的电压、电流仿真波形；“工频”波形表示仅考虑工频分量的电压、电流理论分析波形；“二次”波形表示考虑工频、2次分量的电压、电流理论分析波形；“4次”波形表示考虑4次及以下次谐波成份的电压、电流理论分析波形；“10次”波形表示考虑10次及以下次谐波成份的电压、电流理论分析波形。由式(47)可知，考虑谐波的次数越高，待求解的系统通用矩阵方程阶数越高，计算量越大。由图5可知，4次理论分析波形与仿真结果已经高度吻合，满足实验系统准确度要求，因此，本文后续仿真、实验中仅考虑4次谐波成份，忽略其他高次谐波成份。

图5 理论分析与仿真结果对比Fig.5 Theoretical analysis and simulation result comparison

求解式(47)可得上桥臂电流、上桥臂子模块电压、上桥臂投入模块电压和表达式分别为

(48)

进一步提取桥臂电流与子模块电容电压各次分量，进行仿真结果与理论分析对比，如表2所示。

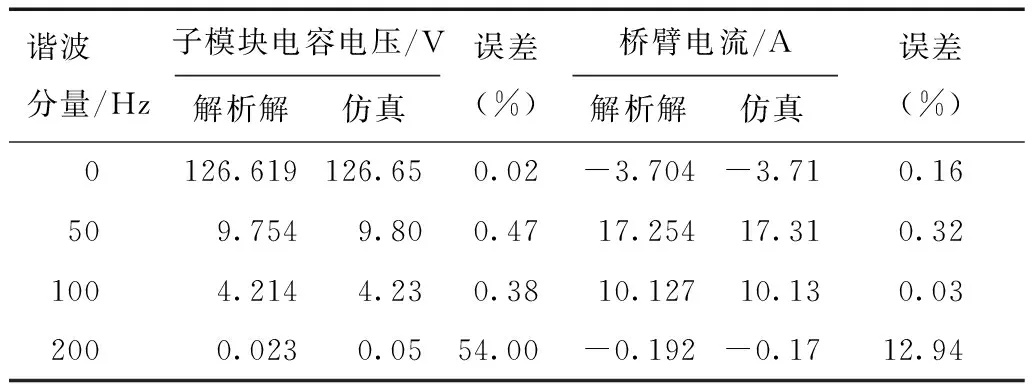
表2 仿真结果与解析解分析对比Tab.2 Comparison of simulation result and analytical result

由表2理论分析结果与仿真结果对比表明，基于MMC稳态运行特性解析结果能够准确反映系统运行特性以及谐波对系统的影响。桥臂电流工频分量、子模块电容电压直流分量、桥臂电流谐波分量的仿真结果分别证明了结论1～3的正确性。其中由于电压、电流4次谐波基值较小，而桥臂模块数量有限导致NLM调制带来的谐波影响以及测量误差影响，使得电压、电流4次谐波含量分析误差相对较大。鉴于工程中MMC连接电网电压等级高，模块数量多达上百个，因此，由于调制所带来的谐波含量可忽略不计。

4 实验研究

本文搭建了23电平MMC背靠背动模实验系统，对MMC稳态运行特性分析方法进行实验验证。图6为MMC背靠背实验系统实物图，主要由电网、变压器、功率模块柜、极控柜、阀控柜及测量系统构成。实验系统参数如表1所示。

图6 MMC背靠背动模实验平台Fig.6 MMC back-to-back dynamic test system

为了便于进行实验结果与理论分析对比，选取与仿真同样的工况进行实验。图7为稳态时子模块电容电压、桥臂电流、上桥臂投入模块电压和、阀侧交流电压的实验波形。

图7 MMC稳态输出波形Fig.7 The steady-state waveform of MMC

为了更直观地进行理论分析结果与实验结果对比，将实验数据与解析解同时导入Matlab，如图8所示，并分别对子模块电容电压、桥臂电流实验结果进行傅里叶变换分析，与理论分析结果对比见表3。

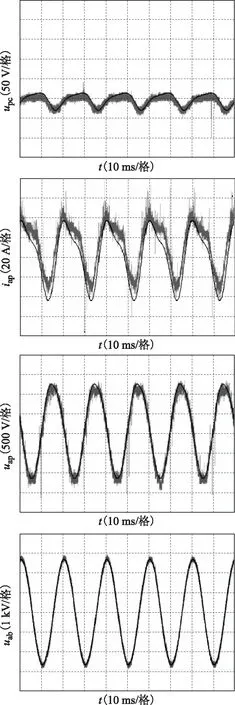
图8 实验结果与解析结果对比波形Fig.8 The comparison of experimental and analytical results

谐波分量/Hz子模块电容电压/V解析解仿真误差(%)桥臂电流/A解析解仿真误差(%)0126.620127.200.46-3.704-3.823.04509.75410.012.5617.25417.873.451004.2144.353.1210.12710.574.192000.0230.1382.30-0.192-0.3138.10

由图8及表3可知，理论分析结果与实验结果总体吻合，其中模块电压、桥臂电流的直流、工频、二次含量解析解与实验结果间最大误差小于5%，证明了本文中推导结论1～3的正确性。其中由于4次谐波成本本身基值较小，实验过程中变流器损耗、电网背景谐波及测量装置准确度导致模块电压、桥臂电流的4次谐波成份实验结果与理论分析误差较大。

5 结论

在考虑桥臂电流包含所有次谐波含量基础上，提出了一种MMC稳态运行特性分析方法。基于该方法推导了系统通用矩阵方程，通过求解该矩阵方程，可得到MMC内部各电气量解析解，从而为系统运行特性分析及主回路参数设计提供了理论依据。仿真与实验结果证明了所提方法的可行性与可靠性；同时，通过MMC稳态运行特性分析，可得如下结论：

1)首次给出了MMC交流工频电流在上、下桥臂实时均分的理论依据。

2)桥臂电流与相间环流中只含偶次谐波成份，且所有偶次谐波电流初相角相等；相间环流不含奇次谐波成份。

3)稳态运行时上、下桥臂子模块电容电压直流分量相等，幅值随系统运行工况不同而波动。

[1] Solas E，Abad G，Barrena J A，et al.Modeling simulation and control of modular multilevel converter[C].Power Electronics and Motion Control Conference (EPE/PEMC)，Ohrid，Macedonia，2010：90-96.

[2] Zhao Yan，Hu Xuehao，Tang Guangfu，et al.A study on MMC model and its current control strategies[C].2010 2nd IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG)，Hefei，China，2010：259-264.

[3] 管敏渊，徐政.向无源网络供电的MMC型直流输电系统建模与控制[J].电工技术学报，2013，28(2)：255-263. Guan Minyuan，Xu Zheng.Modeling and control of modular multilevel converter based on VSC-HVDC system connected to passive networks[J].Transactions of China Electrotechnical Society，2013，28(2)：255-263.

[4] 刘栋，汤广福，郑建超，等.模块化多电平换流器小信号模型及开环响应时间常数分析[J].中国电机工程学报，2012，32(24)：1-7. Liu Dong，Tang Guangfu，Zheng Jianchao，et al.Small signal modeling and analysis of open-loop response time constant of MMC[C].Proceedings of CSEE，2012，32(24)：1-7.

[5] 王姗姗，周孝信，汤广福，等.模块化多电平电压源换流器的数学模型[J].中国电机工程学报，2011，31(24)：1-8. Wang Shanshan，Zhou Xiaoxin，Tang Guangfu，et al.Modeling of modular multi-level voltage source converter[J].Proceedings of CSEE，2011，31(24)：1-8.

[6] 宋强，刘文华，李笑倩，等.模块化多电平换流器稳态运行特性的解析分析[J].电网技术，2012，36(11)：198-204. Song Qiang，Liu Wenhua，Li Xiaoqian，et al.An analytical method for analysis on steady-state operating characteristics of modular multilevel converter[J].Power System Technology，2012，36(11)：198-204.

[7] 张建坡，赵成勇.模块化多电平换流器环流及抑制策略研究[J].电工技术学报，2013，28(10)：328-336. Zhang Jianpo，Zhao Chengyong.Research on circulating current and suppressing strategy of modular multilevel converter[J].Transactions of China Electrotechnical Society，2013，28(10)：328-336.

[8] Ilves K，Antonopoulos A，Norrga S，et al.Steady-state analysis of interaction between harmonic components of arm and line quantities of modular multilevel converters[J].IEEE Transactions on Power Electronics，2012，27(1)：57-68.

[9] 王姗姗，周孝信，汤广福，等.模块化多电平HVDC输电系统子模块电容值的选取和计算[J].电网技术，2011，35(1)：26-32. Wang Shanshan，Zhou Xiaoxin，Tang Guangfu，et al.Selection and calculation for sub-module capacitance in modular multi-level converter HVDC power transmission system[J].Power System Technology，2011，35(1)：26-32.

[10]Tu Qingrui，Xu Zheng，Xu Lie.Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters[J].Power Delivery，IEEE Transactions on，2011，26(3)：2009-2017.

[11]屠卿瑞，徐政，郑翔，等.模块化多电平换流器型直流输电内部环流机理分析[J].高电压技术，2010，36(2)：547-552. Tu Qingrui，Xu Zheng，Zheng Xiang，et al.Mechanism analysis on the circulating current in modular multilevel converter based HVDC[J].High Voltage Engineering，2010，36(2)：547-552.

[12]屠卿瑞，徐政，管敏渊，等.模块化多电平换流器环流抑制控制器设计[J].电力系统自动化，2010，34(18)：57-61，83. Tu Qingrui，Xu Zheng，Guan Minyuan，et al.Circulating current suppressing controller designing for modular multilevel converter[J].Automation of Electric Power System，2010，34(18)：57-61，83.

[13]丁冠军，丁明，汤广福，等.新型多电平VSC子模块电容参数与均压策略[J].中国电机工程学报，2009，29(30)：1-6. Ding Guanjun，Ding Ming，Tang Guangfu，et al.Submodule capacitance parameter and voltage balancing scheme of a new multilevel VSC modular[J].Proceedings of CSEE，2009，29(30)：1-6.

[14]Antonopoulos A，Angquist L，Nee H P.On dynamics and voltage control of the modular multilevel converter[C].13th European Conference on Power Electronics and Applications，Barcelona，2009：1-10.

[15]Nademi H，Das A，Norum L.An analytical frequency-domain modeling of a modular multilevel converter[C].2012 3rd Power Electronics and Drive Systems Technology (PEDSTC)，Tehran，2012：86-91.

[16]管敏渊，徐政，屠卿瑞，等.模块化多电平换流器型直流输电的调制策略[J].电力系统自动化，2010，34(2)：48-52. Guan Minyuan，Xu Zheng，Tu Qingrui，et al.Modulation strategy of modular multilevel converter based HVDC[J].Automation of Electric Power System，2010，34(2)：48-52.

[17]屠卿瑞，徐政，郑翔，等.一种优化的模块化多电平换流器电压均衡控制方法[J].电工技术学报，2011，26(5)：15-20. Tu Qingrui，Xu Zheng，Zheng Xiang，et al.An optimized voltage balancing method for modular multilevel converter[J].Transactions of China Electrotechnical Society，2011，26(5)：15-20.

Analysis of Steady-State Operating Characteristics for Modular Multilevel Converters

LiuPu1WangYue1LeiWanjun1YaoWeizheng2

(1.School of Electrical Engineering Xi’an Jiaotong University Xi’an 710000 China 2.Xuji Flexible Transmission System Corporation Xuchang 461000 China)

Considering all the harmonic components for the arm current，this paper proposes a new steady-state operation characteristic analysis method for the modular multilevel converter(MMC).Based on the analysis of the coupling relationship among the internal electric variables of MMC，the general matrix equation of the system is derived and the analytical expression of the arm current，submodule capacitor voltage and circulating current is obtained，and then the operation law of these variables is concluded.The calculation process is relatively simpler and the analysis results are more accurate with this method.The simulation and experimental results based on 23-level MMC back-to-back platform are compared to the analytical results，respectively.It verifies that the proposed method is feasible and accurate.

Modular multilevel converter，steady-state，circulating current，general matrix equation

国家高技术研究发展(863)计划(2012AA050206)资助项目。

2015-01-14 改稿日期2015-04-02

TM46

刘 普 男，1984年生，博士研究生，研究方向为柔性直流输电技术。(通信作者)

王 跃 男，1972年生，教授，博士生导师，研究方向为大功率电力电子变换技术。