基于小波变换和ROF模型的图像去噪算法

王利娜，何文章，李长领，梁 婕

（1.天津职业技术师范大学理学院，天津 300222；2.天津职业技术师范大学汽车与交通学院，天津 300222）

基于小波变换和ROF模型的图像去噪算法

王利娜1，何文章1，李长领2，梁 婕1

（1.天津职业技术师范大学理学院，天津 300222；2.天津职业技术师范大学汽车与交通学院，天津 300222）

小波变换和ROF模型是常用的图像去噪方法。为了获取高质量图像，降低或消除噪声对图像的影响，提出了一种新的图像去噪算法。该方法对噪声图像进行小波分解，并对其高频部分进行阈值去噪，之后利用ROF和拉普拉斯算子结合的模型去噪，并进行小波重构，得到最终的去噪图像。实验结果表明，此算法的去噪效果比小波去噪或ROF去噪明显，能在有效抑制图像噪声的同时，更好地保持图像的边缘、纹理等特征，有效地提高了图像质量。

图像去噪；小波变换；ROF模型；拉普拉斯算子

图像在传输、转换和存储过程中，会产生一定的失真，造成图像质量下降，典型的表现为图像模糊、含有噪声等，噪声的产生为图像的进一步处理增加了困难。因此，为了抑制噪声，改善图像质量，对含有噪声的图像进行图像去噪就显得尤为重要。传统的图像去噪方法主要有2大类，分别是空域滤波和频域滤波，这些方法主要是通过滤除图像的高频成分来达到去除噪声的目的。由于这些方法主要是对图像整体信息进行处理，很容易将图像的一些细节信息滤除，导致恢复图像看起来比较模糊，处理效果不够理想。20世纪90年代以来，使用偏微分方程（PDE）进行图像处理的方法获得了较大的发展，其中最著名的就是Rudin、Osher和Fatemi提出的基于全变分的图像去噪模型（ROF模型）[1]，该模型可以很好地保持边缘信息和抑制图像的噪声，但是该模型在去噪过程中运算量大，运算效率不如传统图像去噪方法且在图像去噪后容易产生阶梯效应。近年来，小波理论得到了快速发展，很多学者也应用小波进行降噪，获得了较好的效果。但由于小波变换不具有平移不变性，所以直接用小波变换降噪得到的降噪图像存在Gibbs效应[2]。目前对ROF模型和小波变换的联合去噪方法还很少，本文基于ROF模型与小波变换的算法，首先建立了ROF模型和拉普拉斯算子的联合去噪模型（简称RL模型），然后经小波变换对图像高频进行阈值去噪后，对其高频分量进行RL模型去噪，最后再经小波重构得到最终去噪图像。本文方法克服了单纯运用小波变换或ROF模型的不足，能够在保持图像边缘等信息的同时，达到良好的去噪效果。

1 小波变换和ROF模型去噪原理

1.1 小波变换去噪原理

近年来，小波理论得到快速发展，由于其具备良好的时频特性，因而实际应用非常广泛。在降噪领域中，很多学者也应用小波进行降噪，获得了良好效果。在数学上，小波去噪问题本质是一个函数逼近问题，是通过在小波母函数伸缩和平移所张成的函数空间中，根据所给出的衡量准则，寻找出对原始信号的最佳逼近，以完成原信号和噪声信号的区分[3]。小波去噪是特征提取和低通滤波功能的综合，其去噪过程如图1所示。

图1 小波变换去噪过程

目前，基于阈值收缩的小波降噪方法的研究非常活跃[4-5]，并且阈值收缩方法在去除高斯白噪声方面取得了很大成功。本文设定图像噪声为高斯白噪声，选用阈值收缩的方法进行图像去噪。该方法的关键在于确定阈值和阈值函数。对于确定阈值的方法，引用1992年Donoho等[4]提出的小波阈值收缩方法。这种方法从某种渐进意义上证明了该阈值的最优性，此方法给出了阈值公式为:

Bruce等[6]在高斯白噪声条件下，得到了软阈值和硬阈值收缩方法的偏差、方差、L2风险公式及其结论。通过对比分析，本文选用软阈值方法进行处理，软阈值相对于硬阈值处理结果较为平滑，造成的伪“Gibbs”效应相对较小。软阈值方法表达式如下:

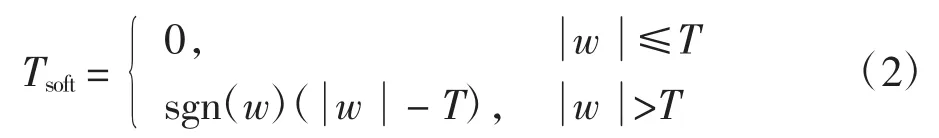
1.2 ROF模型去噪原理

ROF模型是1992年由Rudin等[1]提出的基于全变分思想的方法模型，其基本思想是带有噪声的图像的总变分总是大于没有噪声的图像的总变分。ROF模型的数学表达式如下:

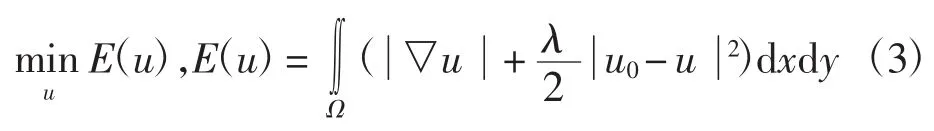
式中:u为原始图像；u0为带噪声图像；▽u为梯度算子；为梯度算子的模；λ为约束参数，且λ≥0。当λ=0时，式（3）为总变分公式（TV）式（3）中部分是对图像能量的估计，起到平滑作用，称为正则项；这部分表示恢复的图像u与噪声图像u0的差别，称为保真项，即使恢复前后的图像保持在一定的差别之内。λ起到平衡正则项与保真项的作用，λ值越大，恢复的图像u越接近u0[7]。

ROF模型表达式的欧拉—拉格朗日方程为:

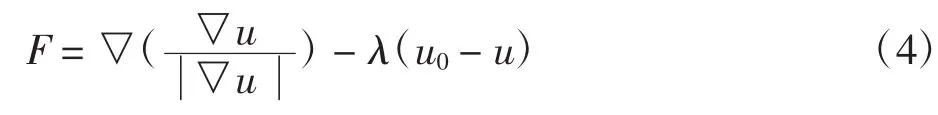
对于约束参数λ的选择，由于选择常数作为约束参数的方法仅适用于噪声规模较小的图像，这里采用在文献[1]中给出的计算方法，λ的计算为:

其中，设定第一次迭代λ=0。这种方法在每次迭代过程都进行更新，使得每次去噪过程对λ的选择更加合适，得到的结果也更加理想。

2 联合去噪算法

小波变换与ROF模型在去噪过程中各有其优点，但只运用小波去噪在重构图像后容易产生Gibbs现象，只进行ROF模型去噪后容易产生阶梯效应，因此可以把两者结合起来，在图像去噪中发挥各自的优势，从而在去除噪声的同时，达到提升图像质量的目的。

由于含噪图像的噪声主要集中在图像的高频部分，所以首先对图像进行小波变换分解，只对高频分量进行阈值处理，然后对高频分量运用ROF模型算法去噪，最后进行小波重构得到去噪图像。通过小波去噪，图像的大部分噪声将会被消除，这样再运用ROF模型进行去噪，即可有效减少或避免直接进行ROF去噪产生的阶梯效应。由于噪声图像经过多次小波变换后图像会逐渐变得模糊，而ROF模型对图像去噪的同时具有保真项的约束，对图像的保真程度相对较好，所以对噪声图像只运用一次小波变换进行去噪，保证大部分噪声被滤除即可。但即便如此，图像的边缘仍然会受到一定的影响，因此有必要对图像进行锐化处理。拉普拉斯锐化能在保留图像基本信息的基础上，使图像细节显现出来。拉普拉斯锐化是利用拉普拉斯算子对图像进行边缘增强的一种方法，其基本思想为:当邻域的中心像素低于它所在的邻域内其他像素的平均灰度时，此中心像素的灰度应该进一步降低，反之同理，依此实现对图像的锐化处理。

利用加权系数把ROF模型与拉普拉斯算子的模型相结合，得到新的去噪模型（简称RL模型），从而使ROF模型去噪与拉普拉斯锐化同时进行，RL模型表达式如下:

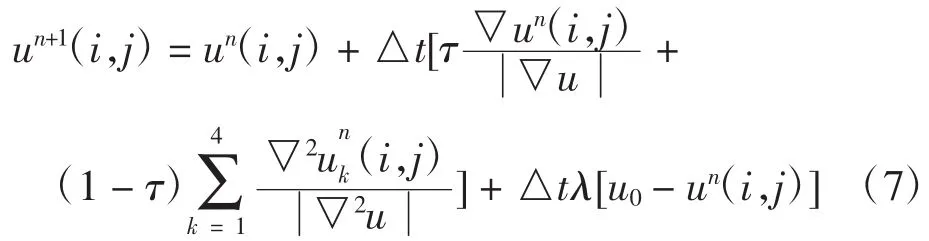
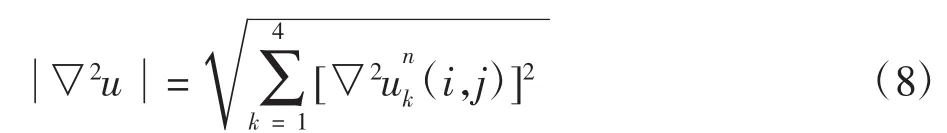
本文算法的主要步骤如下:

（1）对噪声图像进行小波分解。

（2）对小波分解后的3个高频分量分别进行采用软阈值方法进行阈值处理，阈值的确定根据式（2）计算。

（3）对经过阈值处理后的3个高频分量运用RL模型算法去噪，采用迭代运算，直到收敛；其中RL模型具体步骤为:

i.初始化各参数，τ、△t、迭代收敛值ε、n=0、ROF正则项R=u0、拉普拉斯算子L=u0，执行下一步；

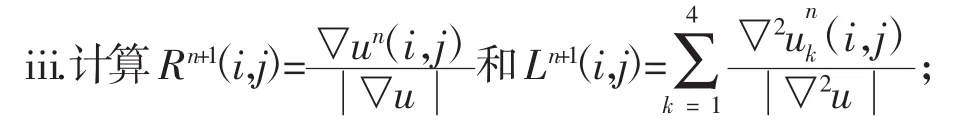
iv.根据式（6）计算λ，并带入式（7）计算un+1（i，j），令Rn+1（i，j）=Ln+1（i，j）=un+1（i，j），返回ii。

（4）通过小波重构得到去噪图像。

3 实验结果与分析

通过对各种小波去噪效果的实验比较，本文选用sym4小波进行小波变换。研究选用加入噪声方差为20的Cameraman图像进行实验，对RL模型权值的选取，通过仿真实验，设置权值改变步长为0.01。经过对实验结果的综合分析，选取权值τ=0.88。去噪的处理结果如图2所示。为了更清晰地比较去噪效果，文中显示了去噪后的局部效果，如图3所示。

图2 Cameraman图像去噪结果比较

图3 Cameraman图像局部去噪结果比较

为验证本文算法的有效性，采用峰值信噪比（PSNR）和最小均方差（MSE）进行检验，处理结果如表1和表2所示。

表1 图像去噪后的PSNR

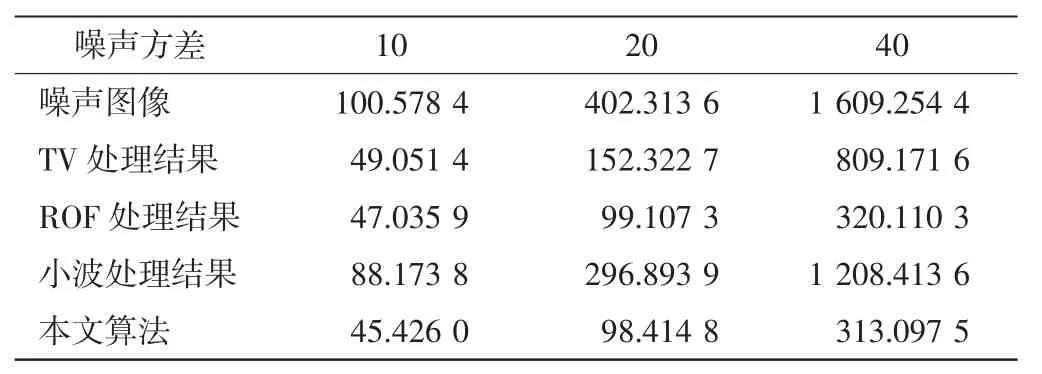
表2 图像去噪后的MSE

表1为Cameraman分别加入方差为10、20、40噪声后各种方法去噪后的PSNR，表2为Cameraman分别加入方差为 10、20、40噪声后各方法去噪后的MSE。从表1和表2中可以看出，本文算法比其他算法PSNR有一定程度上的增加，同时MSE也相对较小，而且噪声方差越小，本文算法相对其他几种算法的去噪效果更好。

从以上实验结果看，几种算法都能去除一定的噪声，但是去除噪声的效果差异很大。从图2可以看出，在去除噪声方面，TV模型和小波阈值处理明显不如ROF模型和本文算法。进一步从图3局部去噪效果可以看出，ROF模型去噪效果明显，平滑效果和边缘保持都比较好，但是图像存在一定的阶梯效应；本文算法和ROF模型相比，阶梯效应明显减弱，同时也有效地抑制了Gibbs现象。

4 结束语

小波变换和ROF模型是图像去噪的2种常用方法，本文通过分析其特点，针对其不足，提出了一种结合小波变换和ROF模型的算法，而且为了抑制去噪过程中造成的图像模糊，在ROF模型去噪的同时加入拉普拉斯算子进行锐化，构建ROF和拉普拉斯算子的联合去噪模型（RL模型）。实验结果表明，本文算法能够克服单纯利用小波变换去噪产生的Gibbs效应和ROF模型去噪产生的阶梯效应，能够更有效地去除噪声，保持图像的边缘、纹理等特征，具有很好的去噪效果。

［1］RUDIN L，OSHER S，FATEMI E.Nonlinear total variation based noise removal algorithms［J］.Phys D，1992，60:259-268.

［2］COIFMAN R R，DONOHO D L.Translation Invariant Denoising［M］.New York:Springer-Verlag，1994.

［3］肖志云.小波域数字图像建模及其应用［M］.北京:北京理工大学出版社，2014.

［4］DONOHO D L，JOHNSTONE I M.Ideal spatial adsptation by wavelet shrinkage［J］.Biometrika，1994（8）:425-455.

［5］JOHNSTONE I M，SILVERMAN B W.Wavelet threshold estimators for data with correlated noise［J］.Journal of Royal Statistics Society Series（B），1997，59:319-351.

［6］BRUCE A G，GAO H Y.Understanding waveshrink:variance and bias estimation［EB/OL］.［2015-03-14］.http://www. mathsoft.com/wavelet.html.

［7］胡学刚，张龙涛，蒋伟.基于偏微分方程的变分去噪模型［J］.计算机应用，2012（7）:1879-1881.

［8］王际朝，李维国.一种基于Lp范数的自适应图像去噪模型［J］.中国石油大学学报:自然科学版，2008（2）:155-158.

Image denoising algorithm based on wavelet transform and ROF model

WANG Li-na1，HE Wen-zhang1，LI Chang-ling2，LIANG Jie1
（1.School of Science，Tianjin University of Technology and Education，Tianjin 300222，China；2.School of Automotive and Transportation，Tianjin University of Technology and Education，Tianjin 300222，China）

Wavelet transform and ROF model are common methods for image denoising.In order to keep maximum image edge and other important information while suppressing the noise,a new denoising algorithm is proposed in this paper.Firstly,the noisy image is decomposed using wavelet transform,then each detail image is first denoised with threshold method. Secondly,they are denoised by the model combined with ROF and the laplacian operator.Finally the denoised image is obtained from wavelet reconfiguration.The experimental results show that the proposed algorithm performs better than traditional methods of eliminating noise,and maintain the edge texture characteristic of the image nicely.

image denoising；wavelet transform；ROF model；Laplacian

TP391.41

A

2095－0926（2015）02－0039－04

2015-04-29

天津市应用基础及前沿技术研究计划项目（12JCYBJC10600）.

王利娜（1987—），女，硕士研究生；何文章（1961—），男，教授，硕士生导师，研究方向为系统决策与优化、小波分析及应用.