捷联惯导系统在声振综合环境下的动力学响应特性研究

姚建军，余盛强，甄 瑞，闫红松，殷增振，刘志军

（北京自动化控制设备研究所，北京100074）

捷联惯导系统在声振综合环境下的动力学响应特性研究

姚建军，余盛强，甄 瑞，闫红松，殷增振，刘志军

（北京自动化控制设备研究所，北京100074）

随着导弹等航天器飞行速度的提高，环境噪声的影响已不容忽视，声振综合环境将成为惯导系统等弹上电子设备通常需要面对的力学环境条件。文章论证了有限元法适用于对捷联惯导系统这类结构紧凑型设备进行宽频域声振耦合计算，仿真计算了捷联惯导系统声振耦合模型在声振综合环境下的动力学响应，对比分析了捷联惯导系统在声振综合环境下与在单独随机振动环境、单独噪声场环境下动力学响应的联系、区别以及自身新的特点。研究结论可为设计和评估地面力学环境试验、预示与分析惯导系统在综合环境下的环境适应性提供理论依据。

捷联惯导系统；综合环境；声振耦合；动力学响应

0 引言

导弹等航天飞行器在发射飞行过程中，舱内电子设备会受到发动机推进系统诱发的低频（0Hz～2000Hz）随机振动环境以及气动噪声引起的宽频（10Hz～10kHz）声振激励环境的影响。对于低速航天器，声振环境对舱内电子设备的影响远远弱于低频振动环境。随着飞行速度的提高，特别是在航天器再入大气层超高速飞行时产生的气动噪声的影响已非常显著。对于高速航天器，随机振动与噪声激励的综合作用是其面临的主要力学环境。为确保飞行试验成功，美国NASA通常在产品研制的不同阶段，对部件、分系统、系统均要进行声振环境的鉴定试验。我国对航天器力学环境试验历来重视，军用装备的随机振动试验和噪声试验均有严格的要求和明确的规定。由于条件所限，目前还主要是对试件分别进行单项的随机振动和声场环境试验，忽略了声与振的复合影响，不能真实验证高速航天器在综合环境激励下的环境适应性。

惯导系统作为导弹等航天飞行器的关键子系统，其内部的惯性器件容易受到外部力学环境的干扰和破坏，对力学环境的舒适度要求较高，通常被认为是研究航天飞行器舱内电子设备力学环境适应性的典型代表。文章以一款具有典型结构形式的光学捷联惯导系统为研究对象，采用数值模拟方法，仿真计算了该惯导系统在典型声振综合环境下的动力学响应特性，对比分析了惯导系统在声振综合环境下与在单独随机振动环境、单独噪声场环境下动力学响应特性的联系与区别。由于所研究的捷联惯导系统无论是模块构成还是结构形式、外形尺寸等诸方面都反映了当前国内光学捷联惯导系统的基本情况，从结构动力学角度来看具有较强的代表意义，因此认为，本文研究方法和结论对于捷联惯导系统的研制具有较高的普适价值，可以为设计和评估地面力学环境试验、预示与分析惯导系统在综合环境下的环境适应性提供理论依据。此外，本文工作对于研究航天器舱内电子设备力学环境适应性也具有一定的参考价值。

1 求解惯导系统声振耦合问题的数值方法及其理论基础

惯导系统在噪声激励下产生振动，结构振动同时对环境声场产生影响，环境声场与结构位移场紧密耦合在一起，即通常所谓的声振耦合。声振耦合问题的数值模拟方法主要有统计能量法和有限元法两种。统计能量法的基本原理是将一个复杂系统（包括机械和声学的系统），以模态（振型）相似、自然边界等准则划分成不同的模态群，并从统计意义上把大系统分解成为若干个便于分析与管理的独立子系统，每一个子系统模拟成一组相同解耦模态的振子，根据输入到子系统的能量等于子系统耗散的能量加上子系统间传递的能量，建立表征各子系统的能量损耗与输入功率相互关系的线性方程组（称之为能量流平衡方程），解出该方程组，便可得到每一个子系统所具有的平均能量。统计能量法在求解大结构、复杂装配结构时具有独特的优势，其计算速度快，在高频部分（一般认为在模态密度大于3时）的计算结果更接近真实情况，相比传统有限元方法不受结构离散时奇异性、不连续性的影响，整个分析过程更高效、简单。但统计能量法给出的是空间和频域的统计平均量，得不到系统特殊位置上和特殊频率点处的详细信息。当结构模态密度较小（一般取0.2）时会产生较大的计算误差。惯导系统结构紧凑、刚度较大，即使在10kHz附近的高频区域其模态密度也不足0.2（后文有验证）。其次，利用平均能量来表征结构的力学响应不仅不利于考察易损器件的承载状况，而且也不利于识别结构设计的薄弱环节，所以，统计能量法不适合用于惯导系统的声振环境适应性预计与仿真分析。

有限元法是基于波动方程的数值模拟方法,它能够准确地求解中低频段的各种声学和结构振动问题,而且可以求出所关心节点处的响应。一般认为它不适合用于求解高频问题，理由是：需要巨大的计算资源，计算效率低；在高频处模态密集，计算结果对结构参数的各种不确定性因素非常敏感，计算精度难以保证。当前，计算机的计算能力已得到显著提升，一台PC机就可以具备128G内存、8核并行处理的计算能力，计算能力及计算效率已不成问题。其次，惯导系统结构紧凑、高频模态密度低于0.2，结构设计参数的不确定因素较少，对有限元高频计算精度影响有限。因此认为，有限元法适用于对惯导系统进行全频域力学环境（包括声振问题）的仿真计算。本文的计算即采用有限元方法。下面简要说明求解声振耦合问题有限元法的基本原理。

声振动作为一个宏观的物理现象，其满足的三个基本物理方程（动量方程、连续方程和物态方程）在四个假设条件下得到其波动方程式。建立声学波动方程的基本假设是：①媒质是理想流体，声波在其中传播没有能量损耗；②媒质是均匀的，其静态压强、静态密度都是常数，没有声扰动时，媒质在宏观上是静止的；③声传播过程是绝热的；④媒质中传播的是小振幅声波，各声学量都是一级微量，即声压远小于静态压强，质点振动速度远小于声传播速度，质点位移远小于波长，媒质密度增量远小于静态密度。

利用Galerkin法离散波动方程得到单元矩阵。式（2）乘以一个虚压力并在整个体积域内积分，经过适当变换可以得到

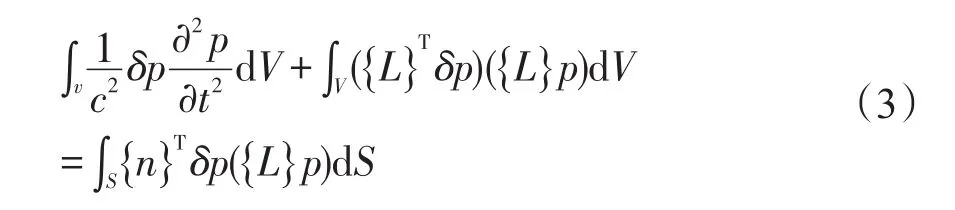
式中：V—流体域的体积；S—流体域的表面；δp—虚压力；n—S面的法向矢量。

在声振耦合问题中，S是对应的声流体与固体结构的分界面。根据前提假设，由流体动量方程可以推导出流固界面上结构法向加速度和流体法向压力梯度之间的关系如下

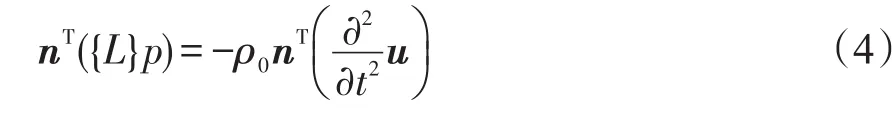
式中u为结构位移矢量。

把式（4）带入式（3）得到

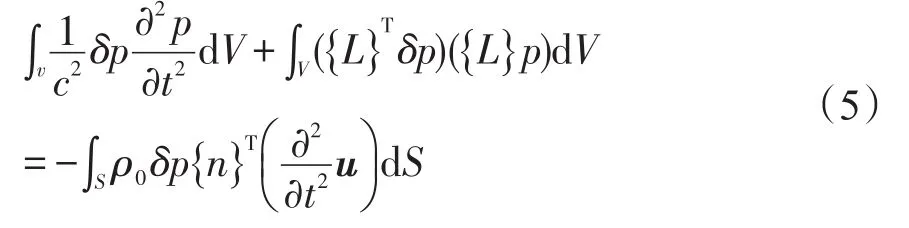
将流体压力P和结构位移矢量u用有限单元节点压力矢量Pe、压力的单元形状函数{N}以及节点位移矢量ue、位移的单元形状函数{N′}近似表示为：

将式（6）、式（7）带入式（5）得到

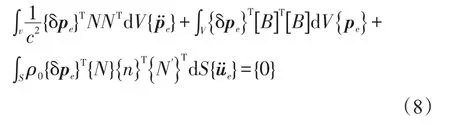
式中B={L}{N}T

整理式（8）得到

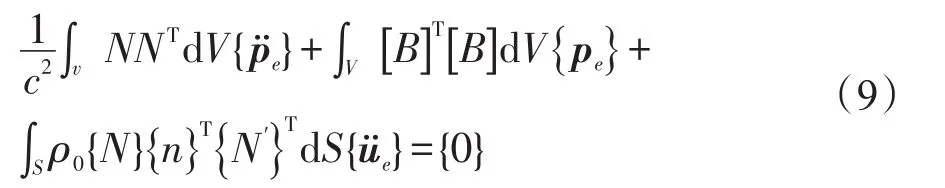
把式（9）表示为矩阵形式，即可得到离散化的波动方程式

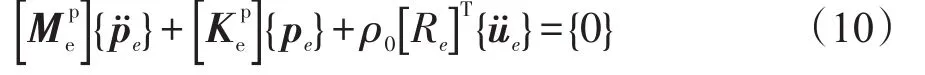
如果考虑流体边界上由于阻尼造成的能量耗散，则波动方程变为

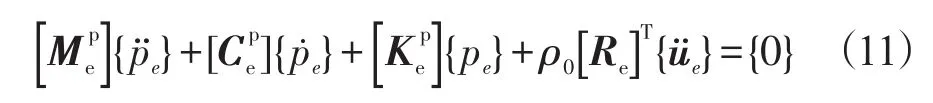
在流固耦合问题中，还需要将流固边界上的流体压力载荷增加到结构体的动力学方程中，

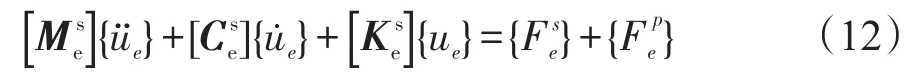
将方程式（11）、式（12）合并在一起，得到声与结构的耦合动力学方程组

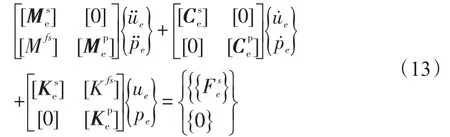
式中：[Mfs]=ρ0[Re]T，[Kfs]=-[Re]

求解该方程组，得到声场压力{p}和结构位移{u}。

2 捷联惯导系统的声振耦合动力学模型

捷联惯导系统的典型结构形式是在一个六面体框架式主体结构的中心部位安装由陀螺、加速度计等核心传感器件组合而成的惯性台体，在外围设置插槽安装各类功能运算电路板，在框架结构的外部通过一组减振器将整个惯导系统安装在导弹等载体上。由于陀螺、加速度计的性能对力学环境比较敏感，电路板上的力学环境对系统可靠性影响较大，均属于捷联惯导系统结构动力学设计与仿真分析的关注对象，一般需要对其结构进行详细建模。建模和计算工作均在经典ANSYS软件环境下完成。其中，主体框架结构、陀螺结构、加速度计结构、电路板结构均采用四面体高阶结构单元SOLID187来划分网格；惯导系统内外部声学环境采用四面体高阶流体单元FLUID221来划分网格，网格最大边长不超过5mm，满足在10000Hz（噪声场的最高频率）空气声波的一个波长上至少有6个网格的声学有限元建模准则。在流体网格与结构网格的交界上利用FSI界面载荷将结构运动与流体压力耦合在一起。系统减振器采用二节点弹簧阻尼单元COMBIN14来模拟，单元的一个节点与惯导系统主体框架有限元模型之间利用刚性约束单元固连在一起，另一个节点与大地固连，来自载体的随机振动载荷就施加在该节点上。惯导系统外部的声学载荷施加在框架结构的外露表面。有限元模型的三个坐标轴分别平行于六面体框架的三对外表面，为后面叙述方便，不妨定义X轴垂直于本文计算所关注的一块电路板的板面。计算所建立的捷联惯导系统声振耦合动力学有限元模型共有469533个结构单元，194152个声学单元，673160个节点。计算在一台内存64G、双CPU四核并行处理的小型工作站上完成。

捷联惯导系统的随机振动条件和噪声激励条件分别根据《GJB150.16A-2009军用装备实验室环境试验方法振动试验》与《GJB150.17A-2009军用装备实验室环境试验方法噪声试验》来确定。对于高超声速飞行器用捷联惯导系统，规范的随机振动条件和噪声激励条件分别见表1、表2。本文计算采用该条件，并假定随机振动条件与噪声环境条件互不相关。

表1 随机振动条件Tab.1 Random vibration condition

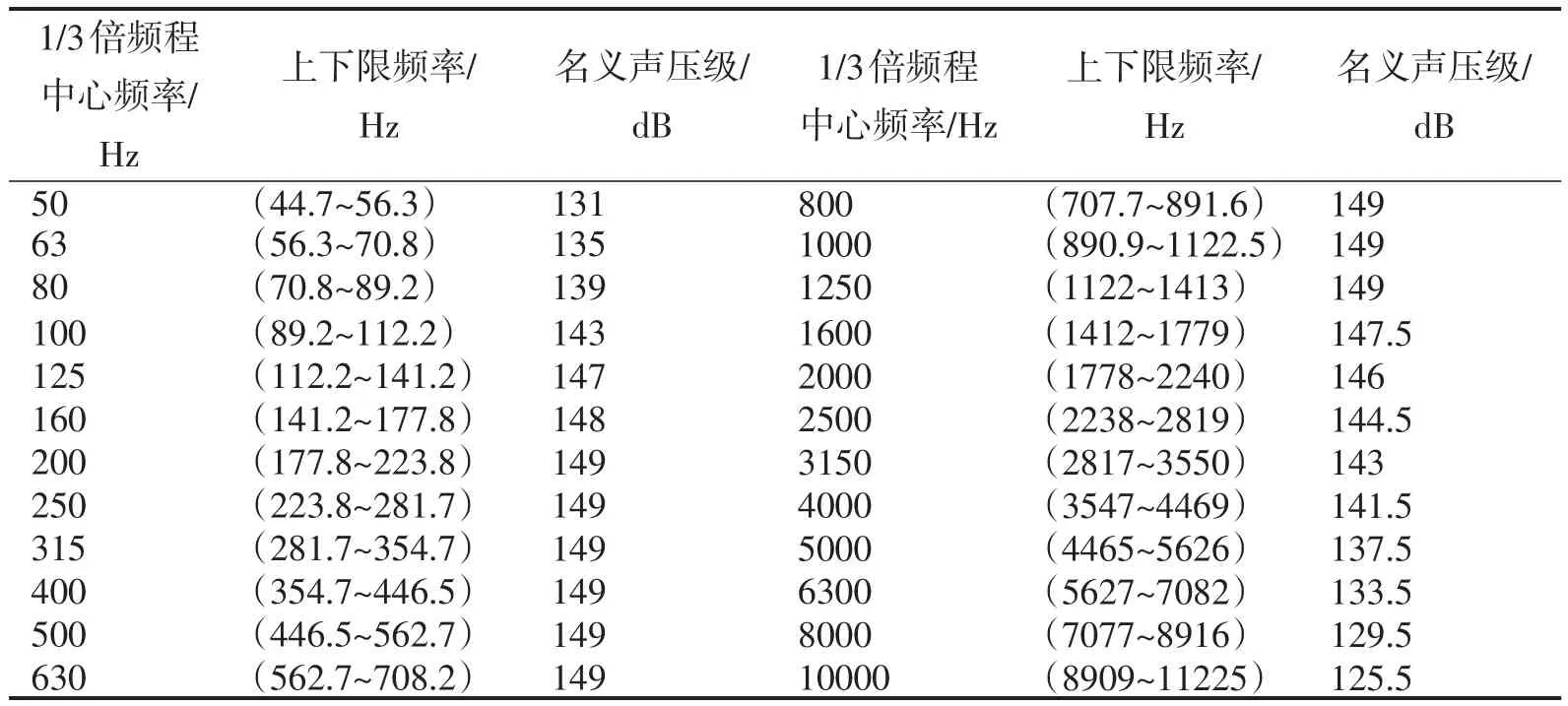
表2 噪声环境条件（总声压级为160dB）Tab.2 Acoustic environment condition(total spl 160dB)

3 计算结果与分析

首先分别计算了惯导系统结构有限元模型、惯导系统内部声学有限元模型以及惯导系统声振耦合有限元模型在10000Hz以下的固有模态，分析各频段的模态密度，以验证采用有限元方法进行计算的适宜性。然后对惯导系统声振耦合有限元模型进行单轴随机振动与噪声激励复合加载条件下的响应计算。选取两个测点来分析惯导系统的响应特性，一个测点选在陀螺的一个安装位置处，以评估惯性器件所承受的真实力学环境；另一个测点选在刚度最小电路板（注：其板面与X轴垂直）中央点处，以评估惯导系统内电路板的最大力学响应。为进行比较，还对惯导系统声振耦合模型在单独随机振动环境（单轴激励）、单独噪声场环境下的响应特性进行了仿真计算，测点位置保持不变。

表3所列是计算得到的惯导系统结构模态、声学模态及声结构耦合模态在不同频域的模态密度值。表中频段划分与表2声压谱的频程划分保持一致。从表3可以看出，无论是惯导系统结构模态密度还是声学模态密度均随着频率的升高而增加。但即使到8000Hz～10000Hz的高频段，惯导系统结构模态、声学模态及声—结构耦合模态的模态密度均甚小，远远低于适用统计能量法计算的模态密度要求。所以，捷联惯导系统的声振耦合问题适合用有限元法进行求解，不适合用统计能量法进行求解。

表3 惯导系统在不同频域的模态密度值列表Tab.3 Modal density of INS in different frequency range

图1、图2所示分别为惯导系统在综合环境条件（X轴向随机振动+噪声环境条件）激励下两测点处三个方向上的加速度功率谱密度响应曲线；图3、图4所示分别为惯导系统在X轴向随机振动激励下两测点处三个方向上的加速度功率谱密度响应曲线；图5、图6所示分别为惯导系统在噪声激励下两测点处三个方向上的加速度功率谱密度响应曲线。比较图上曲线的形状和量值，不难看出，图1逼近于图3和图5的叠加；图2逼近于图4和图6的叠加。即惯导系统在随机振动与噪声激励综合环境下的响应可以看成是在两种环境条件单独激励下的响应的叠加。所以，惯导系统在声振综合环境下的响应特性只是简单综合了在两种环境条件单独作用下的响应特性，二者的耦合效应可以忽略不计。因此，研究惯导系统在声振综合环境下的响应特性可以先分别研究在两种环境条件单独作用下的响应特性，然后再进行综合。

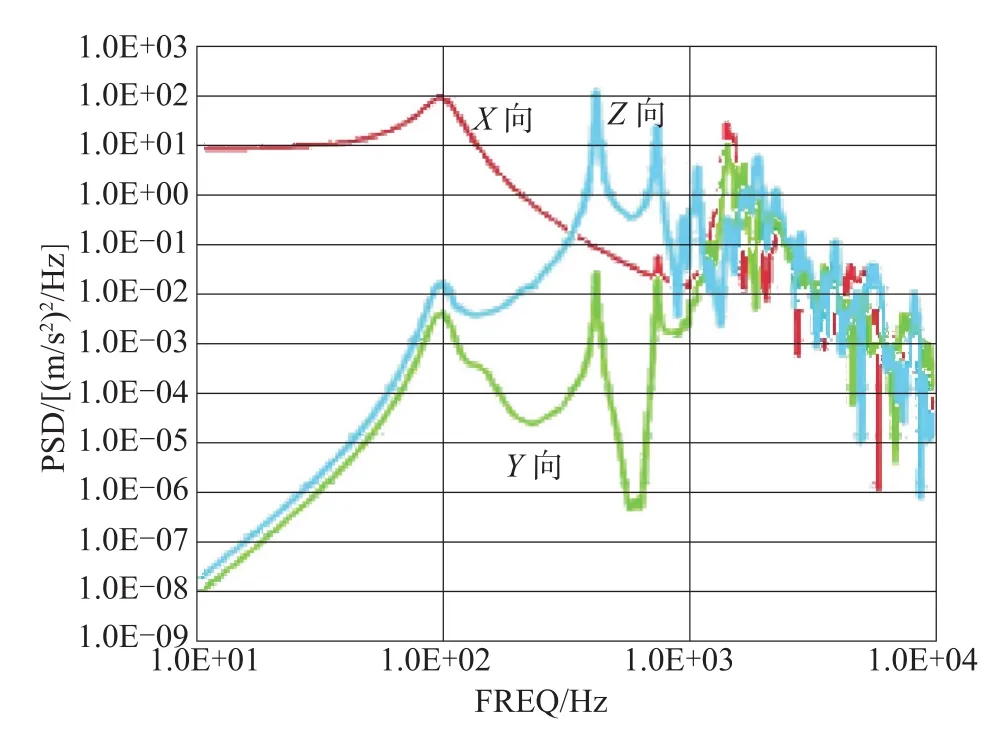
图1 综合环境条件下陀螺安装处三个方向上的加速度功率谱密度响应曲线Fig.1 Acceleration PSD curve of measuring Point1 in three directions under combined environment

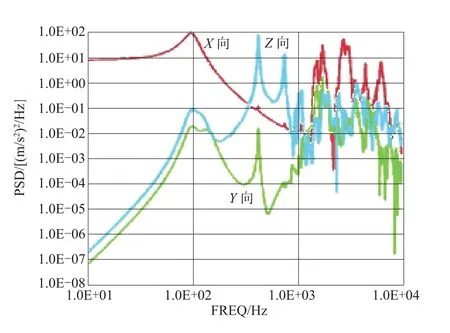
图2 综合环境条件下PCB中央点处三个方向上的加速度功率谱密度响应曲线Fig.2 Acceleration PSD curve of measuring Point2 in three directions under condition combined environment condition

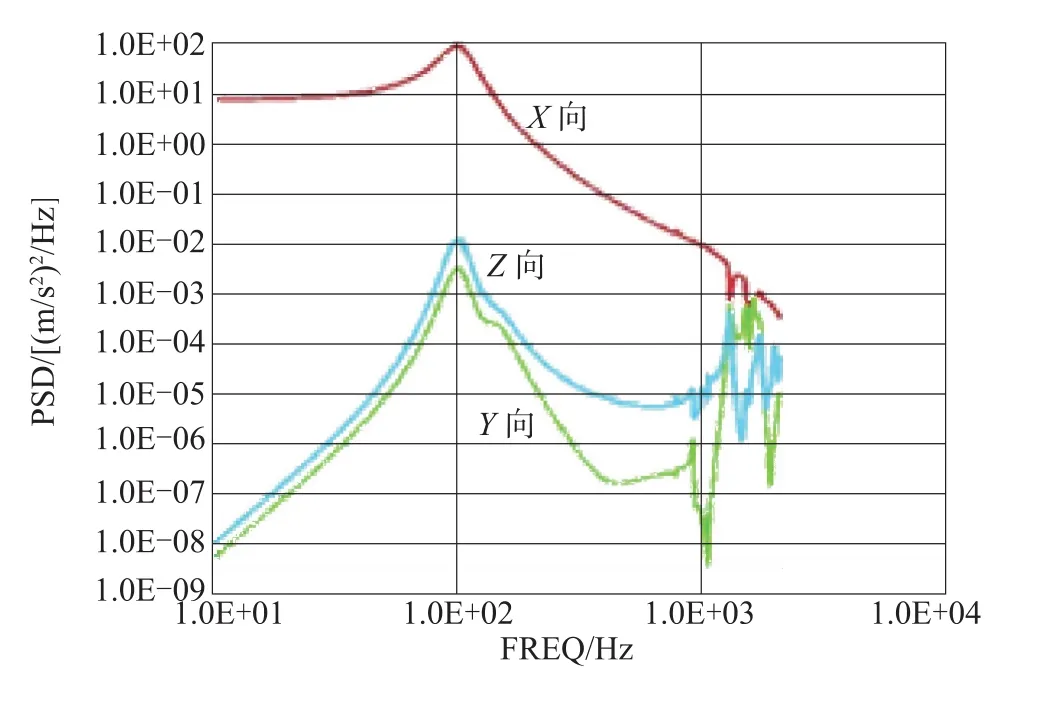
图3 随机振动激励下陀螺安装处三个方向上的加速度功率谱密度响应曲线Fig.3 Acceleration PSD curve of measuring Point 1in three directions under random vibration environment condition

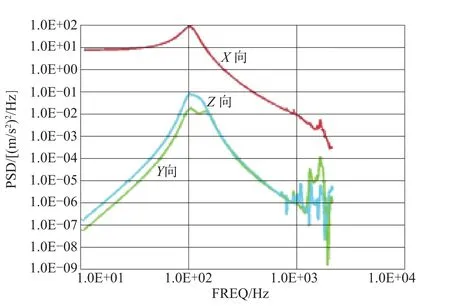
图4 随机振动激励下PCB中央点处三个方向上的加速度功率谱密度响应曲线Fig.4 Acceleration PSD curve of measuring Point 2 in three directions under random vibration environment condition

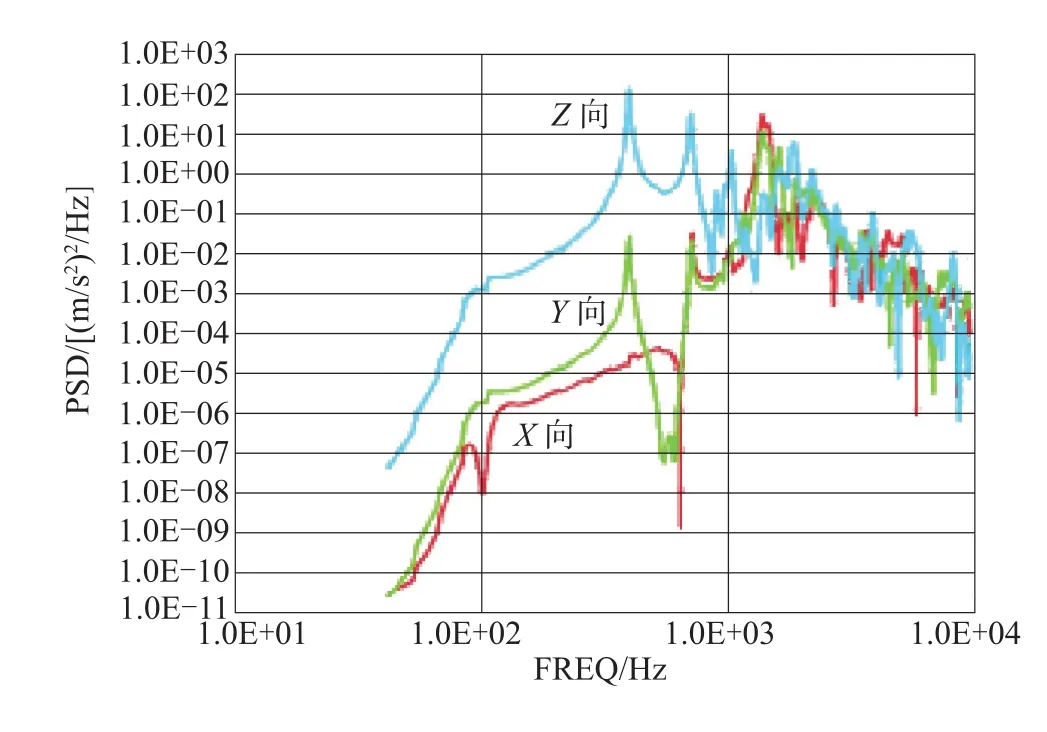
图5 环境噪声激励下陀螺安装处三个方向上的加速度功率谱密度响应曲线Fig.5 Acceleration PSD curve of measuring Point 1in three directions under acousti cenvironment condition

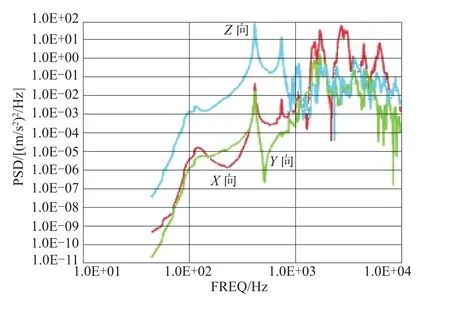
图6 环境噪声激励下PCB中央点处三个方向上的加速度功率谱密度响应曲线Fig.6 Acceleration PSD curve of measuring Point 2 in three directions under acoustic environment condition

为了更具体地分析响应的能量分布，对图1～图6各条曲线在频域上进行积分，分别列出它们在不同频段的加速度均方根值，如表4所示。

从图3、图4及表4可以看出，单轴随机振动主要是激起惯导系统在激振方向上的响应，非激振方向上的响应比激振方向上的响应要微弱得多。而且，由于减振器的作用，使得惯导系统的加速度响应主要集中在减振系统谐振频域以下的低频区域，高频区域的响应得到大幅衰减，无论是响应峰值还是响应能量都非常微弱。

从图5、图6及表4可以看出，环境噪声能够同时激起惯导系统在三个方向上的响应，且三个方向上的响应在同一量级，具体差别取决于结构的固有特性。本例中，惯性台体刚度均匀，三个方向上的响应量级差别不大。而PCB板三个方向刚度差别较大，所以板面法向上的响应要大于其它两个方向上的响应。与随机振动响应形成显著差别的是，惯导系统在200Hz以下的减振系统谐振区域几乎没有响应，其响应能量主要集中于惯导系统结构自身的谐振频率点附近。这说明，系统减振器对噪声激励没有衰减作用。对于刚度较好的惯性台体，其响应能量主要集中于2240Hz以下，在此频率以上则显著减小。这说明，环境噪声激起的主要是惯导系统主结构的少数几阶低阶模态。对于刚度较差的PCB板，环境噪声则能够激起较多阶板面法向振动模态，故其响应能量频域跨度较宽，但也主要集中在5000Hz以下频域。

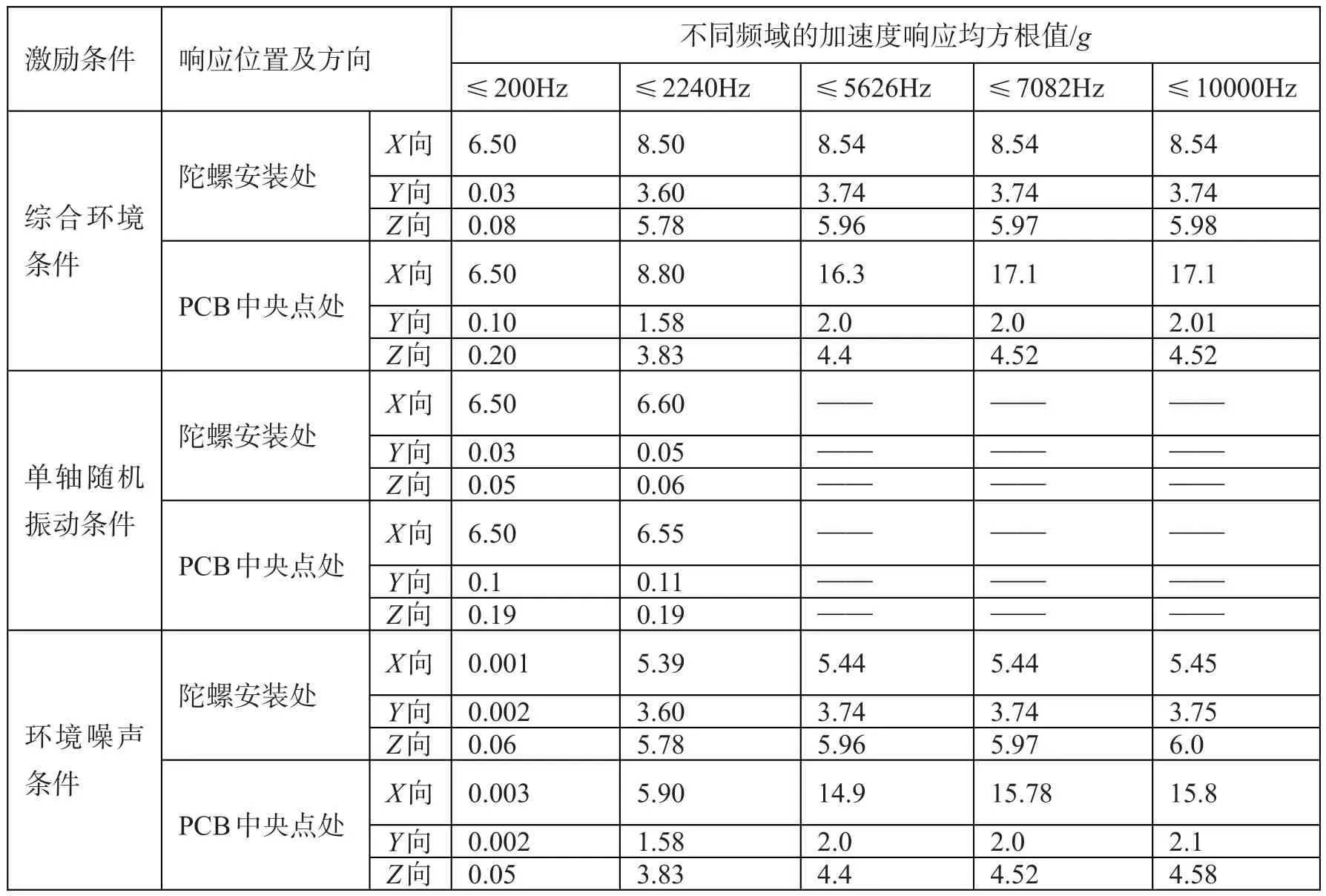
表4 不同频域的加速度响应均方根值Tab.4 Acceleration RMS in different frequency range

4 讨论与结论

航天系统及设备在综合环境作用下的全频域力学环境预示一直是航天综合环境试验技术与航天结构环境适应性设计技术的关键和难点。一般认为，在中低频段宜采用有限元法进行计算，在高频段宜采用统计能量法进行计算。但如何划分低频、中频、高频3个频段,仍然缺乏一个量化的界定标准。常见的做法是根据频率值来界定。这显然是不合适的。本文没有固守这种成见，提出根据模态密度选择计算方法，并详细论证了有限元法适用于对捷联惯导系统这类结构紧凑型弹上设备进行宽频域声振耦合仿真计算。计算结果显示，捷联惯导系统的结构模态密度和内声场模态密度都很低，远远不满足统计能量法的使用要求；结构上的加速度响应主要集中在2240Hz以下频域，最坏情况也不超过5000Hz。所以，即使5000Hz以上频域的计算存在一些误差，但对全频域的计算结果影响较小，在工程上是可以接受的。在此前提下，本文工作才得以展开。

在环境噪声激励下，捷联惯导系统结构呈现出三轴响应的特点。在本例中，尽管每一轴向上响应的加速度均方根值均比单轴随机振动条件下的略小，但三轴合成的结果（8.68g）要明显大于单轴随机振动响应。而且，捷联惯导系统结构在环境噪声激励下的响应主要集中在几百Hz到几千Hz的高频段，更加接近于或能够覆盖惯性器件结构的低阶固有频率，对惯性器件的影响远大于随机振动带来的200Hz以下的低频载荷。当前，惯性器件力学环境适应性试验研究主要采用单轴随机振动的加载方式，三轴加载是否会激发新的故障模式，尚待研究。所以，随着导弹等航天器飞行速度的提高，声振综合环境成为弹上电子设备通常需要面对的力学环境条件，将会给惯性器件的环境适应性研究带来诸多新课题。

最后，对捷联惯导系统结构在声振综合环境下的响应特性作简要总结：①在随机振动与噪声激励综合环境下的响应等效于在两种环境条件单独激励下的响应的叠加；②在三个轴向上均有明显的响应，且量级相当，这与在单轴随机振动条件下主要是激振方向上响应的情况显著不同；③在随机振动激振方向上的响应是随机振动与噪声激励共同作用的结果，二者的作用均不容忽视；④在非振动激振方向上的响应则主要表现为对噪声激励的响应，随机振动的作用要微弱得多；⑤惯性台体的加速度响应能量主要集中于2240Hz以下的频域内，刚度相对薄弱的结构（如PCB板等）的加速度响应能量的频域跨度较宽，但主要集中在5000Hz以下频域；⑥在惯性台体上响应的加速度均方根值相等的情况下，综合环境条件对惯性器件的影响比单轴随机振动条件的影响更大。

[1]宋文治.NASA在声振领域研究的新成果[J].强度与环境,2006,33(2):58-64.

[2]王珺，张景绘，宁玮.复合环境激励下的声振耦合分析[J].振动与冲击，2011,30(2):15-18.

[3]张正平,王宇宏,朱曦全.动力学综合环境试验技术现状和发展[J].装备环境工程,2006,3(4):7-11.

[4]邹元杰，韩增尧，张瑾.航天器全频域力学环境预示技术研究进展[J].力学进展,2012,42(4):445-451.

[5]姚德源,王其政.统计能量分析原理及其应用[M].北京:北京理工大学出版社,1995.

[6]GJB 150,军用设备环境试验方法[S].2009.

[7]ANSYS Theory Reference[R].Ansys company,2012.

[8]DesmetW,TournourM.LMS International Numerical Acoustics Theoretical Manual[M].2000.

Study on Dynamic Response of SINS to Vibro-acoustic Combined Environment

YAO Jian-jun，YU Sheng-qiang，ZHEN Rui，YAN Hong-song，YIN Zeng-zhen，LIU Zhi-jun
(Beijing Institute ofAutomatic Control Equipment,Beijing 100074,China)

Along with the enhancement of spacecraft’s flight velocity,acoustic environment can not be neglected,and vibro-acoustic combined environment is the mechanics environment condition that SINS and other missile-borne electronic equipments often suffer.It is argued that in this paper,FEM method can be applied to simulate vibro-acoustic coupled problems of SINS and other compact structure equipments in a wider frequency range.The dynamic response of SINS to vibro-acoustic combined environment is simulated,and contrasted with the response to random vibration environment and the response to acoustic environment.Then its characteristics are educed.The conclusions are helpful to design or evaluate land dynamic experimentation,and predict or analyse environmental worthiness of SINS under vibro-acoustic combined environment.

Strap-down Inertial Navigation System（SINS）；Combined environment；Vibro-acoustic coupling；Dynamic response

V414.1

A

2095-8110（2015）02-0073-08

2014-10-29；

2014-11-30。

姚建军(1974-)，男，研究员，主要从事多物理场仿真分析与结构功能一体化设计方面的研究。E-mail:yjjnl@sina.com