基于支持向量机集成学习方法的高新技术上市公司绩效预测研究
2015-04-17吴荣顺王丹阳戚啸艳
吴荣顺 ,王丹阳,戚啸艳,
(1东南大学 反腐败法治研究中心,江苏 南京 210096;2东南大学 经济管理学院,江苏 南京 210096)
一、引 言
近年来,我国高新技术企业发展势头强劲,相当多的企业进入了资本市场。然而,随着竞争的全球化以及技术升级周期的短期化,高新技术企业发展的不确定性显现,股东、债权人等外部利益相关者需要更有效的绩效预测方法,为其决策提供依据,实现既定风险下的收益最大化。
支持向量机模型(Support Vector Machine,简称SVM)最早由Vapnik提出,是典型的人工智能算法预测模型之一。支持向量机模型因其在解决小样本、非线性以及高维识别模式中表现的各种优势而被应用于预测领域,如Fan等人[1]采用多种模型预测企业绩效,实证结果显示SVM模型预测准确度高于多元判别模型和神经网络模型。Shin[2]选取1996年到1999年韩国破产企业作为研究对象,分别构建神经网络模型和SVM模型对样本企业进行绩效预测,结果显示SVM模型预测总体表现优于BP神经网络模型,并且训练样本越小,这种优异性越明显。张再旭等人[3]引入支持向量机构建企业绩效预测模型,结果表明该模型具有较高的预测精确度。张晓琦[4]以企业是否爆发大规模财务危机从而发生银行贷款违约且违约时间在一年及以上作为分类标准,选取浦东发展银行全国客户池中75家未上市高新技术企业作为研究样本,其中包含50家财务正常企业和25家违约企业,构建SVM模型,实证结果显示SVM模型预测效果较为理想。
为了进一步改进支持向量机的预测准确度,本文试图将集成学习方法引入支持向量机预测模型,并将其应用于高新技术企业的绩效预测。
二、支持向量机集成学习方法的基本原理及模型
1.支持向量机学习方法基本原理
支持向量机是在统计学习理论的基础上发展起来的一种新的学习方法,它基于结构风险最小化原则,能有效地解决学习问题,具有良好的推广性和比较好的分类精度。
使用Adaboost构建支持向量机集成学习方法时,先将支持向量机方法定义为弱分类器,支持向量机集成学习方法定义为强学习器,所构建的支持向量机集成学习方法是将原始数据的分类过程等分为若干层支持向量机弱学习器的组合叠加,每层抽选固定数量的样本,使用支持向量机弱分类器进行分类处理,对于每层处理结果中分类正确和错误的样本分别减少和增加其权重,使得支持向量机弱分类器聚焦在那些分类困难的数据样本上,最后使用权重投票方式对支持向量机弱分类器进行融合,得到最终的支持向量机集成学习方法强分类器[5]。
2.支持向量机与支持向量机集成学习方法模型的构建
(1)支持向量机模型构建
支持向量机模型的构建主要有以下几步:第一步是对数据集的整理,通过查询数据库取得建模需要的数据指标,剔除数据缺失样本。将初步得到的数据样本通过SPSS软件进行非参数检验以及T检验、相关性检验之后得到指标体系,再将其按照libsvm要求的格式进行整理,得到最终的建模数据集;第二步是将数据集进行归一化处理,将其规范到[0,1] 范围内;第三步是核函数的选择,由于径向基核函数(RBF核函数)的应用范围相对较广,不论低维度还是高维度,大样本还是小样本都适用,因此本文选择径向基核函数(RBF核函数)作为构建高新技术企业绩效预测模型的核函数;第四步是参数的设置,选择是RBF核函数涉及参数g和惩罚因子c,本文使用网格搜索法确定参数g和c;最后一步是对训练集进行训练获取模型并进行预测,首先将样本企业人工分为训练集和测试集,将训练集通过训练得到预测模型,然后用测试集检测模型精度。
(2)支持向量机集成学习方法预测模型的构建
在构建支持向量机集成学习方法预测模型时,为了使得所构建的支持向量机集成学习方法预测模型与单一支持向量机模型具有可比性,样本选取与最优参数和构建单一支持向量机预测模型时相同。构建支持向量机集成学习方法预测模型的步骤如下:
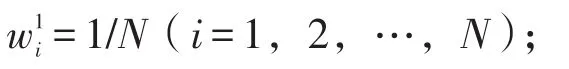
步骤二,for t=1to T do;
步骤四,根据抽样得到的m个样本集构造弱分类器,即子支持向量机分类器gt;
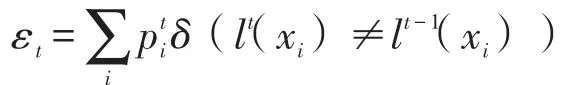
步骤六,如果εt>0.5,则重置wi=1/N(i=1,2,…,N),返回步骤三;
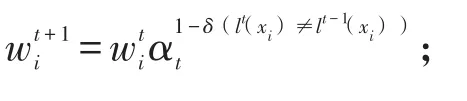
步骤八,end for
三、高新技术上市公司绩效预测指标体系
企业经营的最终目标是创造价值,因此企业绩效预测可以理解为企业价值预测[6]。汤谷良等人[7]认为企业价值由增长、盈利和风险三个维度构成,成长是企业在运营过程中业务的增长程度和速度,盈利是企业获得超额收益的能力,风险是企业在运营过程中存在的财务风险和经营风险,只有完成对企业增长、盈利、风险的三重管理任务,企业价值目标才能得到保证。钱爱民和张新民[8]在此基础上建立企业财务状况质量三维综合评价体系,并将其应用于对我国A股制造业上市公司绩效的检验。因此,本文将采纳汤谷良等人的观点,以创业板高新技术企业为样本,从盈利、成长和风险三维度评价企业绩效。
(1)成长性指标。企业成长需要从成长速度以及运营过程中经营资产质量两个方面考察,成长速度可以通过企业资产增长率进行反映,经营资产质量可以通过企业资产周转性进行反映。
(2)盈利性指标。企业盈利性需要从盈利数量和盈利质量两个方面考察。盈利数量是企业的盈利水平,可通过企业财务报表直接获得;盈利质量则是隐形的,是企业盈利水平的内在表现,需要结合企业利润与现金流量相关指标进行分析。
(3)风险性指标。企业发展面临诸多风险,创业板高新技术企业处于高速成长期,需要大量资金支持,财务风险是其主要风险之一。考虑到数据的可得性,关于风险维度,本文仅考察企业的财务风险,用流动负债占比考察企业债务的期限构成;用流动比率、速动比率、现金比率考察资产对负债的保障程度;用利息保障倍数、现金流动负债比率、现金流利息保障倍数、现金债务总额比等来考察现金对负债的保障程度;此外,衡量企业财务风险还需要考察企业的长期还款能力,考察指标主要有资产负债比率、产权比率、长期资本负债比率等。归纳分析后,得到表1。
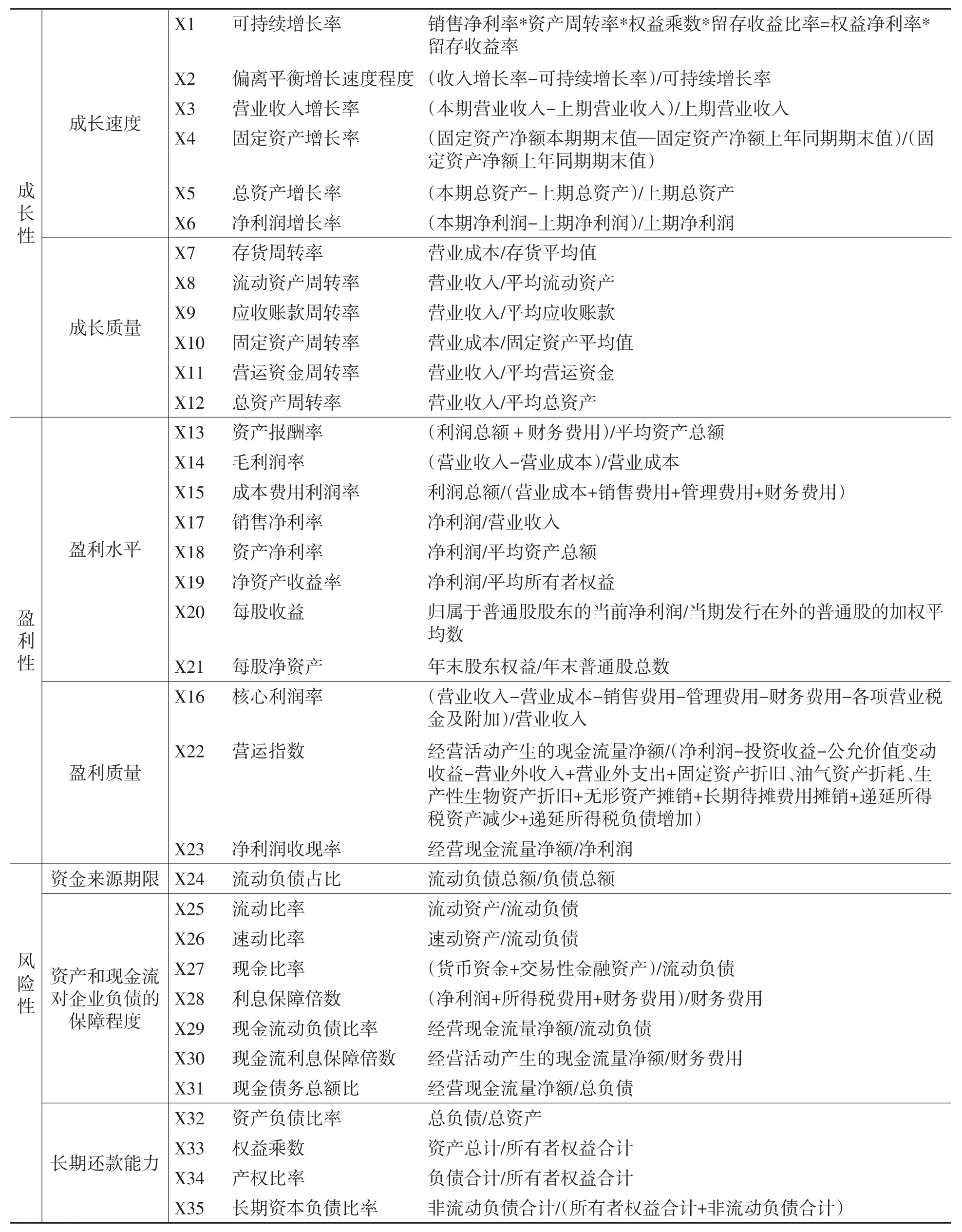
表1 指标的初步选取
表1指标只是从理论上进行选择,构建基于支持向量机集成学习方法的高新技术企业绩效预测模型,需对指标进行进一步的处理,如指标的标准化、正态分布检验、非参数检验、T检验以及相关性检验等。
四、实证结果与分析
基于支持向量机集成学习方法的企业绩效预测主要包括三大步骤:一是样本企业选取与判别分类;二是变量筛选过程,包括建模指标选取以及通过统计软件进行指标筛选;三是支持向量机及支持向量机集成学习方法模型的构建,包括选定测试集和训练集,建立子分类器,测试数据验证以及子支持向量机的集成。
1.样本的选取与数据来源
我国创业板成立时间较晚,国泰安数据库的统计数据显示,2013、2012、2011和2010年能查到公司数据的企业分别为379、355、293和181家。本文将2013年作为预测年度,设为t年,2012年为t-1年,以此类推,对2013年进行预测,需要2012、2011、2010年的数据。剔除非高新技术企业,并通过查阅企业对应年度财务报告补全数据库中缺少数据,最终得到用于t-1年预测的企业共有273家,用于t-2年预测的企业共有172家。
2.样本企业绩效状况的判别与分类
学界通常将上市公司是否被ST作为判别企业绩效好坏的标准,由于创业板成立时间较短,目前尚无ST公司。因此,本文结合创业板上市的高新技术企业的特点及实际情况,找出合理的分类和判定标准,以得到适宜的样本。
根据《深圳证券交易所创业板股票上市规则》(2012年修订)中第十三章暂停、恢复、终止上市的描述,判定这些企业财务状况好坏的标准可通过重点关注企业的净利润、净资产及年度会计报表审计意见。将符合下述条件的企业的、判别为绩效状况劣:(1)t年净资产为负;(2)t年与t-1年净利润为负;(3)t年相对于t-1年利润大幅下滑超过50%;(4)最近两个年度会计报表被注册会计师出具否定意见或保留意见。
经过分析,t-1年模型预测中,样本企业共有273家,其中,财务正常的企业有230家,财务非正常企业有43家。t-2年模型预测中,样本企业共有172家,其中,财务正常的企业有143家,财务非正常企业有29家。用表格表示如表2。

表2 高新技术企业绩效判定结果
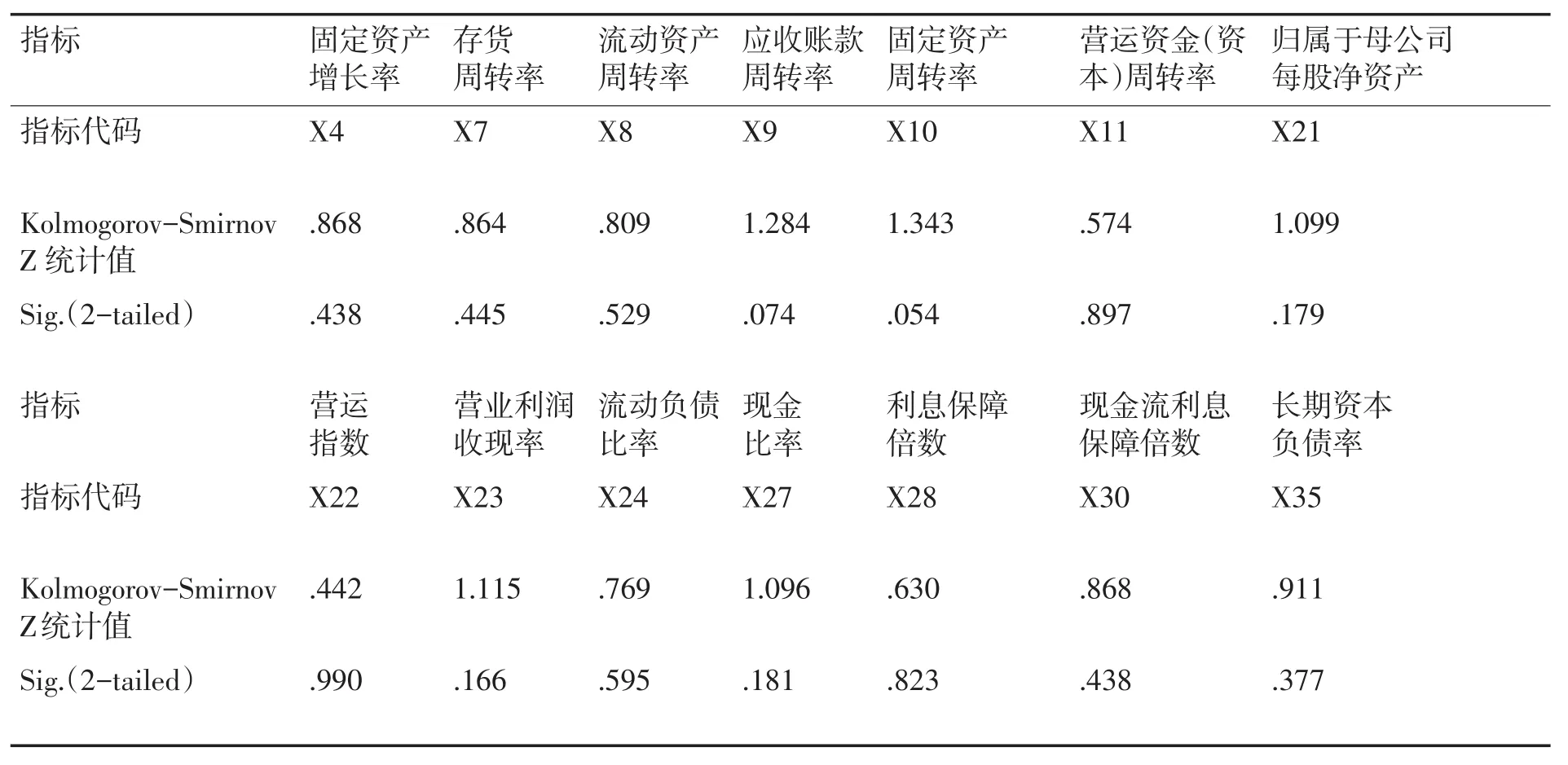
表3 K-S检验结果
3.绩效预测指标的筛选
考虑到指标量纲的差异可能会对结果产生影响,因此首先对原始数据进行标准化处理。
本文选取了35个指标,数量较多,在构建支持向量机预测模型之前需要对其进行初步分析,筛选出能够鉴别高新技术企业不同财务状况的指标。
首先对选取的指标进行非参数检验中的Kolmogorov-Smirnov检验,得到结果表3。
K-S检验结果显示14个指标符合正态分布,可以使用参数检验中的独立样本T检验,判断这些指标在不同主体中是否存在显著性差异,处理结果如表4。
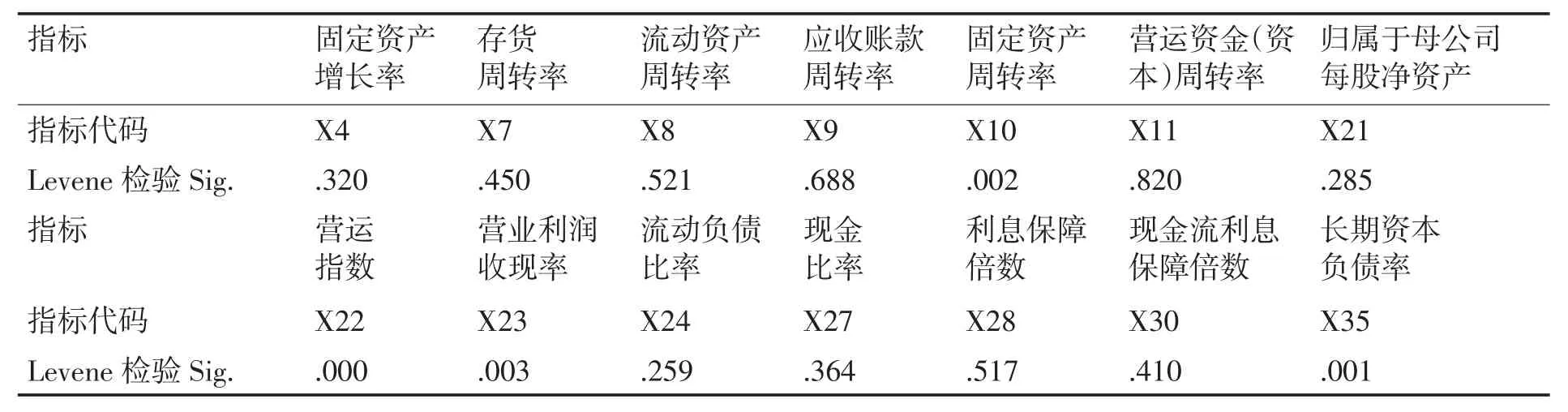
表4 独立样本检验
从上述结果中可以看到,X4、X7、X8、X9、X11、X21、X24、X27、X28、X30的方差方程的Levene检验的显著性大于0.05,这些指标具有显著性差异,因此应该保留;而X10、X22、X23、X35这四个指标Levene检验的显著性小于0.05,不具有显著性差异,不能有效构建高新技术上市公司绩效预测模型,因此应该剔除。
对于除上述未经过独立样本T检验的不服从正态分布的指标,由于不满足独立样本T检验的条件,因此需要将其进行非参数检验,选用两独立样本的非参数检验。本文选用曼—惠特尼U检验,结果如表5。
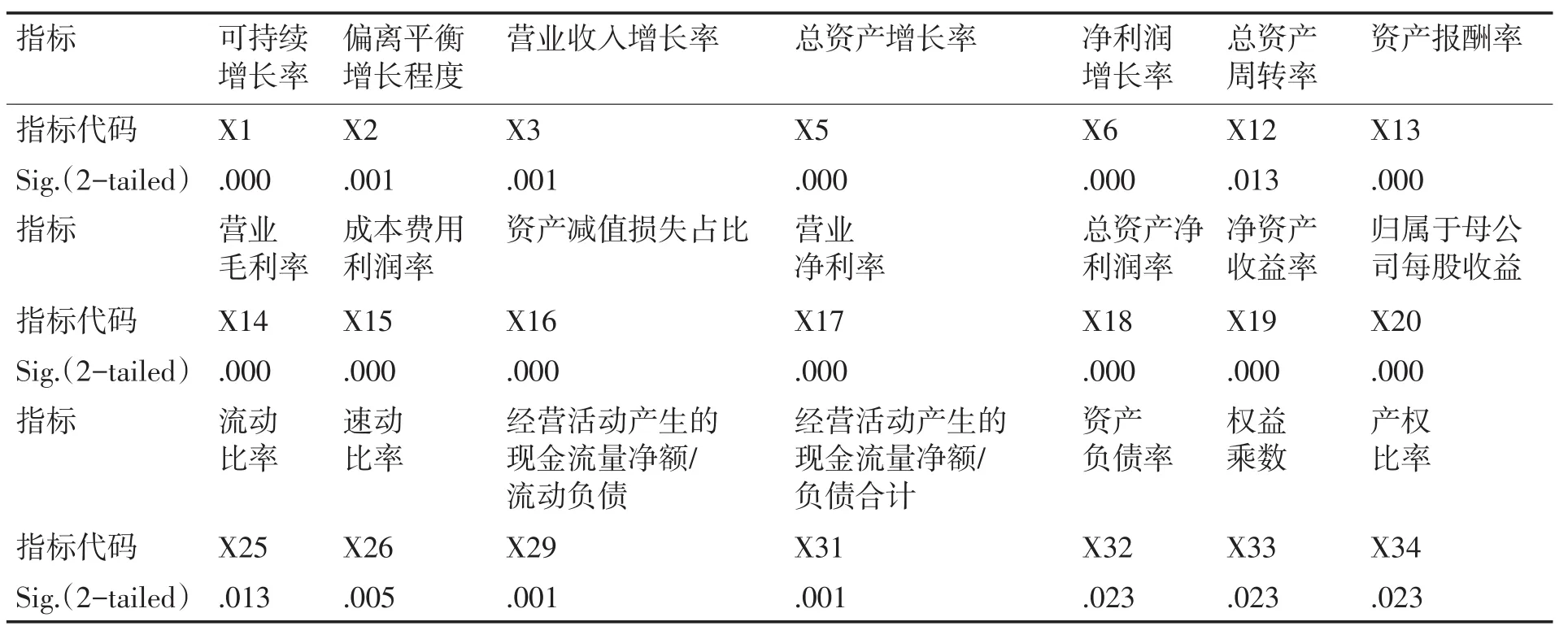
表5 非参数检验结果
由上述结果可知,上述15个指标显著性性均小于0.05,具有显著性,应该保留这些指标。
经过上述步骤,剔除与保留下来的指标汇总如表6。

表6 样本指标选取结果
对经过上述步骤保留下来的指标进行相关性分析。本文选用Pearson简单相关系数检验,通过比较相关系数进行指标的筛选。将≥0.6的两变量之间认为存在较强的相关性。X1、X13、X17、X18、X19、X20指标之间具有较强的相关性,将X1作为代表指标,剔除其余指标;X25、X26、X27、X29这四个指标相关性较强,选取X25作为代表指标;X32、X33、X34这三个指标相关性较强,选取X33作为代表指标;X8、X12这两个指标相关性较强,选取X8作为代表指;X14、X15这两个指标相关性较强,选取X14作为代表指标。结果见表7。

表7 指标选取最终结果
4.预测模型的测试
构建企业绩效预测模型,需要注意两方面的结果,一是预测结果的正确率,二是预测结果的误判率。预测结果的误判率对于预测结果有着非常重要的意义。误判率分为两种形式,一种称为“型一错误”,即“弃真错误”,第二种称为“型二错误”,即“纳伪错误”。本文将“型一错误”定义为绩效不正常企业误判为绩效正常企业,将“型二错误”定义为绩效正常企业误判为绩效不正常企业。
根据以上说明,本文将列出如下公式:
型一错误率=非正常企业判为正常企业样本数量/测试集样本中非正常企业数量
非正常企业样本预测准确度=1-型一错误率
型二错误率=正常企业判为非正常企业样本数量/测试集样本中正常企业数量
正常企业样本预测准确度=1-型二错误率
总体预测准确度=测试集中被正确分类的样本数/测试集样本企业数量
(1)支持向量机模型测试
构建支持向量机预测模型时,分为t-1年预测和t-2年预测
①t-1年测试
t-1年模型预测中,样本企业共有273家,其中,财务正常的企业有230家,财务非正常企业有43家。预测指标为经过筛选的指标,共19个。支持向量机模型的构建在Matlab中实现,同时使用台湾大学林智仁教授开发的libsvm 3.17软件包。首先进行数据集的整理,将样本指标归一化到[0,1] 区间范围内,选择构建模型选择RBF核函数,并在MATLAB中确定惩罚参数c和核函数参数g,采用网格搜索法进行K折交叉验证找出最佳参数。经过检验,当K为6时,支持向量机的性能最好,CV准确度为95.22%,此时模型参数c和g分别为1024和0.25。我们将构建6个支持向量机预测模型。将样本数据的6部分分别用A、B、C、D、E、F表示,由SVM_Adaboost运算原理可知,在构建支持向量机模型时将其中5组作为训练集,另一组作为测试集,使得样本中每一部分都有机会被抽中,由此构建出6个子支持向量机模型,得到的预测结果也是6组,分别用A-B-C-D-E、A-B-C-D-F、A-B-C-E-F、A-B-D-E-F、A-C-D-E-F、B-C-D-E-F表示。
通过将样本企业指标数据导入MATLAB软件中,并使用libsvm工具箱构建预测模型,得到的预测结果如表8所示。
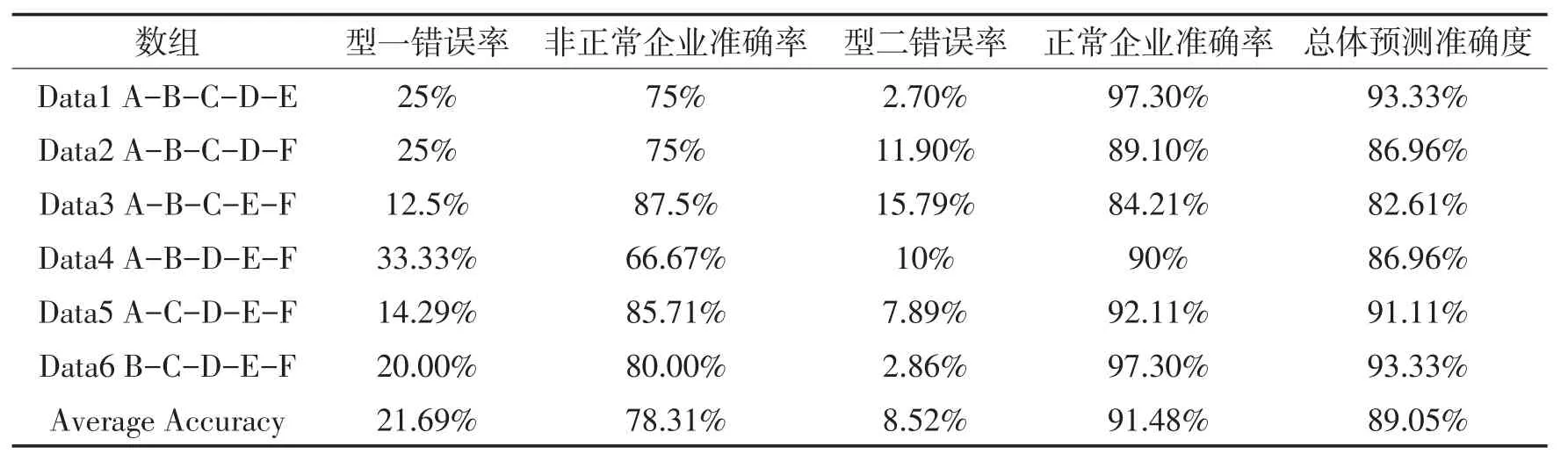
表8 t-1年支持向量机模型预测结果
从上述表格的预测结果中可以看出,构建的6个支持向量机模型最终得到的总的预测精确度为89.05%。其中,出现的型一错误率为21.69%,出现的型二错误率为8.52%。可以看出,在预测时,构建的支持向量机学习方法绩效预测模型的型一错误率较高,达到21.69%,高于型二错误率8.52%。根据上文中对预测结果准确度指标的解释可知,当型一错误率高于型二错误率时,说明所构建模型对企业未来绩效预测效果不够理想,预测结果的失真可能会对股东、债权人等外部相关者的投资决策提供误导从而导致可能带来的投资失误带来的巨大损失。因此需要对模型进行改进,提高其适用能力。
②t-2年测试
测试步骤同t-1年,采用网格搜索法进行K折交叉验证找出最佳参数,最终得到K值取4,佳参数c和g分别为0.25和0.0156,我们将构建4个弱分类器,即4个支持向量机预测模型。得到的预测结果也是4组,分别用A-B-C、A-B-D、A-C-D、B-C-D表示。同t-1年预测相同,预测得到的指标值有四种。将样本以及运算获得的参数输入MATLAB中构建模型,得到的预测结果如表9。
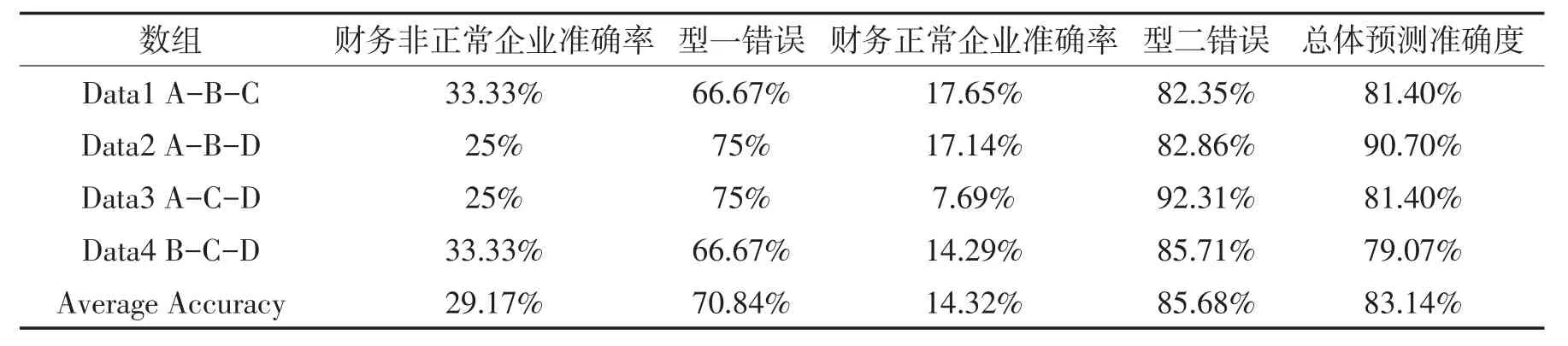
表9 t-2年支持向量机模型预测结果
从上述表格的预测结果中可以看出,构建的4个支持向量机模型最终得到的平均预测精确度为83.14%,预测精确度较高。其中,出现的型一错误率为29.17%,出现的型二错误率为14.32%。同样,在构建的t-2年支持向量机预测模型中,虽然总体预测准确度较高,达到83.14%,但是,该模型型一错误率为30.21%,高于型二错误率14.2%,说明将非正常企业判定为正常企业的概率大于将正常企业判定为非正常企业的概率,会给相关投资者投资决策提供错误指导的风险较大,因此需要对该模型进行改进。
(2)支持向量机集成学习方法模型测试
对支持向量机集成学习方法预测模型测试结果同样用5个指标表示。
①t-1年测试结果
将样本数据代入MATLAB并使用libsvm工具包进行运算得到结果如表10。
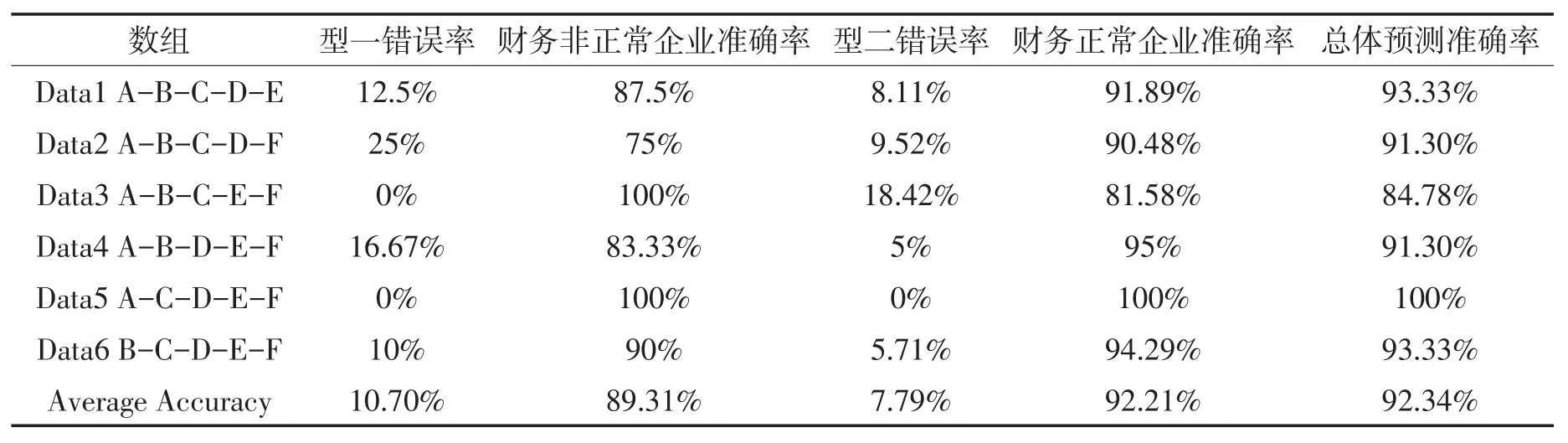
表10 t-1年支持向量机集成学习方法模型预测结果
从上述表格的预测结果中可以看出,分别用不同的数据组构建出6个支持向量机集成学习方法模型并用不同测试集进行测试得到的预测准确度的平均值为92.34%,预测精确度相对支持向量机预测模型精确度更高。其中,出现的型一错误率为10.70%,仍然高于出现的型二错误率为7.79%,即将非正常企业判为正常企业的概率高于将正常企业判为非正常企业的概率。在支持向量机绩效预测模型的测试结果分析中已经说明,若预测结果中出现的型一错误率高于出现的型二错误率,说明所构建的模型可能会给股东、债权人等外部利益相关者的投资决策提供错误指导,从而可能造成这些投资者的较大的损失。然而通过分析6组数组的预测结果可以看出,虽然最终得到的型一错误率平均数值高于型二错误率,但相对于上节中支持向量机预测模型的预测结果型一错误率有了较大的下降。因此,本文所构建的支持向量机集成方法预测模型是有意义的,能够帮助利益相关者们的决策提供相关的决策支持。
此外,由于原始样本中正常企业与非正常企业的数量不均衡,非正常企业样本数量相对于正常企业样本数量较小,也会对最终预测准确度的计算造成干扰,如何克服这种干扰,本文作者将在后续研究中进行探究。
②t-2年预测结果
将样本数据代入MATLAB并使用libsvm工具包进行运算得到结果如表11。
从表11的预测结果中可以看出,构建的4个子支持向量机模型经过Adaboost集成之后最终得到的总的预测精确度为84.72%,预测精确度相对支持向量机模型精确度更高。其中,出现的型一错误为21.18%,出现的型二错误为14.97%。
(3)两种模型预测结果对比分析
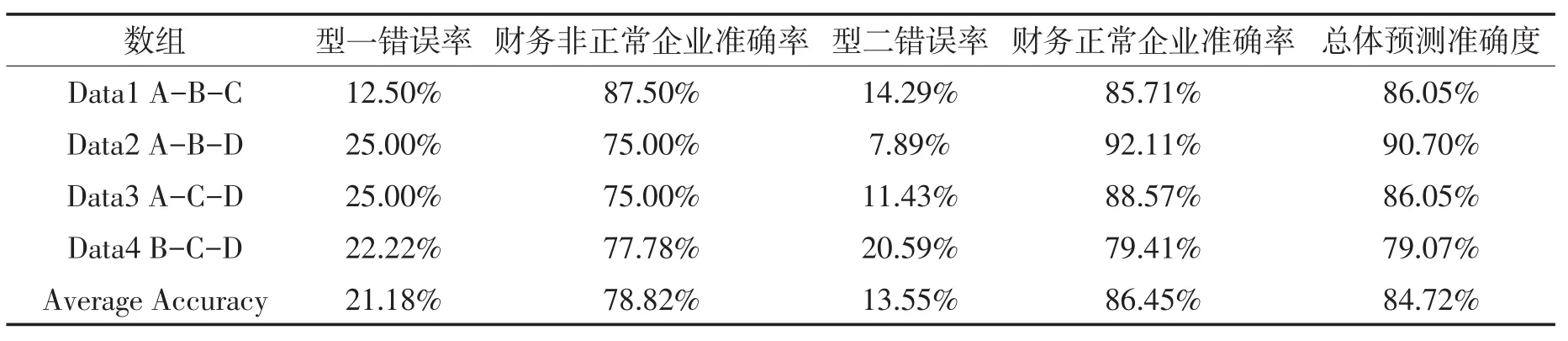
表11 t-2年支持向量机集成学习方法模型预测结果
将构建的t-1年t-2年的两类模型的预测结果进行分析,得到表12。
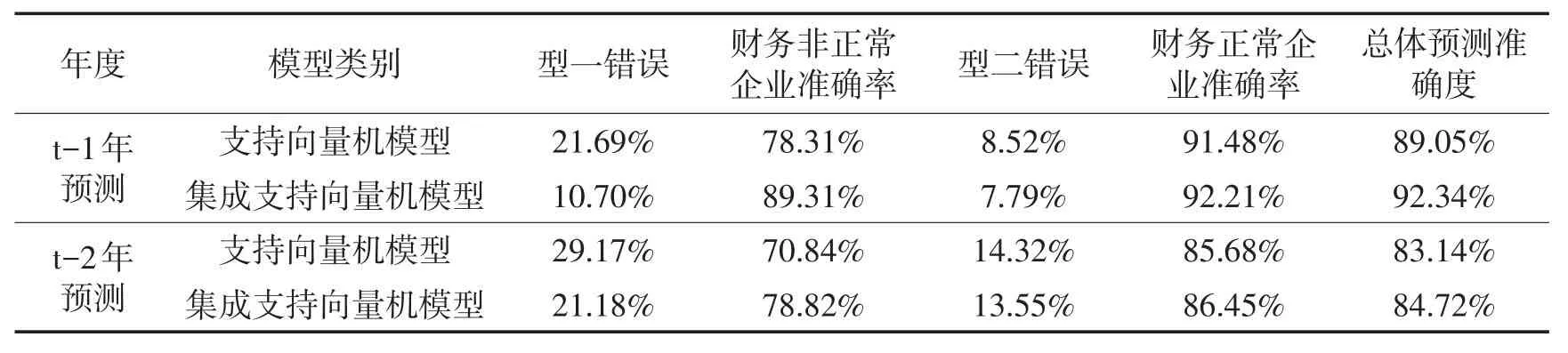
表12 两种模型预测结果比较分析
t-1年预测结果显示,支持向量机集成学习方法预测模型的预测精度92.34%高于支持向量机预测模型的预测精度89.05%,即支持向量机集成学习方法构建的预测模型预测精度高于支持向量机构建的模型;型一错误率,也即为将财务非正常企业误判为财务正常企业的错误率有了明显降低,支持向量机的型一错误率为21.69%,而支持向量机集成学习方法的型一错误率为10.70%;型二错误也即为将财务正常企业误判为财务正常企业的错误率也降低,支持向量机型二错误率为8.52%,而支持向量机集成学习方法预测模型的型二错误率为7.79%,低于支持向量机预测模型。由此可得出支持向量机集成学习方法模型的预测效果整体高于支持向量机预测模型的预测效果,使用支持向量机集成学习方法预测模型能够为高新技术企业的股东、债权人等利益相关者提供更为准确的决策支持。
t-2年预测结果显示,支持向量机集成学习方法预测模型的平均预测精度84.72%,高于支持向量机预测模型的预测精度83.14%,即支持向量机集成学习方法构建的预测模型预测精度高于支持向量机构建的模型;支持向量机的型一错误率为29.17%,而支持向量机集成学习方法模型的型一错误率为21.18%;支持向量机型二错误率为14.32%,高于支持向量机集成学习方法预测模型的型二错误率为13.55%。由此可知在t-2年预测中,支持向量机集成学习方法模型的预测效果整体高于支持向量机预测模型的预测效果,使用支持向量机集成学习方法预测模型能够为高新技术企业的股东、债权人等利益相关者提供更为准确的决策支持。
t-1年预测结果与t-2年预测结果进行对比,不管是支持向量机预测模型还是支持向量机集成学习方法预测模型,其t-1年预测结果型一错误率、型二错误率,均低于t-2年预测结果。由此可知,越接近预测年度,构建出的模型预测效果越好。对于高新技术企业的股东、债权人等利益相关者而言,构建的模型的预测应尽量参照接近预测年度的数据构建的预测结果,以减少决策失误的风险。
由上述对比结果可知,使用支持向量机集成学习方法构建的t-1年预测模型的预测精确度最高,平均预测准确度可达到92.34%,可使用t-1年支持向量机集成学习方法预测模型对未来一年绩效进行预测。
5.模型预测的应用
由测试结果可知,运用支持向量机集成学习方法构建的t-1年预测模型的预测准确度较高,达92.34%。现随机抽取10家样本企业,将这些企业2013年的数据指标代入已构建的t-1年支持向量机集成学习方法预测模型预测2014年的绩效情况,并将其与实际绩效状况进行比较,以验证所构建模型的有效性,得到的结果如表13。
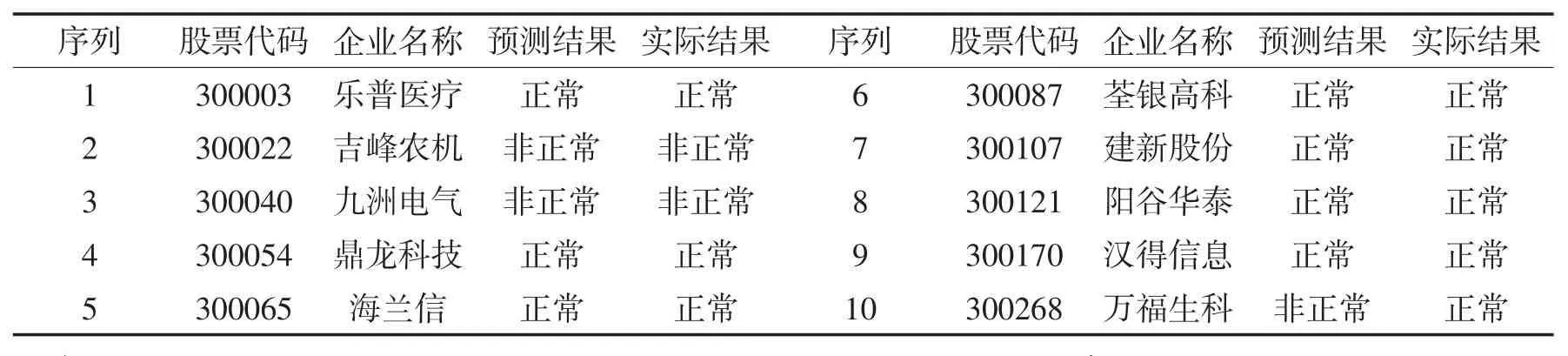
表13 预测结果
由表13的预测结果可知,随机抽取的10家企业中,绩效正常企业有7家,绩效非正常企业有3家,其中绩效正常企业预测正确,而绩效非正常企业中有一家企业预测出现错误,预测结果准确率基本达到上节检测t-1年支持向量机集成学习方法模型的预测精度。
五、结 语
高新技术企业一般样本有限,特别是本文研究的样本是在创业板上市的高新技术企业。此外,用于评价高新技术企业绩效的数据指标较多,构建预测模型是一个高维度、非线性问题,支持向量机是一种人工智能算法,能够有效解决有限样本、高维数、非线性问题。Adaboost集成方法通过对不同子支持向量机赋予不同的权重经过多次迭代,得到最终的强预测器,能够显著提高模型预测精准度,这为研究高新技术企业绩效预测提供了新思路。
实证部分分别对样本企业进行了t-1年预测和t-2年预测,从预测结果准确率可以看出,t-1年预测和t-2年预测模型中,集成支持向量机预测精确度均高于支持向量机预测模型精确度。由此可得出构建集成支持向量机预测模型能够更有效地对企业绩效进行预测。
此外,通过随机抽取10家样本企业,实际应用所构建的t-1年支持向量机集成学习方法预测模型,利用这些企业2013年数据预测2014年绩效情况,得到的预测结果说明了集成支持向量机模型的有效性。
[1] Fan Palaniswanmim.A new approach to corporate loan default prediction from financial statements[C] .Proceedings of the computational finance/forecasting financial markets conference,2000.
[2] Kyung-Shik Shin,Taik Soo Lee,Hyun-jung Kim.An application of support vector machines in bankruptcy prediction model[J] .Expert Systems with Applications,2005,28(1):127-135.
[3] 张在旭,宋杰鲲,张宇.一种基于支持向量机的企业财务危机预警新模型[J] .中国石油大学学报:自然科学版,2006(04):132-136.
[4] 张晓琦.SVM算法在高新技术企业财务危机预警模型中的应用研究[J] .科技管理研究,2010(06):147-149
[5] 张震,汪斌强,梁宁宁,程国振.一种基于AdaBoost-SVM的流量分类方法[J] .计算机应用研究,2013(05):1481-1485
[6] Murphy,Sirgy M J.Measuring Corporate Performance by Building on the Stakeholders Model of Business Ethics[J] .Journal of Business Ethics,2002(35):143-162.
[7] 汤谷良,杜菲.试论企业增长、盈利、风险三维平衡战略管理[J] .会计研究,2004(11):31-37.
[8] 钱爱民,张新民.企业财务状况质量三维综合评价体系的构建与检验——来自我国A股制造业上市公司的经验证据[J] .中国工业经济,2011(03):88-98.
