基于PFC的废石胶结充填体破坏规律研究

马乾天，李长洪

（1.金属矿山高效开采与安全教育部重点实验室，北京100083；2.北京科技大学土木与环境工程学院，北京100083）

基于PFC的废石胶结充填体破坏规律研究

马乾天1，2，李长洪1，2

（1.金属矿山高效开采与安全教育部重点实验室，北京100083；2.北京科技大学土木与环境工程学院，北京100083）

为研究不同灰砂比下废石胶结充填体的破坏规律，对其进行了单轴压缩试验。结果表明，废石胶结充填体试样的失稳方式分为张开式和剪切式；在废石胶结充填体试样的峰值前应力—应变关系上，灰砂比对发生张开式失稳的试样影响较大，而对发生剪切式失稳的试样影响较小。运用基于细观颗粒流理论的PFC程序对废石胶结充填体模型进行单轴压缩模拟。结果表明，在应力—应变关系上，模拟结果与试验结果相一致；通过模型内部废石的位移情况可以揭示不同灰砂比下废石胶结充填体的失稳规律；通过粘结力分布情况得到废石胶结充填体不同失稳方式的原因。因此，PFC可以很好地应用于充填材料的选择与优化。

单轴压缩；废石胶结充填体；灰砂比；PFC

近年来许多矿山为减少损失，提高资源的利用率，会采用人工矿柱代替原生矿柱支撑顶板或上盘围岩。考虑到回采资源所带来的废料排放、环境恶化等诸多负面影响，同时，也为了节约成本，人工矿柱多利用矿山固体废料（尾砂、废石）作为其主要成分，配入胶结材料形成废石胶结充填体。同时人工矿柱作为矿体安全回采最重要的支撑结构，在井下回采复杂的外部力学环境下，一旦其破坏或失稳（诸如充填体顶底柱、充填体间柱、支撑上下盘的充填体），将造成顶板垮塌冒落、上下盘岩移，甚至诱发深部回采地压现象的发生，对安全回采形成严重的威胁。因此，对废石胶结充填体的力学性能和破坏规律的研究可以为充填材料选择、优化与其稳定性分析提供重要依据［1－2］。李永明等［3］通过试验对以矸石为充填料、水泥－水玻璃为胶结材料的充填体在充填采空区时的力学特性和影响因素进行了研究。徐俊明等［4］通过对以矸石－粉煤灰为充填材料的充填体压实过程中变形规律的研究来得到了该类充填体的最佳配比。史俊伟等［5］对充填料配比和膏体浓度对煤矸石膏体充填各性能指标的敏感程度进行了研究，并给出了各指标随影响因素的变化趋势。贺桂成等［6］研究了以废石、水泥和黄土为充填料的充填体强度特性。

同时，运用微细观理论对岩石、沥青类材料进行研究已经成为一种热门方法［7－9］。其中的颗粒离散元法（Particle Flow Code，PFC）中的平行粘结模型（Parallel Bond Model）已经在岩石、水泥类材料的研究中得到了广泛的认同。PFC程序通过离散元法来模拟球形颗粒的运动以及颗粒间的相互作用，并且在牛顿第二定律和力—位移定律基础上可以不设定本构关系，而只从细观尺度上来模拟材料中颗粒的大小及颗粒间的连接与摩擦等相互作用来建立宏观材料模型，从而揭示材料的本质属性。

所以，本文通过对不同灰砂比的废石胶结充填体试样进行单轴压缩试验来得到其应力—应变关系与破坏方式。然后通过PFC对不同灰砂比的废石胶结充填体模型进行单轴加载的模拟，将模拟结果与试验结果相对比，来达到研究不同灰砂比下废石胶结充填体破坏规律的目的。同时，也为充填材料的选择和优化提供一种新的方法。

1 试验条件和结果

1.1 试验条件

本文的试验系统采用中国科学院武汉岩土力学研究所研制的RMT－150C岩石力学试验系统，其最大荷载为1 000kN，活塞行程50mm，机架刚度5× 106N/mm。

废石胶结充填体试样由废石、水泥和尾砂制成。废石为千枚岩。由于许多矿山制作人工矿柱时并不是采用级配砾石，而是采用自行破碎的废石，导致废石粒径并不均匀，甚至有个别废石的粒径会很大。所以本文在制作废石胶结充填体试样时按粒径把废石分为两组，一组粒径为5～31.5mm，另一组粒径为31.5～50mm，其中粒径31.5～50mm的废石用量小于10%。用尾砂和325＃硅酸盐水泥制备砂浆，灰砂比（水泥︰尾砂）分为1︰4、1︰8和1︰12（矿山常用的三种配比），质量浓度75%。试样为圆柱体，尺寸为Φ75×150mm。模型浇筑7d后拆模，并养护28d。每种灰砂比的试样20个，一共制得60个试样。对养护好的试样进行单轴压缩试验。

1.2 试验结果

根据试验中试样的破坏方式将废石胶结充填体试样分为以下两种类型：如图1（a）所示，当试样中左右两部分的废石组合体以较大角度组合在一起时，试样会在这两部分废石组合体之间发生张开式失稳，下文称为I型；如图1（b）所示，当试样中上下两部分的废石组合体以较小角度组合在一起时，试样会在这两部分废石组合体之间发生剪切式失稳，下文称为Ⅱ型。图中中缝两侧的废石组合体为大粒径为主，中间夹杂着小粒径废石并以水泥－尾砂胶结而成的组合体。中缝为位于试件中间部位并贯穿大部分试件的水泥—尾砂胶结料层。同时，通过试验结果发现，灰砂比1︰4的试样在中缝角度大于58°时发生张开式失稳，小于58°时发生剪切式失稳；灰砂比1︰8的试样在中缝角度大于56°时发生张开式失稳，小于56°时发生剪切式失稳；灰砂比1︰12的试样在中缝角度大于55°时发生张开式失稳，小于55°时发生剪切式失稳。可见，灰砂比对试样失稳方式的影响不大。

图1 废石胶结充填体试样内部结构Fig.1 Internal structure of cemented waste rock backfills specimens

图2 为两类试样的在三种灰砂比下的应力—应变曲线，其中I型试样选择的是中缝在60°～70°的试样的应力—应变曲线，Ⅱ型试样选择的是中缝在30°～40°的试样的应力—应变曲线。从图中可以看出，I型试样随着灰砂比的降低，除了强度的降低外，岩性也在逐渐变差，渐渐失去废石胶结充填体在破坏后仍能保持一定的承载能力这一特性。Ⅱ型试样随着灰砂比的降低，只表现出强度的降低，而岩性并没有变差，仍保留着废石胶结充填体在破坏后保持一定的承载能力这一特性。另外，灰砂比1︰4的I型试样在峰值前存在一个“台阶”状阶段，而其他类型的试样都没有这一现象。可见废石胶结充填体的峰值前应力—应变关系和峰值后承载能力受到水泥—尾砂胶结料和废石共同影响，其中I型结构的废石胶结充填体受灰砂比的影响较大。

图2 两种类型试样应力—应变曲线Fig.2 Stress－strain curves of two types of specimens

2 PFC模拟

2.1 颗粒流理论简介

颗粒流理论是由Cundall和Strack在离散元法的基础上引入分子动力学建立的，是一种侧重于用细观力学来解释材料的损伤断裂机理的理论［10］。该理论不仅能分析材料从线弹性阶段到断裂破坏的大变形过程，还能直观地给出材料中裂纹的张开、扩展和贯通过程，目前在研究岩石、水泥类材料的力学与工程特性中应用的越来越为广泛。PFC便是基于该理论的程序，它在整个模拟的过程中提供了两种基本模型：接触粘结模型和平行粘结模型［11］。其中，接触粘结模型是点接触，不能传递力矩。平行粘结模型（见图3）可以模拟两相邻颗粒间的附着胶凝物质。本文采用平行粘结模型。

平行粘结模型的接触处存在具有一定面积和刚度的粘结，可以限制颗粒旋转并传递力与力矩。在荷载作用下，平行粘结中的应力可以通过式（1）来得到：

当法向应力超过或者切向应力超过时，平行粘结破坏，分别产生张拉型微裂纹或剪切型微裂纹。

2.2 模型的建立

PFC模拟的模型式样和尺寸与试验用式样的尺寸保持一致，为尺寸Φ75×150mm的圆柱体，如图4（a）所示，即为废石胶结充填体模型的外观，其中灰色球体为水泥－尾砂胶结料颗粒。通过调用PFC建立clump的功能，在模型中构建废石。废石粒径与试验用废石粒径相同，形状为不规则多面体。废石间缝隙为5～10mm。按照模型中中缝的角度，建立了两种模型，它们的中缝角度分别为60°～70°（A型）和30°～40°（B型）。如图4所示，为两类模型内部废石结构图，图中黑色球体为废石颗粒。由于本文的模拟采用平行粘结模型，其细观参数标定过程非常复杂，一般通过相同加载速率条件下模型的静态单轴压缩下数值与室内试验的宏观弹性模量、峰值强度、泊松比等宏观性质进行匹配［12－13］。本文通过在相同加载速率条件下分别对废石（千枚岩）和不同灰砂比的水泥－尾砂胶结充填体模型进行静态单轴压缩下数值与室内试验的宏观参数配比，从而得到了其各自的细观力学参数（见表1）。

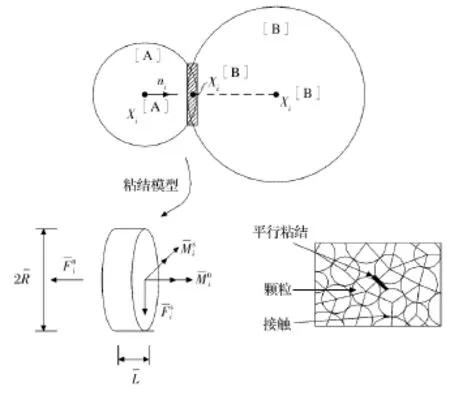
图3 平行粘结模型Fig.3 Parallel bond model

表1 材料细观力学参数Table 1 Mesomechanics parameters of different materials

图4 PFC模型内外部结构Fig.4 External and internal structure of PFC models

2.3 模拟结果及分析

图5中（a）和（b）分别为A型和B型模型与对应的I型和Ⅱ型试样的应力—应变曲线对比图。可以看出，PFC模拟结果与试验结果较为吻合。灰砂比1︰4的废石胶结充填体在发生张开式失稳时，无论是试验结果还是模拟结果都在峰值前存在一个“台阶”状的阶段。如图6（a）所示，在模拟过程中对A型模型中缝两侧的1号和2号废石中所有颗粒进行了位移的监测。通过1号和2号废石中所有颗粒位移的平均值来表示其整体位移。如图6所示，灰砂比1︰4的A型模型在进入“台阶”状阶段前，1号废石的位移要远远大于2号废石的位移，而进入“台阶”状阶段后，1号废石的位移速率突然变为非常缓慢而2号废石的位移速率却迅速增加，两废石的位移变化情况与“台阶”状阶段的出现相吻合。通过1号废石与2号废石的位移情况，再结合图7中“台阶”状阶段前后模型内部废石结构的变化情况可以看出，废石胶结充填体内不同部位在不同应力水平开始剧烈破坏是“台阶”状阶段出现的原因。这一过程实际上是一个随着废石结构改变导致新结构开始起承载作用的过程。从图6和图7中也可看出，随着灰砂比的降低，原先分先后剧烈张开的各部位逐渐变为一起张开，渐渐的失去图6（b）这种情况。同时图8也给出了B型模型破坏的内部废石结构。

图5 模拟结果与试验结果对比Fig.5 Comparison of simulation results and experimental results

图6 灰砂比1︰4的A型模型内部结构变化情况Fig.6 Changes of internal structure of model A with cement－sand ratio 1︰4

图9 为两类模型的粘结力（connect force）分布图。如果模型中的颗粒之间存在粘结力，则以黑色连线表示；如果模型在计算中颗粒之间的平行粘结发生破坏，则粘结力消失，黑色连线便会消失，从而形成图中的空白区域。可以看出，B型模型颗粒间粘结力的断开主要集中在中缝处，而A型模型粘结力的断开除了集中在中缝处，还出现在图中圆圈处，使得模型内中缝两侧的废石向外倾倒，最后呈张开式失稳的形式。

图7 不同灰砂比下A型模型废石位移Fig.7 Displacement of waste rocks of model A with various cement－sand ratios

图8 B型模型破坏方式Fig.8 Failure mode of model B

图9 粘结力分布图Fig.9 Distribution of cohesive force

3 结论

通过废石胶结充填体试样的单轴压缩试验发现，根据试样中缝的角度不同，试样可以分为张开式失稳和剪切式失稳。通过PFC程序建立废石胶结充填体模型，并对其进行单轴压缩试验的模拟。结果表明：无论从应力—应变关系还是灰砂比对破坏方式的影响上，模拟结果都与试验结果有着相似的规律。并通过模型中废石的位移变化规律可以发现，灰砂比1︰4的废石胶结充填体在发生张开式失稳时存在的“台阶”状阶段，实际上是随着废石结构改变导致新结构开始起承载作用的阶段。随着灰砂比的降低，这一现象消失。通过粘结力分布情况发现模型最后呈张开式失稳是由于中缝两侧的废石周围出现大量平行粘结破坏从而导致其向外倾倒造成的。同时，也证明PFC可以很好地应用于充填材料的选择和优化上。

［1］王新民，彭续承 .块石胶结充填工艺的试验研究［J］.化工矿山技术，1996，25（5）：16－18.

［2］郭利杰，杨小聪 .废石尾砂胶结充填试验研究［J］.武汉理工大学学报，2008，30（11）：75－78，112.

［3］李永明，刘长友，邹喜正，等.急倾斜薄煤层胶结充填开采合理参数确定及应用［J］.煤炭学报，2011，36（增刊）：7－12.

［4］徐俊明，张吉雄，黄艳利，等.充填综采矸石－粉煤灰压实变形特性试验研究及应用［J］.采矿与安全工程学报，2011，28（1）：158－162.

［5］史俊伟，魏中举，刘庆龙，等.基于正交试验的煤矿安全开采充填材料配比优化研究［J］.中国安全科学学报，2011，21（6）：111－115.

［6］贺桂成，刘永，丁德馨，等 .废石胶结充填体强度特性及其应用研究［J］.采矿与安全工程学报，2013，30（1）：74－79.

［7］陈俊，黄晓明 .采用离散元方法评价集料的骨架结构［J］.东南大学学报：自然科学版，2012，42（4）：761－765.

［8］张超，展旭财，杨春和 .粗粒料强度及变形特性的细观模拟［J］.岩土力学，2013，34（7）：2077－2083.

［9］刘先珊，董存军 .三维颗粒流数值模型的胶结砂岩力学特性［J］.重庆大学学报，2013，36（2）：37－44.

［10］Cundall P A，Strack O D.A discrete numerical model for granula assemblies［J］.Geotechnique，1979，29（1）：47－65.

［11］Itasca Consulting Group.PFC2D（particle flow code in 2 dimensions）fish in PFC2D［R］.Minneapolis，USA：Itasca Consulting Group，2008.

［12］Lee H，Jeon S.An experimental and numerical study of fracture coalescence in pre－crached specimens under uniaxial compression［J］.International Journal of Solids and Structures，2011，48：979－999.

［13］黄达，岑夺丰，黄润秋 .单裂隙砂岩单轴压缩的中等位移率效应颗粒流模拟［J］.岩土力学，2013，34（2）：535－545.

Study on the failure law of cemented waste rock backfills based on PFC

MA Qiantian1，2，LI Changhong1，2
（1.State Key Laboratory of High－Efficient Mining and Safety of Metal Mines，Ministry of Education，Beijing 100083，China；2.School of Civil and Environmental Engineering，University of Science and Technology Beijing，Beijing 100083，China）

In order to study the failure law of cemented waste rock backfills with various cement－sand ratios，uniaxial compression test is carried out.The results show that the failure mode of cemented waste rock backfills specimen can be divided into tensor failure and shear failure.Specimens with tensor failure can be greatly affected by cement－sand ratio on the stress－strain relationship of pre peak.In order to simulate the influence on the failure law of cemented waste rock backfills caused by cement－sand ratio in uniaxial compression test，PFC is used.The results show that the simulated results are consistent with the experimental results on the stress－strain relationship.The failure law of cemented waste rock backfills with various cement－sand ratios can be revealed by the displacement of waste rocks in models.The reasons of different failure modes of cemented waste rock backfills can be revealed by the distribution of connect force.Therefore，PFC can be used in selection and optimization of filling materials.

uniaxial compression；cemented waste rock backfill；cement－sand ratio；PFC

TD313

A

1671－4172（2015）05－0060－05

国家自然科学基金青年科学基金资助项目（51304083）

马乾天（1987－），男，博士研究生，土木工程专业，主要研究方向为矿山岩石力学。

10.3969/j.issn.1671－4172.2015.05.012