空气自由场中强爆炸冲击波传播二维数值模拟

姚成宝，李 若，田 宙，郭永辉

(1.北京大学数学科学学院，北京 100871； 2.西北核技术研究所，陕西 西安 710024； 3.北京大学应用物理与技术研究中心，北京 100871)



空气自由场中强爆炸冲击波传播二维数值模拟

姚成宝1,2，李 若1,3，田 宙1，郭永辉1

(1.北京大学数学科学学院，北京 100871； 2.西北核技术研究所，陕西 西安 710024； 3.北京大学应用物理与技术研究中心，北京 100871)

编写了适用于模拟具有高密度比、高压力比的强激波问题的二维柱对称多介质流体计算程序。利用有限体积方法求解流体的Euler方程组，采用level set方法捕捉爆炸产物与空气的运动界面，并通过求解物质界面两侧Riemann问题的精确解来计算爆炸产物与空气之间的数值通量。研制了三角形网格自适应技术来实现网格的自动加密和粗化，在保证捕捉激波峰值的前提下有效地提高了计算效率。利用计算程序对1 kt TNT当量的空气自由场强爆炸问题进行数值模拟，计算得到的峰值超压、冲击波到达时间等物理参数与点爆炸理论结果基本一致。

爆炸力学；空中强爆炸；level set；Riemann问题；网格自适应；自由场；冲击波

空中爆炸[1]是指炸药、炮弹等在距地面或水面一定高度处的爆炸。随着计算机技术和计算理论的快速发展，数值模拟在该领域内的研究起到越来越重要的作用[2-3]。和常规炸药相比，强爆炸产生的初始压力更高，随传播距离衰减更慢，杀伤破坏距离更远，数值模拟的难度更大。

针对空中强爆炸问题的强对流性，本文中选择基于欧拉坐标系下的多介质流体计算模型模拟冲击波的传播过程。文献[4]中认为爆炸产物与空气的界面最初是分开的，只是随后由于爆炸产物的脉动作用，特别是由于界面周围产生涡流作用，使得界面逐渐模糊，最后与空气混合在一起。文献[4]的实验结果表明，对爆炸破坏作用具有实际意义的只是第一次的膨胀和压缩过程。基于上述观点，本文中采用level set方法捕捉爆炸产物与空气的界面，并认为界面两侧的物质不发生相互融合。大量的数值结果表明[5-7]，在物质界面两侧，由于爆炸产物与空气具有不同的状态方程，且密度、压力相差巨大，需采取合适的方法来处理界面上的接触间断，否则会产生强烈的非物理振荡。本文中通过求解Riemann精确解来获得界面上接触间断两侧的物质状态，并以此求解界面上的数值通量，以避免非物理振荡。

在空中强爆炸冲击波传播数值模拟过程中，为准确捕捉冲击波压力峰值，本文中采用网格自适应技术来实现网格的自动加密和稀疏；利用计算程序对1 kt TNT当量空中强爆炸产生的冲击波传播过程进行数值模拟，将计算得到的冲击波参数与点爆炸理论结果[8]进行对比。

1 控制方程和状态方程[9]

由于空中强爆炸问题本身具有的对称性，本文采用二维柱对称计算模型来进行计算。控制方程为：

(1)

式中：ρ表示密度，u和v表示方向r和z方向的速度，E表示总能量密度，p表示压力。

爆炸产物和空气均采用γ律状态方程描述：

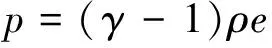
(2)

式中：γ为比热比；对于强爆炸产物，γ=1.2；对于空气，γ=1.4。e为比内能，且满足：

(3)

2 计算方法

2.1 level set方法[10-12]

level set方法的主要思想是引入level set距离函数φ(x,t)，把随时间运动的物质界面Γ(t)定义为距离函数的零等值面。在每个时刻，只要求出距离函数φ(x,t)的值，就可以知道物质界面的位置。level set函数的演化方程为：

(4)

式中：φt、φx和φy分别为φ对t、x和y的偏导数。在计算过程中，为保持φ(x,t)始终是x点到界面Γ(t)的符号距离，需要对φ(x,t)进行重新初始化：

(5)

式中：φ0为重新初始化前的φ(x,t)的值，且

(6)

式中：ε为一个任意小的正数。

2.2 Riemann问题求解[13-14]

图1 Riemann问题解的类型Fig.1 Solution type of the Riemann problem

律状态方程的Riemann问题为求解式(7)所示的多介质Euler方程组的初值问题：

(7)

式中：下角标1和2分别表示接触间断左侧和右侧。

这种初始时刻的间断是不稳定的，在t>0时会立即分解为图1所示的波系结构。其中,w表示线性退化的接触间断波；w1和w2分别表示接触间断两侧的非线性波(根据初值条件的不同，可能是稀疏波或者激波)；ρI1和ρI2分别为接触间断上w左侧和右侧的密度。在接触间断两侧，压力和速度保持不变，而密度发生间断。记W=(ρ,u,p)T，则压力p满足：

(8)

其中,

(9)

(10)

(11)

利用牛顿迭代法对式(8)进行迭代求解，可得到界面上的最终压力p。界面上的速度u的表达式为

(12)

3 数值离散方法

3.1 守恒方程组的离散求解

采用有限体积方法来离散求解守恒方程组，在每个网格单元τ上从tn到tn+1时刻对式(1)进行积分，可得：

(13)

(14)

式中：Ut、Fx、Gy分别为U、F、G对t、x、y的偏导数，Ω为网格单元的体积。利用散度定理，可得：

(15)

式中：∂τ为τ的表面，S为表面积。对于包含2种流体的混合单元，除了需要计算单元边界上的数值通量外，还需要在物质界面上利用Riemann问题的解来计算2种流体在界面上的数值通量。

3.2 level set方程求解

本文中利用特征线方法来数值求解level set函数的演化方程，将式(4)转换成:

(16)

根据特征线方法的思想，只需知道tn+1时刻网格顶点Xi上的流体质点在tn时刻的位置 ，就可以得到tn+1时刻的level set函数在Xi处的值φn+1(Xi)。具体求解过为：

(17)

(18)

式中：Vn[X(tn)]表示tn时刻X(tn)处流体质点的速度。

图2 网格自适应示意图Fig.2 Mesh adaption

利用文献[15]中的显式正系数格式来进行求解level set函数的重新初始化方程(5)，保持φ(x,t)始终是x点到界面Γ(t)的符号距离。

3.3 网格自适应技术

为了有效地捕捉激波峰值，并尽可能减少计算量，本文中采用网格自适应技术。根据相邻网格的压力梯度来构造自适应指示因子，在压力变化剧烈的地方加密网格，在变化平缓的地方对网格进行粗化。典型的网格自适应如图2所示。

由图2可知，在冲击波波阵面附近，为捕捉激波峰值，网格被剧烈的加密；而在冲击波波阵面后以及冲击波尚未达到的地方，网格非常稀疏。

4 算 例

对1 kt TNT当量空中强爆炸产生的冲击波传播过程进行数值模拟，并将计算得到的冲击波参数与点爆炸理论结果[8]进行对比。

(1) 冲击波压力等值线图。

计算得到不同时刻的冲击波压力等值线如图3所示。

图3 不同时刻的冲击波压力等值线图Fig.3 Pressure contours at different time

(2) 冲击波参数。

将计算得到的不同爆心距(r)的冲击波超压峰值(pop)、正压冲量(I)、冲击波到时(ts)和正压作用时间(Δt)等冲击波参数与点爆炸理论结果进行比对，如图4～7所示。

图4 峰值超压Fig.4 Peak overpressure

图5 正压冲量Fig.5 Overpressure impulse

图6 冲击波到时Fig.6 Arrival time

图7 正压作用时间Fig.7 Positive time duration

从图4～7可知，程序计算得到的峰值超压、冲击波到时与点爆炸理论结果基本一致，正压作用时间略有差别。由于点爆炸理论中没有给出正压冲量的结果，这里只给出程序的计算结果。

(3) 冲击波超压时间历程曲线。

计算得到不同爆心距的冲击波超压(po)历程曲线，如图8所示。从图8可知，对离爆心一定距离的观察点，当冲击波到达时，空气压力迅速上升至峰值；冲击波过后，空气压力逐渐降低；当爆炸产物过度膨胀形成的负压稀疏波到达时，空气呈稀疏状态，空气压力逐渐下降至负压。随后由于爆炸产物的脉动作用，该处再次形成二次激波。如此反复，直至最后恢复至初始压力。从图8中给出的距爆心为200 m和300 m处的冲击波超压历程来看，计算得到的冲击波超压曲线能够正确地描述空中强爆炸时某固定位置处冲击波的正压、负压以及二次激波，表明程序的计算合理，结果可信。

5 结 论

针对空中强爆炸问题的特点，研究了适合计算强对流问题的数值计算方法，在此基础上编写了相应的二维多介质流体计算程序。其中，采用有限体积方法求解流体控制方程，利用level set方法捕捉流体的运动界面，并通过求解物质界面两侧的Riemann问题精确解来计算物质界面两侧的数值通量。计算过程中采用了网格自适应技术，在捕捉激波峰值的前提下，有效地减小了计算量，提高了计算效率。

计算了1 kt TNT当量的空中强爆炸问题，模拟了冲击波在空气自由场中的传播过程，给出了从爆炸源区附近到1 km距离处各爆心距的超压峰值、正压冲量、冲击波到时和正压作用时间等冲击波参数，计算结果与点爆炸理论结果基本一致，说明本文程序采用的计算方法能够应用于空中爆炸等强对流问题的数值模拟。

[1] 奥尔连科 Л П.爆炸物理学[M].孙承纬,译.北京:科学出版社,2013,456-463.

[2] 张洪武,何扬,张昌权.空中爆炸冲击波地面载荷的数值模拟[J].爆炸与冲击,1992,12(2):188-198. Zhang Hong-wu, He Yang, Zhang Chang-quan. Numerical simulation on ground surface loading of shock wave from air explosion[J]. Explosion and Shock Waves, 1992,12(2):188-198.

[3] 岳鹏涛,徐胜利,彭金华.FAE爆炸波对地面目标作用的三维数值模拟[J].爆炸与冲击,2000,20(2):195-201. Yue Peng-tao, Xu Sheng-li, Peng Jin-hua. 3D numerical simulations on the interaction between FAE blast waves and ground targets[J]. Explosion and Shock Waves, 2000,20(2):195-201.

[4] 北京工业学院.爆炸及其作用[M].北京:国防工业出版社,1979.

[5] Liu T G, Khoo B C, Yeo K S. Ghost fluid method for strong shock impactingon material interface[J]. Journal of Computational Physics, 2003,190(2):651-681.

[6] Fedkiw R P, Aslam T, Merriman B,et al. A non-oscillatory eulerian approach to interfaces in multimaterial flows: The ghost fluid method[J]. Journal of Computational Physics, 1999,152(2):457-492.

[7] Colella P, Glaz H M. Efficient solution algorithms for the Riemann problem for real gases[J]. Journal of Computational Physics,1985,59(2):264-289.

[8] 乔登江.强爆炸物理概论(上册)[M].北京:国防工业出版社,2003:51-55.

[9] 杨秀敏.爆炸冲击现象数值模拟[M].合肥:中国科学技术大学出版社,2010:122-125.

[10] Osher S, Sethian J A. Fronts propagating with curvature dependent speed: Algorithms based on Hamilton-jaccobi formulations[J]. Journal of Computational Physics, 1988,79(1):12-49.

[11] Sussman M, Semerka P, Osher S. A level set approach for computing solutions to incompressible two-phase flow[J]. Journal of Computational Physics, 1994,114(4):146-159.

[12] 张军,赵宁,任登凤,等.level set方法在自适应Catersian网格上的应用[J].爆炸与冲击,2008,28(5):156-161. Zhang Jun, Zhao Ning, Ren Deng-feng, et al. Application of the level set method on adaptive cartesian grids[J].Explosion and Shock Waves, 2008,28(5):156-161.

[13] Eleuteuo F T. Riemann solvers and numerical methods for fluid dynamics[M]. First Edition. Springer, 2009:16-123

[14] 刘儒勋,舒其望.计算流体的若干新方法[M].北京:科学出版社,2003:121-130

[15] Di Y N, Li R, Tang T, et al. level set calculations for incompressible two-phase flows on a dynamically adaptive grid[J]. Journal of Scientific Computing, 2007,31(1/2):75-98.

(责任编辑 王小飞)

Two dimensional simulation for shock wave produced by strong explosion in free air

Yao Cheng-bao1, 2, Li Ruo2, Tian Zhou1, Guo Yong-hui1

(1.SchoolofMathematicalSciences,PekingUniversity,Beijing100871,China; 2.NorthwestInstituteofNuclearTechnology,Xi’an710024,Shaanxi,China; 3.CenterofAppliedPhysicsandTechnology,PekingUniversity,Beijing100871,China)

Aimed to simulate the propagation of blast wave with high density ratio and high pressure ratio produced by strong explosion in the air, a two dimensional numerical program is written in which the problem is treated as a two-medium compressible flow with sharp material interface in Eulerian grids. In this method, the finite volume method is used to solve the Euler equations, level set method is used to capture the moving interface, and the numerical flux across the interface is calculated by exactly solving the Riemann problem. Mesh adaption technique in triangle meshes is adopted to refine or coarsen the meshes which can both capture the peak overpressure and improve the computational efficiency. One kiloton nuclear charge of strong explosion in free air is simulated. The shock wave parameters, including peak overpressure, shock arrival time and so on, are in consistence with the point explosion theory, which show the accuracy and efficiency of the numerical methods.

mechanics of explosion; strong explosion in air; level set; Riemann problem; mesh adaption; free air; shockwave

10.11883/1001-1455(2015)04-0585-06

2013-12-04；

2014-07-09

姚成宝(1984- )，男，博士研究生，助理研究员，yaocheng@pku.edu.cn。

O381 国标学科代码： 13035

A