预折纹管在低速冲击载荷作用下的能量吸收

王 博，周才华，由 衷

(1.大连理工大学工业装备结构分析国家重点实验室，辽宁 大连 116024； 2.大连理工大学工程力学系，辽宁 大连 116024； 3.牛津大学科学工程系，英国 牛津 OX13PJ)



预折纹管在低速冲击载荷作用下的能量吸收

王 博1,2，周才华1,2，由 衷3

(1.大连理工大学工业装备结构分析国家重点实验室，辽宁 大连 116024； 2.大连理工大学工程力学系，辽宁 大连 116024； 3.牛津大学科学工程系，英国 牛津 OX13PJ)

为了降低结构的初始载荷、增加有效塑性变形面积，进而提高其吸能效率，研究一种以新型的预折纹管，在普通管的管壁上引入特别设计的折角。基于有限元软件ABAQUS/EXPLICIT的数值分析验证了预折纹在低速冲击载荷作用下可以引导预期的大变形模式，预折纹管的这种大变形模式相较于普通方管的对称变形模式有更低峰值载荷和更高的平均载荷。通过低速落锤实验获得了与有限元模拟结果相似的载荷-位移曲线和变形模式，验证了数值结果的可信性和预折纹方管的高效吸能特点。

固体力学；能量吸收；低速冲击实验；薄壁结构；耐撞式设计

汽车碰撞会给公众的生命和财产造成的巨大损失，安装专门设计的能量吸收装置是解决碰撞问题的主要途径[1]。能量吸收与耗散的方式有很多种，薄壁金属是最常见的能量吸收结构，大量的研究关注于薄壁金属在冲击作用下的力学性能[2]。不仅汽车制造业[3]，金属薄壁结构在航空航天工业[4]、火车制造业[5]以及造船业[6]等领域的应用也十分广泛，例如：杨嘉陵等[7]研究了直升机的坠落碰撞，直升机机体可看成是金属薄壁结构，直升机在垂直坠落时薄壁机身可以吸收高达40%的动能；李玉龙[8]对民用飞机与鸟碰撞的研究现状作了较为详细的描述，为了减小鸟与飞机的高速冲击带来的伤害，许多以金属薄壁为基础的结构被实验验证为效果较好的结构类型。多年来，研究人员提出了各种各样的金属薄壁结构并对其吸能效果做了相关研究[9]，其中很多的研究成果已经运用到工业生产中，并取得了良好的效果。最常见的普通方管、圆管、多胞管以及泡沫填充管等[10-17]已经被研究得很透彻，但是这些吸能构件在轴向冲击载荷作用下的变形模式极大地限制了能量吸收的效果，所以提出吸能效果更好的结构成为了众多研究人员研究的目标。

J.Song等[18]将方管发生对称变形时的中间模态设计成一种折纹引入到方管的管壁上，这种折纹一方面可以引导方管发生稳定的对称变形模式，另一方面可以有效降低峰值载荷。J.Ma等[19]设计了一种新型的预折纹管，这种折纹的引入能够引导预折纹管在轴向准静态载荷作用下发生一种特殊的变形模式，相较于普通方管发生的对称变形，预折纹管的这种特殊的变形模式一方面能够降低初始载荷，另一方面能够提高平均载荷。J.Ma等[20]研究了预折纹梁的横向冲击效果，发现这种预折纹梁在横向载荷作用下有会发生2种不同的变形模式，这2种变形模式均有很好的吸能效果。

本文中对于折纹管和普通方管在低速冲击载荷作用下的力学行为进行有限元模拟，通过有限元计算结果分析预折纹管的吸能机理；并制作预折纹管试件，进行低速落锤实验，通过实验验证有限元计算结果的可信度。

1 模型介绍

轴向冲击载荷作用下的峰值载荷Fp和平均载荷Fm是评价吸能装置吸能效率高低的主要指标，Fm可以由能量E除以有效压缩距离δ得到，本文中除了考虑吸能构件的峰值载荷和平均载荷，还将引入压缩力效率(ηCFE)作为评价吸能效率的主要指标，压缩力效率由平均载荷和峰值载荷的比值定义，充分考虑了峰值载荷和平均载荷2个指标，可以作为评价吸能构件吸能效率高低的综合指标。由于本文中与预折纹管进行吸能性能对比的普通方管与预折纹管有相同的表面积(即具有相同的质量m)，所以平均载荷与比吸能(ηSEA)在吸能性能对比的效果上一致。ηCFE和ηSEA表达式为：

(1)

理想的吸能构件在冲击时具有较低的峰值载荷和较大的平均载荷。普通方管在轴向冲击载荷的作用下通常会发生对称变形，在这种变形模式的限制下，峰值载荷往往很高而平均载荷却很低。所以通过改进方管的几何构型来改变其变形模式成为提高吸能性能的主要办法。

普通方管的对称变形之所以具有较高的峰值载荷，是由于变形初始的轴向刚度过大，而在管壁上引入缺陷可以较为明显的降低轴向刚度，所以在普通方管的管壁上引入一种特殊折角(如图1所示)，预想这种折角也可以起到与缺陷相同的效果；另外，根据T.Wierzbicki的超折叠单元理论[21]，普通方管在发生对称变形过程中移动塑性铰线所吸收的能量占吸收总能量的2/3，而普通方管的一个标准段只能产生8条移动塑性铰线，本文中在普通方管的管壁上引入的特殊折角能使一个标准段上的塑性铰线数量增加到16条，预想这种折角能够极大的提高方管的能量吸收，即提高平均载荷。

图1 预折纹管模型Fig.1 Model of pre-folded tube

在普通方管管壁上引入特殊折角后的预折纹管的一个单元(标准段)，如图1(a)所示，其中单元的上下边界为正方形截面，其边长b为定值60 mm，中间截面的形状为八边形，c为折纹长度，单元的高为h，厚度为1 mm。预折纹管可以由平面矩形经过折叠形成，如图1(c)所示，其中实线代表折纹凸起，虚线代表折纹凹陷，预折纹管的这种特殊的几何构型使其在实际生产过程中用简单的冲压和焊接即可完成成型工艺。预折纹管的二面角θ与单元沿轴向展开铺平后的高度l以及c的几何关系为：

(2)

2 数值模拟

首先采用基于有限元软件的数值计算验证预折纹管在低速冲击时的变形机理，对比这种大变形模式与普通方管的对称变形模式的差异，讨论这种变形机理对预折纹管的能量吸收效率的影响。

2.1 材料实验

图2 材料测试Fig.2 Material tensile test

为了保证数值模拟结果的真实性，需要设计材料实验以获取材料的力学性能。图2(a)为实验试件，材料为Q235钢，有效长度为64 mm，有效横截面尺寸为1 mm×5 mm。由于预折纹管在制作的过程中需要加热以消除焊接预应力，所以为了保证材料试件与预折纹管的材料力学性能一致，在预折纹管和普通方管加热时将材料试件同时放入高温炉中加热，冷却后再对试件进行拉伸实验，得到试件的力-位移曲线，对力-位移曲线进行数据处理即可以得到材料的应力(σ)-应变(ε)曲线，见图2(b)。

2.2 有限元模型参数设置

图3 网格收敛性验证Fig.3 Convergence tests

采用有限元分析软件ABAQUS/EXPLICIT的显式动力学数值分析预折纹管在低速落锤实验中的力学性能。为了与实验作对比，数值计算的模型尺寸、边界、载荷、材料(Q235钢)等都尽量与实验中保持一致。预折纹管模型由2个标准段组成，每个标准段高为60 mm，标准段的截面为正八边形，即c=30 mm。作为对比的普通方管的横截面为60 mm的正方形，总高为120 mm，厚度为1 mm。在距离普通方管顶端8 mm的地方引入高度和深度都为1.5 mm的一对槽型缺陷。实验中的冲击台和重锤在有限元模型中用刚性板来模拟，预折纹管的底边与模拟冲击台的刚性板之间用Tie约束，模拟重锤的刚性板被赋予与重锤相同的质量。在有限元模型中，预折纹管和普通方管管壁材料的本构关系由2.1节中的材料实验得到(如图2(b)所示)；另外，根据Cowper-Symonds模型模拟材料的应变率强化效应，Q235钢的应变率强化参数C和P分别为114 s-1和5.56[22]。模拟重锤的刚性板被赋予与7 m/s的初始速度，与实验中重锤的初始速度一致。预折纹管管壁自身采用self-contact接触类型，管壁与刚性板之间采用surface-to-surface contact接触类型。有限元模型的网格采用四节点曲面薄壳SR4单元，单元面内有1个积分点，厚度方向有5个积分点，设置有限元网格种子ls=3 mm，一方面考虑到有限元计算的精度，另一方面考虑到计算时间成本(图3)，因为后续研究预折纹管的几何尺寸敏感性和优化工作还需要大量的数值计算。从图3可以发现，ls<3.5 mm时，能量(E)波动趋于平缓(能量波动大小(51 J)与能量最大值(1 409 J)之比为3.6%)，ls<3 mm时，计算时间(tcpu)有明显增大。另外，在ABAQUS计算中，壳单元的最小边长应大于壳厚，以避免与最小壳单元相邻的两个单元之间产生实际并不存在的自接触[23]，而当网格种子为3 mm时，只保证几何特征边上的网格大小为3 mm左右，有限元中的最小网格尺寸已经接近于壳厚1 mm。

2.3 数值结果

图4和图5为预折纹管与普通方管的变形模式与云图。可以看出普通方管发生了预期的对称变形模式，而预折纹管则发生了预期的大变形模式，折角的引入强制预折纹管的折叠段数目等于标准段数目，每个标准段的移动塑性铰线数量从普通方管的8条增加到预折纹管的16条，移动塑性铰线数量增加导致发生塑性形变的面积增加；而普通方管在变形中出现了3个折叠段，发生塑性形变的区域局限于普通方管的折角周围的小部分区域，大部分区域的材料没有发生塑性形变，从而限制了能量的吸收。图6为模拟得到载荷F和能量E随位移d的变化曲线。可以看出，折角的引入使峰值载荷从普通方管的45.99 kN降低到预折纹管的25.4 kN，降低了44.8%；而在相同加载位移处(70 mm)的平均载荷也从普通方管的14.47 kN提高到预折纹管的19.85 kN，提高了37.2%；压缩力效率从普通方管的0.31提高到预折纹管的0.78，提高了151.6%。

图4 数值模拟变形模式Fig.4 Shape change patterns via simulation

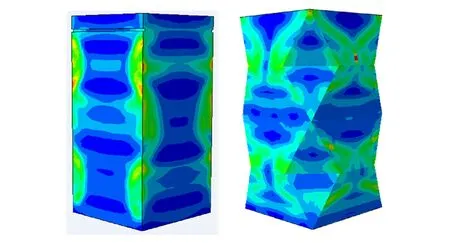
图5 数值模拟塑性变形云图Fig.5 Plastic zone via simulation

图6 预折纹管与普通方管模拟结果对比Fig.6 Numerical comparison between the pre-folded tube and the ordinary squeare tube

预折纹管的吸能性能之所以有如此大的提高，与预折纹管在失效时发生的特殊变形模式有关，而这种变形模式的发生则与预折纹管的几何构型有关。相比普通方管，预折纹管只在普通方管的4条棱上引入了特殊折角。首先，这种折角的引入使棱边和侧面与横截面的方向由普通方管的垂直变成了倾斜，垂直的几何结构的轴向刚度非常大，而倾斜的几何结构的轴向刚度则大幅减小，刚度越大，冲击时反力也就越大，所以预折纹管的峰值载荷较普通方管降低了44.8%，普通方管在峰值载荷之后的载荷值急剧下降也正是由于其几何形状不再保持垂直；其次，折角的引入可以使一个标准段的棱的数量从8条变为16条， 这种倾斜的棱边在预折纹管失效变形的初始阶段将因为应力集中效应而进入塑性，形成塑性铰线，而且倾斜的棱在竖直方向受力时由于横向方向受力不均衡而更加容易移动成为移动塑性铰线，移动塑性铰线数目的增加导致其在移动时扫过的总面积大幅增加，塑性铰线的扫掠会使管壁的某些区域连续发生两次弯曲变形[24]，这种弯曲变形会使远离管壁中性层的材料发生大变形而进入塑性，所以塑性铰线扫过的区域将会发生塑性变形而吸收能量，如图5中的应力云图所示，在这种机理下，预折纹管吸收的能量也比普通方管增加了37.2%。

3 实验验证

通过有限元数值计算结果验证折角能够引导预折纹管发生特殊变形，然而数值计算往往偏于理想，实际情况下的预折纹管在低速冲击载荷作用下是否能发生与有限元计算结果一样的变形模式，数值计算所得到的载荷和能量数值是否准确，都需要通过实验进行进一步验证。通过3个部分来阐述实验的过程及结果分析。

3.1 试件制作

制作预折纹管试件的矩形钢板尺寸为130 mm×120 mm，实验中预折纹管的尺寸与数值模拟中模型的尺寸一致。预折纹管的制作分为冲压、折叠、焊接、热处理4个部分，制作流程如图7所示。为了减小冲压和折叠的预应力以及焊接产生的残余应力，热处理时需要将试件(包括预折纹管和普通方管)加热到800 ℃，并保持2小时，然后慢慢冷却。

图7 预折纹管的制作流程Fig.7 The pre-folded tube manufacturing process

3.2 实验器材

图8为低速落锤实验使用的落锤式冲击实验机。落锤质量为64 kg，最大冲击速度为10 m/s。可以通过操作系统设定落锤与试件的垂直高度或者落锤与试件接触瞬间的初始冲击速度，在本次低速冲击实验中，设定初始冲击速度为7 m/s。

由于试件在冲击实验中的变形过程极其短暂，所以需要配备高速摄像仪，用来记录和观察实验件在冲击载荷作用下的变形过程，了解实验件的变形模式和能量吸收机理。

3.3 实验结果

图9(a)与图9(b)分别为预折纹管的实验与数值载荷-位移曲线对比图和能量-位移曲线对比图。从图9(a)中可以发现，通过有限元模拟得到的预折纹管的载荷位移曲线与通过实验得到的载荷位移曲线的变化趋势基本一致，波峰和波谷的数量、位置以及所对应的载荷大小相差较小，其中，在曲线的波峰与波谷时刻所对应的实验件变形形状与有限元模型的变形形状也非常相似；从图9(b)中可以发现，数值结果和实验结果的能量-位移载荷曲线在位移小于35 mm时基本贴合在一起，位移大于35 mm时误差也非常小，能量值的最大误差出现在位移为60 mm处，误差为7.7%。

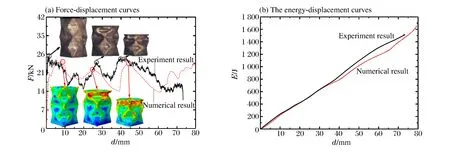
图9 预折纹管的实验与数值对比Fig.9 Comparison between the falling weight impact test result and the numerical simulation result

图10 预折纹管变形前后对比Fig.10 Comparison of the pre-folded tube before and after deformation

预折纹管的实验与数值对比结果验证了数值计算的正确性，为了进一步证明折纹的引入对预折纹管变形模式的影响，图10给出预折纹管在变形前和变形后的对比，左图中塑性铰线交点(图中圆圈标记点)相距较远，而随着塑性铰线的移动，铰线交点也随之不断靠近，可以发现，塑性铰线的交点即为预折纹管引入折角的顶点，因此图中的塑性铰线交点位置的变化再次证明了折角引导预折纹管发生了新的大变形模式。因此可以预见，预折纹管与普通方管的实验对比结果也将与数值对比结果相似。

图11(a)和图11(b)分别为预折纹管和普通方管的载荷位移曲线和能量位移曲线对比图。从图11(a)中可以发现，峰值载荷从普通方管的88.86 kN降低到预折纹管的27.77 kN，降低了68.7%，而且预折纹管的载荷曲线比普通方管的载荷曲线要平稳很多，预折纹管的载荷曲线没有明显的下降趋势，而普通方管的载荷曲线则下降比较明显；从图11(b)中可以发现，在相同加载位移处(70 mm)的平均载荷也从普通方管的15.41 kN提高到了预折纹管的20.83 kN，提高了35.2%；压缩力效率从普通方管的0.17提高到了预折纹管的0.75，提高了314.2%。

图11 预折纹管和普通方管实验结果对比Fig.11 Comparison between the pre-folded tube and the ordinary square tube

4 讨 论

4.1 误差分析

实验结果与有限元分析结果的主要误差来自于实验与有限元的各种条件的不一致性，包括以下几个方面。

(1) 实验试件与有限元模型的几何性质存在不一致性：预折纹管与普通方管的试验件有2条焊缝，而有限元模型没有焊缝；为了使普通方管发生对称变形，有限元模型加入了引导槽，而实验试件则没有，所以加入初始缺陷的有限元模型的峰值载荷为45.99 kN，而实验试件的峰值载荷为88.86 kN。

(2) 实验与有限元模拟的边界条件存在不一致性：实验试件的底边与落锤式冲击实验机的冲击台上表面为自由接触，而有限元模拟过程中，有限元模型的底边与模拟冲击台的下刚性板为固定约束。

(3) 实验与有限元模拟的加载条件存在不一致性：落锤实验前通过操作系统赋予落锤的初始速度通过公式v=(2gh′)0.5换算成落锤与实验试件的垂直高度h′，而没有考虑落锤与引导落锤下落的钢杆的摩擦，所以实验中落锤的初始速度相较有限元计算中要略小。

4.2 总 结

本文中研究一种新型预折纹管，即在普通方管的管壁上引入折角，预想这种折角的引入可以提高其吸能效率。为了验证这种理论，从数值和实验2个方面进行研究，基于数值结果分析可以得到，通过引入折角可以使预折纹管在轴向冲击载荷作用下发生预定的变形模式，而这种变形模式导致了能量效率的提高。同时文章基于折角的几何特性对吸能效率提高的原因进行剖析，发现折角的引入使方管原本垂直于横截面的棱边和侧面都发生了一定的倾斜，而这种倾斜削减了普通方管的轴向刚度，降低了普通方管的峰值载荷；另外折角的引入还使普通方管的移动塑性铰线数量增加了一倍，导致预折纹管管壁上塑性区的面积较普通方管的扩大了很多，也就增加了能量的吸收。为了证明这种分析的正确性，进行了实验验证，实验结果证明了数值结果的准确性，也证明了提出的关于预折纹管吸能效率提高的理论的正确性。实验和数值结果的关键吸能性能指标如表1所示，其中：S2为方差。表1中，S2和Fm是位移为70 mm时的计算值。

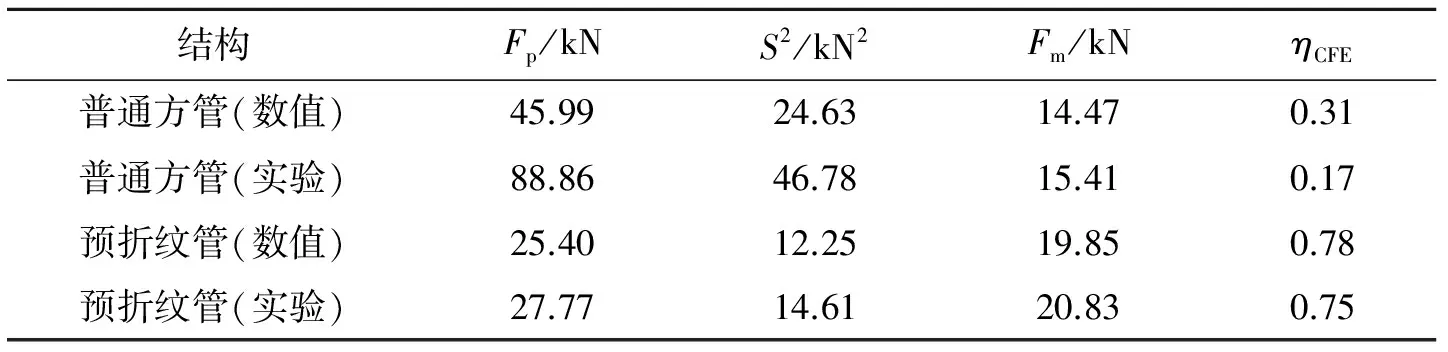
表1 普通方管和预折纹管的比较结果

针对表中的数据可以总结如下。首先，通过有限元模拟结果和实验结果中峰值载荷和平均载荷的对比可以发现，除了普通方管的峰值载荷有较大误差(48.2%)外，预折纹管的峰值载荷误差为8.5%，普通方管的平均载荷误差为6%，预折纹管的平均载荷误差为4.7%，而普通方管峰值载荷误差原因在4.1节中已有解释，所以本文中的有限元模拟结果可信度较高；其次，通过预折纹管与普通方管的峰值载荷对比可以发现，预折纹管的峰值载荷在有限元计算结果中较普通方管的峰值载荷减小了44.8%，而在实验中测得峰值载荷减小了68.7%，无论是有限元结果还是实验结果都验证了在预折纹管管壁上引入的折角能够减少初始峰值；再次，通过预折纹管与普通方管的载荷方差对比可以发现，预折纹管的载荷方差在有限元计算结果中较普通方管的载荷方差减小了50.3%，而在实验中测得载荷方差减小了68.8%，无论是有限元结果还是实验结果都验证了在预折纹管管壁上引入的折角能够减少载荷方差，即增加了载荷的平稳性；另外，通过预折纹管与普通方管吸收的平均载荷对比可以发现，预折纹管吸收的平均载荷在有限元计算结果中较普通方管吸收的平均载荷增加了37.2%，而在实验中测得的平均载荷增加了35.2%，无论是有限元结果还是实验结果都验证了在预折纹管管壁上引入的折角能够增加平均载荷；最后，通过预折纹管与普通方管的压缩力效率对比可以发现，预折纹管的压缩力效率在有限元计算结果中较普通方管的压缩力效率增加了151.6%，而在实验中计算得的压缩力效率增加了314.2%，无论是有限元结果还是实验结果都验证了在预折纹管管壁上引入的折角能够极大地增加吸能效率。

[1] Olabi A G, Morrisa E, Hashmi M S J. Metallic tube type energy absorbers: A synopsis[J]. Thin-walled Structures, 2006,45(7/8):706-726.

[2] Stein E, Borst R, Huges T J R. Encyclopedia of computational mechanics[M]. New York, USA: John Wiley & Sons, 2004:25-46.

[3] Zhong Z H, Zhang W G, Cao L B. Automotive crash safety technology[M]. Beijing: China Machine Press, 2003:112-152.

[4] Airoldi A, Janszen G. A design solution for a crashworthy landing gear with a new triggering mechanism for the plastic collapse of metallic tubes[J]. Aerospace Science and Technology, 2005,9(5):445-455.

[5] Tyrell D, Jacobsen K, Martinez E, et al. A train-to-train impact test of crash energy management passenger rail equipment: Structural results[C]∥Proceedings of IMECE2006. Chicargo, Illiois, USA, 2006.

[6] Hu Z Q, Cui W C. Review of the researches on the ship collision mechanisms and the structural designs against collision[J]. Journal of Ship Mechanics, 2005,9(2):131-142.

[7] 杨嘉陵,吴卫华,刘旭红,等.直升机整体机坠毁设计的简化力学模型[J].机械工程学报,2003,39(12):109-113. Yang Jia-ling, Wu Wei-hua, Liu Xu-hong, et al. The simplified mechanics model of helicopter design when crashed[J]. Chinese Journal of Mechanical Engineering, 2003,39(12):109-113.

[8] 李玉龙,石霄鹏.民用飞机鸟撞研究现状[J].航空学报,2012,33(2):189-198. Li Yu-long, Shi Xiao-peng. Research status of bird strike civilian aircraft[J].Acta Aeronautica et Astronautica Sinica, 2012,33(2):189-198.

[9] Zhang L L, Gao F. Researches development on the crashworthiness about metal: thin-walled structures[J]. Metal Forming, 2006,32(5):76-78.

[10] Lu G X, Yu T X. Energy absorption of structures and materials[M]. Woodhead, Florida, USA: CRC Press, 2003:12-18.

[11] Du X W, Song H W. Impact dynamics and crashworthiness design of cylindrical shell[M]. Beijing: Science Press, 2004:16-30.

[12] Yu T X. Impact energy absorbing devices based upon the plastic deformation of metallic elements[J]. Advances in Mechanics, 1986,16(1):28-39.

[13] Yuen S C K, Nurick G N. The energy-absorbing characteristics of tubular structures with geometric and material modifications: an overview[J]. Applied Mechanics Review, 2008,62(2):0208021-02080215.

[14] Abramowicz W. Thin-walled structures as impact energy absorbers[J]. Thin-walled Structures, 2003,41(2/3):91-107. DOI: 10.1016/S0263-8231(02)00082-4.

[15] Liu Y C. Crashworthiness design of multi-corner thin-walled columns[J].Thin-walled Structures, 2008,46(12):1329-1337. DOI:10.1016/j.tws.2008.04.003.

[16] Yamazaki K, Han J.Maximization of the crushing energy absorption of cylindrical shells[J]. Advances in Engineering Software, 2000,31(6):25-434. DOI:10.1016/S0965-9978(00)00004-1.

[17] Gibson L J, Ashby M F. Cellular solids[M]. Cambridge, UK: Cambridge University Press, 1999,51:48-57.

[18] Song J, Chen Y, Lu G. Axial crushing of thin-walled structures with origami patterns[J]. Thin-Walled Structures, 2012,54:65-71.

[19] Ma J, You Z. Energy absorption of thin-walled square tubes with a prefolded origami pattern: Part Ⅰ: geometry and numerical simulation[J]. Journal of Applied Mechanics, 81(1):011003-1-011003-11.

[20] Ma J, You Z. Energy absorption of thin-walled beams with a pre-folded origami pattern[J]. Thin-Walled Structures, 2013,73(1):198-206.

[21] Wierzbicki T, Abramowicz W. On the crushing mechanics of thin-walled structures[J]. Journal of applied Mechanics, 1983,50(4a):727-734. DOI: 10.1115/1.3167137.

[22] Hsu S S, Jones N. Quasi-static and dynamic axial crushing of thin-walled circular stainless steel, mild steel and aluminum alloy tubes[J]. International Journal of Crashworthiness, 2010,9(2):195-217.

[23] SIMULIA. ABAQUS Analysis User’s Manual[M]. Documentation Version 6.10. Providence, RI, USA: Dassault Systems Simulia Corp, 2007:32.5.2.1-32.5.2.6.

[24] Meng Q, Al-Hassani S T S, Soden P D.Axial crushing of square tubes[J].International Journal of Mechanical Sciences, 1983,25(9/10):747-773.

(责任编辑 王小飞)

Energy absorption of pre-folded origami under low speed impact

Wang Bo1,2, Zhou Cai-hua1,2, You Zhong3

(1.DepartmentofEngineeringMechanics,DalianUniversityofTechnology,Dalian116024,Liaoning,China; 2.StateKayLaboratoryofStructuralAnalysisforIndustrialEquipment,DalianUniversityofTechnology,Dalian116024,Liaoning,China; 3.DepartmentofEngineeringScience,UniversityofOxford,OxfordOX13PJ,UK)

A new type of creased square tube specifically designed with some folded lobes added at the wall of ordinary square tube is studied inorder not only to reduce the initial loading, but also to enhance the effective plastic area distortion which leads to a higher energy absorption efficiency. The numerical results based on the FEM package ABAQUS /EXPLICIT verify that the pre-folds could lead the pre-folded origami to the expected large deformation mode under low speed impact, which effectively reduce the peak load and also improve the average load of load-displacement curve compared with ordinary square tubes. The load-displacement curve obtained by FEM is identical to the results of low droped hammer test, which verifies the credibility of the numerical results as well as the high energy absorption characteristics of the tube.

solid mechanics; energy absorption; low droped hammer test; thin-walled structure; crashworthiness design

10.11883/1001-1455(2015)04-0473-09

2013-11-29；

2014-03-05

国家自然科学基金项目(11128205,11372062)；国家重点基础研究发展计划(973计划)项目(2014CB049000)；高等学校学科创新引智计划项目(B14013)；辽宁省高等学校优秀人才支持计划项目(LJQ2013005)

王 博(1978- )，男，博士，教授，wangbo@dlut.edu.cn。

O381 国标学科代码： 13035

A