大孔径静态破碎膨胀压力特性及布孔参数分析

姜 楠 ,徐全军 ,龙 源 ,廖 瑜 ,林 卫

(1.解放军理工大学野战工程学院，江苏 南京 210007； 2.南京市城建集团，江苏 南京 210002)



大孔径静态破碎膨胀压力特性及布孔参数分析

姜 楠1,徐全军1,龙 源1,廖 瑜1,林 卫2

(1.解放军理工大学野战工程学院，江苏 南京 210007； 2.南京市城建集团，江苏 南京 210002)

大孔径静态破碎与传统静态破碎有着显著的不同。利用电测法测量了直径40和100 mm钢管中的破碎剂膨胀压力和温度，对比分析了两种工况下的不同现象。实验表明，孔径的增加能够提高膨胀压力，加快反应速度。基于实验的数据，利用有限元方法计算了静态破碎时钻孔周围岩石介质中的应力分布。基于实验数据和有限元数值计算结果，使用数据拟合方法对静态破碎时岩石中的应力分布弹性模型进行修正，得到了应力分布方程。利用该方程推导的布孔参数计算公式，适合运用于实际工程之中。

爆炸力学；静态破碎；有限元方法；大孔径；数据拟合；应力分布

开矿采矿以及城市建设中，传统的爆破法施工常受到限制，尤其在部分爆破敏感区域，炸药爆破引起的地震波、噪音等会对周围环境造成很大影响。基于静态破碎剂与水反应产生膨胀力原理的静态破碎技术可较好地解决爆破敏感区域的破岩问题。静态破碎技术一出现，其实验和理论研究及工程应用就从各角度展开[1-3]，但仍存在着诸多局限[4]，如膨胀力弱、反应时间长、容易喷孔等。

为拓展静态破碎的使用范围，使之能用于大规模土岩破碎，人们开始研究大孔径静态破碎技术[4]。利用机械堵孔器和扩孔钻技术较好地解决了大孔径静态破碎中的喷孔现象，使大孔径爆破技术在实际工程中有了初步应用[5]。但针对大孔径静态破碎的基础研究目前尚未开展，需进一步针对大孔径静态破碎的特点进行研究。现有的静态破碎的基础研究基本都基于传统的小孔径(小于50 mm)的情况。游宝坤[6]系统地阐述了静态破碎技术的原理和应用方法以及工程实例。王玉杰[7]使用X射线衍射物相定量分析方法，建立了相应的静态破碎剂水化反应动力学方程及其参数。S.Arshadnejad等[8]修正了静态破碎空孔距离模型与应力分布方程，并使用有限元数值计算模拟了静态破碎中的裂纹发展过程，并与混凝土实验相对比。J.A.Gambatese[9]采用间隔装药方式进行静态破碎，并研究了不同布孔方式的混凝土裂缝形成规律。D.F.Laefer等[10]研究了不同的环境温度下，不同的约束条件下，不同种类静态破碎剂对周围介质裂纹生成的影响，分析了初始断裂时间与外部因素的关系。

本文中针对大孔径静态破碎进行实验和理论研究，并与小孔径静态破碎对比。对静态破碎时的岩石应力分布的弹性模型进行修正，建立一种比较简单而又准确的应力分布模型和布孔参数计算公式，使之能够运用于实际工程当中。

1 静态破碎膨胀压力测试实验

1.1 实验原理与装置

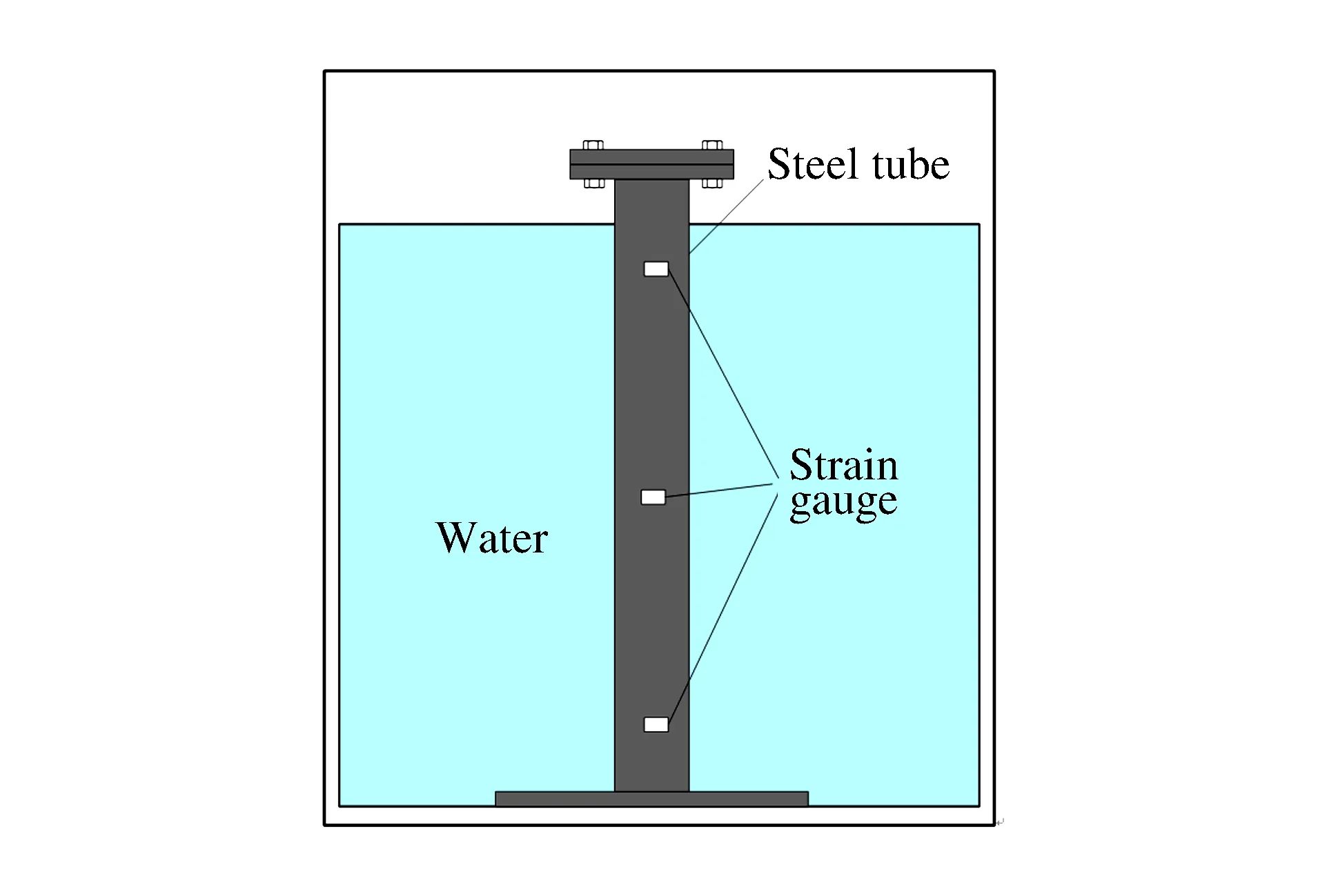
图1 实验装置示意图Fig.1 Experiment devices

为了定量研究大孔径静态破碎过程中破碎剂作用在孔壁上的膨胀压力情况，进行了破碎剂的膨胀压力测试实验。实验采用电阻应变测量法来测定静态破碎剂的膨胀压力大小。实验分别在直径40和100 mm的钢管中进行，实验室环境温度为10 ℃，为防止反应放热过高，将实验装置放入水中，水温与环境温度相同，实验装置如图1所示。

通过贴在钢管外的电阻应变片来测量钢管的环向应变，通过弹性力学中薄壁筒理论来计算钢管所受的膨胀压力，通过贴在钢管上部表面(水面以上)的热电偶来测量破碎剂反应时的反应温度。实验所用电阻应变片为高温电阻应变片，并与热电偶一起接入动态数据采集系统DH5922。

实验仅比较环向应变，将测得的应变值按下式换算为破碎剂的径向膨胀压力[11]：

(1)

式中：p为膨胀压力；钢管弹性模量E=206 GPa；K为钢管外径与内径之比；εθ为环向应变；钢管材料泊松比ν=0.3。

1.2 实验数据分析

仅取钢管中部应变片的测量值进行比较。

(1) 直径40 mm钢管中破碎剂膨胀压力及反应温度。

图2为直径40 mm钢管中破碎剂膨胀压力时程曲线，破碎剂膨胀压力在20 h内较快地上升为15 MPa，之后缓慢上升，在100 h时升至30 MPa。温度时程曲线表明，破碎剂在水灰混合之后40 min后开始水化反应，80 min时温度达到最高值35 ℃，此时水化反应基本结束，破碎剂温度逐渐降回室温。

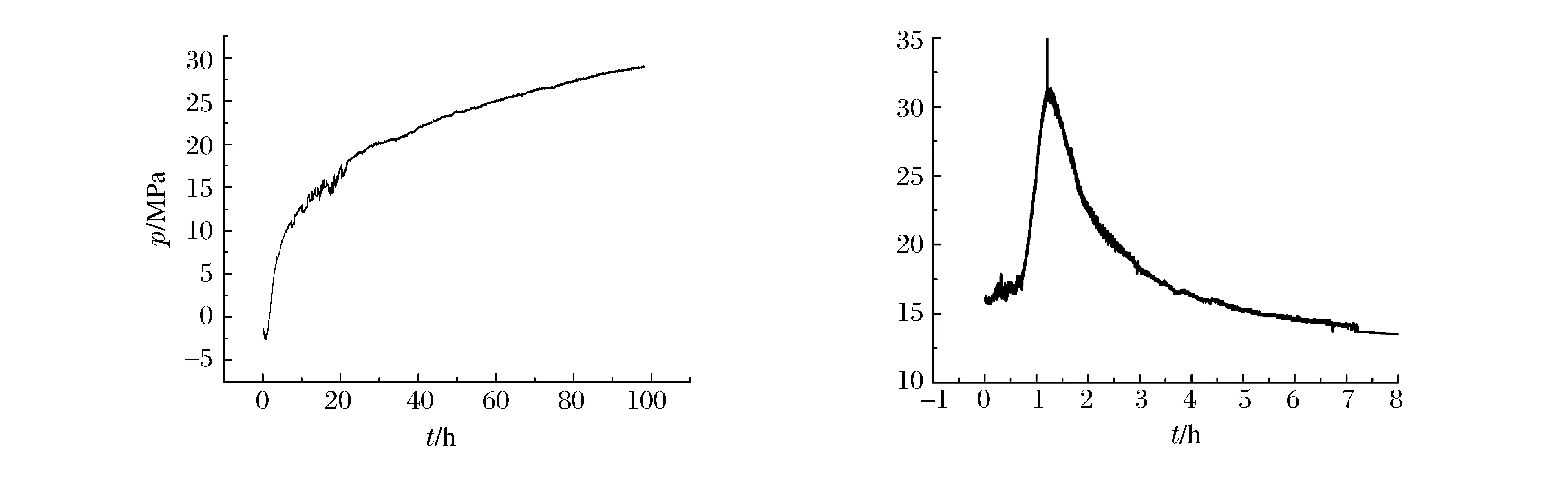
图2 膨胀压与温度时程曲线(∅40 mm)Fig.2 SCA’s expasive pressure and temperature(∅40 mm)

(2) 直径100 mm钢管中破碎剂膨胀压力及反应温度。

图3为直径100 mm钢管中破碎剂膨胀压力时程曲线，破碎剂膨胀压力在60 min左右很快地上升为200 MPa，之后迅速下降至97 MPa并保持稳定。温度时程曲线表明，破碎剂在水灰混合之后40 min左右开始水化反应，而后迅速温度达到最高值235 ℃，此时水化反应基本结束，温度逐渐降回室温。

实验各数据列表对比见表1，其中：d为孔径，η为水灰比，ps为膨胀压力稳定值，Tm为反应温度峰值，t0为破碎机反应起始时间。

表1 钢管实验数据

图3 膨胀压与温度时程曲线(∅100 mm)Fig.3 SCA’s expasive pressure and temperature(∅100 mm)

对比直径40和100 mm钢管内的破碎剂膨胀压力时程曲线和温度时程曲线，可以看出，2种情况的膨胀过程有着明显的不同。

小直径情况下，破碎剂浆体温度最高只上升了15 ℃左右，温度变化较为缓慢，表征其反应过程也较为平缓，从而整个膨胀过程也较为平缓，甚至100 h后还在缓慢膨胀，其处于一个缓慢结晶膨胀过程。

大直径情况下，破碎剂质量大，比表面积小，水化反应热的产生大于热量的传递与消耗，热量积累并进一步催化反应。60 min后，温度很快地超过100 ℃，破碎剂浆体中的水分迅速气化，短时间内管内压力升高，产生一个压力突跃的过程。随着反应的结束和水蒸气的泄漏，管内压力迅速降低。由于水分的气化和高温，破碎剂浆体迅速固化达到稳定膨胀压力值，该值比小直径情况有明显增大。

2 静态破碎的岩石应力模型

2.1 岩石应力分布模型

岩土中大孔径静态破碎问题可使用弹塑性力学中的厚壁圆筒理论进行研究。在厚壁圆筒理论中[12]，假设存在一个厚壁圆筒，其内半径设为a，外半径设为b，并设其内壁与外壁分别受到均匀分布的压力p1和p2，径向拉应力σr和切向拉应力σθ表达式如下：

(2)

式中：r为距炮孔的距离。

圆筒只受内壁上破碎剂膨胀压力p1的作用，外壁的压力p2=0，所以，此时应力为：

(3)

在无限介质中，可以认为b→∞，式(7)可以写作：

(4)

式(4)就是静态破碎破碎剂膨胀压力在周围介质产生的压力分布弹性解。由于实际孔壁周围并非完全弹性区，需对弹性解进行修正，下面利用有限元方法进行数值计算，并以此修正弹性解。

2.2 有限元数值计算与拟合修正方程

静态破碎破碎剂的膨胀压力与其所在介质的约束度有关系，外界约束不同，破碎剂产生的膨胀压力有所不同。但是由约束度实验可知[13]，破碎剂在钢管中和在混凝土、岩石中的所受的约束度差别不大，所以产生的膨胀压力也基本相同。本节中利用钢管测压实验中获得的数据的进行计算。

根据第一节中的膨胀压测试实验所测得的数据，进行有限元数值计算，对比研究静态破碎破碎剂在大小孔径中对岩石产生的应力分布情况，以此来确定岩石破碎时大孔径静态破碎的孔网参数。将问题简化为二维问题，分析在二维条件下的应力分布。将破碎剂的膨胀压力简化为沿孔壁法线方向的固定压力载荷，并假设岩体是各向同性的，设弹性模量E=20 GPa，ν=0.2，并使用摩尔-库伦强度准则进行计算，内摩擦角为35°，内聚力为12 MPa。其中一个模型的部分网格图和应力云图如图4所示。

图4 模型网格及应力云图Fig.4 Model mesh and stress counter

为得到一个相对简单的方程，将式(4)写作：

(5)

利用有限元计算结果对弹性解进行数据拟合，由于应力分布在10倍孔径之外远远小于一般介质的屈服极限，故在10倍孔径的范围内求解A和B。

(1) 破碎剂在∅40 mm孔中对岩石的作用。

炮孔孔径为40 mm，孔壁压力为30 MPa，应力与距离关系如图5所示(FE Data)。通过数据拟合得到r<10a时的应力分布修正函数为:

(6)

式中：σr和σθ单位为MPa，p1=30 MPa，a=0.02 m。该拟合函数表征相关度的决定系数为0.999 11和0.996 4，函数曲线如图5所示(Fitted curve)。

图5 应力分布曲线(∅40 mm)Fig.5 Stress distribution curve (∅40 mm)

(2)破碎剂在∅100 mm孔中对岩石的作用。

岩石中的炮孔孔径为100 mm，孔壁压力为97 MPa，应力与距离关系如图6所示(FE Data)，r<10a时的应力分布修正函数为：

(7)

式中：σr和σθ单位为MPa，p1=97 MPa，a=0.05 m。该拟合函数表征相关度的决定系数为0.999 54和0.999 71，函数曲线如图6所示(Fitted curve)。

图6 应力分布曲线(∅100 mm)Fig.6 Stress distribution curve (∅100 mm)

由数据拟合求得的应力分布修正方程(式(6)～(7))与有限元数值计算结果拟合度很高，表征相关度决定系数的值十分接近为1，表明这些方程在在r<10a的条件下可以较好的描述应力分布，适合用以计算抗拉强度相对较大(一般要大于3 MPa)的岩石中静态破碎的最小抵抗线以及最大孔间距等布孔参数。而且，由于应力分布与膨胀压以及炮孔孔径平方的乘积呈正比，所以在相同的条件下，具有更大膨胀压力和炮孔直径的大孔径静态破碎能够产生更大的应力分布范围，从而大大提高破碎效率。

3 大孔径静态破碎的参数分析

由上一节中的理论分析和数值计算，得到了静态破碎的应力分布函数，其一般形式为：

(8)

岩石介质中，其抗拉强度远小于抗压强度，所以本节用岩石的单轴抗拉屈服极限来表示相应的破坏屈服条件，使用静态破碎的拉应力分布函数对岩石的破坏进行分析。

当静态破碎存在自由面时，其最小抵抗线的长度可利用式(8)来确定。此时可将最小抵抗线长度H看作厚壁圆筒的外径，即H=b，于是在自由面边界上的拉应力为：

(9)

当该拉应力大于岩石介质抗拉强度σs时，岩石会产生拉伸破坏，形成裂纹，即：

(10)

所以最小抵抗线为：

(11)

利用静态破碎在无限介质中的拉应力分布函数(式(5))，可以推出最大孔间距L计算公式。两孔间的拉应力最大位置位于两孔中心连线上，两个连续孔中的静态破碎破碎剂所产生的拉应力之和大于岩石抗拉强度时，即可产生破坏，形成裂纹，即：

(12)

得最大孔间距为：

(13)

将上一节中所计算出的参数B的值带入式(13)，可以得到一个比较简单，在实际工程中非常容易计算的静态破碎布孔参数公式。

4 结 论

大孔径静态破碎与已有的小孔径静态破碎相比，其特性有显著地不同。其自身膨胀力较大，并且膨胀作用时，破碎应力分布范围也更广。本文采用有限元数值计算方法以及数据拟合方法，结合实验测试所得数据，对不同孔径大小的静态破碎岩石应力分布模型进行修正，得到以下结论。

(1)静态破碎的膨胀压时程曲线与温度时程曲线显示，在相同条件下，直径100 mm钢管中的破碎剂膨胀压力为97 MPa，最高温度为235 ℃；直径40 mm钢管中的破碎剂膨胀压力为30 MPa，最高温度为35 ℃。直径100 mm钢管中的破碎剂反应速度比40 mm的快。实验表明，大孔径静态破碎具有膨胀压力大，温度高，反应快等特点。

(2)使用实验数据对100 mm孔径与40 mm孔径下的岩石受力情况进行有限元数值计算，计算得到了两种单孔情况下的岩石应力分布云图与应力分布曲线。利用有限元数值计算结果拟合修正的弹性模型和分布方程能够准确地描述静态破碎时岩石的应力分布情况。

(3)由分布方程推导的静态破碎的最小抵抗线公式和孔间距公式等孔网参数计算方程形式简单，结果准确。

[1] 孙立新.静态破碎剂的研制及应用[D].西安:西安建筑科技大学,2005.

[2] 李星.预留缝PVC管混凝土试块静态破碎试验研究[D].合肥:安徽理工大学,2012.

[3] 曹鑫.静态破裂剂膨胀机理的研究[D].武汉:武汉理工大学,2007.

[4] 温尊礼,徐全军,姜楠,等.新型大孔径静态破碎技术的试验研究[J].探矿工程(岩土钻掘工程),2013,40(5):72-74. Wen Zun-li, Xu Quan-jun, Jiang Nan, et al. Experimental study on a new technology of static blasting in large diameter borehole[J]. Exploration Engineering (Rock & Soil Drilling and Tunneling), 2013,40(5):72-74.

[5] Xu Q J, Jiang N, Long Y, et al. Study of a new large scale borehole soundless cracking technology[C]∥Proceedings of the 23rd World Mining Congress, Montreal, Canada, 2013.

[6] 游宝坤.静态爆破技术[M].北京:中国建筑工业出版社,2008:1-4.

[7] 王玉杰.静态破裂技术及机理研究[D].湖北:武汉理工大学,2009.

[8] Arshadnejad S, Goshtasbi K, Aghazadeh J. A model to determine hole spacing in the rock fracture process by non-explosive expansion material[J]. International Journal of Minerals, Metallurgy and Materials, 2011,18(5):509-513.

[9] Gambatese J A. Controlled concrete demolition using expansive cracking agents[J]. Journal of Construction Engineering and Management, 2003,129(1):98-104.

[10] Laefer D F, Ambrozevitch-Cooper N. Expansive fracture agent behaviour for concrete cracking[J]. Magazine of Concrete Research, 2010,62(6):443-452.

[11] 中华人民共和国国家发展和改革委员会.JC506-2008 无声破碎剂[S].北京:中国建材工业出版社,2008.

[12] 徐秉业,刘信声.应用弹塑性力学[M].北京:清华大学出版社,1995.

[13] 邹俊兴.约束度对静力破碎剂压力的影响[J].爆破,1991,8(4):17-20.

(责任编辑 王小飞)

Expansive pressure characteristic and borehole parameter analysis on large scale borehole soundless cracking

Jiang Nan1, Xu Quan-jun1, Long Yuan1, Liao Yu1, Lin Wei2

(1.CollegeofFieldEngineering,PLAUniversityofScienceandTechnology,Nanjing210007,Jiangsu,China; 2.NanjingUrbanConstructionInvestmentHolding(Group)LimitedCorporation,Nanjing210002,Jiangsu,China)

Large scale borehole soundless cracking is significantly different from traditional soundless cracking. Experiments were made to measure the expansive pressure of the soundless cracking agent (SCA) working in the boreholes of ∅40 mm and ∅100 mm. The different phenomenon between two sizes of cracking was compared and analyzed to show that the increase of borehole diameter could increase the expansive pressure and speed up the reaction. Based on the experimental data, finite element analysis was utilized to study the stress concentration and stress distribution around the borehole during the cracking process. Using the experimental data and the results of the finite element method, the elastic model of rock stress distribution was modified, and the stress distribution equations were proposed. The formulas of borehole arrangement parameters deduced by those equations are suitable for the actual engineering.

mechanics of explosion; soundless cracking; finite element method; large scale borehole; data fitting; stress distribution

10.11883/1001-1455(2015)04-0467-06

2013-12-23；

2014-03-06

姜 楠(1988- )，男，博士研究生，csmjiangnan@qq.com。

O383 国标学科代码： 13035

A