改进布谷鸟算法优化混合核LSSVM 的卷烟销售量预测
2015-04-16周建友张凯威
周建友,张凯威
ZHOU Jianyou1,ZHANG Kanwei2
1.遵义市烟草公司 道真县分公司,贵州 遵义563500
2.贵州大学 计算机科学与信息学院,贵阳477004
1.Daozhen Branch,Zunyi Tobacco Company,Zunyi,Guizhou 563500,China
2.College of Computer Science and Information,Guizhou University,Guiyang 477004,China
1 引言
卷烟销售是卷烟行业管理中最为关键的内容,卷烟销售的预测可以为卷烟生产、运输、配送提供指导,因此设计高精度的卷烟销售预测模型是卷烟管理领域中的重要研究课题[1]。
多年来,国内外大量学者对卷烟销售预测进行了大量的研究,并提出一些预测模型[2]。传统卷烟预测模型包括回归分析方法、时间序列法、灰色关联法和马尔可夫链等,它们假设卷烟销售量是一种线性变化趋势,而实际上卷烟销售量受到经济、人口、市场波动和季节等多种因素综合影响,具有非线性、随机变化特点,因此,传统预测模型难以正确描述该变化趋势,卷烟销售的预测精度不理想[3]。随着非线性理论不断发展,出现了基于神经网络等非线性预测模型,并取得了比较好的预测效果,但其对学习样本的需求量大,而获得的卷烟销售量训练样本非常有限,因此预测结果有时出现过拟合现象[4-6]。最小二乘支持向量机(LSSVM)是一种专门研究小样本情况下的机器学习算法,一定程度上解决了神经网络过学习和欠学习以及局部最优解、维数灾难等问题,为解决小样本卷烟销售量预测提供了一种新的研究方法[7]。不同参数下的LSSVM 预测精度差别大,出现了基于粒子群优化算法、遗传算法、野草算法等LSSVM参数优化方法,但这些算法均存在各自的不足,因此选择合适的LSSVM参数是提高卷烟销售预测精度的关键[8-11]。Yang 和Deb 于2009 年提出模拟布谷鸟寻窝产卵行为的全局搜索方法—布谷鸟搜索(Cuckoo search,CS)算法,具有容易实现、参数设置少等优点,一些研究表明,CS算法的性能超过了遗传算法和粒子群优化算法[12-13]。
为了提高卷烟销售量预测精度,提出一种改进布谷鸟算法(MCS)优化混合核LSSVM 的卷烟销售量预测模型(MCS-LSSVM),并通过仿真实验测试了MCS-LSSVM的可行性和优越性。
2 布谷鸟优化混合核LSSVM 的卷烟销售量预测模型
2.1 LSSVM 基本原理
给定N个训练样本{(xi,yi),…,(xN,yN)},其中xi为n维的训练样本输入,yi为训练样本输出,LSSVM 算法的目标优化函数为:

式中,φ(·)为核空间映射函数;w为权矢量;ei为误差变量;b为偏置量;μ和γ为可调参数。
为求解函数的最小值,构造Lagrange函数:

式中,αi为拉格朗日乘子。
对式(1)求偏导可得:
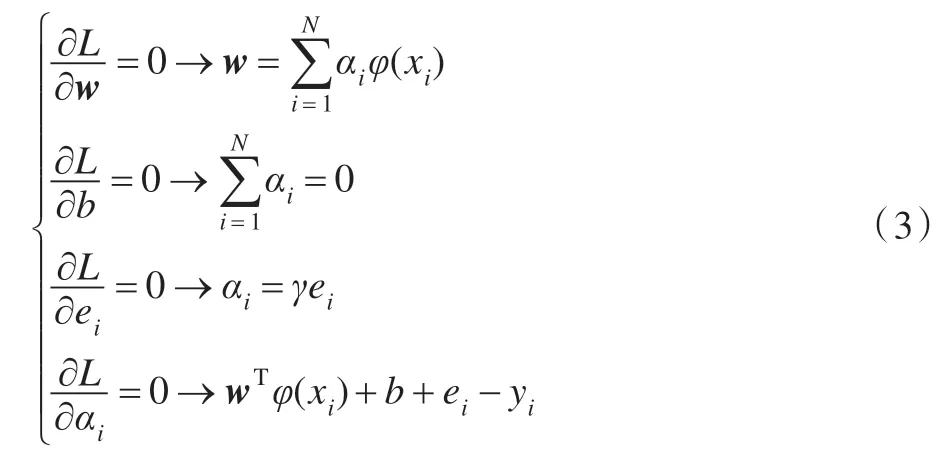
式中,i=1,2,…,N。
通过消去w和e,求解的优化问题转化为求解线性方程:
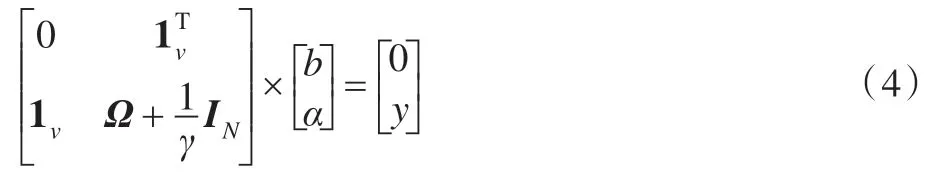
式中,y=[y1,y2,…,yN],1v=[1,1,…,1],α=[α1,α2,…,αN],Ω=φ(xi)Tφ(xi)=K(xi,xl)。
通过求解式(4)可得到α和b则用于函数估计的LSSVM 为:

式中,K(x,xi)为核函数。
2.2 混合核函数
不同核函数,构建不同的LSSVM 预测模型,当前核函数可分为全局和局部核函数,全局核函数的一个典型是多项式核函数,局部核函数的一个典型是RBF 核函数。为了提升LSSVM 的性能,得到学习能力和泛化能力都较强的核函数,本文将通过组合两种具有代表性的局部核函数(RBF 核函数)和全局核函数(多项式核函数)的映射特性,构造一种混合核函数,此混合核函数满足Mercer条件,其表达式为:
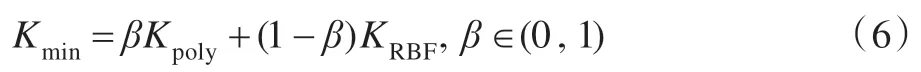
式中,Kpoly=[(x·xi)+1]2表示二次多项式核函数,KRBF=exp(-‖x-xi‖2/ 2σ2),σ>0 表示RBF 核函数,β是调整两种核函数对总的混合核函数的影响,即权系数。
2.3 改进的布谷鸟搜索算法(MCS)
在CS 算法中,一个鸟巢的卵表示一个候选解,一个布谷鸟的卵表示一个新的解,布谷鸟寻窝的路径和位置更新公式如下:


通过位置更新后,用随机数r∈[0, 1]与鸟窝的主人发现外来鸟的概率Pa对比,若r>Pa,则对进行随机改变,否则不变。
在基本CS 算法中,布谷鸟寻窝的路径和位置是随机的,以父代位置信息为参考进行更新。为了提高CS算法的性能,本文在布谷鸟寻窝的路径和位置更新公式(8)中引入惯性权重:
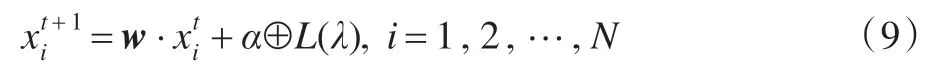
惯性权重的引入,可使CS 算法有扩展搜索空间的趋势,有能力搜索新的区域,实验表明,较大的惯性权重w有利于跳出局部最优,进行全局寻优;较小的w值有利于局部寻优,加速算法收敛。为了平衡算法的全局和局部搜索能力,惯性权重w的值应随着迭代次数的增加而递减。然而,CS 算法在实际搜索过程中是非线性的,惯性权重线性递减策略不能反映实际的优化搜索过程。因此,本文引入一种惯性权重非线性递减策略:

式中,iter为当前迭代次数。
2.4 MCS-LSSVM 的卷烟销售量预测步骤
(1)收集卷烟销售量历史数据,确定LSSVM 的输入与输出,生成LSSVM 的学习样本。
(2)根据经验确定β、γ、σ取值范围以及MCS 算法的相关参数值。
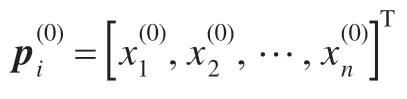
(4)保留上代最小误差Fmin对应的最优鸟巢位置。
(5)利用式(9)计算Levy Flight 步长大小,由Levy Flight对其他鸟巢进行更新,得到一组新的鸟巢位置,并计算它们的预测误差。

(8)找出步骤(7)最后找到pt中最优的一个鸟巢位置,并判断其最小误差Fmin是否满足卷烟销售量预测精度要求,如果满足,则停止搜索;反之,则返回步骤(4)继续寻优。
3 仿真实验
3.1 数据来源
在CPU P4 3.0 GMHz,RAM 2 GB,Windows 2000的PC 机上,采用VC++进行仿真实验。数据来自贵州某卷烟公司2012 年的某种卷烟销售数据,具体如图1 所示。选择前80 个样本作为训练集,其余40 个样本作为测试集。
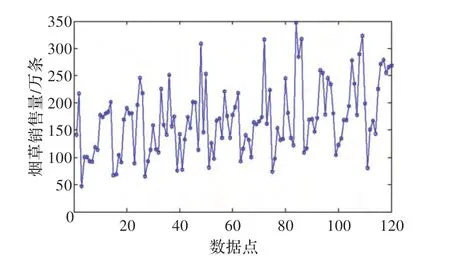
图1 卷烟历史销售数据
3.2 对比模型及性能评价标准
选择基本布谷鸟算法优化混合核LSSVM(CS-LSSVM)、改进谷鸟算法优化RBF 核的LSSVM(RBF-LSSVM)以及改进谷鸟算法优化BP 神经网络(MCS-BPNN)进行对比实验。单步预测模型主要考察预测点的精度,采用均方根误差RMSE和平均绝对百分误差MAPE作为模型的评价标准,它们定义如下:
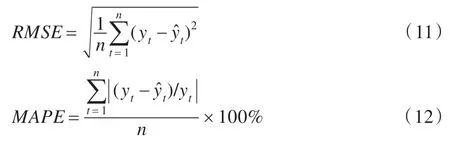
式中,yt表示实际值,表示预测值,n表示样本数。
3.3 构建LSSVM 学习样本
卷烟销售量具有后效性,当前时间的卷烟销售量与前一段时间卷烟销售量有关,需要通过确定最佳时延对LSSVM 学习样本进行构建。本文采用逐步增加时延数,并通过比较其预测精度来确定最佳时延数,具体化变化曲线如图2 所示。从图2 可知,卷烟销售量的最佳时延为5,即表示当前时刻的卷烟销售量与前5 个时间点的卷烟销售量相对应,从而形成LSSVM 的卷烟销售量学习样本。
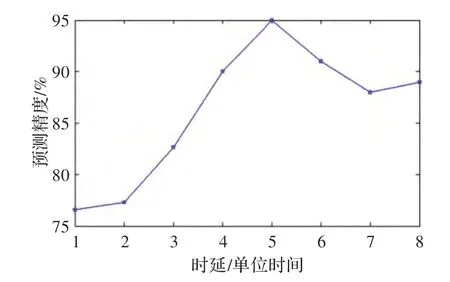
图2 确定卷烟销售量的最佳时延
3.4 结果与分析
3.4.1 单步预测性能分析
对重构后的卷烟销售量数据,选择最后40 个卷烟销售量数据作为测试集,其他数据作为训练集,利用MCS-LSSVM 建立卷烟销售量预测模型,MCS-LSSVM的预测结果与实际卷烟销售量如图3 所示,预测结果的误差变化曲线如图4 所示。对图3 和4 进行分析可知,MCS-LSSVM 的单步预测结果与实际输出相当吻合,具有较高的预测精度,具有良好的泛化推广性。
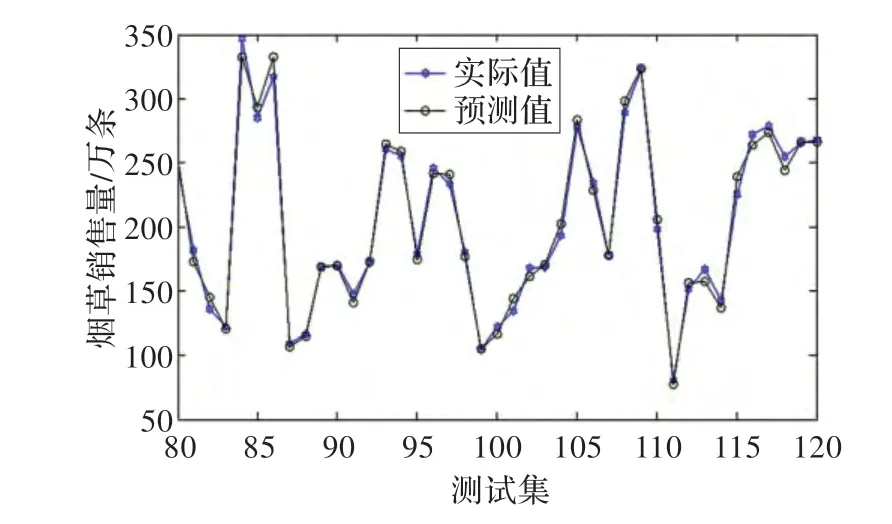
图3 单步预测结果与实际输出的变化曲线
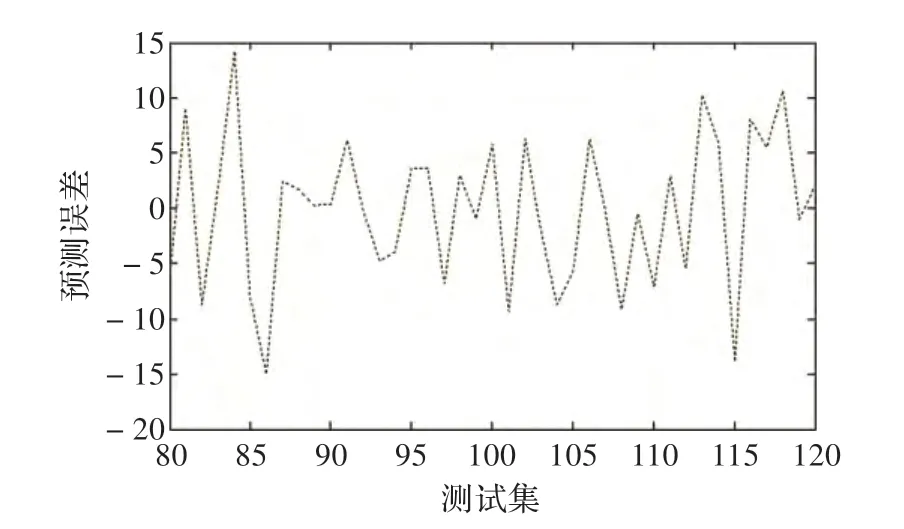
图4 卷烟销售量测试集预测结果的误差分布
各模型单步预测结果见表1。从表1 可知,与对比模型相比,MCS-LSSVM 的卷烟销售量预测结果更优,具有更好的优越性和稳健性。
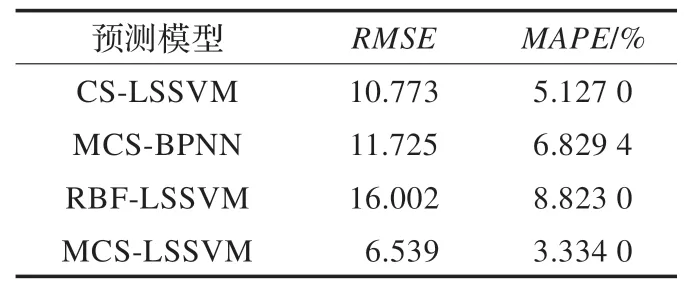
表1 不同模型的单步预测性能对比
3.4.2 提前多步预测性能分析
通常预测要求有较大的提前时间量,采用一步预测(即仅对下一个时间的卷烟销售量进行预测),既不能有效反映卷烟销售量变化趋势,也无法针对卷烟销售量对销售策略做出改变。因此,有必要将一步预测扩展到多步预测,于是采用多步预测模型对未来多个时刻的卷烟销售量进行预测,所有模型均采用迭代法的多步预测,即重复使用一步向前预测若干次,并把上一次的预测值视作系统输出真值,应用于下一次预测中。采用MCSLSSVM 构建卷烟销售量预测的多步预测模型,分别提前2 步、3 步预测,提前2 步预测结果和实际输出值如图5 所示。从图5 可以看出,MCS-LSSVM 模型对卷烟销售量测试集提前2 步预测输出与实际输出几乎相同,预测结果的预测误差变化曲线如图6 所示,预测误差控制在有效范围内,只能够在很小的数量级上才能区分,获得了较高的预测精度。
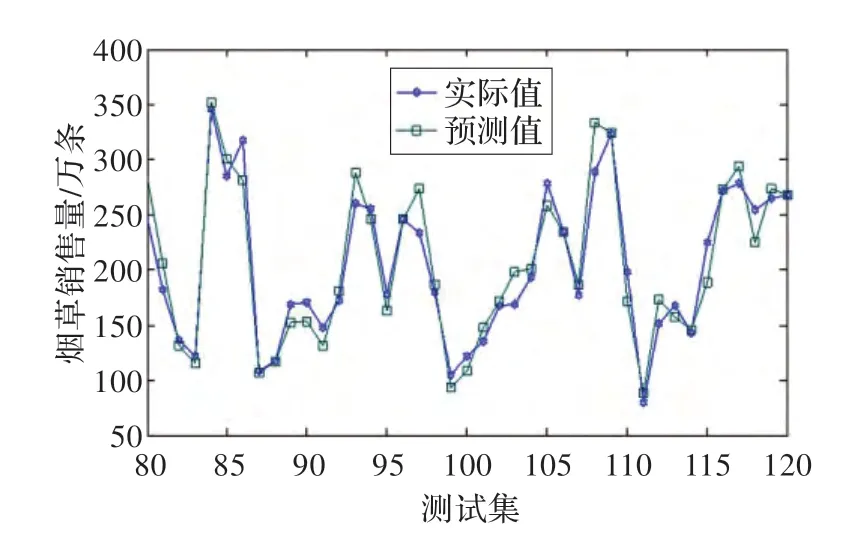
图5 提前2 步预测结果与实际输出
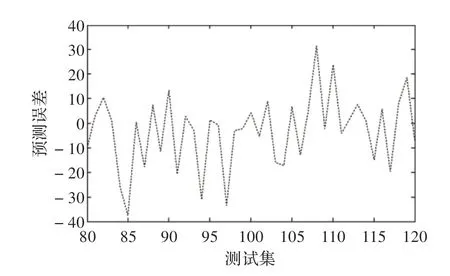
图6 提前2 步预测误差分布
MCS-LSSVM 提前3 步预测卷烟销售量结果和实际输出值如图7,各点预测误差分布如图8 所示。从图7 可以看出,MCS-LSSVM 对卷烟销售量测试集的提前3 步预测输出与实际输出符合得很好,因此,预测模型具有很好的推广性。
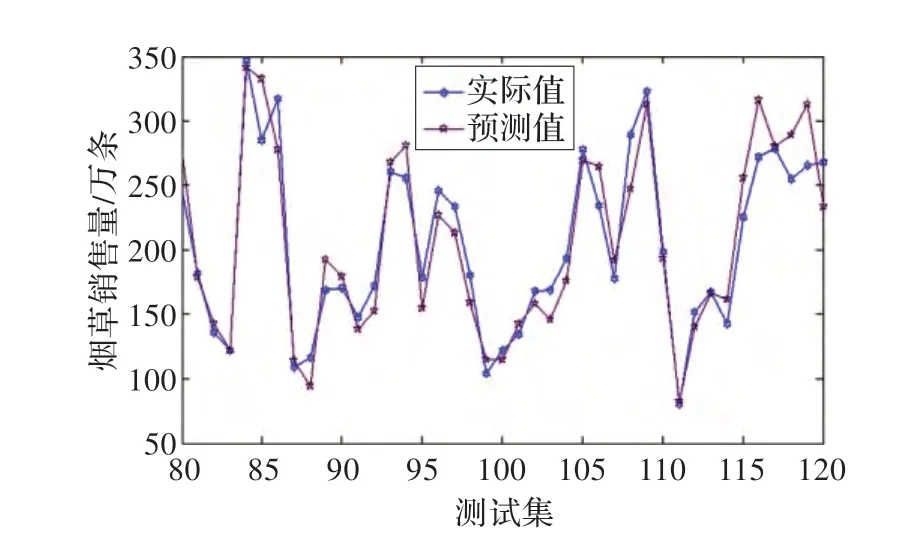
图7 提前3 步预测结果与实际输出
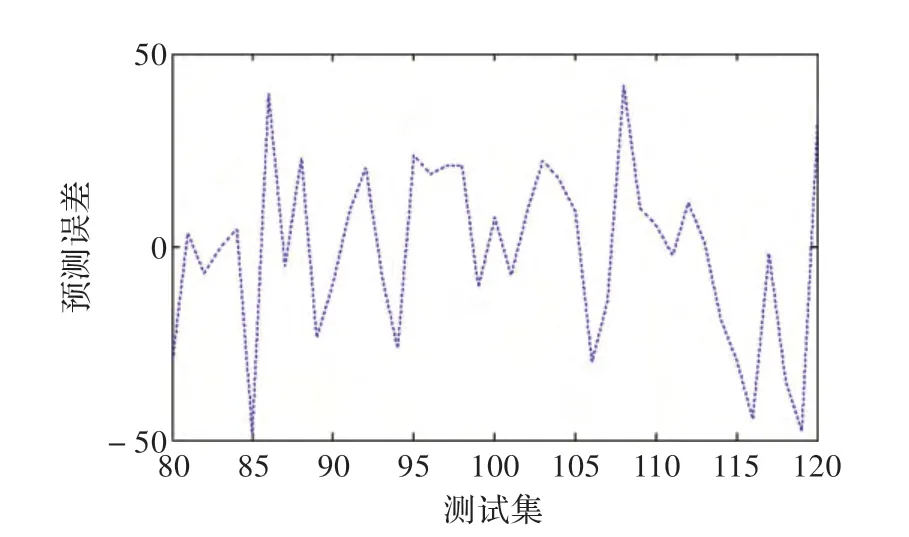
图8 提前3 步预测误差分布
不同卷烟销售量预测模型的预测性能对比见表2。对表2的结果进行分析可知,相对于对比模型,MCS-LSSVM具有预测性能高,预测结果更加准确、可靠等优点,是一种预测精度高的卷烟销售量预测模型。
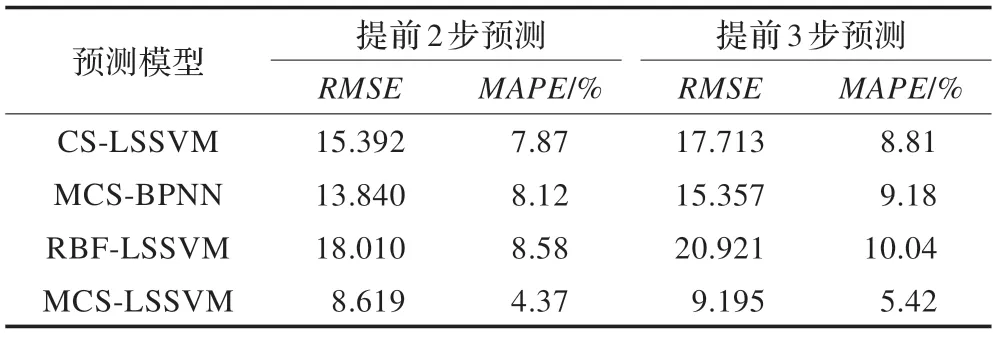
表2 MCS-LSSVM 与其他模型多步预测性能对比
4 结论
为了获得更优的卷烟销售量预测结果,提出一种MCS-LSSVM 的卷烟销售量预测模型,根据仿真实验可得如下结论:
(1)LSSVM 核函数及参数对卷烟销售量预测结果有较大影响,通过将二次多项式核函数和RBF 核函数进行组合,提高模型的通用性,并采用布谷鸟算法对参数进行自动寻优,克服了LSSVM 参数选择的盲目性。对比结果表明,改进布谷鸟算法比标准布谷鸟算法寻优能力更强,提高了卷烟销售量预测精度。
(2)相对于BP 神经网络,LSSVM 解决了神经网络在训练样本少的情况下过拟合的缺陷,具有训练时间短及预测速度快等优点,为小样本下的卷烟销售量预测提供了有效的解决方案,具有较高的实用价值。
[1] 程永照.回顾与展望:卷烟经济研究文集[M].北京:世纪图书出版社,2003.
[2] 谢星峰.基于神经网络的卷烟销售预测模型的研究及应用[D].昆明:昆明理工大学,2006.
[3] 刘红飞.基于灰色系统理论的广东卷烟消费需求预测研究[J].经济师,2007,12(l):273-274.
[4] 沈航,邹平.可拓聚类预测方法预测卷烟销售量[J].昆明理工大学学报,2006,12(3):95-98.
[5] 罗艳辉,吕永贵,李彬.基于ARMA 的混合卷烟销售预测模型[J].计算机应用研究,2009,27(7):2664-2668.
[6] 谢东风,邹平.基于CBP 的卷烟销售二重趋势时间序列预测模型研究与应用[J].控制理论与应用,2007,24(6):1015-1020.
[7] 罗艳辉,吕永贵,李彬.混合卷烟销售预测模型[J].计算机工程与设计,2009,30(20):4744-4747.
[8] 孙兰兰,宋雯斐.CPSO 和LSSVM 融合的网络入侵检测[J].计算机工程与应用,2013,49(9):90-93.
[9] 刘静.基于AFSA-LSSVM 的短时交通流量预测[J].计算机工程与应用,2013,49(17):226-229.
[10] 张大为,段哲民,李鹏,张晓辉.遗传优化的LSSVM 在故障诊断中的仿真研究[J].计算机仿真,2010,27(10):164-167.
[11] 熊南,刘百芬.基于自适应粒子群优化LSSVM 的网络流量在线预测[J].计算机应用与软件,2013,30(9):21-24.
[12] Sadollah A,Bahreininejad A,Eskandar H.Mine blast algorithm:A new population based algorithm for solving constrained engineering optimization problems[J].Applied Soft Computing,2013,13(5):2592-2612.
[13] 赵专政,李云翔.聚类加权和CS-LSSVM 的文本分类[J].计算机工程与应用,2013,49(16):124-128.
