一种基于双精度搜索算法的变论域模糊控制
2015-04-16刘培奇孙阳阳
刘培奇,田 洋,孙阳阳
LIU Peiqi,TIAN Yang,SUN Yangyang
西安建筑科技大学 信息与控制工程学院,西安710055
College of Information&Control Engineering,Xi’an University of Architecture&Technology,Xi’an 710055,China
1 引言
相对于传统控制方式,模糊控制(FC)凭借其不需对象模型、鲁棒性强、实时性好等优点广泛用于非线性、时变滞后系统中。然而模糊控制器实质上是插值器,插值精度与模糊规则数量紧密相关,提高精度必然以扩大规模为代价,导致其控制精度存在一定局限性[1]。变论域模糊控制器(VUFC)不仅可以综合专家知识,而且在不增加规则数量的情况下,论域随误差变小而收缩并随误差增大而扩展,从一定程度上解决了控制精度和控制复杂度的矛盾[2]。理论上分析,VUFC 的决策速度与精度应相对理想,可伸缩因子的定式结构使其自适应能力有限,控制无法达到预期效果[3]。同时模糊系统基本处于黑箱状态,被控对象多具有高度的非线性、强耦合等特性,因此定式伸缩因子很难有效避免控制函数畸变产生,尽管在控制精度上有较大提高,但却无法保证控制品质的最优性[4]。在模糊规则确定好的情况下,仅通过系统状态来调节VUFC 伸缩因子,必然使其因调节负担过重而不能得到理想输出。
近年来,VUFC 参数优化问题受到人们的关注,这也成为改善VUFC 精度和控制函数畸变的最有效方法,许多智能优化算法在这一研究中得到广泛应用。文献[5]利用遗传算法(GA)优化VUFC 的部分参数,但GA要进行复制、交叉和变异操作,不能及时利用网络的反馈信息,算法的搜索速度慢,且其性能对参数有较大依赖性。文献[6]提出一种基于粒子群算法(PSO)的变论域模糊控制策略,但PSO 种群在搜索空间中多样性的丢失使算法不够稳定,不是每次所得结果都能收敛到一个点。文献[7]通过引进具有在线学习和动态寻优能力的Q 学习算法(Q-learning)达到使控制器性能指标最小的目的,但Q-learning 学习时间较长,时间和空间复杂度相对较高。引力搜索算法(GSA)利用物体间的万有引力定理搜索最优解,是一种相对稳定的全局搜索算法,已成功实现参数辨识并应用于流程优化。本研究结合VUFC参数优化复杂度指标,在GSA 基础上结合序列二次规划搜索(SQP),提出一种双精度搜索算法。该算法在保留GSA 极强全局寻优能力基础上,进一步提高算法对最优解的局部搜索能力,并将改进算法用于等比因子智能寻优,构成一种基于双精度搜索算法的变论域模糊控制器。其目的是在减小伸缩因子调节负担的同时使控制函数畸变问题得到优化,进一步提高决策速度和控制效果。
2 控制算法基本原理
2.1 变论域模糊控制器
设双输入变量误差e和误差变化率ec的论域分别为X=[-E,E]、Y=[-EC,EC],控制输出变量u论域为Z=[-U,U],对应的语言变量为A、B、C且[8]:

式(1)是对论域X、Y、Z的模糊划分,xi、yj、zl分别是Ai、Bj、Cl的峰点,其中i=1,2,…,n,j=1,2,…,m,l=1,2,…,mn,并设定Ai、Bj、Cl均为可积函数。
由模糊推理规则可得到以下推理形式:
IfxisAi,andyisBj,thenuisCij.
其中i=1,2,…,n,j=1,2,…,m。
模糊控制系统可以表示成一个n元插值函数:

其中i=1,2,…,m,j=1,2,…,n。
变论域模糊控制实质是采用“粗略控制”到“精细控制”的策略,即当模糊控制器的输入(一般为误差E)较大时,采用“粗略控制”,论域随之膨胀;当模糊控制器输入较小时,采用“精细控制”,论域随之压缩。变化后的论域可以表示为:
X(e)=[-α1(e)E,α1(e)E]
Y(ec)=[-α2(ec)EC,α2(e)EC]
Z(e,ec)=[-β(e,ec)U,β(e,ec)U]
其中α1(e)、α2(ec)和β(e,ec)叫作论域的伸缩因子,e、ec都是时间函数,相对于变论域,原来的论域X、Y、Z叫作初始论域,基于式(2)的变论域模糊控制可以表示成如下n元动态插值函数:
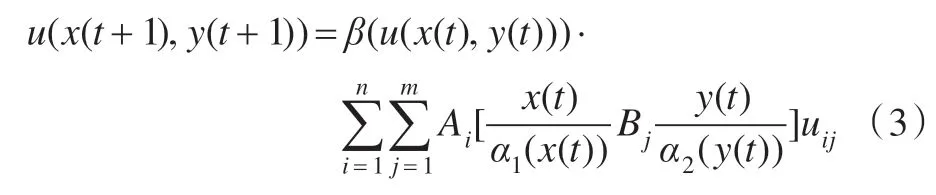
变论域模糊控制器较模糊控制器在自适应能力、控制精度等性能方面都得到了提升,并且变论域模糊控制器的控制规则的设计更为简单,它无需太多的专家知识和经验,只需要获取规则的大致趋势即可[9]。
在模糊规则设计好的情况下,对变论域模糊控制要求的关键部分在于输入、输出论域伸缩因子选择,输入、输出论域伸缩因子本文选择[10-11]:
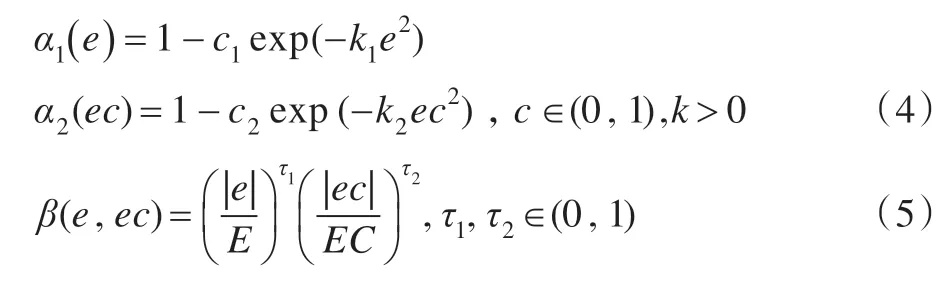
2.2 双精度搜索算法
GSA 是基于对群体的物理学万有引力进行模拟而提出的新的优化搜索技术,它通过群体中各粒子间的万有引力相互作用智能指导搜索结果[12]。研究发现,GSA具有较好的全局优化能力,但局部搜索能力较差,在迭代的早期,算法具有较好的寻优性能,但在后期会出现在局部最优解附近“振荡”的现象,趋同化严重,易早熟。SQP 是轨迹优化中应用较为广泛的一种约束非线性优化算法,其收敛速度快,可靠性高,国内外许多大型优化软件都是基于该算法编写的,但该算法需要一个较好的初始点[13]。本研究结合两者特点,首先利用GSA 的全局搜索能力进行初始优化,将优化结果提供给SQP 作为初始点,这种串行优化策略结合了GSA 和SQP 的优点,具有较强的全局和局部搜索能力,同时算法的计算速度和精度都有明显提高。在改进算法中,由于采用“全局-局部”双重精度的搜索机制,因此定义为双精度搜索算法(Double Precision Search Algorithm,DPSA)。算法流程如图1 所示。
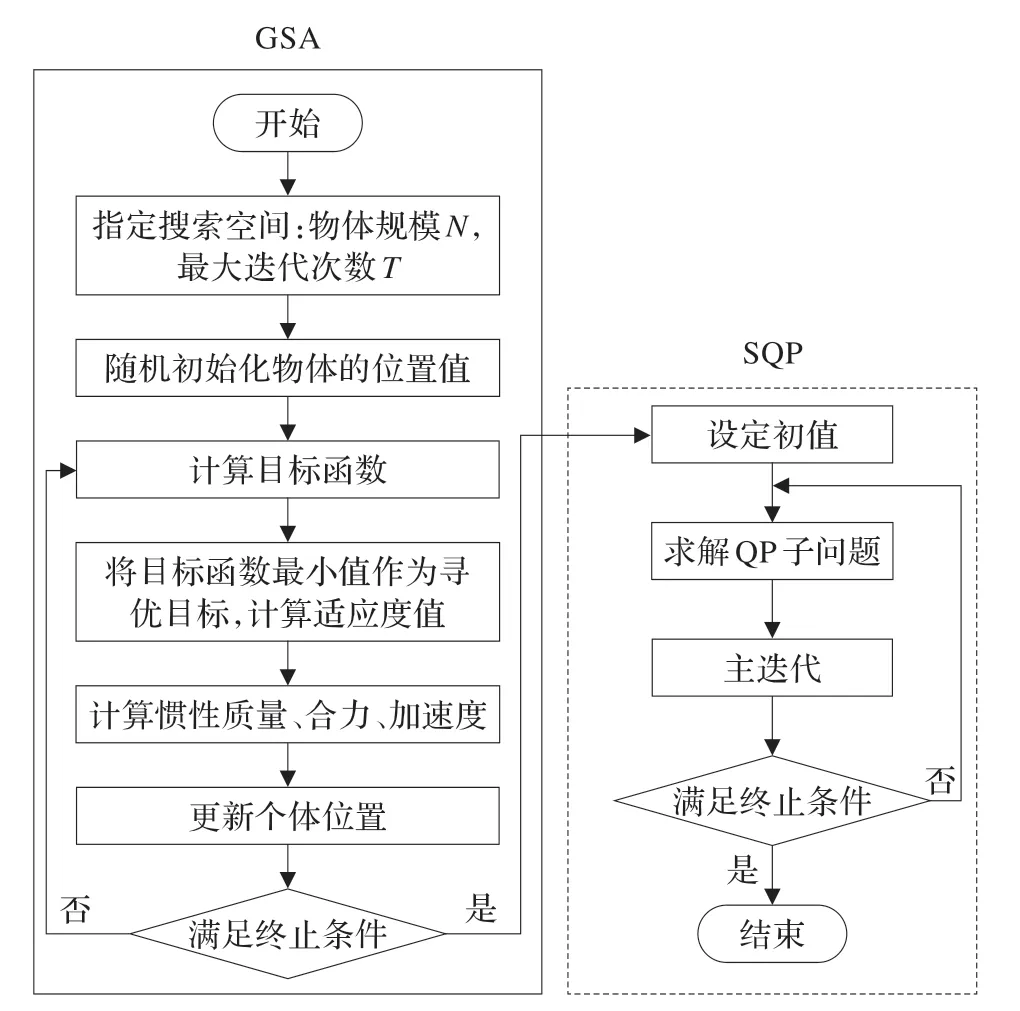
图1 算法流程图
3 基于双精度搜索算法的变论域模糊控制
3.1 等比因子
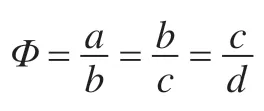

图2 不同Φ 值时不同形式的隶属度函数
3.2 性能指标
VUFC 参数优化是一类特殊的优化问题,需要采集系统输入输出数据构建目标函数。目标函数的选取对优化问题求解极为关键,必须准确反映优化目标。对于控制系统参数优化问题,目标函数的构建以获取最优控制性能指标为依据。控制理论中常见的指标有绝对误差积分指标IAE、平方误差积分指标ISE、时间平方误差乘积积分指标ITSE和时间绝对误差乘积指标ITAE。ITAE指标与其他几类指标相比能更好反映系统控制品质[15-16],ITAE指标目标函数离散形式定义为:

3.3 控制器设计与分析
利用DPSA 和VUFC 各自的优势,设计基于双精度搜索算法的变论域模糊控制器(DPSA-VUFC),系统结构如图3 所示。
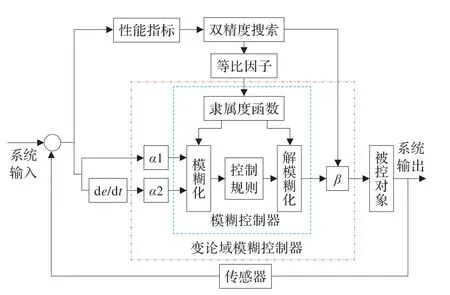
图3 基于双精度搜索算法的变论域模糊控制结构图
在本设计中,用变论域模糊控制器中的伸缩因子调节论域大小进行外调节,而等比因子无法改变论域大小进行内调节,内外结合。这样的设计后,等比因子调节不但减轻了伸缩因子的调节负担,而且当在变论域过程中由于隶属度函数发生改变,以致输出控制函数发生畸变时,表现为外部性能指标ITAE变大,等比因子就会配合调节,迫使指标变小。
目标函数变量及优化变量为VUFC 等比因子Φ,DPSA 通过在解空间中搜索调整Φ值来获得目标函数最小值,从而求取最优Φ值。当J(ITAE)值较大时,即误差e较大,为使误差e快速进入稳定区域,论域应进行一定的扩展,等比因子应该配合伸缩因子快速粗调,即Φ>1;当J(ITAE)值较小时,误差e接近稳定区域,为了提高控制精度,减少模糊集峰点之间的距离即论域收缩的同时,等比因子配合伸缩因子细调节,即Φ<1。
定式变论域模糊控制相当于保持等比因子不变,只调整论域的大小,而等比因子无法调整论域大小,却可以调节隶属度函数,两者结合使用起到互补的效果,可使模糊控制器的性能接近最优。
4 算法仿真
同步发电机励磁控制系统在稳态和暂态过程中都会直接影响发电机的性能,优良的励磁系统不仅可以保证高质量的电能、发电机运行可靠性和稳定性,而且可以有效地提高发电机及其相关电力系统的技术经济指标。励磁控制系统由放大单元、励磁机、同步发电机、测量传感器和变论域模糊控制单元组成,其模型可用图4传递函数框图表示[16-17]。其中K为各环节放大系数,V为环节输出,τ为时间常数,Vo为系统输出即为机端电压。
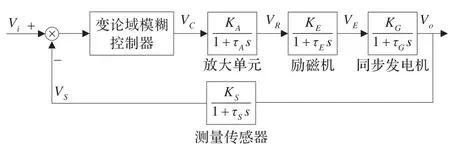
图4 励磁控制系统传递函数框图
4.1 系统参数设置
超调作为励磁系统动态控制过程中最重要的指标,能直接反应控制系统的稳定性。本实验采用综合考虑ITAE指标与超调量的目标函数来获得更优的控制品质:
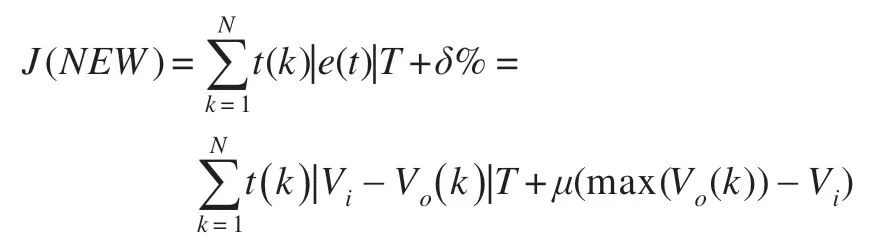
等式右边前一项为指标ITAE,后一项为超调量;μ为相对权重参数。
为了验证DPSA-VUFC 控制方法的有效性,进行同步发电机励磁控制系统的Matlab仿真实验,模型如图4所示,参数设置:KA=10,τA=0.1,KE=1,τE=0.5,KG=0.6,τG=1,KS=1,τS=0.01。
仿真系统实验按照本文设计优化策略和算法进行。分别采用GA、PSO 和DPSA 作为优化器,搜索目标函数。GA 参数:种群规模N=40,迭代次数n=500,交叉率Pc=0.7,变异率Pm=0.05;PSO 参数:种群规模N=40,迭代次数为n=500,c1=c2=2。DPSA 参数:种群规模N=30,G0=20,α=1,c1=c2=0.5。
VUFC对于输入量e和ec,基本论域为[-60,60]和[-10,10],对于所有输入输出变量的离散论域都为[-6,6]。变论域采用将量化因子Ke、Kec分别除以对应伸缩因子,比例因子Ku乘以对应的伸缩因子的等价处理办法:Ke=6/60=0.1,Kec=6/10=0.6,Ku=1。相应模糊集{NB,NM,NS,ZO,PS,PM,PB},控制决策表如表1 所示。伸缩因子依式(4)、(5),参数取为:c1=0.5,c2=0.8,k1=1.0,k2=1.5,τ1=0.3,τ2=0.9。控制器采用三角形隶属度函数,并采用加权平均法将模糊量精确化。

表1 模糊控制规则表
4.2 实验结果分析
考虑到算法的随机性,为了达到测试结果的稳定,对于给定模型,每个算法独立运行 20 次取其统计结果,包括最小值、最大值、平均值和标准差,每次的初始点均由计算机随机产生。统计数据表2 为20 次重复实验不同优化方法获得的最优目标函数值统计结果,表3为对应超调量统计结果。
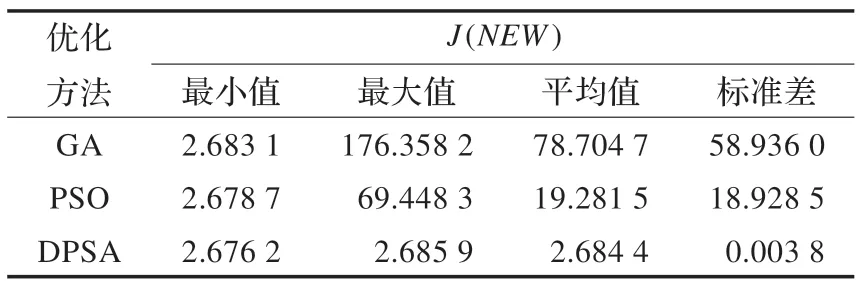
表2 不同优化方法所得最优目标函数值
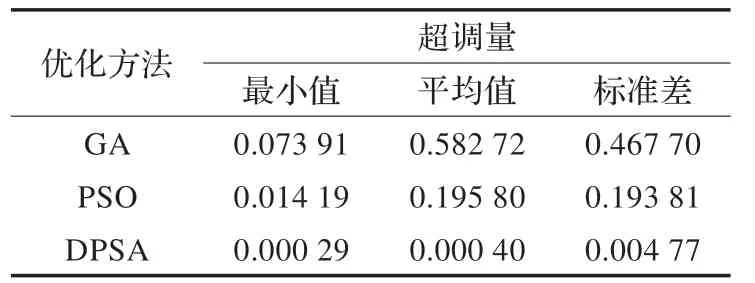
表3 不同优化方法所得超调量
分析表2 可知,DPSA 得到的最优目标函数最小值和最大值大小基本相等,而GA 和PSO 最优目标函数最小值和最大值大小相差大,较DPSA,GA 的差距甚至达到了102数量级,并且DPSA 最优目标函数平均值和方差两项指标明显小于其他两种方法。通过比较20 次计算的均值可以发现,DPSA 均值几乎与最优值相同,而GA 和PSO 均值与最优值有不小的差距。因此DPSA 得到的最优目标函数结果显现出明显的优势,表明其在方法的稳定性上表现突出。由表3 可知,DPSA 得到的超调量平均值和标准差明显小于GA 和PSO,进一步说明其在寻优过程中的稳定性更好。
图5 和图6 为3 种不同控制方式搜索20 次获得的等比因子Φ对应的调节过程仿真曲线。其中图5 为20 次结果中最优Φ值对应的调节过程,图6 为平均最优Φ值对应的调节过程。两组仿真曲线表明,采用DPSA-VUFC控制方式在快速性、准确性上都优于其他两种控制方式,超调量极低且稳定性最好。GA 和PSO 在两组实验中表现不够满意,是由于算法本身稳定性不够造成的。20 次重复实验中,部分优化结果效果良好,部分结果效果较差,从而影响了算法在参数寻优中的整体表现。而DPSA 稳定性高,优化效果平均,超调极小,几乎没有震荡,当收敛后即寻优结束后,能够快速进入稳定区。
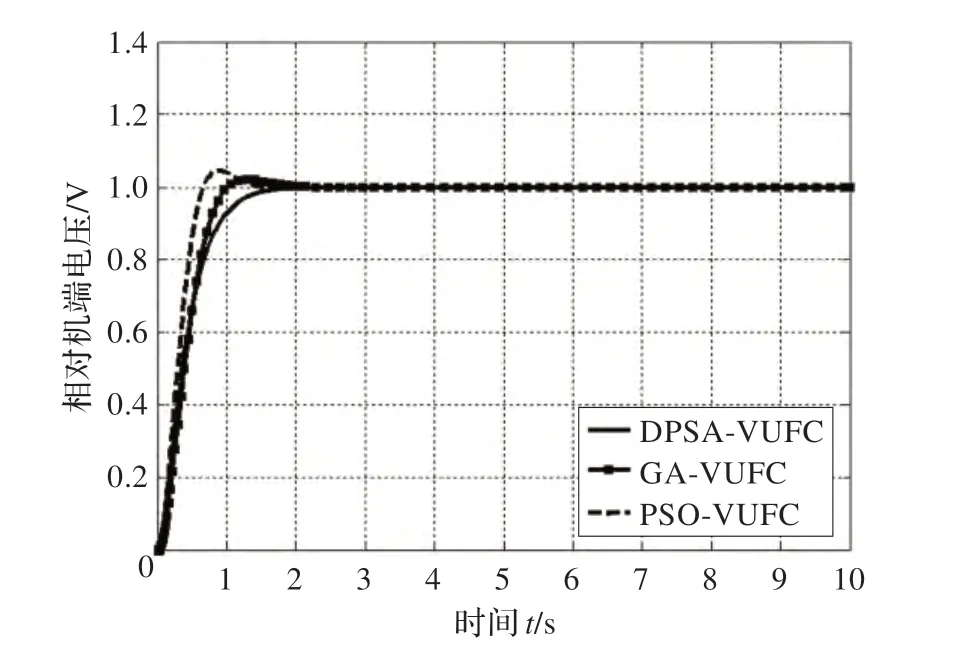
图5 最优Φ 值对应的调节过程
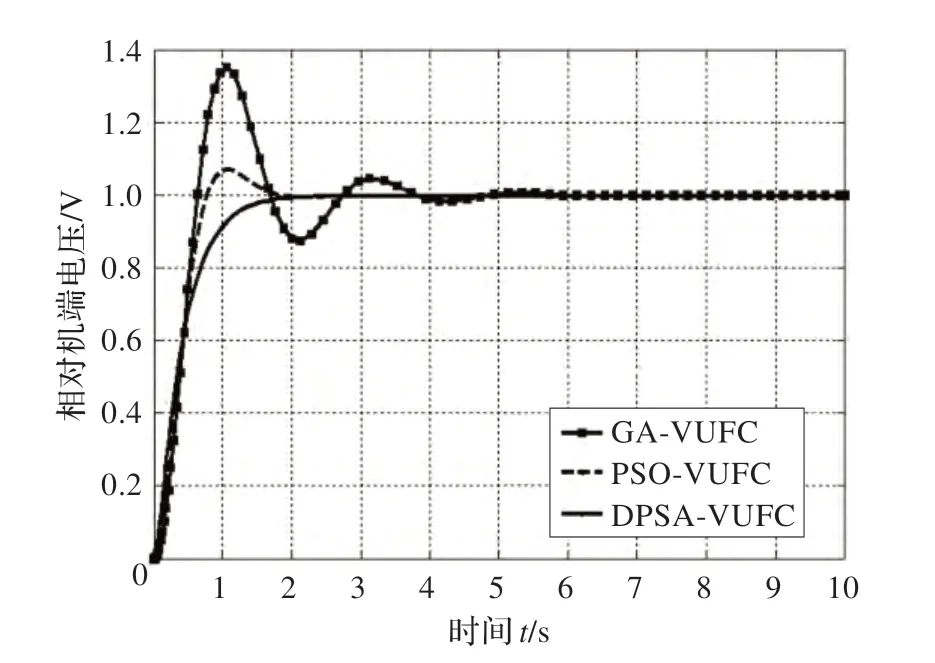
图6 平均最优Φ 值对应的调节过程
5 结束语
本文针对定式变论域模糊控制器伸缩因子控制压力大,控制函数在遗传复制中由于隶属度函数变化引起输入输出的变化等缺点,设计了基于双精度搜索算法的变论域模糊控制器。通过伸缩因子自适应调整模糊控制器论域,从而在不增加模糊控制规则的前提下使控制精度提高,而等比因子的调节分担了伸缩因子的调节负担,极大程度上克服了由于隶属度函数变化问题所带来的对控制器动态性能的影响。对比实验表明DPSA在参数寻优中的搜索能力明显优于其他两种算法且稳定性高,同时DPSA-VUFC 控制方式的收敛速度快,上升和调节时间短,其J(NEW)统计值也非常小,控制效果较其他两种控制方式都要理想。作为一种新型优化搜索算法,DPSA 具备在VUFC 参数优化中深入应用的潜力。
[1] Cheng Chibin.Fuzzy process control:construction of control charts with fuzzy numbers[J].Fuzzy Sets and Systems,2005,154(2):287-303.
[2] Mann G,Gosine R G.Three-dimensional min-max-gravity based fuzzy PID inference analysis and tuning[J].Fuzzy Sets and Systems,2005,156(2):300-323.
[3] 李洪兴.变论域自适应模糊控制器[J].中国科学:E 辑,1999,29(1):32-42.
[4] 李洪兴.非线性系统的变论域稳定自适应模糊控制[J].中国科学:E 辑,2002,32(2):211-223.
[5] 肖磊,张阿卜.一种基于遗传算法的新的模糊控制器优化方法[J].控制理论与应用,2005,24(10):1-3.
[6] 彭灵志.基于粒子群算法变论域的模糊控制策略研究及其应用[D].长沙:中南大学,2005:1-60.
[7] 余涛,于文俊,李章文.基于Q 学习算法的变论域模糊控制新算法[J].控制理论与应用,2011,28(11):1645-1650.
[8] 诸静.模糊控制理论与系统原理[M].北京:机械工业出版社,2005:212-214.
[9] Chen P C,Hsu C F,Lee T T.Fuzzy-identification-based adaptive back stepping control using a self-organizing fuzzy system[J].Soft Comput,2008,13(22):635-647.
[10] 邵诚,董希文,王晓芳.变论域模糊控制器伸缩因子的选择方法[J].信息与控制,2010,39(5):536-541.
[11] 赵云涛,王京,谢新亮,等.基于多层蚁群算法的变论域模糊控制[J].模式识别与人工智能,2009,22(5).
[12] Rashedi E,Nezamabadi-Pour H,Saryazdi S.GSA:a gravitational search algorithm[J].Information Sciences,2009,179(13):2232-2248.
[13] 付磊,安效民,覃曌华,等.基于混合遗传算法的多冲量最优变轨[J].航天控制,2013,31(3):15-19.
[14] 李家炜.一种新的优化模糊控制器算法[J].控制理论与应用,2002,19(2):279-281.
[15] Ogatt K.Modern control engineering[M].Upper Saddle River,NJ:Prentice Hall,1990.
[16] 李超顺,周建中,肖剑.基于改进引力搜索算法的励磁控制PID 参数优化[J].华中科技大学学报:自然科学版,2012,40(10):119-122.
[17] IEEE Power Energy & Society.IEEE Std421.1-86 IEEE standard definition for excitation systems for synchronous machines[S].Piscataway:IEEE Press,1986.
