基于CFD的液压锥阀开启过程流固耦合分析

， 　， 　(解放军理工大学 野战工程学院， 江苏 南京　210007)

引言

液压锥阀结构简单，较液压滑阀和球阀具有更好的密封性能，因此应用非常广泛。液压锥阀在开启过程流场不稳定，并且其性能对于液压系统有着较大的影响。流固耦合的研究可以追溯到19世纪初的机翼气动弹性问题[1]。当前，流固耦合的研究主要集中于水轮机、轴流泵[2-4]等，针对液压阀的研究并不多。文献[5]对液压阀进行了稳态的单向流固耦合计算，流固耦合分析结果表明阀芯受力较大，约为阀体的3倍，但其没有考虑阀芯开启过程的瞬态受力情况。因此，有必要对液压锥阀的阀芯进行重点研究，并分析其瞬态受力情况。针对上述问题，借助动网格技术和流固耦合理论，以流体力学软件CFD-ACE+为平台，对液压锥阀开启过程进行液阀的流固耦合分析，为改善液压锥阀内部流体流动状态和阀芯受力状况提供依据。

1　几何模型和网格划分

1.1　几何模型

借鉴文献[6]归纳出的具有共性的液压锥阀作为研究对象，其结构及尺寸见图1。

该锥阀的阀芯在开启过程中液压油的流动具有对称性，为提高计算效率，取流动区域和阀芯的一半作为研究对象，建立的用于流固耦合分析的几何模型如图2所示。

图1　液压阀结构

图2　锥阀流固耦合分析模型锥阀几何模型

1.2　网格划分

网格划分直接影响到计算精度和效率，网格过于稀疏会使精度降低，过于密集会使效率降低。根据研究对象的特点，本研究采用结构网格。网格划分采用处理软件GEOM实现，为更好地捕捉阀口处的流场变化，对阀口区域网格进行细化。在大量试算的基础上，最终确定网格总数为64087个。其中，流域网格47222个，阀芯网格16865个。网格划分情况如图3所示。

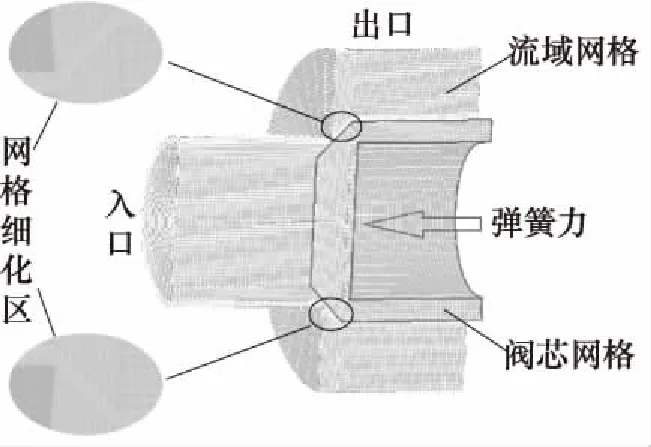
图3　网格划分

2　控制方程

2.1　动网格条件下的流场控制方程

在网格运动过程中，流场内控制体将发生改变，一般采用积分形式来表示诸守恒方程[7]：

(1)

2.2　流固耦合控制方程

在流固耦合交界面处应力：

(2)

式中， ΔFi为在i方向上的力，N；ΔAi为在i方向的受力面积，m2。

力平衡方程：

(3)

式中，σxx、σyy、σzz为应力分量；τxy、τxz、τyx、τyz、τzx、τzy为应变分量。

几何方程：

(4)

式中，ξxx、ξyy、ξzz为应变分量；u、v、w为速度分量；γxy、γyx、γzy、γyz、γxz、γzx为切应变分量。

本构方程：

式中，μ为泊松比；E为杨氏模量，GPa；G为切变模量，GPa。

3　边界条件与参数选取

3.1　流域参数

入口条件：压力入口，选取6.3 MPa；

出口条件：压力出口，设为大气压；

液压油：型号VG46，其密度ρ=885 kg/m3；运动黏度μ=46 mm2/s；由于液压油压缩性很小[8]，设为不可压缩流体；

弹簧刚度：125 N/mm；

湍流模型：采用k-ε湍流模型。

3.2　阀芯参数

阀芯材料为45号钢。密度ρ=7850 kg/m2；杨氏模量E=210 GPa；泊松比ν=0.3。

4　仿真结果分析

4.1　阀芯运动情况分析

阀芯的运动情况由阀口静压、液动力以及弹簧力共同决定，仿真得到的运动情况如图4所示。图中点1为阀芯开启初期(t=0.2 ms)，点3为阀芯位移最大时(t=0.55 ms)，点5为阀芯稳态位移时(t=5 ms)，点2、点4分别为波动幅度最大过程中位移相同速度相反的两点(t=0.4 ms、t=0.7 ms)。

从图4中可以看出在液压锥阀开启过程，阀芯位移存在一定的波动，最大位移达到0.00175 m，稳态位移为0.0011 m，位移的波动引起流量的波动，从而影响执行装置的运动情况；阀芯位移的波动会产生噪声和振动，也会影响流场及阀芯瞬态受力情况。

液压锥阀阀芯稳态位移的理论计算公式为：

(6)

式中，p为阀口静压，6.3 MPa；d为流道直径，12 mm；k为弹簧刚度，125 N/mm；Fl为阀芯所受的稳态液动力；ρ为液压油密度，885 kg/m3；Q为稳态流量；Cd为流量系数，锥阀为0.77～0.8，选取0.8；α为液压锥阀的半锥角，45°；A为过流面积；Δp为压差，6.3 MPa。

联立上式，可以解得阀芯稳态位移x0=0.001 m。

仿真得到的阀芯稳态位移xf=0.0011 m。理论计算与仿真计算结果的误差为9.1%，可以认为仿真计算结果与理论计算结果基本吻合，证明了仿真的可靠性。误差的产生是因为在理论计算中使用半锥角代替节流口处的液流角，且没有考虑液压锥阀内部结构不同及流场微观流动带来的影响。

4.2　流固耦合分析

阀芯开启初期(t=0.2 ms，图4中点1)、最大位移(t=0.55 ms，图4中点3)、稳态位移(t=5 ms，图4中点5)的仿真结果如图5所示。图中给出了液压锥阀流域的压力场、压力等值线分布以及液压锥阀阀芯所受的冯米斯应力。冯米斯应力是根据第四强度理论得到的一种当量应力，可以用来对疲劳、破坏等进行评价。

从图5可以看出：

(1) 在流场的H区域会产生负压，负压区域面积随着阀芯的运动而变大。流场负压区是引起气蚀的主要原因，气蚀会导致阀芯产生气蚀破坏；

(2) 在液压锥阀开启初期，阀芯应力集中于阀芯的A区域和B区域且四周对称分布，当阀口开度较大后，应力集中于B区域；

(3) 在阀芯开启过程中，液压锥阀阀芯同一位置所受应力是变化的。

阀芯运动过程中位移相同、速度相反的两点，即t=0.4 ms(图4中点2)和t=0.7 ms(图4中点4)的仿真结果如图6所示。

从图6可看出：虽然阀芯位移相同，但流域的压力场、阀芯的应力场均存在较大差异，这是由于阀芯运动的速度不同引起的；从图6b中可以看出，当阀芯运动的速度方向与流体流动方向相反时，流域压力较大，阀芯所受的应力也较大并且集中于阀芯的A区域。

综合图5、图6分析结果可知，液压锥阀阀芯所受应力主要集中于A区域和B区域，两点应力随时间的变化情况如图7所示。

从图7中可以看出：在液压锥阀开启过程中，最大瞬时应力和稳态应力均在A处，分别为15.3 MPa和12.3 MPa，均满足45号钢材料许用强度； A、B两处的应力会出现波动，B处的波动幅度更大，易产生疲劳破坏；阀芯开启初期，B处所受瞬时应力较大，随后A处应力较大。

5　结论

(1) 液压锥阀开启过程中流域会产生负压区，负压是产生气蚀的主要原因，可以对流域结构进行改进来减小或避免负压区域的产生；

图7　A和B两点应力变化情况

(2) 液压锥阀开启过程中不同位置阀芯所受应力是不断变化的，流场和应力场的分布不仅仅与阀芯位移有关，还与阀芯速度有关；

(3)液压锥阀开启过程中阀芯应力主要集中于两个区域，对该区域应力变化情况进行研究可以为改进阀芯结构、提高阀芯寿命提供依据。

参考文献：

[1]邢景棠,周盛,崔尔杰.流固耦合力学概述[J].力学进展,1997,27(1):19-37.

[2]Xiao R F, Wang Z W, Luo Y Y. Dynamic Stresses in a Francis Turbine Runner Based on Fluid-structure Interaction Analysis [J]. Tsinghua Science and Technology,2008,13(5):587-592.

[3]Saeed R A, Galybin A N, Popov V. 3D Fluid-structure Modelling and Vibration Analysis for Fault Diagnosis of Francis Turbine Using Multiple ANN and Multiple ANFIS [J]. Mechanical Systems and Signal Processing,2013,34(1-2):259-276.

[4]施卫东,王国涛,蒋小平,等.流固耦合作用对轴流泵内部流场影响的数值计算[J]. 流体机械,2012,(1):31-34.

[5]王慧,李济洋.液压支架用大流量液控单向阀流固耦合[J]. 辽宁工程技术大学学报,2014,(5):622-626.

[6]郑宁舟.锥阀流动仿真分析及其结构改进[D].西安：长安大学,2011.

[7]何晓晖,孙宏才,程健生,等. 基于动网格的液压阀阀芯启闭中的液动力分析[J]. 解放军理工大学学报,2011,(5):491-495.

[8]Zhi-fei Peng, Chun-geng Sun, Rui-Bo Yuan, Peng Zhang. The CFD Analysis of Main Valve Flow Field and Structural Optimization for Double-nozzle Apper Servo Valve[J]. Procedia Engineering,2012,(31):115-121.