高速内啮合齿轮轴减速器扭转振动传递矩阵法分析

　，

(北京航空航天大学 自动化科学与电气工程学院， 北京　100191)

引言

减速器是传动系统的重要组成部分。齿轮啮合过程的激励特性，系统所传递的动力特性以及输出端负载特性，必然会激起传动系统的振动以及传动系统和机匣(箱体)结构间的相互耦合振动[1]。减速器传动系统的动力学特性会对其工作性能的实现和工作可靠性产生重要的影响，国内外均对各类减速器传动系统动力学特性的研究高度重视。扭转振动会给传动系统带来重大问题，甚至导致灾难性后果[2]。高速齿轮减速器的扭转振动分析，给系统的可靠性和优化设计等研究提供有力支撑。

从已有的研究看，目前对于齿轮传动系统的扭转振动分析通常有两种方法：有限元方法(FEM, Finite Element Method)和传递矩阵方法(TMM， Transfer Matrix Method)[3]。有限元法通过二阶微分方程建立转子轴承系统，具有计算精度高，更能贴近曲轴实际工作情况等特点，但因其计算规模巨大，通常被用于系统的控制设计和估计[4]。而传递矩阵法通过将链状传动结构离散化成为一系列集中惯量、集中刚度的集总参数模型，因其分析计算链式结构振动快捷有效等特点，被广泛用来解决动力学问题[5,6]。

文献[7]利用传递矩阵法分析直升机旋翼试验台传动系统的振动特性，找到了系统自激振动产生的原因，发现振动发散与试验台主轴支撑刚度有关。文献[8]研究表明，增加轴段数量或增大轴承刚度可以降低直升机机尾传动系统的固有频率。文献[9]用传递矩阵方法分析了直升机动力传动系统扭转振动以及系统的振动特性，推导了直升机动力传动系统特有并车级和行星级齿轮传递矩阵模型。文献[10]利用传递矩阵法分析计算了复杂分支结构的车辆动力传递系统扭振的固有频率及振型。文献[11]采用传递矩阵法对多轴转子系统和齿轮啮合的多轴传动系统线性和非线性振动问题进行了深入研究。文献[12]通过重新定义复值状态向量，引入外部支撑刚度、阻尼和旋转参考系等，改进传统传递矩阵法，得到复合传递矩阵法(Complex Transfer Matrix)，克服了传统方法的两大不足。

本研究针对某型小尺寸高速内啮合齿轮轴减速器结构及动力学特点，采用传递矩阵法将其结构离散化，建立了系统的集总参数模型(轴盘模型)，分析计算了系统固有频率和各阶主振型，讨论了其振动特性。

1　高速内啮合齿轮轴减速器

某燃气涡轮-泵动力装置地面试验系统主要由中频电机、超越离合器、涡轮、减速器、液压油泵等组成，其内部结构如图1所示。高速内啮合齿轮轴减速器是该燃气涡轮-泵动力系统的核心部分。

1.中频电机　2、7.轴承　3.壳体　4.燃气涡轮　5.外齿轮轴　6.内齿轮轴　8.液压缸图1　涡轮动力装置的内部结构示意图

该动力装置地面试验时，中频电机驱动外齿轮轴提供动力，中频电机的稳定输出转速为15000 r/min。动力装置经由齿轮传动减速后，驱动柱塞轴向柱塞液压泵旋转，输出增压油液，为电液伺服机构提供工作介质。

如图1，该结构齿轮传动采用内啮合方案，动力装置外轮廓尺寸为202 mm×150 mm×150 mm，体积小，结构紧凑。齿轮轴减速器是该型电液伺服系统的重要组成部分，结构为一级齿轮传动，啮合形式为内啮合，齿轮形式为普通圆柱齿轮。

2　扭转振动传递矩阵模型

先做如下假设：将内、外齿轮等效为均质圆盘； 不计入齿轮啮合变形；假设基座对壳体的支承刚度足够大，轴承对齿轮轴的支承刚度足够大，内外齿轮轴的质心无横向位移，无弯曲变形。则两个齿轮轴只有绕中心轴线旋转的自由度。

在假设条件下对系统做离散化：

将内啮合齿轮传动结构简化为无质量的梁上带有若干集中质量的扭转振动系统——轴盘系统。把减速器结构中的涡轮、外齿轮和内齿轮处理为集中质量的刚体圆盘，各集中质量间的轴段简化为无质量扭转弹簧[13]。把传动系统按链状结构，划分为一系列单元(一个典型单元包括一个无质量的轴段和一个作为刚体考虑的圆盘)。

在不影响计算的情况下，约定各截面上的转角θ和扭矩M都为正值。

图2所示为内啮合齿轮轴传动系统的轴盘扭振模型。

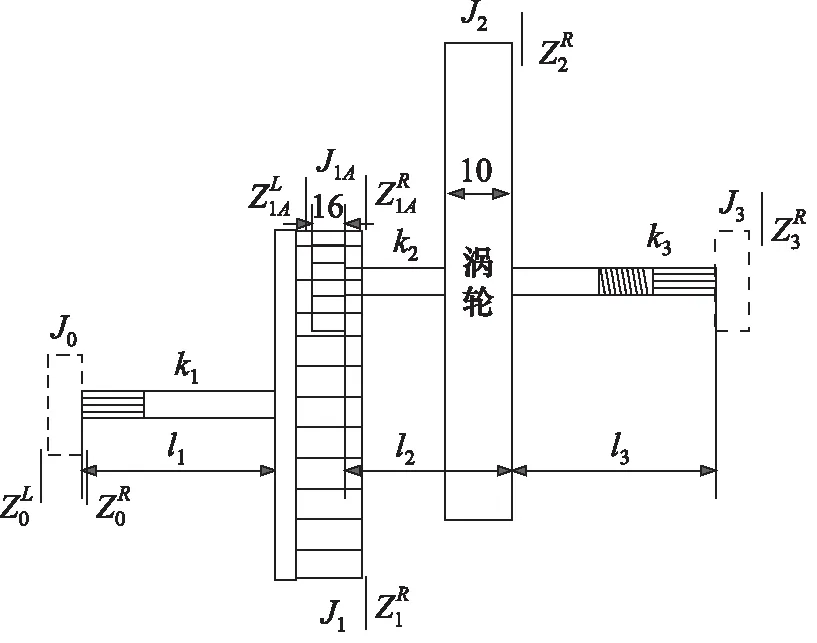
图2　内啮合减速器的轴盘扭振模型

图3所示为轴、盘两端的受力情况。

图3　等效轴段和圆盘的受力情况示意

将任一截面上的转角及扭矩排成列向量Z，则：

(1)

(2)

其中场传递矩阵:

(3)

同理，由圆盘的运动微分方程，写出传递关系:

(4)

其中点传递矩阵:

(5)

有式(2)、式(4)得到第i单元的传递矩阵Hi：

(6)

依据上述定义列出相邻状态向量间的传递关系：

(7)

(8)

(9)

(10)

(11)

(12)

得出系统最左端与最右端的状态向量之间的传递关系为：

(13)

记总传递矩阵为H，则：

(14)

3　轴盘模型解算分析

3.1　模型解算

作为ω函数的传递矩阵已经满足了各个单元的运动微分方程，若试算出同时还能满足边界条件的ω值，则该值即为系统的某一阶固有频率。

表1　扭转振动参数表

ω4J0J1-k1ω2(J1+J0)]/4k1k2+(k3-ω2J3)·

(4ω4J0J2-4k1ω2J2)/k1k3+(k3-ω2J3)·

(k2-ω2J2)[16ω4J0J1A-16ω2k1J1A+

ω4J0J1-k1ω2(J1+J0)]/4k1k2k3

(16)

图4　余扭矩变化曲线

表2　扭转振动固有频率

表3　各主振型计算值

系统各阶主振型如图5所示。

3.2　结果分析

动力装置的两种驱动方式，其激励源特性如表4所示。可以看到，当动力装置由中频电机驱动时，减速器啮合频率稍大于系统扭转振动的2阶固有频率。燃气涡轮驱动时，啮合频率稍大于系统3阶、4阶固有频率。

图5　扭转振动各阶主振型

转速r·min-1转频Hz啮合频率/Hz对比固有频率/Hz中频电机驱动1500025040003674.57燃气涡轮驱动40000667106728054.99/8253.61

模型的解析结果与地面实验时的情形吻合，如图6所示，当中频电机转速接近13800 r/min时(啮合频率3680 Hz)，系统振动加剧，转速继续提高，达到15000 r/min时(啮合频率4000 Hz)，稍趋平稳。

图6　地面试验振动频域图

4　结论

燃气涡轮-泵动力装置地面试验系统在高速驱动时发生剧烈谐振，为找到谐振原因，本研究应用传递矩阵法对该系统进行了扭转振动的动力学分析，建立了内啮合传动系统的轴盘模型，并进行了模型解析，得到结论如下：

(1) 分析了内啮合齿轮轴的振动力学特性，计算了系统的各阶固有频率和主振型，为以振动信号分析为基础的故障诊断提供了支撑；

(2) 轴盘模型解析结果得到了系统扭振固有频率和主振型，解释了地面试验时，电机高速旋转接近最高转速过程中， 系统剧烈谐振的原因。当燃气涡轮驱动

减速装置动力输出时，也应使燃气涡轮转速尽量迅速远离共振区域(系统3阶、4阶固有频率范围，即8054.99～8253.61 Hz)；

(4) 不计入系统中阻尼影响时，传递矩阵法只需要对一些阶次较低的联系矩阵阶乘运算，数值求解较为简单，计算工作量不大。

参考文献：

[1]毛振中. 某型直升机主减系统振动特性与控制稳定性[D].北京：北京航空航天大学, 2008.

[2]Sankar S. On the Torsional Vibration of Branched Systems Using Extended Transfer Matrix Method[J]. Journal of Mechanical Design, 1979, 101(4): 546-553.

[3]Wu J S, Chen C G. Torsional Vibration Analysis of Gear Branched Systems by Finite Element Method [J]. Journal of Sound and Vibration, 2001, 1(240):159-182.

[4]Thomson W T. Theory of Vibration with Applications[M]. Prentice-Hall, Englewood Cliffs, New Jersey,1981.

[5]Hsieh S, Chen J, Lee A. A Modified Transfer Matrix Method for the Coupling Lateral and Torsional Vibrations of Symmetric Rotor-bearing Systems[J]. Journal of Sound and Vibration,2006,289(1-2):294-333.

[6]邓晓晓,张保成. 内燃机轴系扭转振动综述[J]. 研究与开发, 2012,(1):76-82.

[7]Xunwen S,Shaoping W,Dongmei Z.Vibration Analysis and Experiment of the Helicopter Rotor Test Stand Transmission[C]// Fluid Power and Mechatronics (FPM), 2011 International Conference on Fluid Power and Mechatronics.Beijing： IEEE ,2011: 202-206.

[8]朱自冰，朱如鹏，鲍和云，等.刚度对直升机尾传动系统弯曲振动固有频率影响的分析[J].航空动力学报，2009,24(1)：176-180.

[9]王建军，毛振中，卿立伟，等.直升机动力传动系统扭转振动整体传递矩阵分析[J].航空动力学报，2008,23(10)：1805-1812.

[10]冯栋梁,魏来生.传递矩阵法在动力传动系统扭振分析中的应用[J].车辆与动力技术, 2010(1):41-45.

[11]Choi S T, Mau S Y. Dynamic Analysis of Geared Rotor-bearing Systems by the Transfer Matrix Method [J]. Journal of Mechanical Design, 2001, 123(4):563-568.

[12]Varney P, Green I. Rotor Dynamic Analysis Using the Complex Transfer Matrix[C]//ASME 2012 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Chicago, IL, USA, 2012: 237-246.

[13]倪振华.振动力学[M].西安：西安交通大学出版社,1989.