PAM仿生肘关节运动学逆解建模及验证

　， ， ， 　， (东北大学 机械工程与自动化学院， 辽宁 沈阳　110819)

引言

气动人工肌肉(Pneumatic Artificial Muscle，简称PAM)，由于其柔性特性，故其较传统的气动执行机构具有结构简单、输出力重量比大、能量转换效率高、仿生性能好等优点[1]。用其作为仿人机械手臂的驱动器，能够降低成本，提高机构的柔顺性能。目前国内外不断对气动肌肉仿生机械臂的结构进行研究与开发，并取得了许多瞩目的成果[2-4]。

然而，在对仿生机械臂结构的研究过程中，建立机构精确的运动学模型是首要问题，它是对机构力学、误差及控制等问题进行研究分析的基础和保障。气动肌肉仿生机械臂作为一种柔性机构，目前对其运动学的建模方法包括有限元法、几何分析法、伪刚体模型法等。其中有限元法由于对初始条件要求苛刻，很难作为柔性机构运动学分析的有效方法[5-7]；几何分析方法主要针对具有分布柔度的全柔性机构，但目前该方法并没有统一的步骤，只能根据具体结构确定适宜的算法，不具备通用性[8]；伪刚体模型法，于1986年由I.Her首次提出[9]，其适用于部分柔性机构以及集中式全柔性机构，对于具有分布柔度的全柔性机构则存在很大缺陷[10-12]。

本研究针对一种三自由度气动肌肉仿生肘关节，首先根据机构特点，建立其伪刚体模型，并以此求得仿生肘关节的运动学逆解方程；其次，根据所建方程，在不同运动轨迹条件下，对气动肌肉长度变化进行仿真分析；最后，根据伪刚体模型，构建机构的虚拟样机，搭建气动肌肉仿生肘关节的仿真系统模型，从而对所建运动学逆解模型的准确性进行验证。

1　机构描述

3-DOF 气动肌肉仿生肘关节模型如图1所示，该仿生肘关节由前臂圆盘1、上臂圆盘2、虎克铰3、气动肌肉4及支撑杆5等组成。7个虎克铰分别安装在前臂圆盘及上臂圆盘上，其中1个虎克铰安放在前臂圆盘的中心点处，其余按圆盘内接正三角形分别安放在前臂圆盘及上臂圆盘上；3根气动肌肉分别通过虎克铰与前臂圆盘及上臂圆盘相连，且与虎克铰之间存在轴向转动；支撑杆上端通过虎克铰与前臂圆盘中心点相连，并与虎克铰之间存在轴向转动，下端通过螺纹与上臂圆盘中心点固连。通过驱动3根气动肌肉，控制其内部压力及流量，从而实现前臂圆盘的旋转。

图1　气动肌肉仿生肘关节模型

2　机构逆运动学方程的建立

由于气动肌肉为柔性件，则气动肌肉仿生肘关节为刚-柔混合机构，故可利用“伪刚体模型法”建立气动肌肉仿生肘关节的运动学方程，将气动肌肉视为圆柱副，由2个构件组成，其伪刚体模型如图1所示。由于支撑杆与上臂圆盘固连在一起，故视为一个构件，则，该仿生肘关节拥有8个构件，10个运动副，其中7个万向副，3个圆柱副，1个转动副，根据Kutzbach Grubler公式可求得机构的自由度为：

=6(8-10-1)+2×7+2×3+1

=3

(1)

建立如图1所示的空间坐标系。首先，在上臂圆盘中心点处建立固定坐标系OB-XB、YB、ZB，其中XB轴过上臂圆盘铰链点B3，YB轴与边B1B3相交且与边B1B2平行，ZB轴垂直于上臂圆盘向上；然后，在前臂圆盘中心点处建立运动坐标系Op-Xp、Yp、Zp，同固定坐标系，其XP轴过前臂平台铰链点b3，YP轴与边b1b3相交且与边b1b2平行，ZP轴垂直于前臂圆盘向上。l1、l2、l3分别为三根气动肌肉B3b3、B2b2、B1b1的长度。将固定坐标系OB-XB、YB、ZB作为参考坐标系，设机构转动顺序为Zp-Yp-Xp，则运动坐标系Op-Xp、Yp、Zp相对其的旋转矩阵R为：

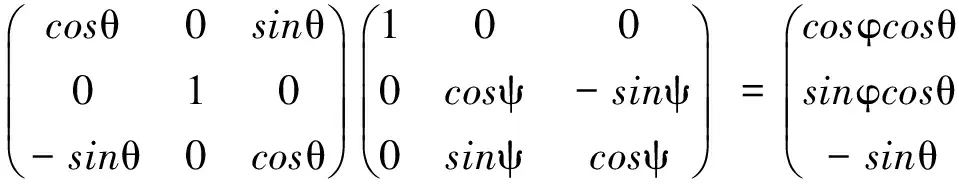
(2)

式中，(ψ、θ、φ)分别为前臂圆盘相对固定坐标系XB、YB、ZB轴的转角。为方便计算，将式(2)的旋转矩阵描述为：

(3)

由于前臂圆盘与上臂圆盘半径相等，即rP=rB=r，则虎克铰bi、Bi(i=1,2,3)在其各自坐标系中的位置坐标为 ：

(4)

(5)

运动坐标系Op-Xp、Yp、Zp原点相对于固定坐标系OB-XB、YB、ZB的位置坐标可表示为P=(0，0，z)T，则两圆盘相应铰链点之间的连杆矢量为：

liei=P+Rbi-Bi(i=1,2,3)

(6)

将虎克铰bi、Bi的坐标代入式(6)，并取矢量模，则有杆长的标量方程式。将式(5)平方展开后，消去ei，则可得到各根气动肌肉的长度为：

2Bix(bixxl+biyxm)-2Biy(bixyl+biyym)+

2bixzzl+2biyzzm+z2(i=1,2,3)

(7)

根据旋转矩阵正交性，即RRT=E，则式(7)可化为：

2Biy(bixyl+biyym)+2bixzzl+

2biyzzm+z2(i=1,2,3)

(8)

将式(4)及式(5)代入式(8)中，并对其开平方，则可得到3根气动肌肉长度变化方程为:

(9)

方程组(9)即为该气动肌肉仿生肘关节的逆运动学方程。

对方程组(9)两端求导即可得到机构速度逆解方程，即：

vl=J-1vp

(10)

式中,vl=(vl1,vl2,vl3)T，vP=(ωψr,ωθr,ωφr)T，J-1为vp的系数矩阵，即该机构的Jacobian矩阵逆矩阵。

对式(10)两端再次进行求导，则可得到机构的加速度方程，即：

(11)

3　运动学逆解数值算例

设机构上臂圆盘及前臂圆盘的半径均为38.5 mm，运动坐标系Op-Xp、Yp、Zp原点相对于固定坐标系OB-XB、YB、ZB的位置坐标为P=(0，0，250)T，根据式(9)，对气动肌肉仿生肘关节在不同运动轨迹下的逆运动学问题进行仿真，其结果如图2所示。

当前臂圆盘相对XB轴旋转时，与XB轴对称的两根气动肌肉，在长度变化上亦呈现出对称性，而另外一根垂直相交于XB轴的气动肌肉长度则没有发生改变(如图2a所示)； 当前臂圆盘相对YB轴旋转时，与XB轴对称的两根气动肌肉，其长度变化曲线相同，而另外一根气动肌肉长度变化曲线的幅值大于其他两根，且相位与其相差180°(如图2b所示)；当前臂圆盘相对ZB轴旋转时， 三根气动肌肉的长度变化曲线相同(如图2c所示)； 当前臂圆盘相做圆周运动时， 三根气动肌肉长度变化曲线的相位彼此之间相差120°(如图2d所示)；由图3可以看出，尽管参考点的运动轨迹不同，但三根气动肌肉长度的变化均是连续的，平稳的，且没有突变，说明机构在运动过程中，具有良好的平滑性。

图2　气动肌肉长度变化曲线

4　逆运动学方程的验证

为了进一步验证所求气动肌肉仿生肘关节逆运动学方程的准确性，根据机构伪刚体模型，在MATLAB/Simulink 中建立关节机构虚拟样机及其仿真系统模型，如图3所示。

根据式(9)，计算得到气动肌肉理论长度，并将其与实际长度的差值作为PID控制器的输入，通过调节PID参数，得到机构前臂圆盘转角轨迹曲线，并与期望轨迹进行对比，其结果如图4所示。

由图4可以看出，通过调节PID模块，前臂圆盘转角轨迹曲线与期望轨迹曲线基本吻合，其误差变化如图4b、图4d所示，从而验证了所建机构运动学逆解数学模型的准确性。

5　结论

本研究针对三自由度PAM仿生肘关节，首先建立机构的伪刚体模型，并根据模型求得机构运动学逆解方程；其次，根据所的方程完成对机构运动学逆解数值仿真分析；最后，根据伪刚体模型构建气动肌肉仿生肘关节的虚拟样机，搭建仿真系统模型，根据运动学逆解方程，从而实现对虚拟样机的PID控制，进而验证逆解方程的准确性。

仿真结果表明，在设计工作空间内，三根气动肌肉的长度变化连续、平稳且没有突变，说明机构在运动过程中，具有良好的平滑性。此外，通过调节PID控制器参数， 气动肌肉仿生肘关节前臂圆盘转角轨迹曲线与期望轨迹曲线重合度较高，从而实现了对逆解方程准确性的验证，增强了仿真结果的可靠性，为机构运动性能、力学性能等方面的分析奠定了基础。

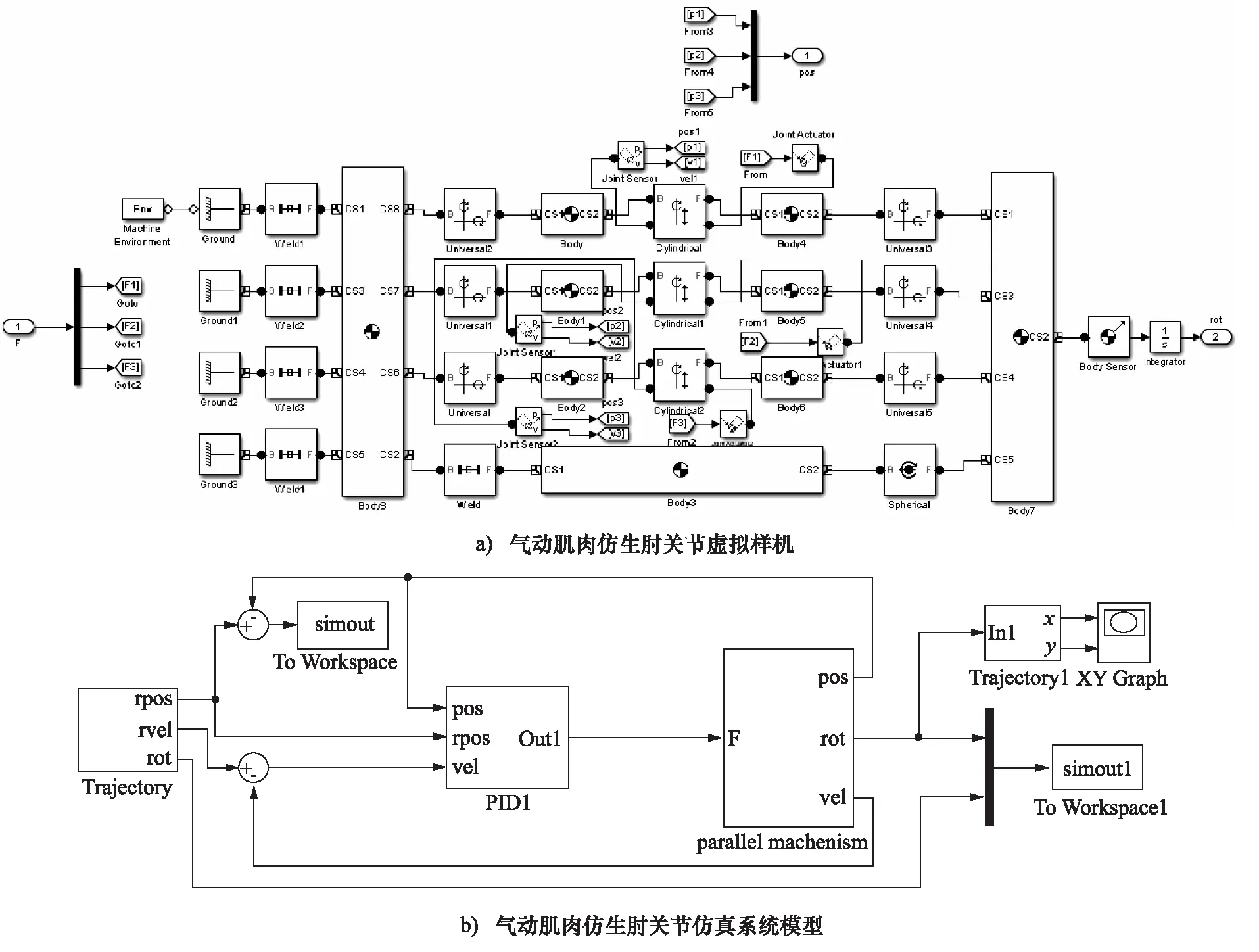
图3　气动肌肉仿生肘关节虚拟样机及仿真系统模型

图4　控制仿真结果

参考文献：

[1]Kawamura K,Peters II R A,Beget S,et al.Intelligent Robotic Systems in Service of the Disabled[J].IEEE Transactions on Rehabilitation Engineering,1995,3(1):14-21.

[2]C Tommasino P,Caligiore D,Sperati V,et al.A McKibben Muscle Arm Learning Equilibrium Postures[C].4th IEEE RAS & EMBS International Conference on Biomedical Robotics and Biomechatronics (BioRob), IEEE,2012:1229-1234.

[3]Tanaka D,Kamo D,Watanabe T,et al. Development of a 7-DOF Manipulator Actuated by Straight-fiber-type Pneumatic Artificial Muscle[C].2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM),IEEE,2013: 300-306.

[4]应申舜,秦现生,任振国,等. 基于人工肌肉的机器人驱动关节设计与研究[J]. 机器人,2008,30(2):142-146.

[5]杨毅,丁希仑,吕胜男,等. 基于有限元的平面变胞机构运动学研究[J]. 航空学报,2010,1(12): 2425- 2434.

[6]R Avile′s,A Herna′ndez,E Amezua,et al. Kinematic Analysis of Linkages Based in Finite Elements and the Geometric Stiness Matrix[J]. Mechanism and Machine Theory,2008,43(8): 964-983.

[7]Satoko HIRABAYASHI,Tomonari TSUCHIDA,Eiichi TANAKA,et al. Simulation Study on Mechanisms of Hip Fractures in Backward Falls[J]. Journal of Biomechanical Science and Engineering,2013,8(4): 328-243.

[8]胡海燕,王鹏飞,孙立宇,等. 线驱动连续型机器人的运动学分析与仿真[J]. 机械工程学报,2010,46(19): 1-8.

[9]I Her,A Midha. A Compliance Number Concept for Compliant Mechanisms,and Type Synthesis[J]. Journal of Mechanical Design,1987,109(3): 348-355.

[10]邱丽芳,翁海珊,柳林,等. 全柔性四杆机构伪刚体模型分析计算方法的改进[J]. 农业机械学报,2008,39(5): 142-145.

[11]Dana Vogtmann,Satyandra K Gupta,Sarah Bergbreiter. Modeling and Optimazation of a Miniature Elastomeric Compliant Mechanism Using a 3-Spring Pseudo Rigid Body Model[C]. ASME 2013 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Portland,2013.

[12]Kuber. Development of a Methodology for Pseudo-rigid-body Models of Compliant Segments with Inserts,and Experimental Validation[D]. Missouri: Missouri University of Science and Technology,2013.