液压驱动单元力控系统建模及其性能影响因素研究

　， ， 　， ,3

(1. 燕山大学 河北省重型机械流体动力传输与控制实验室， 河北 秦皇岛　066004； 2. 燕山大学 机械工程学院， 河北 秦皇岛　066004； 3. 燕山大学 先进锻压成形技术与科学教育部重点实验室， 河北 秦皇岛　066004)

引言

液压驱动相比电机和气压驱动，具有功重比大、承载能力高、响应快等优点，液压驱动型足式机器人现已成为国内外高性能仿生机器人领域的研究热点，这类机器人在战场运输、险境搜救和外星探测等领域具有广阔的应用前景。近年来，美国波士顿公司成功研制出高性能四足仿生机器人Big-Dog，该机器人可以在冰面、沙石地面、森林以及草地中平稳行走。我国也高度重视该类液压驱动型四足机器人的研究，并于2010年将“高性能四足仿生机器人”列入“863”计划，支持多家高校相继开展样机的研发工作[1-4]。

液压驱动单元作为液压驱动型四足机器人的关节驱动器，其工作性能的好坏直接影响机器人的整体运动控制效果。一般而言，各关节的液压驱动单元多采用高精度位置伺服控制，以保证机器人足端的位置精度，但当机器人足端触地或接触障碍物时，如果继续采用位置控制会产生较大冲击，易引起四足机器人的不稳定，甚至造成机身及其附带的电子设备的损坏。此时需将四足机器人某些关节的液压驱动单元(诸如髋关节横摆液压驱动单元)切换为高精度力伺服控制或者主动柔性控制，以有效地减缓系统冲击，提高机器人的整体稳定性。可见，液压驱动单元的力伺服控制相比于位置伺服控制，也具有同等重要的作用，国内外学者在机器人关节力伺服系统的控制方法方面，也开展了大量的研究工作[5-9]。而力控方法的研究需基于较准确的力控系统数学模型，并掌握主要工作参数及给定信号对力控性能的影响，以便设计力控方法时可以依据力控系统的实际工况进行有针对性的动态补偿。

本研究介绍液压驱动单元结构组成原理，采用机理建模的方法，建立其力控系统数学模型，利用MATLAB/Simulink仿真平台建立力控系统仿真模型，在液压驱动单元性能测试实验台上测试液压驱动单元的力控性能，并与仿真曲线进行对比，以研究不同工作参数和给定信号对液压驱动单元力控性能的影响，为其力控方法的研究提供参考。

1　液压驱动单元力控系统数学建模

1.1　液压驱动单元结构原理

液压驱动单元作为高性能四足仿生机器人的核心部件之一，是由流量伺服阀、伺服缸、力传感器和位移传感器组成，其三维装配图如图1所示。

图1　液压驱动单元三维装配图

该液压驱动单元为四通滑阀控对称伺服缸结构，其结构原理图如图2所示。

图2　液压驱动单元结构原理图

该液压驱动单元作为液压驱动型四足机器人的关节驱动器，其设计参数如表1所示。

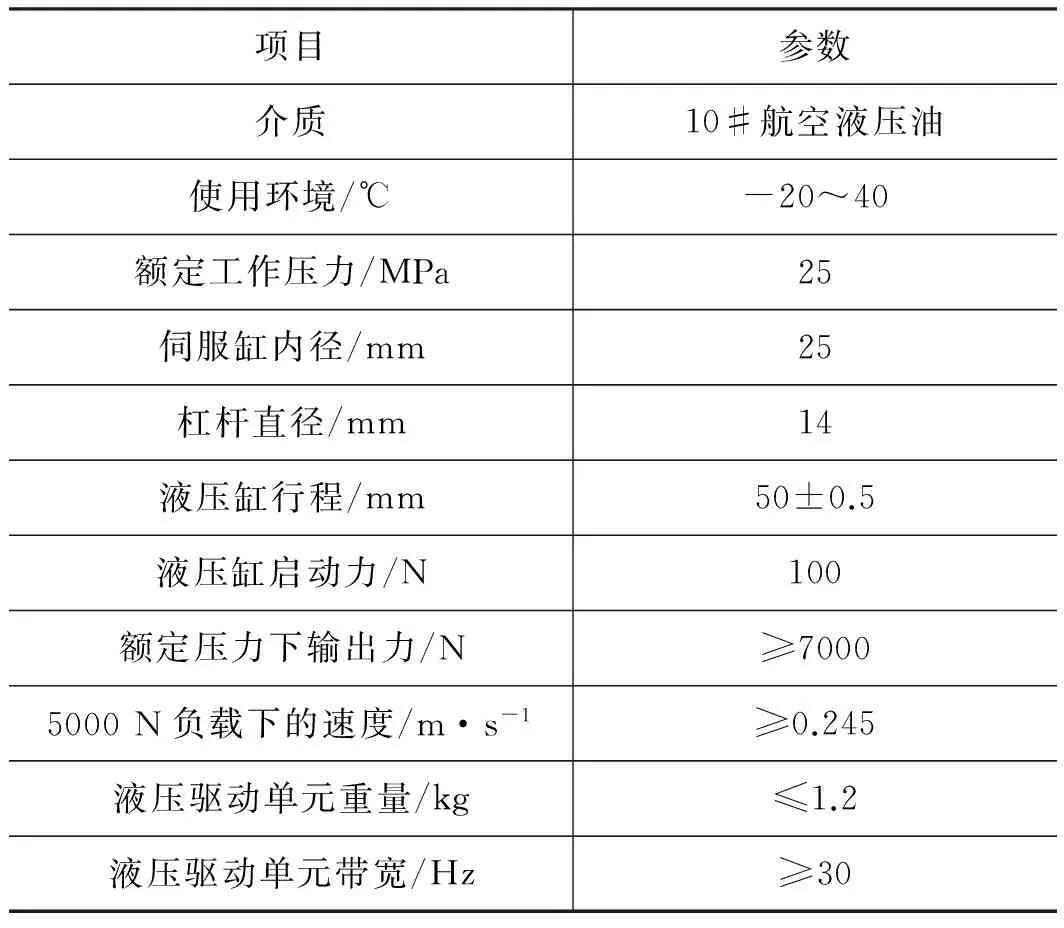
表1　液压驱动单元主要设计参数

为提高液压驱动单元的响应能力，该流量伺服阀选用小型力反馈两级喷嘴档板伺服阀；为减小液压驱动单元的重量以使机器人具有更大的负重能力，伺服缸本体采用高强度的铝合金加工而成；其双出杆对称缸结构，消除了非对称缸存在的往返速度非线性问题；伺服阀与伺服缸之间采用集成化安装，省去了阀与缸之间的连接管道，有利于缩小安装空间并减小长管路容积效应对液压驱动单元性能的影响，以提高液压固有频率；高精度力传感器和位移传感器分别安装在活塞杆端和伺服缸缸体外侧，实时检测液压驱动单元的输出力和活塞杆位移，进而实现液压驱动单元的高精度力闭环和位置闭环控制。

为建立液压驱动单元较完整的力控系统数学模型，后续将分别推导液压驱动单元各环节的传递函数。

1.2　流量伺服阀的数学模型及参数辨识

1) 滑阀级流量方程

由于液压驱动单元的伺服缸实际有效工作面积远小于普通液压缸，伺服阀输出流量微小的变化都将直接影响活塞杆的输出位移和速度，若采用线性化方法对伺服阀滑阀特定工作点进行局部线性化处理，将不能真实反映伺服阀整个动态过程的流量输出特性，因此考虑压力-流量非线性因素，得到伺服阀进油流量为:

(1)

伺服阀回油流量为:

(2)

式中,xv—— 液压驱动单元伺服阀阀芯位移

ps—— 系统供油压力

p1—— 液压驱动单元伺服缸左腔压力

p2—— 液压驱动单元伺服缸右腔压力

p0—— 系统回油压力

Kd—— 等效流量系数

等效流量系数Kd的表达式为:

(3)

式中,Cd—— 滑阀节流口流量系数

W—— 滑阀的面积梯度

ρ—— 航空液压油密度

2) 滑阀位移与电压的传递函数

理论上通过伺服阀力矩马达运动方程、衔铁挡板组件的运动方程、挡板位移与衔铁转角的关系和喷嘴挡板至滑阀的传递函数，可推导出力反馈电液伺服阀的传递函数，但伺服阀传递函数所涉及的诸多内部参数很难获得，因此本节通过辨识的方法确定伺服阀传递函数涉及的参数值。

对力反馈两级喷嘴挡板伺服阀而言，一般情况下力矩马达控制线圈和滑阀的固有频率均远大于衔铁挡板组件的固有频率，可将力矩马达控制线圈的动态和滑阀的动态忽略；作用于挡板上的压力反馈要远小于力反馈的影响，可将压力反馈回路忽略。此时，伺服阀的传递函数可近似等效为惯性环节与二阶振荡环节的乘积，因此伺服阀阀芯位移与输入功率放大器的电压信号之间的传递函数可简化为:

(4)

式中,Ka—— 伺服阀功率放大器增益

Kxv—— 伺服阀增益

Kvf—— 力反馈回路开环放大系数

ωmf—— 伺服阀固有频率

ζmf—— 伺服阀阻尼比

将式(4)的分母进行因式展开，可得到分母3阶传递函数的各系数项表达式:

(5)

其中，

本研究选用的伺服阀产品样本中给出了在开口度为25%和100%时伺服阀的频域特性曲线，考虑到伺服阀在进行力控过程中，一般工作在阀芯小开口范围内，因此依照25%开口度时的频域特性曲线进行参数辨识。基于MATLAB仿真平台，采用最小二乘法可辨识得到伺服阀三阶传递函数的各未知系数项数值为：

a=1.346×10-9，b=2.954×10-6，

c=3.347×10-3

(6)

联立式(6)和式(7)，可求得式(4)分母各参数的数值，并进行圆整，如表2所示。

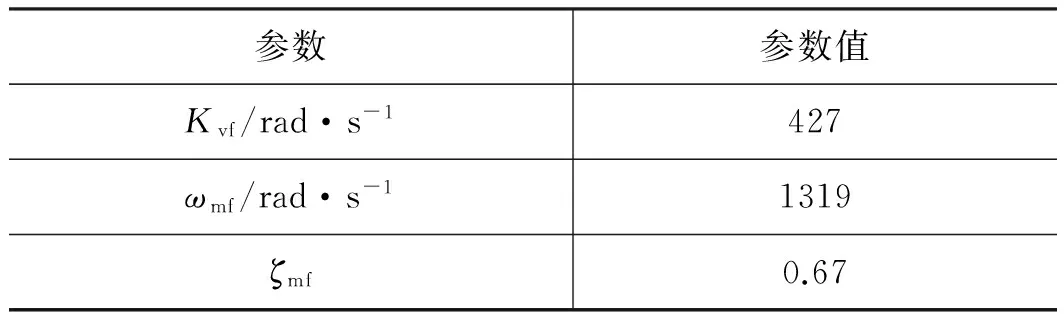
表2　伺服阀传递函数中的参数表

1.3　阀控缸系统基本方程

1) 流量连续性方程

依据流量连续性方程，可得伺服缸进油流量和进油腔容积为：

(7)

伺服缸回油流量和回油腔容积为:

(8)

式中,Ap—— 伺服缸活塞有效面积

xp—— 液压驱动单元伺服缸活塞位移

Cip—— 伺服缸内泄漏系数

Cep—— 伺服缸外泄漏系数

βe—— 有效体积弹性模量

V01—— 液压驱动单元进油腔初始容积

V02—— 液压驱动单元回油腔初始容积

由于液压驱动单元进/回油流道均开设于伺服缸缸体内部，其容积甚至小于伺服缸运动过程中产生的容积变化，因此考虑伺服缸活塞初始位置的不同，可得到以下表达式:

(9)

式中,Vg1—— 伺服阀与伺服缸进油连接流道容积

Vg2—— 伺服阀与伺服缸回油连接流道容积

L—— 伺服缸活塞总行程

L0—— 液压驱动单元伺服缸活塞初始位置

2) 力平衡方程

伺服缸输出力和负载力平衡方程为:

Kxp+FL+Ff

(10)

式中,mt—— 折算到伺服缸活塞上总质量，包括负载、活塞、位移传感器、力传感器、连接管道和伺服缸内油液以及其他动件的折算质量和

K—— 液压驱动单元负载刚度

Bp—— 负载及液压驱动单元的阻尼系数

Ff—— 负载及液压驱动单元的库仑摩擦力

FL—— 作用在液压驱动单元活塞上的任意外负载力

3) 传感器数学模型

所选用的力传感器的固有频率为控制系统采样频率的5倍以上，因此将传感器传递函数等效为比例环节，其反馈电压与伺服缸活塞杆受力的传递函数为:

(11)

式中,KF—— 力传感器增益

F—— 力传感器检测的力信号

2　液压驱动单元力控系统仿真建模

2.1　液压驱动单元力控系统框图

联立式(1)～式(4)和式(7)～式(11)，可建立液压驱动单元力控系统框图如图3所示。

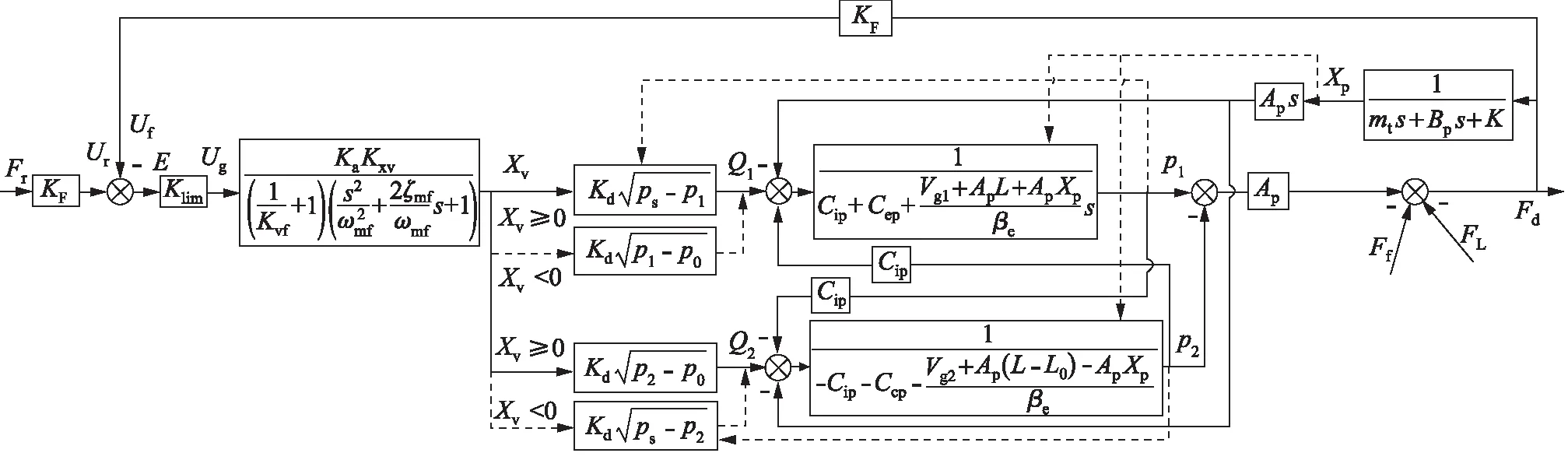
图3　液压驱动单元力控系统框图

2.2　力控系统各环节仿真模型

依据图2液压驱动单元力控系统框图，在MATLAB/Simulink仿真平台上分别建立力控系统各主要环节的仿真模型，其中，伺服阀流量-伺服缸两腔压力、电压偏差-伺服阀阀芯位移、伺服阀阀芯位移-伺服阀流量的仿真模型分别如图4至图6所示。

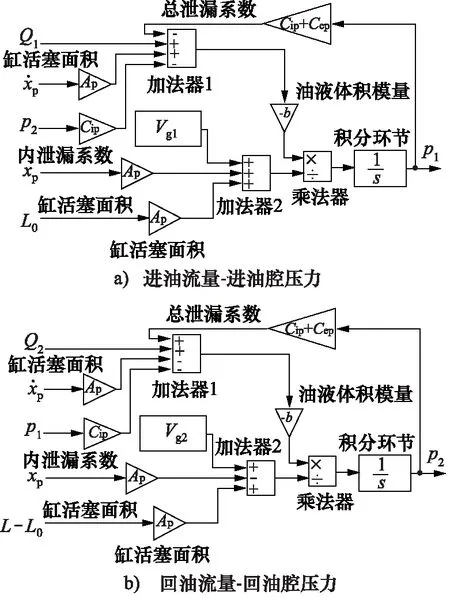
图4　伺服阀流量-伺服缸两腔压力仿真模型

图5　电压偏差-伺服阀阀芯位移仿真模型

图6　伺服阀阀芯位移-伺服阀流量仿真模型

2.3　力控系统整体仿真模型及参数

连接图4至图6，采用MATLAB/Simulink中子模型功能进行封装，建立的液压驱动单元力控系统仿真模型如图7所示。

忽略液压驱动单元的外泄漏，系统仿真模型中的参数及初值如表3所示。

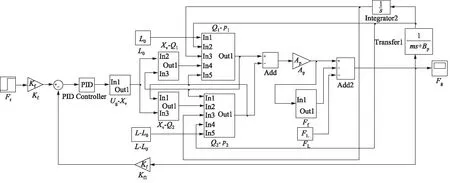
图7　液压驱动单元力控系统整体仿真模型

参数初始值伺服阀增益Kxv/m·A-10.05伺服阀功率放大器增益Ka/A·V-10.009伺服缸活塞有效面积Ap/m23.368×10-4进油腔管道容积Vg1/m36.2×10-7回油腔管道容积Vg2/m38.6×10-7伺服缸活塞总行程L/m0.05伺服缸活塞初始位置L0/m0.03系统供油压力ps/MPa7系统回油压力p0/MPa0.510#航空液压油密度ρ/kg·m30.867×103伺服缸外泄漏系数Cep/m3(s·Pa)-10伺服缸内泄漏系数Cip/m3(s·Pa)-12.38×10-13折算到伺服缸活塞总质量mt/kg1.1315有效体积模量βe/Pa8×108负载刚度K/N·m-15×105阻尼系数Bp/N(m·s-1)-12000折算流量系数Kd/m2·s-11.248×10-4力传感器增益KF/V·N-17.7×10-4

3　液压驱动单元力控性能测试实验台

3.1　力控性能测试实验原理

为更好地研究液压驱动单元力控模型的准确性并分析力控系统的性能，搭建专用于液压驱动单元的力控性能测试实验台，其原理示意图如图8所示。

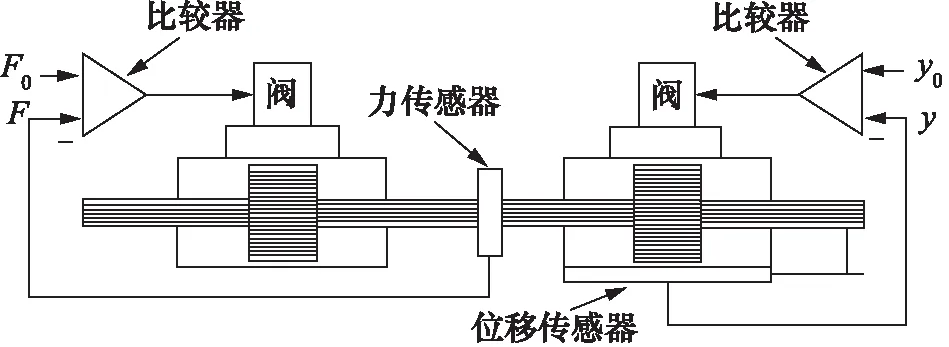
图8　液压驱动单元力控性能测试实验台组成示意图

实验台由两套相同的液压驱动单元组成。在进行液压驱动单元力控性能实验时，左侧液压驱动单元采用力闭环控制，称为被测试液压驱动单元；右侧液压驱动单元采用位置闭环控制，称为负载特性模拟液压驱动单元；被测试液压驱动单元和负载特性模拟液压驱动单元之间通过力传感器刚性连接。其液压原理图如图9所示。

3.2　力控性能测试实验台软硬件组成

液压驱动单元力控性能测试实验台实物照片如图10所示。

控制器采用由德国某公司开发的半实物仿真平台dSPACE，其实物图、控制界面及控制模型如图11所示。

1.截止阀　2.定量泵　3.电机　4.溢流阀　5.高压高精过滤器　6.单向阀　7.蓄能器　8.dSPACE控制器　9.伺服阀功率放大器 10.电液伺服阀　11.伺服缸　12.力传感器　13.位移传感器　14.电磁换向阀　15.风冷却器图9　液压驱动单元力控性能测试实验台液压原理图

图10　液压驱动单元力控性能测试实验台

液压驱动单元中主要元件的型号及性能指标参数如表4所示。

4　液压驱动单元力控性能影响因素研究

4.1　工作参数对力控性能的影响

1) 不同比例增益下的阶跃响应特性

设定伺服缸活塞杆初始位置L0=30 mm，系统供油压力ps=7 MPa，给定F=1000 N的阶跃力输入，分别调定控制器比例增益Kp=1、3和5时，测试液压驱动单元力阶跃响应曲线，并与仿真曲线对比，如图12所示。

由图12可以看出，3种比例增益下液压驱动单元力控系统的实验上升时间分别为53 ms、16 ms、10.6 ms， 最大超调量分别为0、0、5.8%，稳态误差分别为171.1 N、63.2 N、37.4 N，即随着控制器比例增益Kp的增加，力控制系统的响应速度提高，超调量增大，稳态误差减小，其原因为比例增益直接影响系统前向通道增益，从而影响系统稳、快、准三方面性能。

图11　控制器及其相关程序和界面

元件名称元件型号性能参数及说明生产销售厂家电液流量伺服阀200-0029额定流量:7L/min,额定电流:10mA,25%输入信号时的带宽:120Hz,阶跃响应时间:4ms,最大工作压力:31.5MPa,滞环≤3%(不加颤振),分辨≤1%(不加颤振),14MPa压力下的内泄漏≤0.7L/min,另外,该伺服阀外形尺寸小,长宽高尺寸为42mm×34mm×41.2mm,重量:230g,结构紧凑,便于集成安装英国star有限公司伺服阀功率放大器STE0005输入信号:±10V,输出信号:0～150mA,提供振颤信号、零点调整、主控输入环节、反馈输入环节、电源电压指示,可以完成功率放大器上的PID参数手动调节,用于驱动伺服阀实现电液位置、速度和力闭环控制英国star有限公司位移传感器GA09-25量程:±25mm,精度:0.5%,供电电压:15V,输出信号:0～10V上海极典电子有限公司力传感器WMC-13kN量程:0～13kN,精度:0.2%,供电电源:15V,输出信号:-10～10V上海宝宜威机电公司液压泵25PCY14-1B排量:25mL/r,额定转速:1500r/min,公称压力:31.5MPa启东恒宇液压设备公司

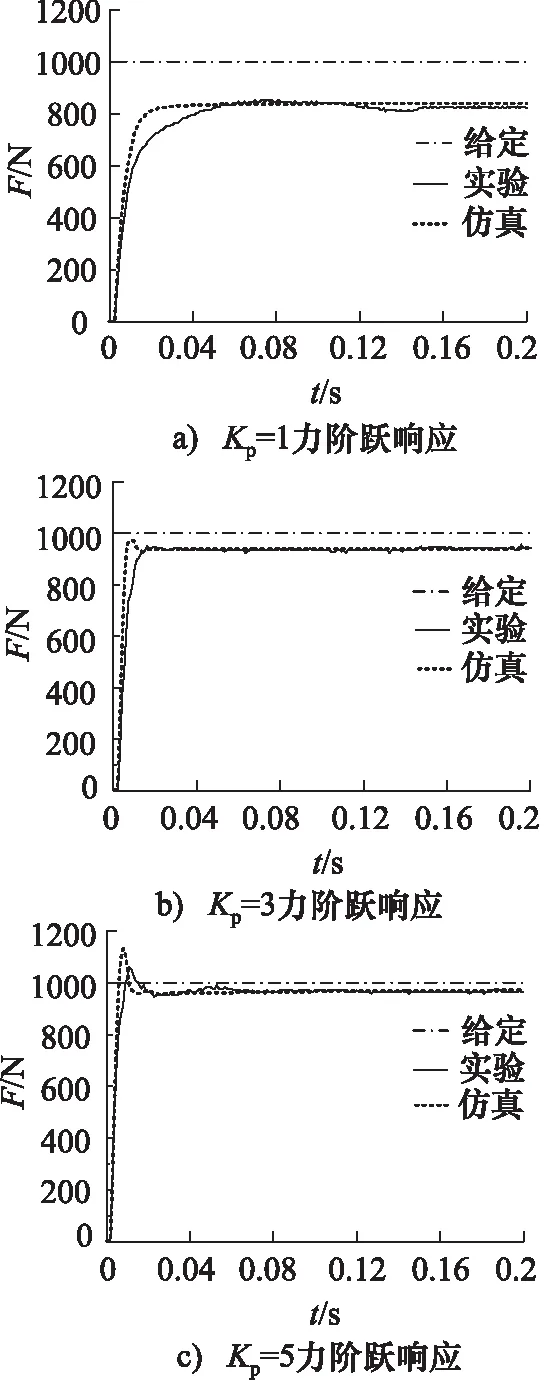
图12　不同比例增益下力阶跃响应仿真与实验曲线

相比于实验曲线，仿真曲线的响应时间较快，超调量较大，这是由于仿真模型不可能完全描述实际力控系统的全部特性，会存在一定的偏差，但仿真得出的总体趋势与实验分析结果是一致的，由此可知采用本研究建立的仿真模型进行定性分析，其结果是较为准确的。在本研究后续的力控系统分析时，为保证分析结果的准确性，实验数据将作为定量的分析结果，仿真数据仅作为参考。

2) 不同供油压力下的阶跃响应特性

设定伺服缸活塞杆初始位置L0=30 mm，控制器比例增益Kp=3，给定F=1000 N阶跃力输入，通过溢流阀分别调定系统供油压力ps=3 MPa、5 MPa和8 MPa，测试液压驱动单元力阶跃响应曲线，并与仿真曲线对比，如图13所示。

4.2　给定信号对力控性能的影响

1) 不同力阶跃量下的力控特性

设定伺服缸活塞杆初始位置L0=30 mm，系统供油压力ps=7 MPa，控制器比例增益Kp=3，分别给定F=500 N 、1000 N、1500 N和2000 N力阶跃输入时，测试液压驱动单元力阶跃响应曲线，并与仿真曲线对比，如图14所示。

图13　不同供油压力下液压驱动单元力阶跃响应仿真与实验曲线

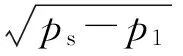
2) 不同正弦力频率下的力控系统特性

设定伺服缸活塞杆初始位置L0=30 mm，系统供油压力ps=7 MPa， 控制器比例增益Kp=5， 给定幅值F=1000 N的正弦力，分别调定给定力频率f=1 Hz、3 Hz和5 Hz时，测试液压驱动单元正弦力响应曲线，并与仿真曲线对比，如图15所示。

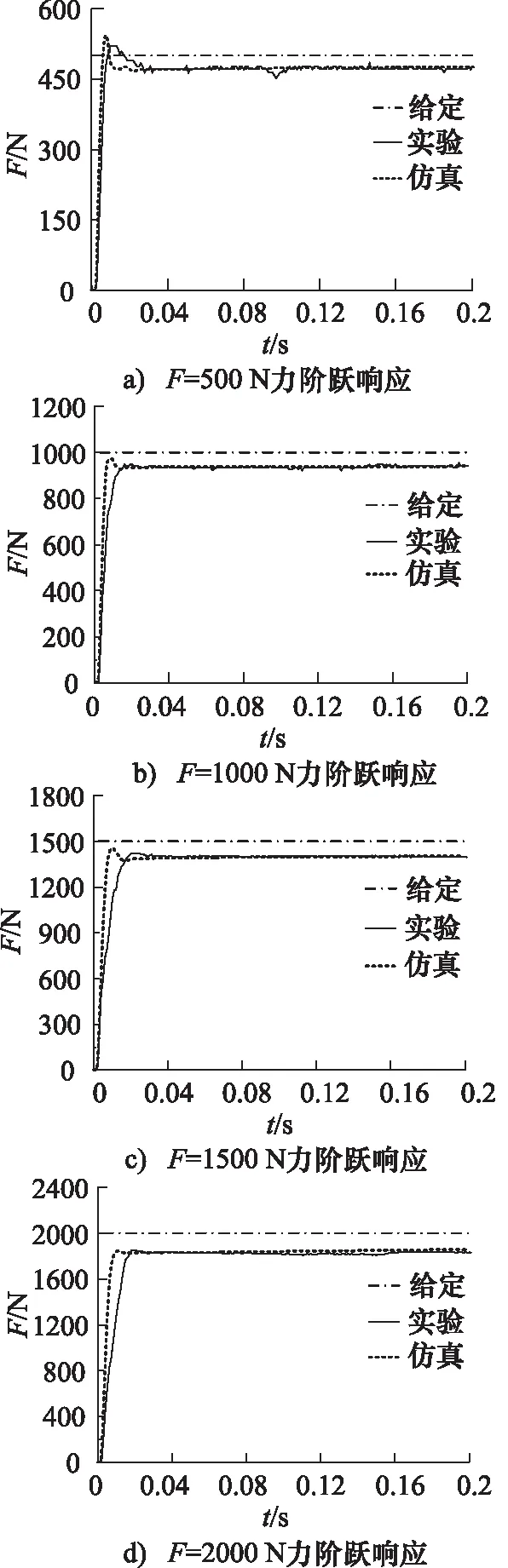
图14　不同阶跃给定力下液压驱动单元力阶跃响应仿真与实验曲线

由图15可以看出，随着给定正弦力频率的提高，力控系统的最大幅值衰减约为2.8%、5.5%和6.7%，相角滞后约为9°、23.4°和28.8°，虽然力控系统的正弦跟踪效果与频率成反比，但在5 Hz时幅值衰减和相角滞后仍均小于10%，可见，液压驱动单元力控系统对于以上频率正弦力的跟踪性能是较好的。

5　结论

本研究针对四足机器人液压驱动单元力控系统进行了数学建模，得到了力控系统传递框图及仿真模型，对不同工作参数和不同给定信号下的液压驱动单元力控性能进行了实验与仿真研究，并得到以下结论：

图15　不同频率正弦给定力下液压驱动单元力阶跃响应仿真与实验曲线

(1) 通过实验和仿真曲线的对比，验证了采用机理建模方法建立的含伺服阀动态和非线性环节的力控系统仿真模型是较为准确的，仿真曲线虽与实验曲线略有偏差，但其定性的分析结果与实验结果吻合；

(2) 控制器比例增益、系统供油压力、力给定的阶跃量均会通过直接或间接地改变力控系统的前向通道增益，进而在一定程度上影响力控系统的性能；

(3) 液压驱动单元在幅值1000 N、5 Hz的正弦给定下，仍能保证其幅值衰减和相角滞后均在10%以内，说明液压驱动单元可以应用于5 Hz频率内的机器人关节力控制。若希望其具备更好的力控性能，有待开展进一步的高性能力控方法研究。

参考文献：

[1]孔祥东，俞滨，权凌霄，等.四足机器人对角小跑步态下液压驱动单元位置控制特性参数灵敏度研究[J].机器人,2015,37(1):53-62.

[2]王立鹏，王军政，汪首坤，等．液压驱动的四足机器人控制系统研究[J]．液压与气动，2011,(1)：29-31.

[3]孔祥东，俞滨，权凌霄，等.四足仿生机器人液压驱动单元轨迹灵敏度分析[J].机械工程学报,2013,49(14):170-175.

[4]丁良宏，王润孝，冯华山，等．浅析BigDog四足仿生机器人[J]．中国机械工程，2012,(5)：505-514.

[5]Singh H P,Sukavanam N.Stability Analysis of Robust Adaptive Hybrid Position/Force Controller for Robot Manipulator Using Neural Network with Uncertainties[J].Neural Computing and Applications,2013,22(7):1745-1755.

[6]周波,钱堃,马旭东,等.移动机器人滑动参数定界及鲁棒镇定控制[J].控制理论与应用,2013,30(5):611-617.

[7]Salisbury J K.Active Stiffness Control of a Manipulator in Cartesian Coordinates[C]. IEEE Conf of Decision and Control. Nov. 1980.pp:95-106. Dept. of Computer Science, Stanford University.

[8]李正义,唐小琦,熊烁,等.卡尔曼状态观测器在机器人力控制中的应用[J].华中科技大学学报(自然科学版)，2012,(2):1-4.

[9]Namvar M, Aghili F. Adaptive Force Control of Robots in Presence of Uncertainty in Enviroment[C]. Proceedings of the 2006 American Control Conference Minneapolis, Minnesota, USA, June 14-16, 2006：3253-3258.