比例电磁铁动态实验与建模仿真

　， ， ， 　(浙江大学 流体动力与机电系统国家重点实验室， 浙江 杭州　310000)

引言

电液比例阀由于具有对油质要求不高、价格低廉、控制性能好的优点，被广泛用于液压系统中。比例电磁铁作为电液比例阀的关键部件，是电液比例阀应用最多的电机械转换器，其功能是将输入的电流信号，转换成力和位移信号输出。

建立准确的电磁铁模型，对分析研究电液比例阀的控制方法起到了关键作用。由于电磁铁存在如磁饱和、磁滞、涡流等诸多非线性因素，建立电磁铁的准确模型具有一定复杂性。常见的建模方法有有限元分析法[1,2]，把电磁铁看成黑箱的系统辨识方法[3]，分析电磁铁磁滞、涡流等电气特性的物理建模方法等[4,5]。

通过简单的实验电路，采集电磁铁阶跃响应的电压、电流、输出力信号。通过将电磁铁模型简化为电阻与非线性电感串联形式，优化等效电阻，得到了满足模型参数拟合要求的电磁铁磁滞回线，并以此为基础进行了模型的拟合。

1　电磁铁实验平台

图1为电磁铁的力特性测试平台[6]。测试平台由压力传感器、位移调整机构、位移测量千分尺组成。位移调整机构用于调整电磁铁的输出位移，以便测量不同位移下电磁铁的输出特性。位移的数值可由千分尺读出。

图2为电磁铁信号采集电路。电路中的二极管在供电断开后起卸荷作用。电路中采用双刀单掷开关，用以避免断电后电源信号对采样信号的干扰。此采样电路能产生较好的阶跃供电信号，并且供电为电源直接供电，驱动能力强。实验时采集电磁铁两端电压VS，压力传感器输出的电压信号F，采样电阻两端电压Vi，并记录千分尺的位移值x。采样电阻两端电压Vi除以采样电阻值RS，得到流过电磁铁的电流值i。

图1　电磁铁力特性测试平台

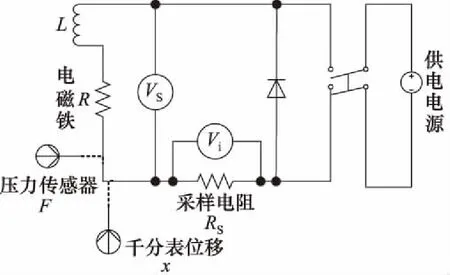
图2　电磁铁信号采集电路

2　电磁铁模型

电磁铁模型可以简化为电阻与电感串联的形式。由于电磁铁工作过程中的涡流效应与铁芯磁性材料的磁滞效应[5]，电感是非线性的[7]。电磁铁两端电压Vs可以分解为：

Vs=VR+VL

(1)

其中,VR为通过电磁铁等效电阻的电压;VL为通过等效电感的电压。设λ为通过电感的磁通量，由电磁感应定律有：

(2)

电磁铁的i-λ曲线存在磁滞现象。可以将电流i看成由两部份组成，一部份为存储在电感中的电能ir，另一部份为涡流效应与磁滞效应消耗的电能id[8,9]，如图3所示。i,ir,id之间的关系式可以表达如下，其中ir=f(λ),id=g(VL)。

i=ir+id=f(λ)+g(VL)

(3)

电磁铁输出力F是与λ2相关的函数，可以写为:

F=h(λ2)

(4)

图3　电磁铁磁化曲线

综上所述电磁铁的模型可以表示为如图4所示的形式。

图4　电磁铁模型

3　实验数据处理与分析

在不同的铁芯位移与输入电压下，通过实验测得通过电磁铁两端的电压VS，通过电磁铁的电流i，电磁铁输出力F，电磁铁铁芯位移x。

如图5所示为电磁铁阶跃响应的电压VS和电流i曲线。图中VS在开始时略有下降是由于供电的输出负载引起的[7]。根据阶跃响应中间段趋于平稳时的信号VS′,i′得到电磁铁的等效电阻。

(5)

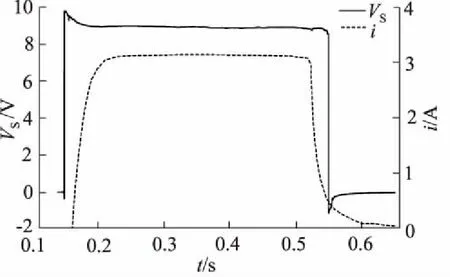
图5　电磁铁阶跃响应VS,i信号

电磁铁等效电感电压VL，通过电磁铁的磁通量λ采用如下公式计算：

VL=VS-iR

(6)

(7)

由于电阻与电感串联形式的简化电磁铁模型，并不是电磁铁的真实模型。因此在按照式(6)、式(7)计算λ，并绘出i-λ曲线后，曲线的末端处有交叉区域，如图6所示。这不符合磁滞回线的实际情况，因此需要调整电阻值R，以使i-λ曲线末端刚好不出现交叉。

图6　不同等效电阻值下i-λ曲线

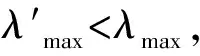
采用优化后的电阻值R通过式(6)、式(7)计算λ，然后通过i-λ曲线计算ir。ir为相同λ值对应的i值的平均值。id用如下公式计算:

id=i-ir

(8)

通过以上过程计算得到实验数据λ,ir,id，绘制实验数据图如图7所示。

图7　不同位移下λ-ir曲线

图7图8为铁芯位移在-0.3 mm, 0.2 mm, 0.7 mm, 1.2 mm,1.7 mm下的λ-ir曲线与F-λ曲线。由图可知，λ-ir,F-λ关系与电磁铁的电芯位移相关，从而式(3)、式(4)可以改写为：

i=ir+id=f(λ,x)+g(VL)

(9)

F=h(λ2,x)

(10)

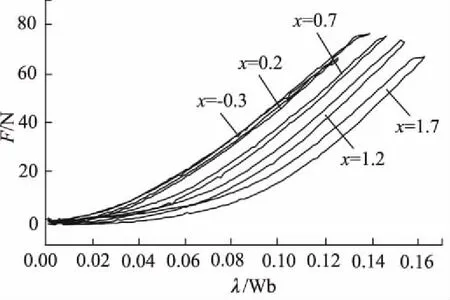
图8　不同位移下λ-F曲线

由图9可知，VL,id的变化趋势是一致的，但存在一个时间上的相位差。VL,id关系式可以修正如下[7,10]，其中τ为时间常数，反应了VL,id之间的相位差：

(11)

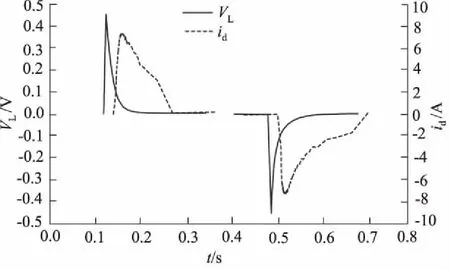
图9　VL, id的时间变化曲线

VL,id的具体关系可以用式(12)的一阶系统近似表达，KP,TP为一阶系统参数。

(12)

综上所述电磁铁的模型可以修改为如图10所示的形式。

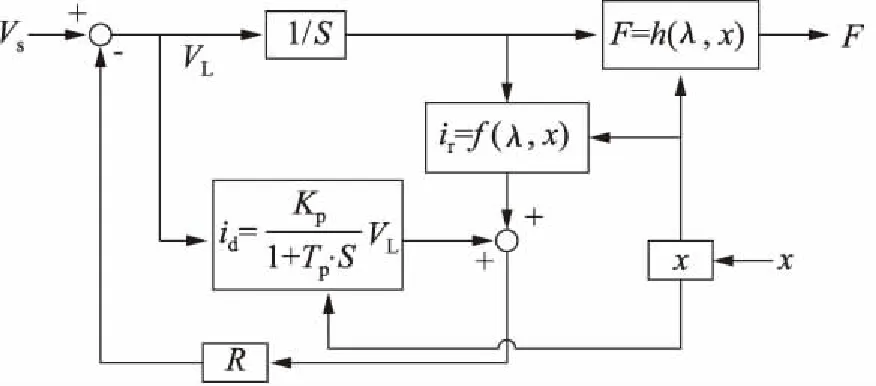
图10　电磁铁模型

4　电磁铁模型参数拟合与仿真结果

根据实验数据，对公式ir=f(λ,x),id=G(S)VL,F=h(λ2,x)的参数进行拟合。

ir=f(λ,x)参数采用多项式拟合的方式确定，其具体形式如下：

ir=f(λ)=f3λ3+f2λ2+f1λ

(13)

其中,

f1=f14x4+f13x3+f12x2+f11x1+f10

f2=f24x4+f23x3+f22x2+f21x1+f20

f3=f34x4+f33x3+f32x2+f31x1+f30

(14)

采用MATLAB系统辨识工具箱的idproc()函数，设定函数参数为P1D模式，对id=G(S)VL进行参数拟合，得到不同位移下的一阶系统参数KP,TP。对不同位移下的KP,TP进行多项式拟合，具体形式如下：

KP=k14x4+k13x3+k12x2+k11x1+k10

TP=k24x4+k23x3+k22x2+k21x1+k20

(15)

F=h(λ2,x) 参数采用多项式拟合的方式确定，其具体形式如下：

F=h3λ6+h2λ4+h1λ2

(16)

其中,

h1=h14x4+h13x3+h12x2+h11x+h10

h2=h24x4+h23x3+h22x2+h21x+h20

h3=h34x4+h33x3+h32x2+h31x+h30

(17)

根据实验数据，拟合后的参数如表1所示。

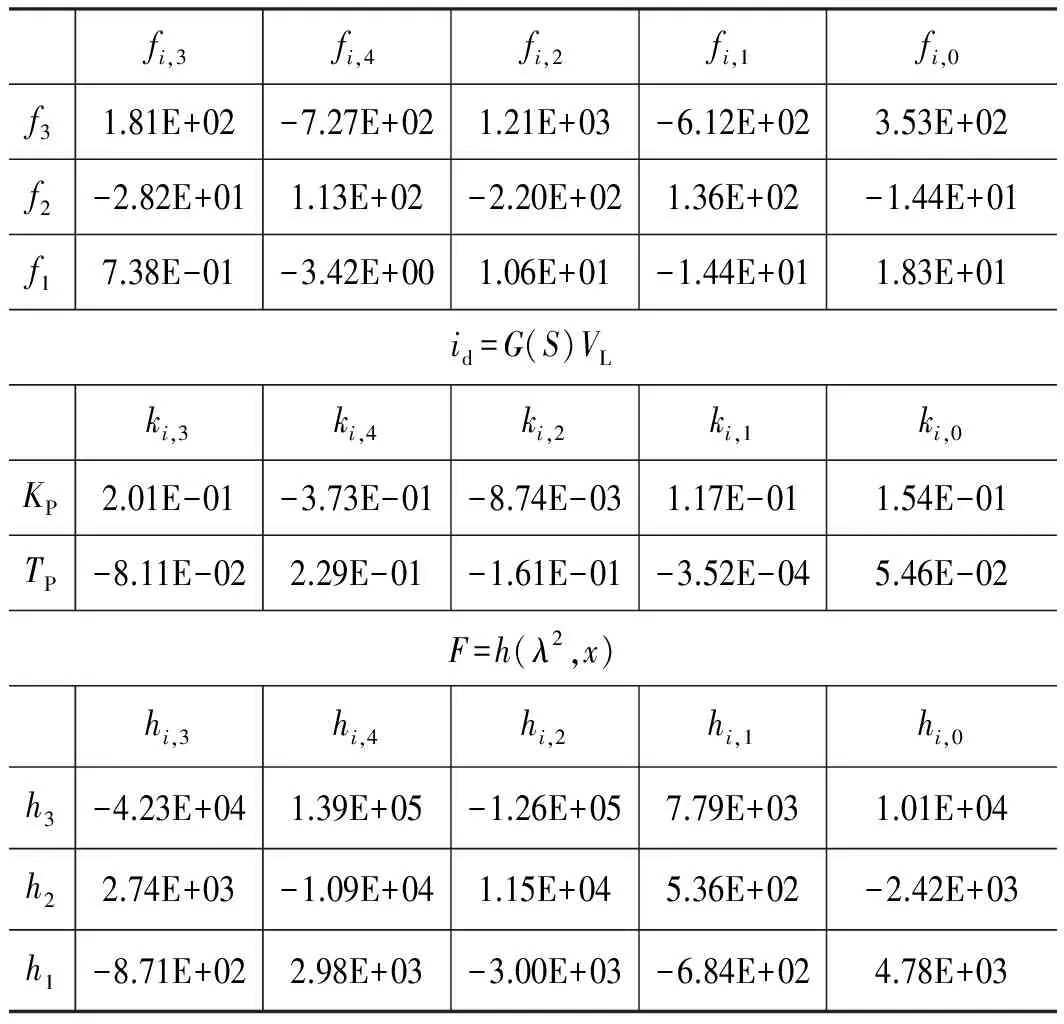
表1　拟合参数数值ir=f(λ,x)

图11、图12为供电压为10 V时，铁芯位移在0.2 mm, 1.7 mm处的i-λ,i-F曲线，虚线为仿真结果，实线为实验结果。由图可以看出，仿真结果总体上能较好的与实验结果相匹配。

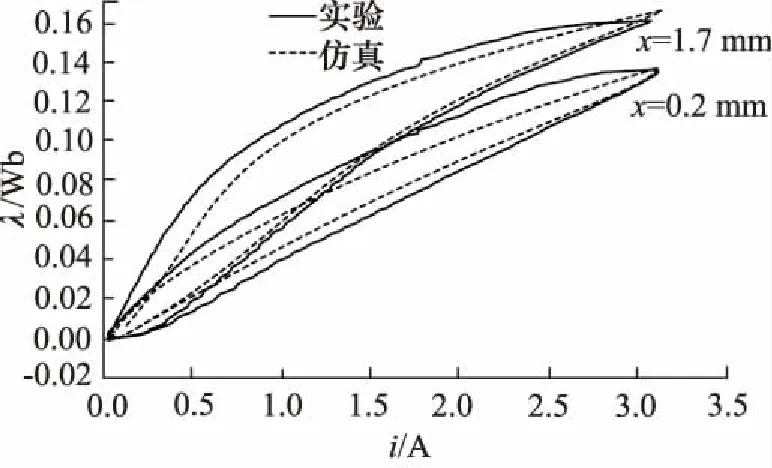
图11　铁芯0.2 mm, 1.7 mm位移处实验与仿真i-λ曲线

图12　铁芯0.2 mm, 1.7 mm位移处实验与仿真i-F曲线

5　结论

通过电磁铁特性测试平台，采用简单的实验测试电路，完成了电磁铁动态阶跃响应的数据采集工作。在将电磁铁简化为电阻与非线性电感的串联模型的理论基础上，处理实验数据得到了电磁铁磁滞回线。通过优化等效电阻的方式，以使磁滞回线能满足模型拟合要求。参数拟合过程中，提出了将等效电感电压VL与耗散电流id之间的关系，简化为一阶系统的方法。这一方法避免了对VL,id关联的时间参数τ的估计[2,7]，简化了模型拟合的过程。仿真结果表明本研究所采用的电磁铁建模方法具有一定实用性。

参考文献：

[1]黄松.比例电磁铁力特性的有限元分析[D].武汉：武汉科技大学,2012.

[2]Cristofori D, Vacca A. The Modeling of Electrohydraulic Proportional Valves[J]. Journal of Dynamic Systems, Measurement, and Control,2012,134(2):021008.

[3]Cincotti S, Marchesi M, Serri A. A Neural Network Model of Parametric Nonlinear Hysteretic Inductors[J]. Magnetics, IEEE Transactions on,1998,34(5):3040-3043.

[4]Jiles D C, Thoelke J B, Devine M K. Numerical Determination of Hysteresis Parameters for the Modeling of Magnetic Properties Using the Theory of Ferromagnetic Hysteresis[J]. Magnetics, IEEE Transactions on, 1992, 28(1): 27-35.

[5]MANDACHE L, TOPAN D, SIRBU I G. Accurate Time-domain Simulation of Nonlinear Inductors Including Hysteresis and Eddy-current Effects[C]//Proceedings of the World Congress on Engineering,2011, 2.

[6]李勇, 丁凡, 李其朋, 等. 电磁铁力特性测试系统的研究[J]. 传感技术学报,2008,(10):2353-2356.

[7]Vaughan N D, Gamble J B. The Modeling and Simulation of a Proportional Solenoid Valve[J]. Journal of Dynamic Systems, Measurement, and Control,1996,118(1):120-125.

[8]Jiles D C, Atherton D L. Theory of Ferromagnetic Hysteresis[J]. Journal of Magnetism and Magnetic Materials,1986,61(1):48-60.

[9]Chua L O, Stromsmoe K A. Lumped-circuit Models for Nonlinear Inductors Exhibiting Hysteresis Loops[J]. Circuit Theory, IEEE Transactions on, 1970,17(4):564-574.

[10]Chua L, Bass S C. A Generalized Hysteresis Model[J]. Circuit Theory, IEEE Transactions on,1972,19(1):36-48.