引入补偿刚度的流体力学标准伽辽金有限元研究

袁行飞，方少文，钱若军

（1.浙江大学 空间结构研究中心，浙江 杭州310058；2.同济大学 土木工程学院，上海200092）

流体力学有限元法是流体力学数值计算中的一种重要方法，其主要是采用了标准伽辽金有限元格式，并且采用了传统的多项式插值函数来得到形函数.由于流体Navier-Stokes方程的解析解至今无法得到，不少学者对简单的一维对流扩散方程进行研究，将一维对流扩散方程蜕化为常系数微分方程，以常微分方程的有限元解与解析解对比，发现了有限元解的波动［1-2］.从某种意义上说，流体力学有限元法的发展过程也是如何解决数值波动的过程，很多方法都是围绕着解的波动问题提出的.国内外学者对流体力学有限元法进行了长期研究，并取得了丰硕成果，如美国麻省理工学院教授 Klaus-Jürgen Bathe领导的研究小组提出的基于流动条件的插值方法（flow-condition-based interpolation，FCBI）已广泛应用于土木、机械等领域［3-5］.英国Swansea大学以Zienkiewicz教授为首的研究小组提出的基于特 征 线 的 分 裂 算 法 （Characteristic-Based Split，CBS）［6-7］现在也已得到了较为广泛的应用.Heinrich和Zienkiewicz等人在1976年提出的迎风有限元法，经过不断的修正和发展，现在已应用到三维流体力学的计算［8-10］.国内较早对流体力学有限元法展开系统研究的学者有章本照［11］、刘希云［12］、杨曜根［13］等.

本文对一维定常对流扩散方程标准伽辽金有限元解的波动问题进行了研究，指出除单元内插值函数连续性差外，单元间形函数一阶导数不连续，即属于不同单元同一节点的左右一阶导数不相等是导致有限元解波动的另一主要原因.进而提出采用补偿标准伽辽金有限元进行分析，通过在单元与单元之间的节点上增加一个“不平衡力”，即在单元间引入补偿项来提高单元间形函数一阶导数的连续性，来减少数值波动.针对线性拉格朗日插值和指数型插值分别探讨了补偿项中补偿刚度表达式，研究了不同修正系数下有限元解的波动情况，确定了最优修正系数.以常见流体为例对比了采用指数型插值函数的补偿标准伽辽金有限元解与解析解计算结果，验证了其有效性.本文工作可为进一步研究和发展三维流体力学有限元法提供思路.

1 一维对流扩散方程的有限元解波动

1.1 解析解

对于在L内定义，待求未知变量为φ的一维定常对流扩散方程

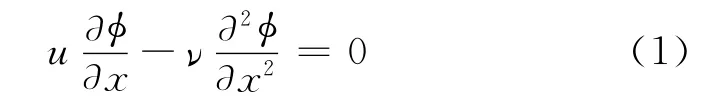
式中：ν为运动黏性系数；u为速度；φ为因变量；x为坐标，0≤x≤L.

式（1）是变系数偏微分方程，通常难以求解.作为问题的近似，假设u为常数，则式（1）蜕化为常系数微分方程.解该方程得

式中：D1，D2均为待定常数，通过引入边界条件φ|x=0=φ0和φ|x=L=φL可惟一确定.式（1）的解析解为

1.2 常用有限元解

现采用标准伽辽金有限元进行求解.首先对定义域L进行剖分，共划分J个线单元，单元长度为Δx，Δx=L／J，则有K（1，2，…，J+1）个节点.采用一维线性拉格朗日插值函数，则式（1）的有限元解为

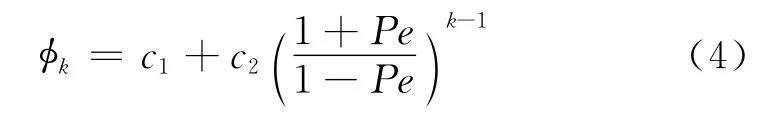
式中：Pe称为贝克莱（Péclet）数，Pe=uΔx／2ν；c1，c2均为待定常数，通过引入边界条件φ|x=0=φj和φ|x=Δx=φj+1可确定.式（1）的有限元解为

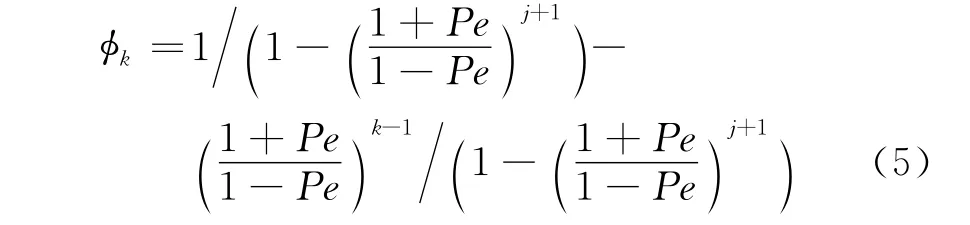
1.3 有限元解波动

取L=1，J=10，ν=0.2，对流速度u分别为0.04和20时，可得相应单元的Pe和φ值.如将每个节点的坐标值代入式（3），则可得到相应的解析解.

图1为该问题的解析解和常用有限元解对比.由图1可见，当Pe较小时，有限元解和解析解十分接近；随着Pe的增加，有限元解与解析解差异逐渐增大.当Pe＞1时，有限元解在解析解附近来回跳动，出现波动现象［2］.

图1 一维对流扩散方程解析解和有限元解对比Fig.1 Comparison of analytical solution and finite element solution

通常将一维对流扩散方程的有限元解产生数值波动原因归纳为：网格的尺寸、对流速度以及黏性系数.已有的解决方法大都针对一维线性拉格朗日插值函数进行研究，提出加密网格、修正运动黏性系数、修正对流速度等方法来改善有限元数值波动.作者认为引起数值波动的两个本质原因是线性拉格朗日插值函数连续性差以及单元之间形函数一阶导数不连续.文献［14］对第一个原因进行了探索，研究结果表明采用连续性较好的插值函数（如三次多项式埃尔米特插值函数、指数型插值函数等）是改善数值波动的有效方法.但这些插值函数仍不能保证节点处不同单元的连续性.以一维问题为例，同一节点属于前后两个单元，前一单元右节点的一阶导数不等于后一单元左节点的一阶导数.为解决这一问题，本文通过引入补偿项来改善单元之间节点处的连续性，从而改善一维对流扩散方程标准伽辽金有限元数值波动，为研究和发展三维流体力学有限元法提供思路.

2 补偿标准伽辽金有限元基本原理

2.1 标准伽辽金有限元格式

方程（1）对流扩散微分方程可写成等价的变分公式，当对此变分公式采用标准伽辽金有限元法求解时，需先给出如下变分公式的弱形式：

采用分部积分，并引入Gauss-Green公式，对含有函数二阶导数的扩散项降阶，得

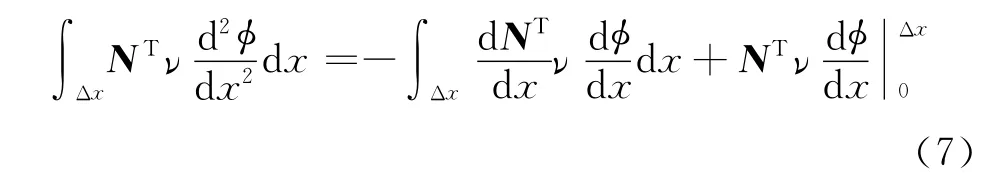
因此一维对流扩散方程的标准伽辽金有限元格式为

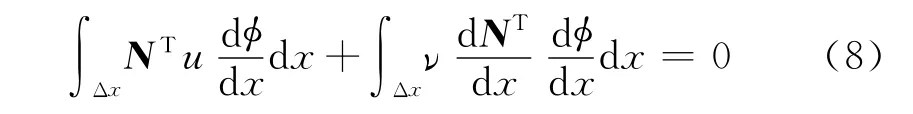
式中：N为单元的形函数；φ=Nφe；φe为函数φ在单元节点处的值.

2.2 补偿有限元基本原理及格式

对一维对流扩散问题的连续性进行分析，发现引起数值波动一个重要的原因是由于单元之间函数的一阶导数不连续.如图2所示，为了提高单元间函数一阶导数的连续性，减小波动，可在单元之间即节点处引入补偿项

式中：λ为补偿刚度，其物理意义类似于固体力学中发生单位转角所需施加的弯矩；dφ／dx为单元间的转角.针对不同的插值函数，补偿刚度λ表达式可以不同.

上述引入补偿项的方法可以不改变原来插值函数，也不会增加单元的自由度及内插点数，而仅在单元与单元之间的节点上增加一个“不平衡力”，从而使得单元之间的连续性得到改善，较好地控制有限元解的波动问题.

图2 单元间的弹性约束Fig.2 Elastic constraint between different elements

引入补偿项后的补偿标准伽辽金有限元格式为

式（10）右端项φe为前一步计算得到的节点值，通过不断的迭代求解，φ最终收敛到较精确的数值解.

3 采用线性拉格朗日插值的补偿标准伽辽金有限元

3.1 线性拉格朗日插值函数

为进行一般性研究，剖分定义域L为J个线单元，单元长度为Δx=L／J，则有K（1，2，…，J+1）个节点.单元内各点的值可用单元节点处值表示

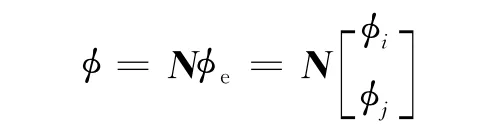
3.2 补偿标准伽辽金有限元补偿刚度

由于单元之间采用的是拉格朗日插值，其一阶导数不连续，导致Pe＞1时有限元解存在较大波动（图1）.为了增强单元间函数一阶导数的连续性，减小波动，考虑在单元之间引入包含补偿刚度λ的补偿项.参考迎风有限元格式［8-10］，初步确定线性拉格朗日插值补偿项中补偿刚度λ的表达式如下：

式中：Pe=uΔx／2ν；k为修正系数.

研究表明，数值波动程度与k值有关.当k值较小时，数值解存在一定程度的波动，随着k值的增加数值波动逐渐减缓；但当k值过大时，数值解又逐渐偏离解析解.为了获得最优的修正系数k，令有限元值与解析解的误差为.其中φi，φ′分别为解析解和采用补偿线性拉格朗日插值的有限元解.

以u=8，L=1，J=10为例，当Pe分别为5和100时，采用不同修正系数k的补偿线性拉格朗日插值有限元解波动情况见图3和图4.

图3 Pe＝5时补偿线性拉格朗日插值有限元解波动Fig.3 Solution wave of CSGFE using LLBI at Pe＝5

由图3，4可以看出，当Pe较大时，线性拉格朗日插值出现了严重的波动现象，而引入补偿项以后，波动情况得到明显改善.对于不同的调整系数k，波动的改善情况有所不同.当k＜1.0时，随着k的增加，补偿线性拉格朗日插值的误差越来越小；k＞1.0时，误差又急剧上升；而当k=1.0时，线性拉格朗日插值的误差最小，可以获得与解析解最为接近的数值解.因此，取k=1.0为补偿线性拉格朗日插值的最优修正系数.此时补偿线性拉格朗日插值能提高单元之间的连续性，改善波动情况，取得较好的数值解.

由此确定采用线性拉格朗日插值的补偿标准伽辽金有限元补偿刚度λ的表达式为

4 采用指数型插值的补偿伽辽金有限元

4.1 指数型插值函数

设有限元解为φ=c1+c2eax，单元形函数为N=.其中a的取值与流场属性有关［14］.取不同a值时指数型插值函数有限元解波动见图5.由图5可见，线性拉格朗日插值有较大波动，指数型插值的波动情况与a值有关.随着a增大，有限元解波动减小.当a=u／v=80时，有限元计算结果与解析解基本一致.

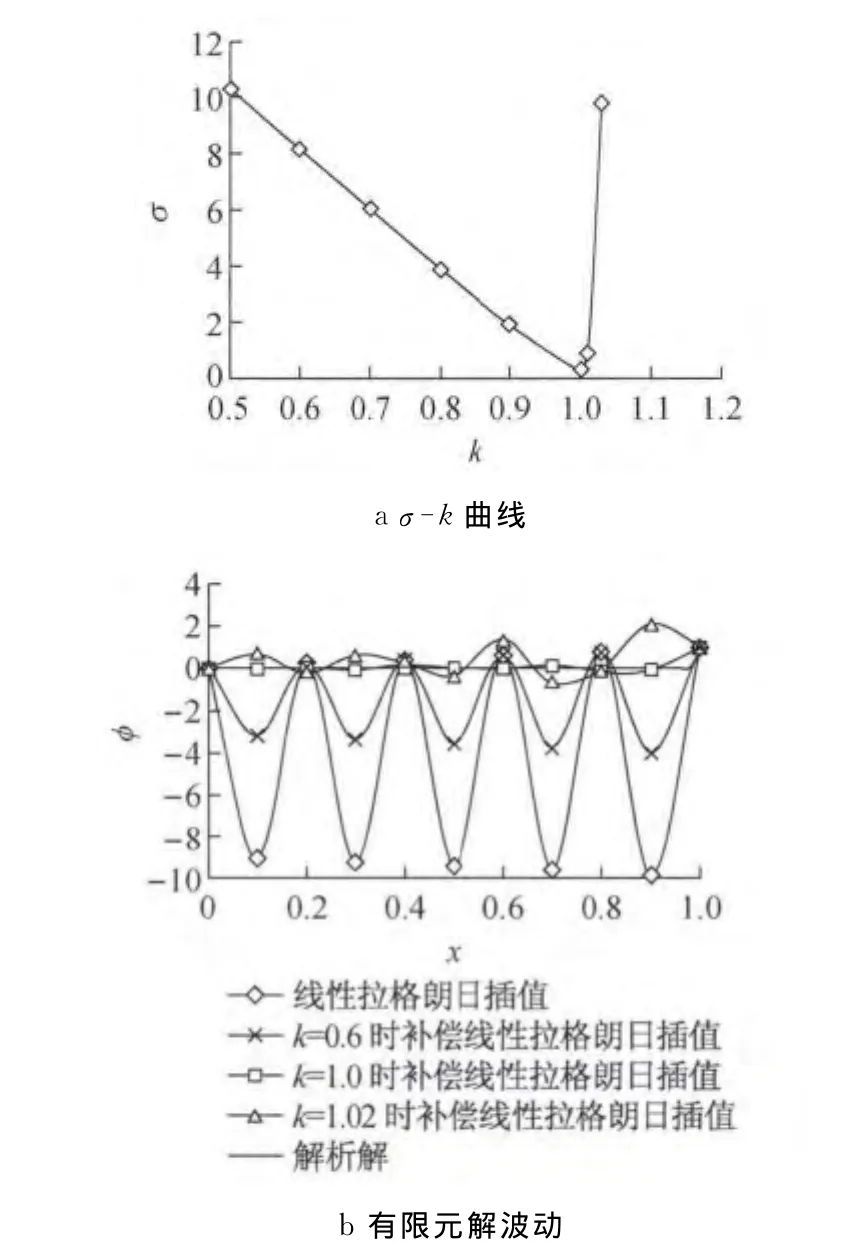
图4 Pe＝100时补偿线性拉格朗日插值有限元解波动Fig.4 Solution wave of CSGFE using LLBI at Pe＝100

图5 不同a值时指数型插值函数有限元解Fig.5 Finite element solution using EFBI with different a

4.2 补偿标准伽辽金有限元补偿刚度

指数插值函数在单元内更光滑，并且多阶连续，因而可以获得问题更好的数值解.但采用不同a值时，指数插值函数仍会出现不同幅度的波动.其原因仍在于单元之间采用的是拉格朗日插值，其一阶导数不连续.同理，为增强单元间函数一阶导数的连续性，考虑在单元之间引入包含补偿刚度的补偿项，建议如下补偿刚度λ的表达式：

式中：Re=φΔx／2ν；k为修正系数.数值波动程度与k取值有关.

以u=5，L=1，J=10为例，当Pe分别为25，2 500时，采用不同修正系数k的补偿指数型插值有限元解波动情况见图6和图7.

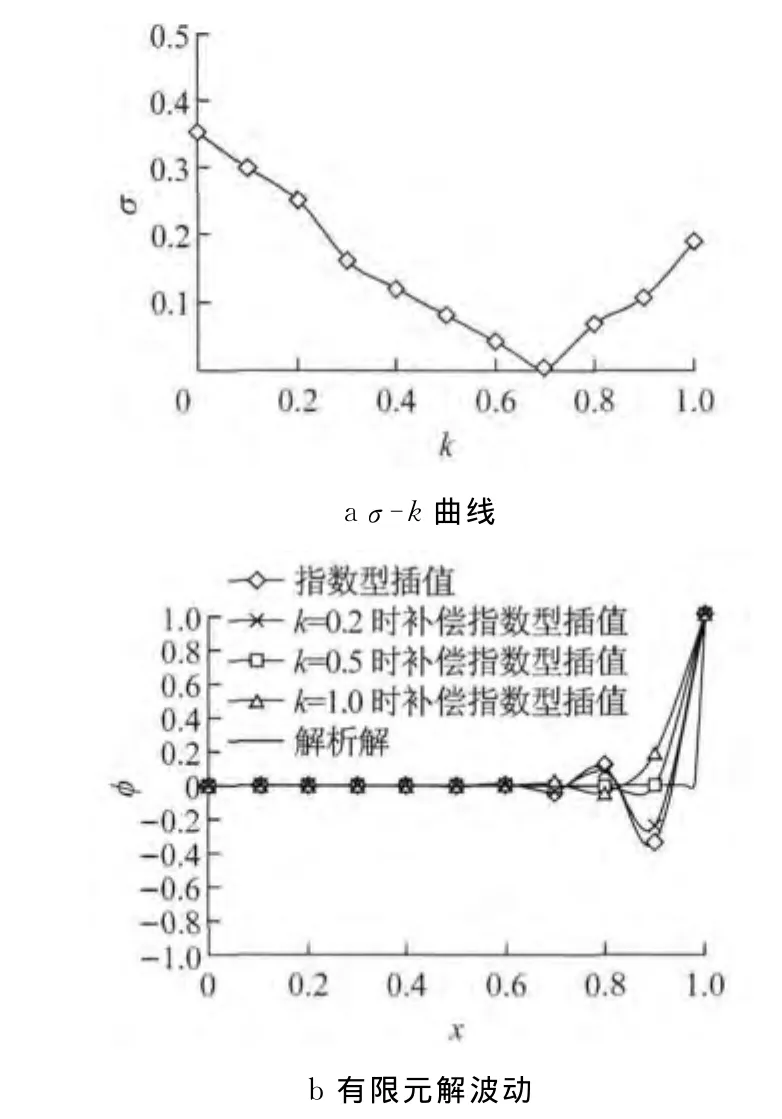
图6 Pe＝25时补偿指数型插值有限元解波动Fig.6 Solution wave of CSGFE using FEBI at Pe＝25

由图6，7可知，与线性拉格朗日插值相比，补偿指数型插值在单元内和单元之间都有较好的连续性，能够较显著改善波动情况，取得较好的数值结果.而对于不同的修正系数，当k＜0.5时，随着k的增加，补偿指数型插值的误差越来越小；当k＞0.5时，误差不断增加；当k=0.5时，补偿指数型插值的误差最小，可以获得与解析解最为接近的数值解.因此取k=0.5为补偿指数型插值的最优修正系数.此时补偿指数型插值能提高单元之间的连续性，改善波动情况，取得较好的数值解.

由此确定采用指数型插值的补偿标准伽辽金有限元补偿刚度λ的表达式为

图7 Pe＝2 500×103时补偿指数型插值有限元解波动Fig.7 Solution wave of CSGFE using FEBI at Pe＝2.5×103

图8 不同流体的补偿指数型插值有限元解波动Fig.8 Solution wave of CSGFE using EBI of different fluids

采用公式（14），当u=10，L=1，J=10时，对常温（27℃）下空气（νa=1.6×10-5m2·s-1）和水（νw=8.6×10-7m2·s-1）两种常见流体的补偿指数型插值有限元解波动进行了研究，结果见图8.由图可知，对于常见流体空气和水，补偿指数型插值均能取得较为理想的结果，与精确解非常接近.

5 结论

（1）本文对一维定常对流扩散方程标准伽辽金有限元解的波动问题进行了研究，指出提高单元内插值函数连续性和单元之间形函数连续性是改善一维对流扩散方程有限元解数值波动问题的有效途径.

（2）本文提出的补偿标准伽辽金有限元在原来插值函数的基础上，不增加单元的自由度及内插点数，只是增加了补偿项，即在单元与单元之间的节点上增加一个“不平衡力”，就可使得单元之间的连续性得到改善，从而更好地控制数值波动现象，取得问题较好的数值解.

（3）相比于常规多项式插值需增加插值函数的阶次来提高计算精度，本文提出的补偿标准伽辽金有限元格式不增加单元的自由度及内插点数，即在不明显增加计算量的前提下使得计算精度得到大幅提高.

（4）本文探讨了采用线性拉格朗日插值和指数型插值的补偿标准伽辽金有限元补偿刚度表达式.相比标准伽辽金有限元，补偿标准伽辽金有限元均能提高单元之间的连续性，显著改善波动情况.

（5）本文研究结果表明采用指数型插值函数的补偿标准伽辽金有限元不仅在单元内可精确给出变量的分布，而且单元之间的连续性更好，因而能更好地控制数值波动现象，取得问题较好的数值解.本文工作可为进一步研究和发展三维流体力学有限元法提供思路.

［1］ Zienkiewicz O C，Taylor R L.The finite element method for fluid dynamics［M］.5th ed.Elsevier：Amsterdam，2000.

［2］ Belytschko T，Liu W K，Moran B.Nonlinear finite elements for continua and structures［M］.New York：John Wiley &Sons Limited，2000.

［3］ Bathe K J.Finite element procedures［M］.New Jersey：Prentice Hall，1996：1-25.

［4］ Bathe K J，ZHANG Hou.A flow-condition-based interpolation finite element procedure for incompressible fluid flows［J］.Computers and Structures，2002，80（14）：1267.

［5］ Kohno H，Bathe K J.A nine-node quadrilateral FCBI element for incompressible fluid flows［J］.Communications in Numerical Methods in Engineering，2006，22（8）：917.

［6］ Zienkiewicz O C， Wu J.A general explicit or semi-explicit algorithm for compressible and incompressible flows ［J］.International Journal for Numerical Methods in Engineering，1992，35（3）：457.

［7］ Nithiarasu P，Codina R，Zienkiewicz O C.The characteristicbased split（CBS）scheme—a unified approach to fluid dynamics［J］.Numerical Methods in Engineering，2006，66（10）：1514.

［8］ Hughes T J R，Brooks A.A theoretical framework for Petrov-Galerkin methods with discontinuous weighting functions：Application to the streamline-upwind procedure［J］.Finite Elements in Fluids，1982，4（2）：47.

［9］ Burman E，Smith G.Analysis of the space semi-discretized SUPG method for transient convection—diffusion equations［J］.Mathematical Models and Methods in Applied Sciences，2011，21（10）：2049.

［10］ Takase S，Kashiyama K，Tanaka S，etal.Space-time SUPG finite element computation of shallow-water flows with moving shorelines［J］.Computational Mechanics，2011，48（3）：293.

［11］ 章本照.流体力学中的有限元方法［M］.北京：机械工业出版社，1986.ZHANG Benzhao.The finite element method in fluid mechanics［M］.Beijing：Mechanical Industry Press，1986.

［12］ 刘希云，赵润祥.流体力学中的有限元与边界元方法［M］.上海：上海交通大学出版社，1993.LIU Xiyun，ZHAO Runxiang.Finite element and boundary element methods in fluid mechanics［M］.Shanghai：Shanghai Jiaotong University Press，1993.

［13］ 杨曜根.流体力学有限元［M］.哈尔滨：哈尔滨工程大学出版社，1995.YANG Yaogen.Fluid dynamics finite element［M］.Harbin ：Harbin Engineering University Press，1995.

［14］ 方少文，袁行飞，钱若军，等.采用不同插值函数的流体力学有限元数值波动研究［J］.工程力学，2013，30（11）：266.FANG Shaowen，YUAN Xingfei，QIAN Ruojun，etal.Numerical wave of finite element solution in fluid mechanics using different interpolation function［J］.Engineering Mechanics，2013，30（11）：266.