基于损伤理论的钢筋混凝土结构裂缝分析

任晓丹，李 杰

（同济大学 土木工程学院，上海200092）

通常情况下，钢筋混凝土构件是带裂缝工作的.如果裂缝的开展超过一定的限值，就会对结构的使用性能产生影响.在某些特殊环境下，比如干湿交替、冻融交替、地下水侵蚀等环境下，裂缝的开展甚至会直接危及结构的安全.所以钢筋混凝土结构的开裂，特别是外力作用下的裂缝开展宽度问题，是钢筋混凝土结构学研究的经典问题，很早就得到了国内外研究者的重视［1-3］.在我国，东南大学、大连理工大学、清华大学等单位的学者对这一问题开展了系统研究［4-6］，产生了一批重要成果，并构成了我国现行规范裂缝宽度计算公式的基础.

近年来，工程实践的发展对裂缝宽度的计算提出了新的要求.首先，高强材料特别是高强钢筋的应用使得钢筋混凝土构件的使用应力提高，进而可能提高裂缝宽度，而经典的裂缝宽度计算公式目前还比较缺乏高强材料构件试验数据的有力支持；其次，随着重大工程结构的兴建以及结构形式的创新，复杂的组合构件大量采用，其裂缝宽度的估计难以基于经典理论进行.另一方面，结构分析理论与数值技术的长足进步则为裂缝宽度的计算开辟了新途径.经过多年的发展［7-9］，损伤力学模型已经成为混凝土本构关系建模与结构非线性分析最为常用的模型之一.基于损伤力学理论与结构非线性有限元分析，有望对钢筋混凝土结构的裂缝宽度给出更加精细的描述.本文即以此为切入点展开研究.

1 混凝土损伤模型简述

在外力作用下，混凝土表现出显著的软化、弱化等力学行为.损伤力学引入损伤变量描述材料的非线性行为，能够兼顾混凝土非线性行为的物理机制和外在表现，所以越来越多地受到研究人员与工程技术人员的关注.本文所采用的损伤模型，在《混凝土结构设计规范（GB 50010-2010）》建议模型［10］的基础上进行了局部调整.

首先考虑单轴本构关系.基于弹性损伤理论，可以将单轴本构关系统一写为如下形式：

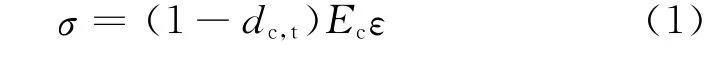
式中：σ与ε分别表示单轴应力与单轴应变；Ec表示混凝土弹性模量；d表示损伤变量，下标c，t表示对应的应力状态，即压应力作用时取受压损伤dc，拉应力作用时取受拉损伤dt.对《混凝土结构设计规范（GB 50010-2010）》建议损伤演化表达式做局部简化调整，可以采用如下统一表达式表示受拉、受压损伤演化：

其中

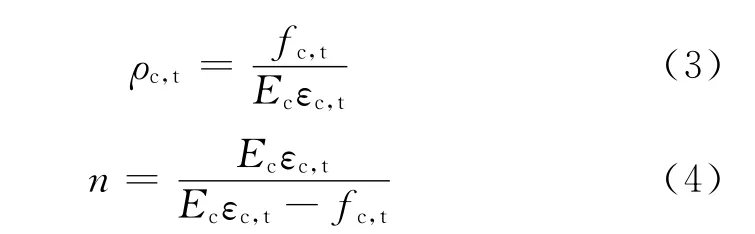
式中：fc，t与εc，t分别为混凝土单轴强度与对应峰值应变代表值，根据受力状态分别取受压（下标c）和受拉（下标t）；αc，t为应力应变曲线下降段参数，对于受压（下标c）和受拉（下标t）分别取不同的数值.

对于双轴应力状态，本构关系应在主应力空间建立.为此，首先定义如下有效应力表达式：

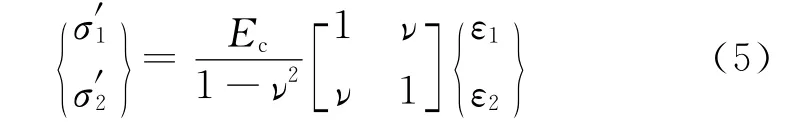
式中：ν为混凝土泊松比；σ′与ε分别为有效应力和应变；下标分别表示第一主方向与第二主方向.

在不同的拉、压应力组合作用下，混凝土的非线性表现有明显差异，须分别加以考虑［11］.

此时只有受拉损伤起作用，本构关系表达式为

受拉损伤演化由如下受拉能量等效应变控制：

将x=εt，e／εt代入式（2）即可求得dt.

此时只有受压损伤起作用，本构关系表达式为

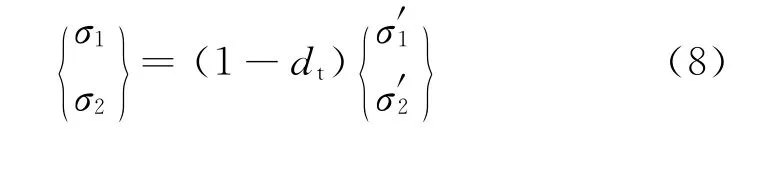
受压损伤演化由如下受压能量等效应变控制：

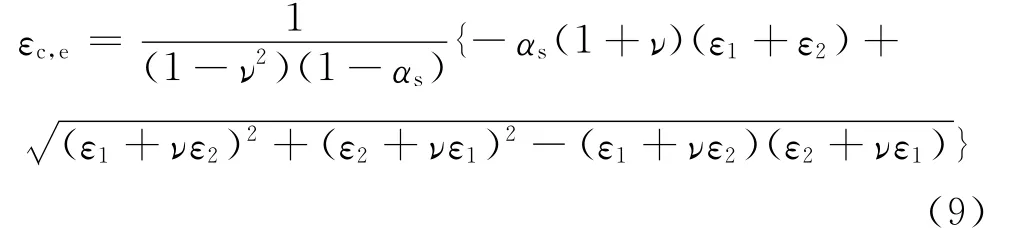
其中双轴受力控制参数αs计算公式为

r为双轴等压时强度提高系数，根据双轴受压结果确定，在缺乏试验结果时，可取1.2.将x=εc，e／εc代入式（2）即可求得dc.

此时受拉、受压损伤均起作用，本构关系表达式为

此时受拉能量等效应变为

将x=εt，e／εt代入式（2）即可求得dt.受压能量等效应变按式（9）求出，将x=εc，e／εc代入式（2）即可求得dc.

需要指出，由于本文只针对单调加载条件下构件的裂缝宽度展开研究，不考虑重复加载或者反复加载的情形，所以上述本构关系表达式中未考虑卸载段以及残余应变的影响.

2 裂缝宽度计算

裂缝宽度具有长度的量纲，所以其计算和分析必然要联系到构件及其数值分析模型的内蕴长度量.对于裂缝宽度问题，最重要的内蕴长度量是裂缝间距，一般用lm表示.裂缝间距实际上综合反映了钢筋变形、混凝土强度、钢筋与混凝土之间的黏结滑移等因素的综合作用，并最终以长度的形式体现出来.经典的钢筋混凝土结构理论在大量试验的基础上，提出了描述裂纹间距的黏结滑移理论和无滑移理论.而我国规范中采用的裂纹间距公式则综合了黏结滑移理论与无滑移理论.在裂缝间距基础上，传统混凝土结构理论借助受拉区混凝土与钢筋的变形差计算其裂缝宽度.

引入损伤力学理论和非线性有限元分析方法，可以较为准确地得到钢筋混凝土构件的应力、应变、位移等状态变量以及损伤的分布.但是，由于损伤力学理论采用刚度连续退化的形式考虑裂缝开展对混凝土材料行为的影响；而非线性有限元则将裂纹开展的变形弥散到单元的总变形中，以平均应变的形式表示.所以基于上述理论得到的分析结果中并不直接包含裂缝的信息.

为从连续的应变场与损伤场中解析出裂缝开展的信息，首先考察带裂缝单元的应变，有如下公式：

式中：ε为考虑裂缝开展之后单元的宏观（平均）应变；εe为未开裂部分材料的应变，不妨认为未开裂材料还保持弹性，其表达式为

结合前述理论，考虑受拉损伤，可进一步得到

定义wf为开裂引起的单元附加变形，可得

其中lE为单元的等效长度.将式（16）代入式（17），可得

其中

定义为单元的总变形.若一个单元中只包含一条裂缝，那么根据式（18）求得的wf即为裂缝宽度.对于混凝土构件分析，当采用较为细致的网格划分时，假定一个单元中最多仅允许出现一条裂缝是合理的.

对于大型复杂结构，为了平衡计算成本与计算精度，网格划分往往比较粗.此时构件局部的应力等结果往往不甚准确.若此时仍然希望对构件的局部开裂情况作粗略估计，就需要事先假定多条裂纹在单元内部的分布情况.为了分析方便，这里假定同一单元中的Nf条裂纹同时出现，并且开裂宽度一致，均为w，可得

需要指出的是，对于一个单元内包含多条裂缝的情况，式（20）所给出的假定是十分简化的，仅能在工程应用的角度对局部裂缝情况作粗略估计.更加精细的分析模型应当考虑单元中不同裂缝的相互作用.

将式（20）代入式（18）并化简，最终得

采用max表示状态量在整个加载过程中的最大值，那么最大裂缝宽度

而

为加载过程中曾达到的最大单元变形；Nf，max为对应于最大应变发生时刻单元中的裂纹条数，结合裂缝间距lm的定义，可得

式（24）中第一种情况取1，表示只要单元产生了损伤，就认为其中至少有一条裂缝开展；第二种情况没有取整数，是考虑裂纹开展的位置不同将导致相同长度的单元所能容纳的裂纹条数不同.将式（24）代入式（22）并化简，得

上述裂缝宽度公式的推导是基于一维受力状态，对于多维受力状态，单元的应变ε不再是一个标量，不能直接代入公式（23）计算wE，max.为了避免多维应力及应变分析的复杂性，本文建议基于最大能量等效应变求取最大裂缝宽度，有

式中

为加载过程中曾达到的最大受拉能量等效应变，受拉能量等效应变可根据不同的应力状态采用式（7）或（12）计算.

由上述分析可以看出，损伤演化是裂缝开展的基础.对于计算公式中出现的两种情况，可以理解为：如果单元尺寸lE小于裂缝间距lm，一个单元中最多有一条裂缝，裂缝张开位移引起的附加应变εf应该在单元尺度范围内做平均；而当单元尺寸lE大于裂缝间距lm，那么一个单元中包含多条裂缝，裂缝张开位移引起的附加应变εf需要在裂缝间距范围内做平均.

求解裂缝间距lm可考虑如下途径：对于以正截面破坏控制的梁柱构件，lm可根据《混凝土结构设计规范（GB 50010-2010）》建议公式估计；对于复杂受力构件，lm的求解宜根据精细数值模拟的结果求得.由局部构件的精细有限元分析结果得到裂缝间距lm，进而应用于宏观尺度结构的分析方法，是典型的多尺度分析思路，值得更加深入地研究.

对于单元等效长度，可采用下面公式进行估算［3］：

式中：nd为单元的维数；md为单元的体积量度，一维单元为长度，二维单元为面积，三维单元为体积.

3 算例与验证

3.1 弯曲裂缝宽度计算

采用Harris等人近期发表的高强混凝土梁试验结果［12］作为本文模型的验证.试验梁如图1所示，图中P为外荷载，梁高度h=406mm，宽度b=305 mm，实测混凝土圆柱体抗压强度f′c=89MPa，实测钢筋屈服强度fy=898MPa，实测受力主筋保护层厚度为47mm.计算中还需要另外一些材料参数取值，由于原文中没有直接测量，本文根据材料实测强度等信息取如下数值：混凝土弹性模量Ec=35 GPa，混凝土泊松比ν=0.2，混凝土抗拉强度ft=5.0MPa，混凝土受拉峰值应变0.000 15，混凝土受压峰值应变0.002 5，受拉下降段参数αt=1.0，受压下降段参数αc=2.0，钢筋弹性模量Es=200GPa.

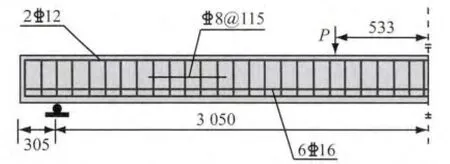
图1 高强混凝土梁配筋图（单位：mm）Fig.1 Details of RC flexural beam（unit：mm）

根据上述信息，基于软件ABAQUS有限元计算平台建立有限元模型，混凝土采用三维8节点实体单元，钢筋采用杆单元，将钢筋直接埋入混凝土并考虑二者变形一致，钢筋采用理想弹塑性本构关系，混凝土损伤本构关系以用户自定义材料的形式植入到有限元模拟平台中进行有限元模拟.

所得力-位移曲线如图2所示.图中荷载数值为一个加载支座上的荷载，梁上的总荷载是图示荷载的2倍.可见模拟结果能够很好地反映从钢筋混凝土加载到破坏的各个阶段的特点，并且与试验结果有一定的吻合度.由于试验的目的是使用阶段的裂缝测量，所以试验中并没有将梁加载至破坏.根据《规范》［10］公式，可计算得到梁的破坏荷载为142 kN，而数值模拟所得力-位移曲线的峰值为144kN，二者符合很好.

图2 力-位移曲线Fig.2 Load-displacement

图3 弯曲裂缝宽度-荷载曲线Fig.3 Load versus crack

图4 计算弯曲裂缝分布图Fig.4 Distribution of flexural cracks

采用本文模型计算弯曲裂缝宽度，与实测结果以及《规范》公式结果共同绘制于图3中.可以看出，三者的符合程度很好，由此初步验证了本文模型的正确性.对于使用荷载作用下受弯构件的最大裂缝宽度，不论是本文提出方法还是《规范》公式，均可以给出具有较高精度的结果.而由于结合了有限元方法，本文模型还可以给出更加精细的结果.图4即为按照有限元分析结果描画出的裂缝分布图.图中，Pu为极限外荷载，实线为达到或者接近最大裂缝宽度的主裂缝，虚线为开展宽度相对主裂缝较小的裂缝.通过裂缝分布图，可以清楚地辨识裂缝的分布规律与最大裂缝宽度发生的位置.另外，构件破坏阶段的裂缝宽度以及裂缝扩展规律，也可以直接基于本文模型的分析结果得到，见图3.

3.2 剪切裂缝宽度计算

钢筋混凝土梁抗剪强度与受剪裂缝的预测问题是钢筋混凝土结构理论的经典难题，至今没有很好解决.将损伤理论与非线性有限元方法相结合，可以为构件抗剪强度以及受剪非线性行为的预测开辟新的道路.本文提出的裂缝宽度模型同样适用于剪切型裂缝的开展宽度预测.

基于湖南大学沈蒲生教授课题组的试验结果［13］验证本文模型.试验梁的加载与配筋情况如图5所示，梁高h=300mm，梁宽b=150mm，实测混凝土立方体抗压强度fcu=51MPa，实测混凝土抗拉强度ft=2.92MPa，实测钢筋屈服强度fy=547MPa，实测纵向钢筋保护层厚度为35mm.根据实测材料强度，分析中其他参数取值为：混凝土弹性模量Ec=30 GPa，混凝土泊松比ν=0.2，混凝土棱柱体抗压强度按照经典换算公式得fc=0.76fcu=39MPa，混凝土受拉峰值应变为0.000 12，混凝土受压峰值应变为0.002，受拉下降段参数αt=0.5，受压下降段参数αc=2.0，钢筋弹性模量Es=200GPa.

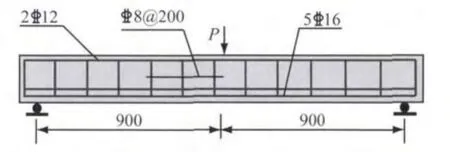
图5 混凝土梁配筋图（单位：mm）Fig.5 Details of RC shear beam（unit：mm）

基于软件ABAQUS建立上述试验梁的有限元分析模型，为了模拟斜裂缝开展，混凝土采用三维5面体（楔形）单元，钢筋仍采用杆单元并埋入混凝土中；钢筋采用理想弹塑性本构关系，混凝土采用损伤本构关系，基于用户自定义材料植入有限元计算平台中.

图6给出了模拟所得力-位移曲线与试验结果的对比.图中，V为剪力，Vu为极限剪力.由图可以看出，基于损伤模型的非线性有限元分析结果与试验结果有很好的吻合度，模拟所得抗剪承载力（122 kN）略小于试验测得抗剪承载力（132kN）.基于本文提出的方法，在有限元分析的过程中同时求解了构件的（剪切）裂缝宽度，并与试验结果进行了对比（图7）.图中同时给出了按照赵国藩模型［5］和聂建国模型［6］计算所得剪切裂缝宽度结果.由图中结果可以看出，本文模型能够较为准确地追踪裂缝开展的全过程，所得结果与试验结果符合较好.即便试件进入临近破坏的阶段，本文方法依然能给出较为准确的结果.除了使用荷载阶段的最大裂缝宽度，本文方法还能精细地给出构件中斜裂缝产生与扩展的过程.图8即为根据有限元分析结果描画出的裂纹分布图.图中，实线为达到或者接近最大裂缝宽度的主裂缝，虚线为开展宽度相对主裂缝较小的裂缝.

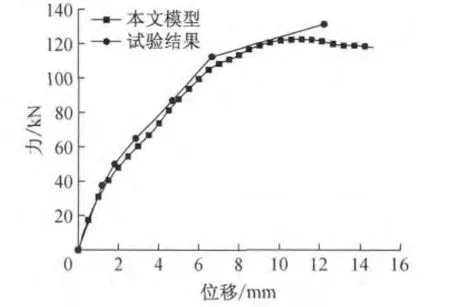
图6 力-位移曲线Fig.6 Load-displacement

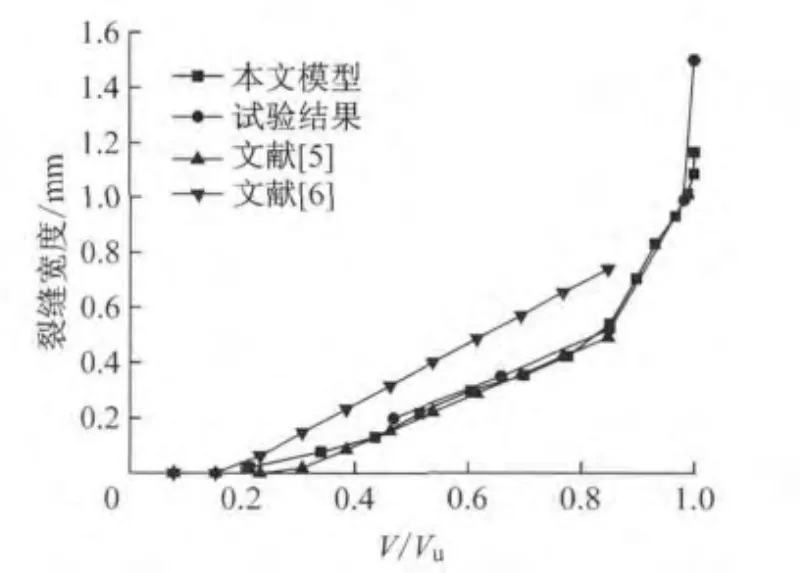
图7 剪切裂缝宽度-相对荷载曲线Fig.7 Normalized load versus crack width

4 结论与讨论

基于损伤力学模型提出了钢筋混凝土构件裂缝宽度的计算方法，结合试验结果进行了验证.根据本文研究，可以得到如下结论：

（1）混凝土的损伤与裂缝开展直接相关，本文所得裂缝宽度表达式具有一定的普遍性，适用于受弯、受剪等构件受力状态，且适用于初始开裂阶段直至后续破坏全过程分析.

（2）分析结果与试验结果的对比表明，基于损伤力学理论建立的裂缝宽度表达式可以较为精确地计算钢筋混凝土构件的裂缝宽度.对于对开裂敏感的结构，如地下室、大型容器以及大坝等，本文方法提供了较为精细的分析工具.

图8 计算剪切裂缝分布图Fig.8 Distribution of flexural cracks

（3）现行混凝土结构设计规范建议的混凝土本构关系，其基础是素混凝土的试验结果.在配置了钢筋之后，二者的相互作用会使混凝土的非线性行为有一些变化，其中最典型的就是钢筋混凝土中混凝土应力应变关系的下降段较之素混凝土更加平缓.这将对构件和结构的行为产生一定的影响，计算中应该予以考虑.本文初步采用适当减小下降段参数αc，t的方式加以考虑.针对这一问题，还需要进一步开展系统的研究.

［1］ Broms B B.Crack width and crack spacing in reinforced concrete members［J］.ACI Journal Proceedings，1965，62（10）：1237.

［2］ Gergely P，Lutz L A.Maximum crack width in reinforced concrete flexural members［J］.ACI Special Publication，1968，20：87.

［3］ Bazant Z P，Oh B H.Spacing of cracks in reinforced concrete［J］.Journal of Structural Engineering：ASCE，1983，109（9）：2066.

［4］ 丁大钧，黄德富，金芷生，等.钢筋混凝土构件刚度和裂缝的试验研究和对计算的建议［J］.土木工程学报，1985，18（4）：1.DING Dajun， HUANG Defu， JIN Zhisheng，etal.Experimental research on stiffness and crack width of RC members and proposals for the calculation［J］.China Civil Engineering Journal，1985，18（4）：1.

［5］ 赵国藩，李树瑶，廖婉卿.钢筋混凝土结构的裂缝控制［M］.北京：海洋出版社，1991 ZHAO Guofan，LI Shuyao，LIAO Wanqing.Crack control of reinforced concrete structures［M］.Beijing：China Ocean Press，1991.

［6］ 聂建国，沈聚敏.钢筋砼梁的斜裂缝宽度［J］.建筑结构，1994（6）：33.NIE Jianguo，SHEN Jumin.Diagonal crack width of reinforced concrete beam［J］.Building Structure，1994（6）：33.

［7］ Ju J W.On energy-based coupled elastoplastic damage theories：Constitutive modeling and computational aspects ［J］.International Journal of Solids Structures，1989，25（7）：803.

［8］ 李杰，任晓丹.混凝土静力与动力损伤本构模型研究进展述评［J］.力学进展，2010，40（3）：284.LI Jie，REN Xiaodan.A review on the constitutive model for static and dynamic damage of concrete［J］.Advances in Mechanics，2010，40（3）：284.

［9］ 李杰，吴建营.混凝土弹塑性损伤本构模型研究I：基本公式［J］.土木工程学报，2005，38（9）：14.LI Jie，WU Jianying.Elasto-plastic damage constitutive model for concrete based on damage energy release rates，Part I：Basic formulations［J］.China Civil Engineering Journal，2005，38（9）：14.

［10］ 中华人民共和国住房和城乡建设部.GB 50010—2010混凝土结构设计规范［S］.北京：中国建筑工业出版社，2011.Ministry of Housing and Urban-Rural Development of the People's Republic of China.GB50010—2010 Code for design of concrete structures［S］.Beijing：China Architecture &Building Press，2011.

［11］ LI Jie，REN Xiaodan.Stochastic damage model of concrete based on energy equivalent strain［J］.International Journal of Solids and Structures，2009，46（11／12）：2407.

［12］ Harries K A，Shahrooz B M，Soltani A.Flexural crack widths in concrete girders with high-strength reinforcement［J］.Journal of Bridge Engineering：ASCE，2012，17（5）：804.

［13］ 李娟.HRB级箍筋混凝土梁斜截面受力性能试验研究［D］.长沙：湖南大学，2007.LI Juan.Experimental study on mechanical behavior of diagonal section of reinforced concrete beams with HRB500 stirrups［D］.Changsha：Hunan University，2007.