高地震烈度下宽顶废石尾矿坝的动力响应分析

刘晓非，周汉民，崔 旋

（1.北京矿冶研究总院，北京100160；2.金属矿山智能开采技术北京市重点实验室，北京102628）

高地震烈度下宽顶废石尾矿坝的动力响应分析

刘晓非1，2，周汉民1，2，崔 旋1，2

（1.北京矿冶研究总院，北京100160；2.金属矿山智能开采技术北京市重点实验室，北京102628）

云南某尾矿库设计将排土场修整后作为尾矿坝，形成的宽顶废石坝最大坝高182 m，坝顶宽度496 m，尾矿坝处于8度地震烈度区。采用等效线性黏—弹性模型，对宽顶废石尾矿坝的动力响应进行分析，得出高地震烈度条件下坝体加速度、动应力及动力稳定性。研究结果对高地震烈度区尾矿坝工程建设具有指导意义。

高地震烈度；尾矿坝；排土场；动力响应

尾矿库是指筑坝拦截谷口或围地构成的用以贮存金属非金属矿山进行矿石选别后排出尾矿的场所［1］。目前，世界上正在使用的各类尾矿库超过2万座［2］。尾矿库作为具有高势能的巨大危险源，其一旦溃坝，将造成大量人员伤亡，有毒污染物泄露还将严重威胁环境安全。

在尾矿坝的失事类型中，地震破坏是主要原因之一。历史上由地震液化引起的尾矿坝溃坝有La Patagua尾矿坝、Los Maquis尾矿坝等［3］。我国2008年略阳县7座尾矿坝受损严重［4］。因此尾矿坝的动力稳定性一直是研究人员关心的重点问题。Hancock等［5］分析了尾矿坝震害并介绍了一种尾矿坝地震评价方法。周洋洋［6］结合实际工程，对者拉母箐尾矿坝进行地震动力响应分析，分析了坝体的位移、孔压的分布规律。徐志英等［7］用有限元法分析了德兴铜矿4号尾矿坝在9度地震时的液化情况和地震稳定性。

位于云南的某尾矿库，地处8度地震烈度区，其抗震问题成为必须解决的首要问题。结合当地条件及抗震需要，其坝型设计为宽顶废石坝，这种坝型的抗震稳定性是其能否安全实施的重要因素，对此深入研究将对指导高地震烈度区的尾矿库建设具有重要意义。本文通过动力响应计算，分析了该宽顶废石尾矿坝的加速度、应力及动力稳定性，研究结果可以为相似工程提供参考。

1 工程概况

云南某尾矿库位于平面呈“丫”字型的箐内，发育南、北两条冲沟，均对尾矿库没有大的影响。堆积坝位置以沉积岩为主，库区以火成岩为主。

此尾矿库的特点是建在已有排土场的上游，利用该矿山已产出和正在产出的大量废石筑坝，其初期坝利用该山沟已接近合拢的废石堆，加以修整，增设边坡马道、排水沟等，后期采用采场废石分期筑坝，建设为排土场与尾矿库共建型式，坝顶宽度500 m。宽顶废石坝形成的尾矿库库型条件好，可以解决尾砂粒级较细带来的筑坝困难问题。

宽顶废石尾矿坝设计最大坝高为182.00m，设计等级为二等库，防洪标准为500～1 000年一遇洪水标准，坝址设计烈度为8度。50年超越概率为5%的场地基岩峰值加速度为0.249g。坝体主剖面图如图1所示。

图1 尾矿坝主剖面图Fig.1 Main profile of the tailings dam

2 计算模型及参数

2.1 计算原理

尾矿坝的地震动力响应分析方法基于本构模型可分为基于等价黏弹性模型的等价线性分析方法、基于（黏）弹塑性模型的真非线性分析方法两类。等价黏弹性模型概念明确，应用方便，补充一些相关的计算模式后能够全面分析地震反应，而且在参数的确定和应用方面积累了较丰富的试验资料和工程经验，能为工程界所接受，实用性强，在尾矿坝地震反应分析中应用较广。

动力有限元的控制方程如下：

式中：［M］、［c］、［K］—整体质量矩阵、整体阻尼矩阵、整体刚度矩阵；—坝体结点加速度、速度、位移列阵；—输入地震加速度列阵。

动力计算时，首次迭代采用静力计算结果，根据各单元的剪应变γ1由试验资料计算出相应的剪切模量和阻尼比，按线性分析方法求解运动方程。其中阻尼采用Rayleigh假定，在计算中合成质量矩阵、刚度矩阵和阻尼矩阵。

这样就求解出了某个地震时段中坝体各单元的剪应变时程，由于该值是不断变化的，无法与γ1进行比较，为此假定一个等价的、不变的剪应变γeq来代替变化的时程，一般取：

式中：0.65为转换系数，带有一定的经验性，一般都在0.55～0.75；γmax—单元剪应变时程中的最大值。

然后将各单元计算的等价剪应变γeq同原来假定的γ1的数值相比较，若相差较大，则进行第二次迭代。第二次迭代即是用第一次迭代求得的等价剪应变γeq按照动本构模型重新求得剪切模量和阻尼比，再进行计算，直至算得各单元的等价剪应变值与假定剪应变值相差足够小，或达到预先规定的迭代次数为止。

2.2 计算模型

本文的三维计算模型中X轴取为顺河向，向上游为正；Y轴取为横河（坝轴）向，向右岸为正；Z轴取为竖直向，向上为正。模型的具体边界范围为：上、下游边界水平距离2 200m，横河（坝轴）向水平距离1 500m，底面边界距地表铅直距离为100～470m。坝体、坝基均采用四结点四面体单元。坝体网格见图2、3，整个计算模型共154 218个单元，35 258个节点。考虑最不利状况，动力计算时不激活尾矿砂单元。

该尾矿库工程场地地震安全性评价报告中指出，坝址处两个断层属早第四纪活动断裂，活动迹象不明显，因此计算不考虑断层对尾矿坝的影响。

2.3 计算参数

计算中涉及到的材料有坝体碎石料、坝基黏土及尾矿砂，材料参数通过室内动三轴试验得出。最大动剪模量Gdmax与有效固结应力σm′的关系可用式（3）表示。

式中：pa—大气压力；σ′m—平均有效固结应力，σ′m＝（σ1＋2σ3）/3；k—直线在纵轴上的截距，试验常数；n—直线的斜率，试验常数。

根据试验得到不同固结应力下最大动剪模量Gdmax—σ′m关系线，整理出的试验常数k、n值见表1。

图2 模型整体三维网格图（包括尾矿砂）Fig.2 3Dgrid graph of the whole model（including tailings）

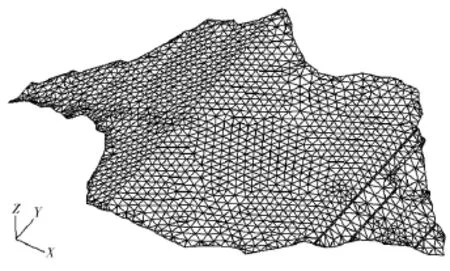
图3 尾矿坝三维网格图（不包括坝基）Fig.3 3Dgrid graph of the tailings dam（excluding dam foundation）

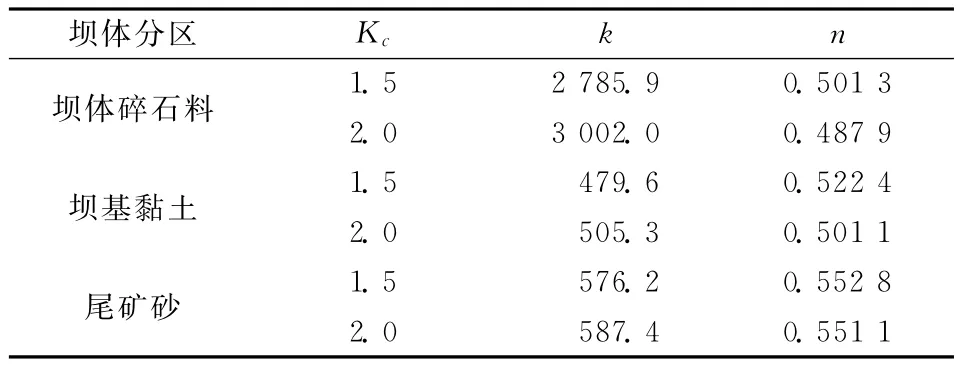
表1 动剪模量系数k与指数nTable 1 Dynamic shear modulus coefficientkand indexn

通过试验测得动剪切模量比Gd/Gdmax与动剪应变γd，以及动阻尼比λd与动剪应变γd的关系曲线如图4至图6。动力计算时输入相应关系曲线的控制数据，根据应力应变值进行内插和外延取值，用于计算。

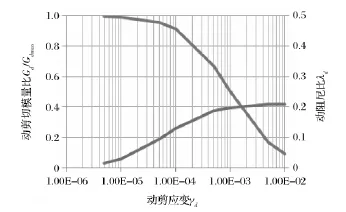
图4 坝体碎石料Gd/Gdmax和λd—γd关系曲线Fig.4 Curve ofGd/Gdmaxandλd—γdabout gravel in dam material

图5 坝基黏土Gd/Gdmax和λd—γd关系曲线Fig.5 Curve ofGd/Gdmaxandλd—γdabout clay in dam foundation

图6 尾矿砂Gd/Gdmax和λd—γd关系曲线Fig.6 Curve ofGd/Gdmaxandλd—γdabout tailings

2.4 地震时程曲线

本文采用固定边界，输入场地波（超越概率：50年5%）进行计算。计算的尾矿坝按非壅水建筑物考虑，《水工建筑物抗震设计规范》规定，非壅水建筑物地震加速度按50a超越概率5%取值。根据该工程场地地震安全性评价报告，坝址处50年超越概率5%的地震动峰值加速度值为0.249g，地震动反应谱特征周期0.50s；竖向加速度分量取水平向加速度分量的2/3。计算用地震持续时间为20s，时间间隔为0.02s，水平向和竖直向加速度的峰值分别为2.44m/s2、1.63m/s2。

图7 50年5%（设计地震）场地波加速度过程线Fig.7 Acceleration process line of site earthquake wave considering the exceeding probability to be 5%in the future 50years（design earthquake）

3 地震动力响应

选取坝体最大横剖面及纵剖面进行加速度、动应力及坝体动力稳定性分析，以下为计算结果。

3.1 坝体加速度

坝体水平向及竖直向加速度最大值和放大倍数如表2所示。在场地波作用下，坝体最大断面水平向、竖直向的最大绝对加速度如图8至图9所示。

表2 坝体加速度成果表Table 2 Result of dam acceleration

水平向最大加速度发生在坝顶，数值为4.0m/s2，放大倍数为1.61。竖直向最大加速度发生在坝顶，数值为3.1m/s2，放大倍数为1.87。由此可见：1）坝顶及坝顶附近坝坡区域的加速度反应相对较大，可采用坝顶及附近坡面加筋等抗震加固措施；2）由于坝体顶宽大，与常规土石坝坝顶一般20～30m有较大不同，坝体动力响应不大，无明显的鞭梢效应。

3.2 坝体动应力

坝体动拉应力最大值与该位置的静应力叠加后的结果见表3。最大动拉应力与静应力叠加后的拉应力极值等值线分别如图10至图11所示（单位MPa）。计算结果表明，地震波作用下的动拉应力最大值与静应力叠加后，在水平向坝体几乎全部受压，仅在下游坝坡有少许拉应力存在；在竖直向无拉应力出现。

图8 横剖面最大加速度等值线Fig.8 The maximum acceleration isoline in cross profile（a）downstream direction（b）transverse direction（c）vertical direction（unit：m/s2）

3.3 坝体动力稳定性

3.3.1 计算方法

在采用有限元静动力计算得到的坝体静应力和地震作用下每一瞬时动应力的基础上，可利用其成果采用如下方法分析坝坡的稳定性。

图9 纵剖面最大加速度等值线Fig.9 The maximum acceleration isoline in longitudinal profile（a）downstream direction（b）transverse direction（c）vertical direction（unit：m/s2）

表3 坝体动拉应力最大值与静应力叠加后拉应力极值（单位：MPa）Table 3 Tensile stress extreme value when max dynamic tensile stress stacked with static stress

图10 横剖面最大动拉应力与静应力叠加等值线Fig.10The isoline of max dynamic tensile stress superimposed with static stress in cross profile（a）downstream direction；（b）transverse direction；（c）vertical direction

图11 纵剖面最大动拉应力与静应力叠加等值线Fig.11 The isoline of max dynamic tensile stress superimposed with static stress in longitudinal profile（a）downstream direction；（b）transverse direction；（c）vertical direction

作用于单元滑动面上的法向应力σN和切向应力τN计算公式分别见式（4）和（5）。

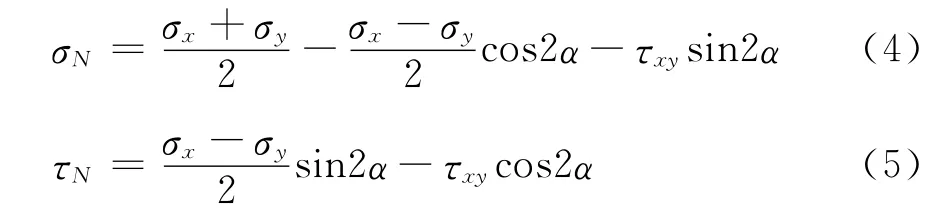
用有限元法分别计算出坝体的静动应力后，可在地震中的每一时刻对坝体进行动力稳定计算，其安全系数为：

式中：ci、φi—第i单元土体的凝聚力和内摩擦角；li—第i单元滑弧面的长度；σi、τi—第i单元滑弧面上法向应力和切向应力（静应力和动应力的叠加值）。

3.3.2 计算结果

在50年5%（设计地震）地震作用下，下游坝坡抗滑稳定最小安全系数时程曲线如图12，场地波整个过程中下游坝坡的最小安全系数为1.08，大于1.0，可见下游坝坡在地震过程中是稳定的。即在设计地震作用下，由滑弧稳定性分析得到的下游坝坡抗滑稳定性能满足要求。最小安全系数滑弧如图13所示。

图12 50年5%设计地震下下游坝坡抗滑稳定最小安全系数时程曲线Fig.12 Time-history curve of minimum anti-slide safety coefficient of downstream dam slope considering the exceeding probability to be 5%in the future 50years（design earthquake）

图13 最小安全系数滑弧位置示意图Fig.13 The schematic diagram of slip location with minimum safety factor

4 结论

1）本文讨论的宽顶废石尾矿坝，水平及竖直向加速度最大值均位于坝顶，但由于顶宽大，远超过常规土石坝，因此在设计地震作用下动力响应小，无明显的鞭梢效应。

2）场地地震波作用下，水平及竖直向上，坝体几乎全部以受压为主，两岸坝肩位置不会出现横缝。

3）设计地震作用下，下游坝坡抗滑稳定性能满足要求。但高尾矿坝在强地震作用下，坝顶附近一定范围内坝坡面堆石滚落易破坏下游坝坡，因此坝顶附近下游坝坡的护坡工作不可忽视。

4）采取适当有效的抗震措施，此宽顶废石尾矿坝可以抵御设计地震荷载的考验。

［1］于广明，宋传旺，潘永战，等.尾矿坝安全研究的国外新进展及我国的现状和发展态势［J］.岩石力学与工程学报，2014，33（增刊1）：3238-3248.

［2］Rico M，Benito G，Salgueiro A R.Reported tailings dam failures：a review of the European incidents in the worldwide context［J］.Journal of Hazardous Materials，2008，152（2）：846-852.

［3］张力霆.尾矿库溃坝研究综述［J］.水利学报，2013，44（5）：594-600.

［4］王飞跃.基于不确定性理论的尾矿坝稳定性分析及综合评价研究［D］.长沙：中南大学，2008.

［5］Hancock G R，Willgoose G R.An experimental and computer simulation study of erosion on a mine tailings dam wall［J］.Earth Surface Processes and Landforms，2004，29（4）：457-475.

［6］周洋洋，费维水，刘文连，等.地震作用下者拉母箐尾矿坝稳定性分析［J］.科学技术与工程，2010，10（11）：1671-1815.

［7］徐志英，沈珠江.地震液化的有效应力二维动力分析方法［J］.华东水利学院学报，1981（3）：57-62.

Dynamic response analysis of wide top waste rock tailings dam under high seismic intensity

LIU Xiaofei1，2，ZHOU Hanmin1，2，CUI Xuan1，2
（1.Beijing General Research Institute of Mining ＆Metallurgy，Beijing 100160，China；2.Beijing Key Laboratory of Nonferrous Intelligent Mining Technology，Beijing 102628，China）

A waste dump in Yunnan was designed to be a tailings dam which formed a wide top waste rock dam with maximum height of 182 m and 496 m crest width.The tailings dam is located in 8 degree seismic intensity zone.The dynamic response of wide top waste rock tailings dam under high seismic intensity is analyzed by using the equivalent linear viscosity-elasticity model.The acceleration，dynamic stress and dynamic stability of dam body are calculated.The results of the study have a guiding significance for the construction of tailings dam in high seismic intensity area.

high seismic intensity；tailings dam；waste dump；dynamic response

TD854＋.6

Α

1671-4172（2015）06-0093-06

刘晓非（1984-），女，工程师，硕士，水文地质专业，主要从事矿山尾矿库及排土场等方面的设计、研究工作。

10.3969/j.issn.1671-4172.2015.06.020