K-means 算法的分析及改进①
2015-04-14余晓平左文英
陈 敏,余晓平*,左文英
(1.石河子大学信息科学与技术学院,新疆 石河子832000;2.上海石化工业学校,上海201512)
0 引 言
随着人们对数据挖掘的深入研究和算法的应用过程中,人们发现针对不同的应用范围和领域需要的算法不同,某些算法可能在某些数据的可行性、效率、精度或简单性上具有一定的优势,但当数据类型转变或者应用领域不同,可能这种算法就不一定有优势了.所以,在使用算法之前我们需要对算法的优缺点和应用领域有一定了解,根据具体的情况选取合适的算法进行数据挖掘.
1 K-means 的算法分析
K-means 算法是数据挖掘技术中一种经典的基于划分的聚类算法,由于该算法的理论严谨、算法简单,并且收敛速度快而被广泛使用[1].Kmeans 算法采用的是迭代更新的思想,首先在数据集合中随机地选择k 个对象作为初始点来代表聚类或簇的中心,然后再根据"就近原则"对剩余的每个对象与各个簇的中心的距离将它重新赋给最近的簇,分配完毕后,重新计算每个簇的中心作为下一次迭代的聚类中心,再次进行所有对象的分配,不断重复这个计算簇中心后分配各对象的过程直到各聚类中心不再变化时终止[2].迭代使得选取的聚类中心越来越接近真实的簇中心,所以聚类效果越来越好,最后把所有对象划分为k 个簇.
K-means 算法的具体步骤[3]:
输出:k 个簇{s1,s2,…,sk}目标函数最小.
(1)聚类个数k;
(2)从数据集中随机选定k 个对象作为初始聚类中心c1,c2,…,ck;
(3)逐个将对象xi(i=l,2,...,n)按欧式距离分配给距离最近的一个聚类中心cj,1 <j <k

其中m 是数据属性的个数;
(4)计算各个聚类新的中心Cj
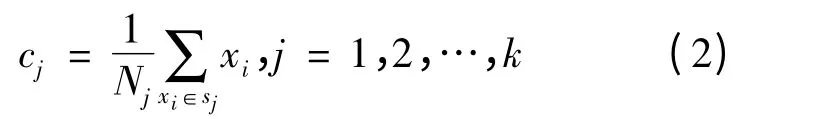
其中Nj是第j 个聚类sj中所包含的对象个数.
《中等职业学校语文教学大纲》中提出语文课程的目标是掌握日常生活和职业岗位需要的语文能力。这种能力是指能适应生活需要的、整合的、具有可持续发展前景的能力。要培养这种能力,必须将教育与生活紧密相连。因此在课堂教学中应将教学活动置于现实的生活背景之中,从而激发学生作为生活主体参与活动的强烈愿望,同时将教学的目的要求转化为学生作为生活主体的内在需要,让他们在生活中学习,在学习中更好地生活,从而获得有活力的知识,并使情操得到真正的陶冶。
(5)如果聚类中心不再变化,目标函数最小,算法终止,否则转步骤3.
K-means 算法的流程图如图1 所示.
2 改进的K-means 聚类算法
改进的K-means 主要能够根据对象间的相异度,基于欧氏距离度量的方法得出较为合适的聚类参数K 值.改进后算法的具体流程如图2 所示.
算法的开始需要从数据集合中选出距离最远的两个数据对象,传统的算法需要比较两两之间的距离,效率较为低下,针对这些不足,本文给出了另一种计算方法,首先计算出数据集中所有的边界点,即对于每一维来说找出最大值和最小值,然后找到数据集中所对应的每一个数据点,相对于数据量大的数据集来说,边界点的数量会显得少很多,如此以来数据的处理量会大量的减少.步骤实施过程的详细描述如下:
(1)针对一个数据集Sn= {X1,X2,X3,…,Xn},其中包含了n 个数据对象,首先从数据集Sn中找出所有边界点,组成一个小的数据集,再从边界点的数据集中找出距离最远的两个点作为初始的聚类中心,即C1和C2.
(2)将数据集中的每一个对象Xi分别计算出到上述两个初始聚类中心的欧式距离di,根据就近原则,即为Xi到聚类中心距离值小的点Min(di),将给数据点划分为该聚类中心,从而将所有的数据点划分成为以C1和C2为中心的两大类.同时,在将所有节点分配到各个簇中心节点时,如果出现某一个簇心只有它自身一个节点,则将该节点列入孤立点,不作为簇中心出现.

图1 K-means 算法的流程图
(3)计算出以上两大类中所有数据点距离中心点的最大距离,即为Max(di),同时查找出该数据点Xj.
(4)检验该数据点Xj能否成为下一个聚类中心点C3.如果可以则转入步骤2 中继续聚类,然后找下一个聚类中心点C4,C5…等,一直到找不出满足条件的中心点为止,否则,得出该数据集Sn的聚类个数K 值.
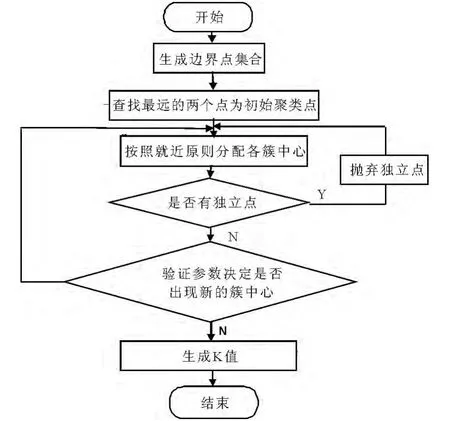
图2 改进K-means 算法的基本流程
这里需要重点分析的是距离已有中心点距离最远的一个点Xj成为聚类中心点的判定,如果Xj到其所在中心的距离为dj,且dj得值为各个聚类中心点平均距离的大于等于0.5[4],并且小于1,文献中参数的经验值一般取为0.5,则该点Xj可独立成为一个中心聚点.避免了将距离某一个已有的聚类中心比较临近而离其它聚类中心都远的点作为侯选对象的可能.因此,采用该算法可以保证每次取到的新的聚类中心离已有的聚类中心的距离都比较远.而且该算法不需要预先给出聚类个数,它可以根据一定的计算规则自动地确定初始聚类中心的个数.该算法的伪代码如下:


3 改进算法与K-means 算法性能对比
为了评价改进后的K-means 算法与Kmeans 算法的优良,采用了IRIS 数据集作为测试数据,通过大量的聚类算法实验已经证明,IRIS 数据集对测试聚类算法中的K-means 算法有很好的验证效果,所以该数据集经常被用作检验聚类算法的性能的标准数据.IRIS 数据集即为鸢尾花数据集,该数据集可以从加州大学厄文分校的(UCI)的机器学习库中得到.鸢尾花数据集包含150 种鸢尾花的信息,每50 种取自三个鸢尾花种之一:Setosa、Versicolour 和Virginica.每个花的特征用下面5 种属性描述:萼片长度(厘米)、萼片宽度(厘米)、花瓣长度(厘米)、花瓣宽度(厘米)和类(Setosa,Versicolour,Virginica),在这些样本中的Setosa 样本与其它两类间是完全分离,而在Versicolor 样本和Virginica 样本间有部分的数据交叉.
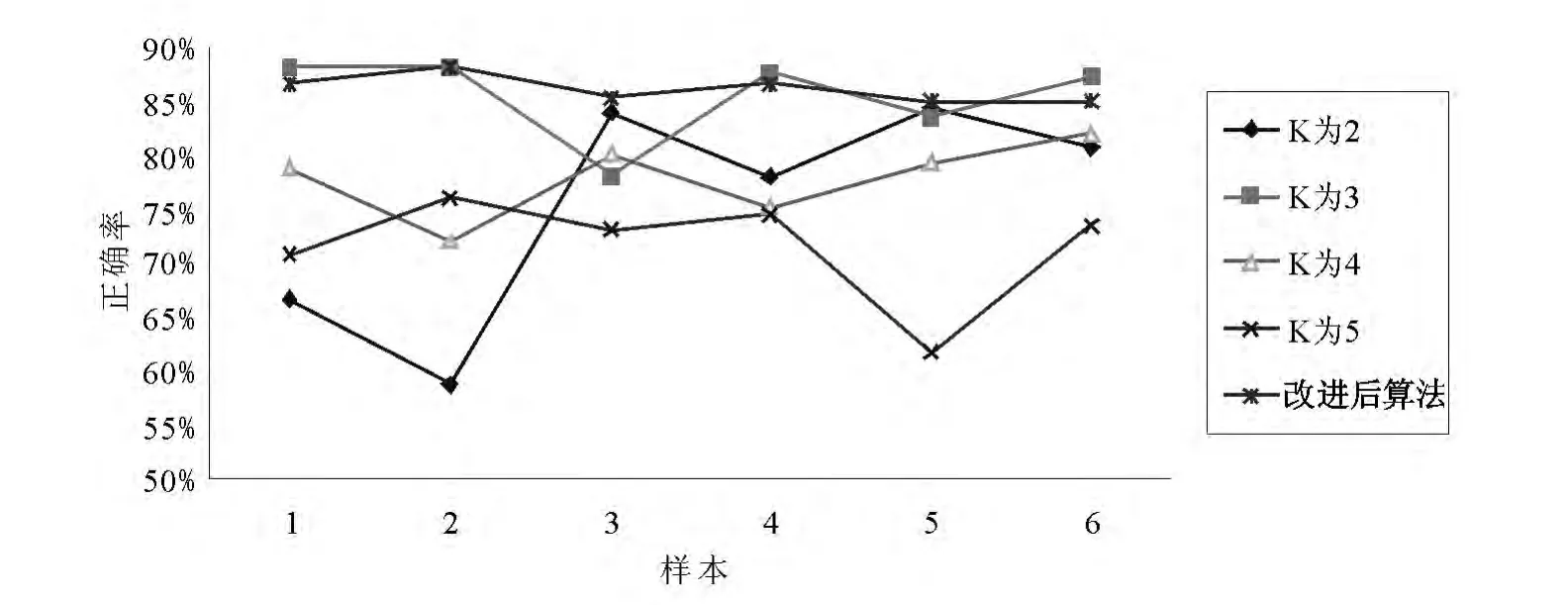
图3 改进前后算法正确率比较图

图4 K-means 聚类正确率分布图
IRIS 数据集共有5 个属性集和150 个样本数据,一方面在属性方面既不至于过于繁琐,另一方面又保证了一定的数据量和代表性,并且Hathaway(1995)给出的IRIS 数据的每一类的实际类中心位置:Setosa 类为(5.00,3.42,1.46,0.24),Versicolour 类为(5.93,2.77,4.26,1.32)和Virginica 类为(6.58,2.97,5.55,2.02),有了这些明确的数据对我们测试新算法进行参数的比对很有帮助.实验结果和对比分析
(1)聚类个数的比较
由于IRIS 数据集每50 个对象为一类,所以在取样本集时考虑到每一类均衡将实验数据集划分为6 次样本集,样本集1 为IRIS 数据集中序号为偶数的数据共75 条,样本集2 为IRIS 数据集中序号为奇数的数据共75 条,样本集3 为IRIS 数据集中序号不能整除3 后数据共100 条,样本集4 为IRIS 数据集中删除序号不能整除4 的数据共113条,样本集5 为IRIS 数据集中序号不能整除5 的数据共120 条,样本集6 为IRIS 数据集共150 条.这6 个样本集覆盖了数据集中的所有数据,实验过程中分别用K-means 算法和改进后算法进行了实验.
经典的K-means 算法需要事先用户指定好聚类个参数K 值,根据用户指定的K 参数可以得到不同的聚类,这里根据聚类的经验对IRIS 数据集进行K 值的设定,测试聚类分别将聚类K 值设定为2、3、4 和5,然后通过对6 个样本执行不同的K 值后,聚类后的Setosa、Versicolour 和Virginica 三类的正确率各不相同,算法的执行聚类结果如表1所示:

表1 改进后K-means 聚类结果
通过以上的样本测试,正确率因聚类K 值不同而不同,通过求平均值得出以下每个K 值对应的平均正确率如表2 所示.由此可以看出,当K 取值为3 时正确率为最高,所以在K-means 算法过程中如何确定合适的K 值对于用户来说是一个较为难解决的问题.

表2 K-means 算法平均正确率表
这里对改进后的K-means 算法也进行同一个数据集的测试,由于改进后的算法是由程序自动生成合适的K 值,所以这里不需要进行输入,并且当程序首先找出边界点时,得到共有14 条记录属于边界点内,这样效率远远高于求150 个数据对象之间的距离.改进后的K-means 算法在运行时验证参数值的范围介于0.45 与0.55 之间,6 个样本的程序结果均显示自动生成了3 簇,而IRIS 数据集的最佳聚类结果也是3 簇,具体的结果如表1-3 所示,这首先保证了K 值与标准数据库的一致性,并且在6 个样本中首先对于Setosa 样本中的50 条记录能保证100%的正确率,对Versicolour 类的正确率也达到99%,Virginica 和Versicolour 类部分数据本身就有交叉,所以在Virginica 类的正确率低.

表3 改进聚类结果

样本1 25 0 100% 25 0 100% 15 10 60%样本2 25 0 100% 25 0 100% 16 9 64%样本3 33 0 100% 32 1 97% 20 14 59%3 样本4 37 0 100% 37 1 97% 24 14 63%样本5 40 0 100% 40 0 100% 22 18 55%样本6 50 0 100% 50 0 100% 28 22 56%
通过计算得到改进K-means 算法的平均正确率为86.17%,高于K-means 算法中最高的正确率83.67%.根据算法改进前后的正确率对比图3 ~7 我们能够很明显的看出,K-means 算法的正确率首先波动很大,样本结果出现正确率不稳定,最低的正确率是56%.因为当初始点的随机产生对聚类的结果影响很大,如果初始点随机都产生的距离很近或者在一个簇中,聚类的结果不仅迭代次数多,同时分类的结果也产生很大的差异.而改进后的算法正确率波动范围比较小.对于6 个样本正确率都相当,比对后得出改进后的算法不仅能自动得出生成合适的聚簇个数,同时聚类的正确率也高于经典的K-means 算法,如图3 所示.
(2)对于孤立点和噪声的比较
由于K-means 算法对于噪声和孤立点的数据很敏感,这些孤立点和噪声会对计算平均值产生巨大的影响,造成平均值有很大的偏离,所以在改进的K-means 算法中对孤立点和噪声进行了改造,当数据库扫描完毕后,如果聚簇结果中出现了孤立点,则将该数据点剔除后继续扫描库.这里为了检验两种算法对孤立点的敏感性,仍然使用原有的IRIS 数据集,在数据集中加入一条记录萼片长度、萼片宽度、花瓣长度和花瓣宽度均为15,K 值仍然为3.由于K-means 算法首先随机取K 个对象生成了簇中心,所以在测试时候为了结果准确且有一定代表性,反复调用K-means 算法10 次得到的结果正确率如图4 所示.
使用改进后的K-means 算法首先在数据集中找出最远的两个数据点,分别为第14 条记录(4.3,3,1.1,0.1)和第151 条记录(15,15,15,15),同时所有的记录产生两类,前150 条记录都以第14 条记录为中心的簇中,而第151 条记录单独成为一簇,这样程序将首先标记出第151 条记录,并且从IRIS 表中剔除,继续在重新聚类,结果的显示正确率为86.17%,高于K-means 算法中得到的72.79%的正确率,同时也能够判断出独立点.
4 小 结
通过以上的对比可发现,改进后的算法首先可以自动得出K 值,而不需要用户指定值,降低了用户的进行聚类的工作难度,同时对数据集中存在异常点能够判断读出后,不再进行聚类,这样不会对聚类的结果产生影响,对大量数据进行聚类过程中计算最远点之间距离采用先生成边界集合的方法,大大降低了程序运行的时间,提高了工作效率,因而可以说改进后的算法应用效果要优于K-means算法.
[1] FAHIM A.M,SALEM A.M,TORKEY F.A.An efficient enhanced k-means clustering algorithm[J].2006,7(10),22-24.
[2] 张雪凤,张桂珍,刘鹏.基于聚类准则函数的改进K-means算法[J].计算机工程与应用,2011,11:123-127.
[3] 张靖,段富.优化初始聚类中心的改进k-means 算法[J].计算机工程与设计,2013,05:1691-1694+1699.
[4] 毛韶阳,林肯立.优化k-means 初始聚类中心研究[J].计算机工程与应用,2007,43(22):179-181.
