对称性在积分计算中的应用①
2015-04-14曹万昌汪宏远张志旭温绍泉崔成贤
曹万昌,汪宏远,张志旭,温绍泉,崔成贤
(佳木斯大学理学院,黑龙江 佳木斯154007)
0 引 言
积分是高等数学非常重要的内容,在积分计算中常会遇到积分区域和被积函数具有某种对称性的题型,在计算中恰当利用对称性可以简化积分求解过程,或不必计算就可得到结果,因此,通过对此类题进行解析,供大家参考.
1 相关的定理

注意:这里闭区间[-a,a]也可换成(-a,a)或(-∞,+∞)公式还成立.
定理2 (1)设有界闭区域D=D1∪D2,D1与D2关于y 轴对称.设函数f(x,y)在有界闭区域D 上连续,那么
若f(x,y)是关于x 的奇函数,即f(-x,y)=-f(x,y)则
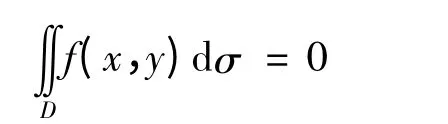
若f(x,y)是关于x 的偶函数,即f(-x,y)=f(x,y)则

(2)设有界闭区域D=D1∪D2,D1与D2关于x 轴对称.设函数f(x,y)在有界闭区域D 上连续,那么
若f(x,y)是关于y 的奇函数,即f(x,-y)=-f(x,y)则
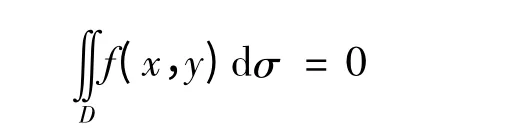
若f(x,y)是关于y 的偶函数,即f(x,-y)=f(x,y)则

定理3 设有界闭区域D 关于x 轴和y 轴均对称,函数f(x,y)在D 上连续且f(x,y)关x 和y 均为偶函数,则

其中D3是D 的第一象限的部分:
D3={(x,y)∈D|x ≥0,y ≥0}
定理4 设有界闭区域D 关于原点对称,函数f(x,y)在D 上连续,如果f(-x,-y)=-f(x,y),则如果f(-x,-y)=f(x,y),其中D1={(x,y)∈D|x ≥0},D2={(x,y)∈D|y ≥0}
定理5 设空间有界闭区域Ω=Ω1∪Ω2,Ω1与Ω2关于xoy 坐标面对称,函数f(x,y,z)在Ω上连续,那么:
若f(x,y,z)是关于z 的奇函数,则

若f(x,y,z)是关于z 的偶函数,则:

同时,若Ω 关于yoz 坐标面对称,f(x,y,z)关于奇函数或偶函数;或者若Ω 关于xoz 坐标面对称f(x,y,z)关于y 为奇函数或偶函数,同样也有类似结论.
2 定理的分析与应用
观察所求积分的特点,先看积分范围是否具有对称性,再看被积函数的是否具有奇偶性或能否变换成奇偶性函数和或差的形式,这里技巧性很强,通过几个实例来体会一下.
解: 被积函数是奇函数,积分区间(-1,1),由对称性得I=0
解: 这个积分在实数范围不能积分,需要改变思路,做下列变化.积分和积分只是变量形式不同,结果相同.变形为两个积分的乘积用二重积分做.所以I2=其中D={(x,y)∣x,y ∈R},积分区域关于x 轴和y 轴对称,被积函数为x 和y 的偶函数D1={(x,y)∣x ≥0,y ≥0}求得I2=π,即I=
例3 已知D={(x,y)|-x ≤a,x ≤y ≤a}.D1={(x,y)|0 ≤x ≤a,x ≤y ≤a}.则
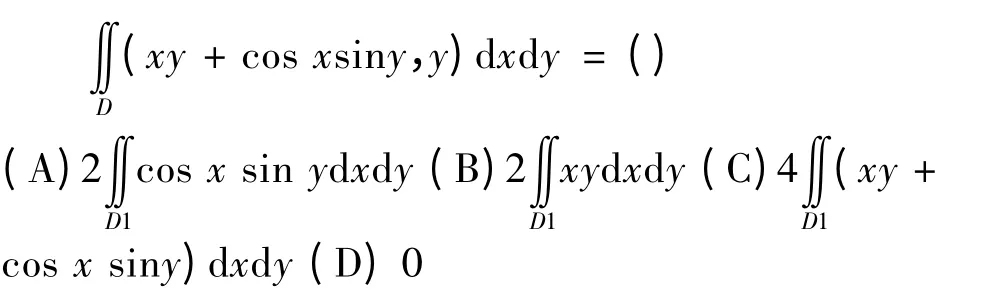
提示:将D 分成四个部分D1,D2,D3,D4
而cos x sin y 在D3 ∪D4 上关于y 的奇函数,在D1 ∪ D2 上关于 x 的偶函数.选(A).
解: 积分区域如图2,添加辅助线y=x 将D分为D1,D2 利用对称性.


图1

图2
例6 设Ω1由x2+y2+z2≤R2,z ≥0 确定,Ω2由x2+y2+z2≤R2,x ≥0,y ≥0,z ≥0 所确定则正确选项().

提示:利用对称性(A)(B)(D)左边为0,右边为正.显然不对,故选(C).
3 结 语
在定积分,重积分计算时必须兼顾积分区域和被积函数两方面,只有当两方面的对称性相匹配时才能使用.要善于发现利用问题中所具有的对称性,会起到事半功倍的效果.当然,发现对称性并巧妙利用有一定难度,重要的是要多实践,大胆创新,开拓思路,这样才能较好地掌握对称性在积分运算的应用.
[1] 同济大学应用数学系.高等数学[M].5 版.北京:高等教育出版社.2002.
[2] 常浩.对称性在积分中的应用[J].高等数学研究,2011,(3):59-63.
[3] 周海娜.对称性在积分计算中的应用[J].温州科技职业学院学报,2009,(6):46-48.
