从B(B0)空间到空间的算子Tμ，φ D 的有界性和紧性①

王艳永，商庆宝

(1.吕梁学院 数学系，山西 吕梁03300;2.文心高中，山东 莒县276500)

0 引 言

设D={z:|z|＜1}是复平面上的单位圆盘，H(D)表示D 上的全纯函数的全体.φ 是D →D 的一个解析映射，u 是D 上的一个解析函数，设μ(z)是正连续函数且有μ(z)=μ(|z|).

令

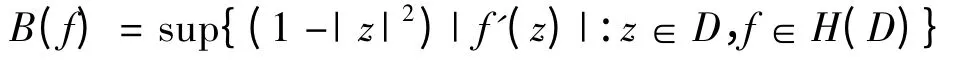
若B(f)＜∞，则称f 属于Bloch 空间B.

若

则称f 属于小Bloch 空间B0，B0是B 的闭子空间，B 空间以‖fB‖=|f(0)|+B(f)为范数成为Banach 空间.

令

其中μ(z)是正连续函数且μ(z)=μ(| z|).若‖f‖H∞μ＜∞，则称f 属于空间

Ohno 和赵如汉在文献［1］中研究了Bloch 空间和小Bloch 上加权复合算子的有界性和紧性问题，后来他们和Stroethoff 在文献［2］中将上述结果推广到α-Bloch 空间上.于燕燕，刘永民在文献［3］中讨论了在两种不同Bloch 型空间之间的有界性和紧性.于燕燕在［4］中讨论了从对数Bloch 空间到Bα空间Volterra 型复合算子.刘浩，商庆宝，王艳永在文献［5］中研究了加权Begman 空间到)空间的Volterra 复合算子的有界型和紧性.

本文研究算子

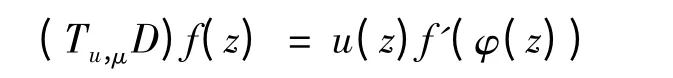
其中Cμ是复合算子，D 是微分算子.

本文得到了从B(B0)空间到空间的算子Tu，φ是有界算子和紧算子的充要条件.文中字母C是一个正常数，不同的地方可以不同.A ≅B 表示存在一个常数C，满足C-1A ≤B ≤CA.

1 主要引理与定理

下面的引理1.1 类似文献［6］的相应的引理，由Montel 原理可证，证明过程本文省略.

引理1.1 设u 是D 上的解析函数，φ 是D →D 的一个全纯自映射，μ 是正连续函.X 是空间B(B0)，Y 是空间，则算子Tu，φD:X →Y 是紧的充要条件是Tu，φD:X →Y 是有界的且对于任意有界序列(fk)k∈N在D 的紧支集上一致收敛于0，有

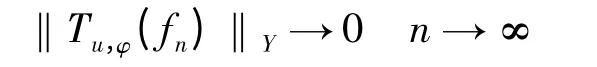
定理1.2 φ 是D →D 的一个解析映射，μ 是D上的解析函数，且是正连续函数，则以下三个条件等价:

(c)

定理1.3 μ 是D →D 的一个解析映射，μ 是D上的解析函数，且μ 是正连续函数，并且满足是有界算子，则以下三个条件等价:

(a):Tu，μD:B0→是紧算子;

(b):Tu，φD:B →是紧算子;

(c)

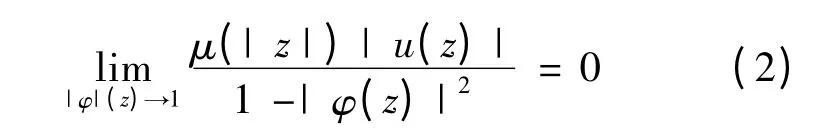
2 定理的证明

取

定理1.2 的证明(b)⇒(a)显然.

(a)⇒(c).设Tu，φD:B0→是有界算子.取f(z)=z ∈B0，则Tu，φDf=u ∈，有

有

则得

即有

另有

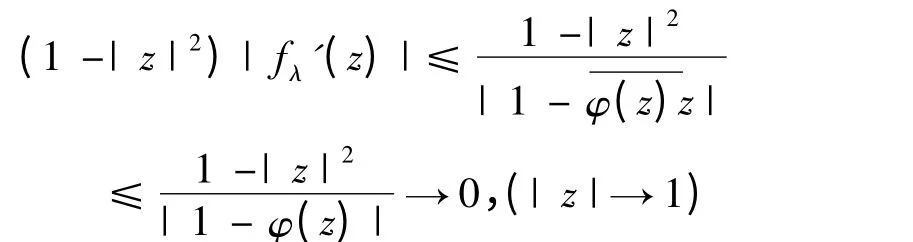
即fλ(z)∈B0，因此对于λ ∈D，有

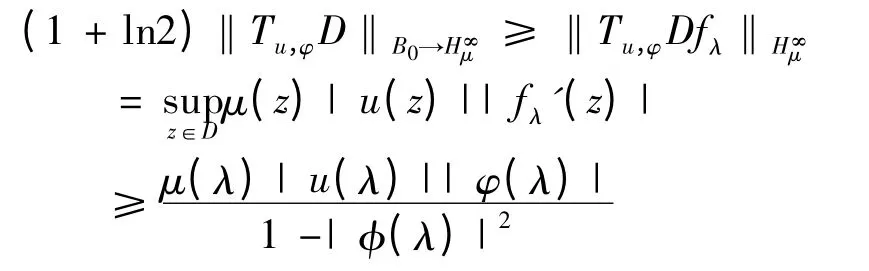
所以有

因此对于λ ∈D，取r ∈(0，1)，则

又由(2)式得

由上可知

即(1)成立.

(c)⇒(b).设(1)式成立，那么对任意的f(z)∈B，z ∈D，则Tu，μDf=u ∈H∞μ，有

则Tu，μD:B →是有界算子.证毕!

定理1.3 的证明(b)⇒(a)显然.

(a)⇒(c).设Tu，μD:B0→:是紧算子.取zm(m ∈N)，使取检验函数

有

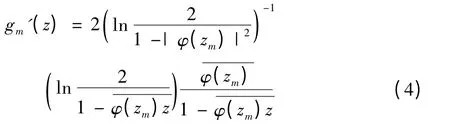
易得

由(4)式可得

而

由可知‖gm‖B≤ln2+C=M2(M2是不依赖于m 的常数).易知gm(z)∈H(¯D)，因此对任意的m ∈N，gm(z)∈B0.固定|z|=r ＜1，有

→0，(m →∞)

即是当m →∞时，gm在D 的紧子集上一致收敛 于 0， 因 此 由 (3)和 引 理 1.1 得

另有

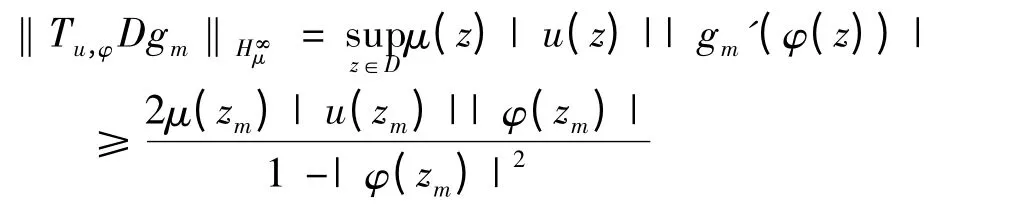
有上式知

即有

即(3)式成立.

(c)⇒(b).设(c)式成立，那么对任意的ε ＞0，存在r ∈(0，1)，当|φ(z)|＞r 时

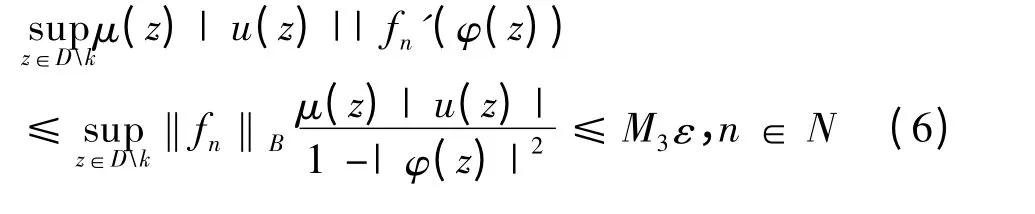
另有柯西估计知，fn′在D 的紧子集上一致收敛于0;则存在n0∈N，当n ≥n0时，有|fn′(φ(z))|＜ε，(z ∈K).有

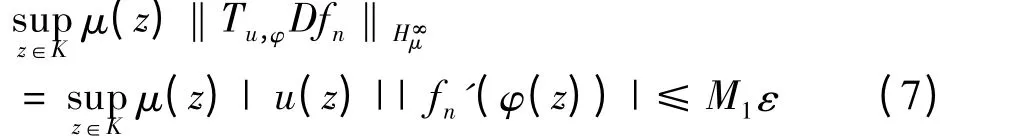
由(6)和(7)式知，当n ≥n0时，有

［1］ Ohno S，Zhao Ruhan Weighted Composition Operators on the Bloch Space［J］.Bull.Austal.Math.Soc.2001，63(2):177－185.

［2］ Ohno S，Stroethoff K and Zhao Ruhan Weighted Composition Operators between Bloch－type Spaces［J］.Rocky Mountain J.Math，2003，33(1):191－215.

［3］ Yu Yanyan Liu Yongmin On a Li－SteveIntegral Operators between Different Weighted Bloch－type Spaces［J］.Jornal of Inequalities and Applications.Vol.2008(2008).Article ID 780845，14pages.

［4］ 于燕燕，从对数Bloch 空间到空间Volterra 型复合算子［J］.徐州师范大学学报;自然科学版，2009，27(3)，14.

［5］ 刘浩，商庆宝，王艳永.从加权Bergman 空间到空间的Volterra 型复合算子的有界性和紧性［J］.徐州师范大学学报:自然科学版.2010，28(2):11－15.

［6］ Zhu K.H.Operator Theoty in Tunction Spaces［M］.Marcel Dekker，New York，1990.